Trending in Mathematics
 2602.16381
2602.16381Derivations as Algebras
Differential categories provide the categorical foundations for the algebraic approaches to differentiation. They have been successful in formalizing various important concepts related to differentiation, such as, in particular, derivations. In this paper, we show that the differential modality of a differential category lifts to a monad on the arrow category and, moreover, that the algebras of this monad are precisely derivations. Furthermore, in the presence of finite biproducts, the differential modality in fact lifts to a differential modality on the arrow category. In other words, the arrow category of a differential category is again a differential category. As a consequence, derivations also form a tangent category, and derivations on free algebras form a cartesian differential category.
2602.16381
Feb 2026Category Theory
HAL-MLE Log-Splines Density Estimation (Part I: Univariate)
We study nonparametric maximum likelihood estimation of probability densities under a total variation (TV) type penalty, sectional variation norm (also named as Hardy-Krause variation). TV regularization has a long history in regression and density estimation, including results on $L^2$ and KL divergence convergence rates. Here, we revisit this task using the Highly Adaptive Lasso (HAL) framework. We formulate a HAL-based maximum likelihood estimator (HAL-MLE) using the log-spline link function from \citet{kooperberg1992logspline}, and show that in the univariate setting the bounded sectional variation norm assumption underlying HAL coincides with the classical bounded TV assumption. This equivalence directly connects HAL-MLE to existing TV-penalized approaches such as local adaptive splines \citep{mammen1997locally}. We establish three new theoretical results: (i) the univariate HAL-MLE is asymptotically linear, (ii) it admits pointwise asymptotic normality, and (iii) it achieves uniform convergence at rate $n^{-(k+1)/(2k+3)}$ up to logarithmic factors for the smoothness order $k \geq 1$. These results extend existing results from \citet{van2017uniform}, which previously guaranteed only uniform consistency without rates when $k=0$. We will include the uniform convergence for general dimension $d$ in the follow-up work of this paper. The intention of this paper is to provide a unified framework for the TV-penalized density estimation methods, and to connect the HAL-MLE to the existing TV-penalized methods in the univariate case, despite that the general HAL-MLE is defined for multivariate cases.
2602.16259
Feb 2026Statistics Theory
Do More Predictions Improve Statistical Inference? Filtered Prediction-Powered Inference
Recent advances in artificial intelligence have enabled the generation of large-scale, low-cost predictions with increasingly high fidelity. As a result, the primary challenge in statistical inference has shifted from data scarcity to data reliability. Prediction-powered inference methods seek to exploit such predictions to improve efficiency when labeled data are limited. However, existing approaches implicitly adopt a use-all philosophy, under which incorporating more predictions is presumed to improve inference. When prediction quality is heterogeneous, this assumption can fail, and indiscriminate use of unlabeled data may dilute informative signals and degrade inferential accuracy. In this paper, we propose Filtered Prediction-Powered Inference (FPPI), a framework that selectively incorporates predictions by identifying a data-adaptive filtered region in which predictions are informative for inference. We show that this region can be consistently estimated under a margin condition, achieving fast rates of convergence. By restricting the prediction-powered correction to the estimated filtered region, FPPI adaptively mitigates the impact of biased or noisy predictions. We establish that FPPI attains strictly improved asymptotic efficiency compared with existing prediction-powered inference methods. Numerical studies and a real-data application to large language model evaluation demonstrate that FPPI substantially reduces reliance on expensive labels by selectively leveraging reliable predictions, yielding accurate inference even in the presence of heterogeneous prediction quality.
2602.10464
Feb 2026Statistics Theory
 2602.11747
2602.11747High-Probability Minimax Adaptive Estimation in Besov Spaces via Online-to-Batch
We study nonparametric regression over Besov spaces from noisy observations under sub-exponential noise, aiming to achieve minimax-optimal guarantees on the integrated squared error that hold with high probability and adapt to the unknown noise level. To this end, we propose a wavelet-based online learning algorithm that dynamically adjusts to the observed gradient noise by adaptively clipping it at an appropriate level, eliminating the need to tune parameters such as the noise variance or gradient bounds. As a by-product of our analysis, we derive high-probability adaptive regret bounds that scale with the $\ell_1$-norm of the competitor. Finally, in the batch statistical setting, we obtain adaptive and minimax-optimal estimation rates for Besov spaces via a refined online-to-batch conversion. This approach carefully exploits the structure of the squared loss in combination with self-normalized concentration inequalities.
2602.11747
Feb 2026Statistics Theory
 2602.03716
2602.03716Fel's Conjecture on Syzygies of Numerical Semigroups
Let $S=\langle d_1,\dots,d_m\rangle$ be a numerical semigroup and $k[S]$ its semigroup ring. The Hilbert numerator of $k[S]$ determines normalized alternating syzygy power sums $K_p(S)$ encoding alternating power sums of syzygy degrees. Fel conjectured an explicit formula for $K_p(S)$, for all $p\ge 0$, in terms of the gap power sums $G_r(S)=\sum_{g\notin S} g^r$ and universal symmetric polynomials $T_n$ evaluated at the generator power sums $σ_k=\sum_i d_i^k$ (and $δ_k=(σ_k-1)/2^k$). We prove Fel's conjecture via exponential generating functions and coefficient extraction, solating the universal identities for $T_n$ needed for the derivation. The argument is fully formalized in Lean/Mathlib, and was produced automatically by AxiomProver from a natural-language statement of the conjecture.
2602.03716
Feb 2026Combinatorics
The Riemann Hypothesis: Past, Present and a Letter Through Time
This paper, commissioned as a survey of the Riemann Hypothesis, provides a comprehensive overview of 165 years of mathematical approaches to this fundamental problem, while introducing a new perspective that emerged during its preparation. The paper begins with a detailed description of what we know about the Riemann zeta function and its zeros, followed by an extensive survey of mathematical theories developed in pursuit of RH -- from classical analytic approaches to modern geometric and physical methods. We also discuss several equivalent formulations of the hypothesis. Within this survey framework, we present an original contribution in the form of a "Letter to Riemann," using only mathematics available in his time. This letter reveals a method inspired by Riemann's own approach to the conformal mapping theorem: by extremizing a quadratic form (restriction of Weil's quadratic form in modern language), we obtain remarkable approximations to the zeros of zeta. Using only primes less than 13, this optimization procedure yields approximations to the first 50 zeros with accuracies ranging from $2.6 \times 10^{-55}$ to $10^{-3}$. Moreover we prove a general result that these approximating values lie exactly on the critical line. Following the letter, we explain the underlying mathematics in modern terms, including the description of a deep connection of the Weil quadratic form with the world of information theory. The final sections develop a geometric perspective using trace formulas, outlining a potential proof strategy based on establishing convergence of zeros from finite to infinite Euler products. While completing the commissioned survey, these new results suggest a promising direction for future research on Riemann's conjecture.
2602.04022
Feb 2026Number Theory
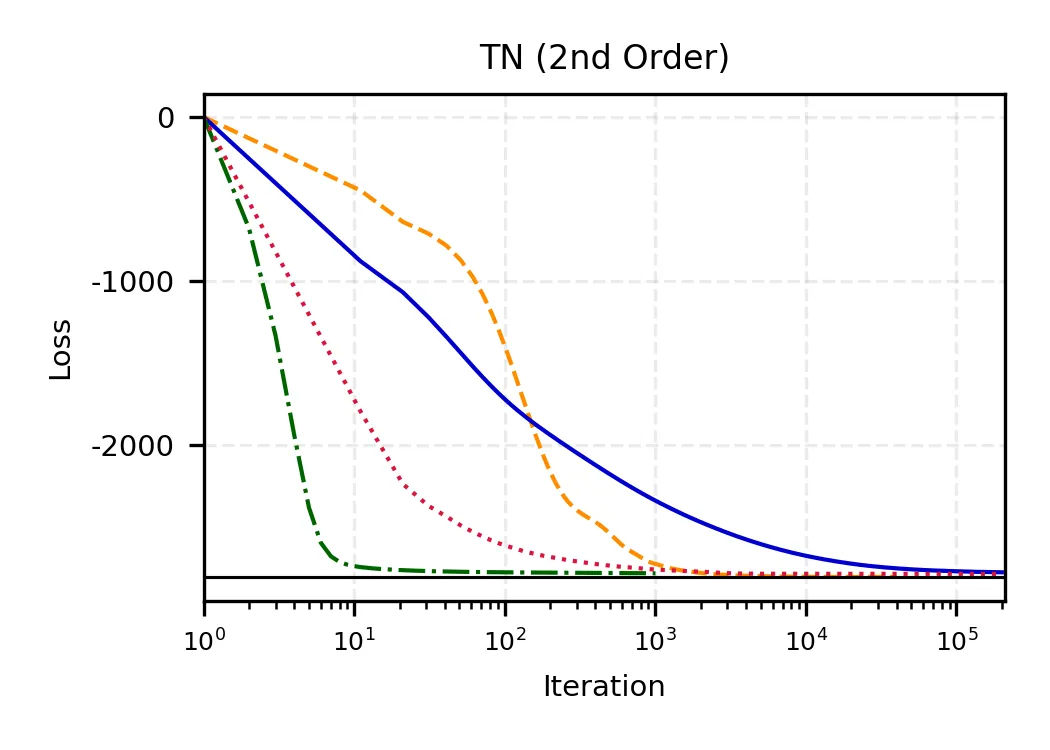
Introduction to optimization methods for training SciML models
Optimization is central to both modern machine learning (ML) and scientific machine learning (SciML), yet the structure of the underlying optimization problems differs substantially across these domains. Classical ML typically relies on stochastic, sample-separable objectives that favor first-order and adaptive gradient methods. In contrast, SciML often involves physics-informed or operator-constrained formulations in which differential operators induce global coupling, stiffness, and strong anisotropy in the loss landscape. As a result, optimization behavior in SciML is governed by the spectral properties of the underlying physical models rather than by data statistics, frequently limiting the effectiveness of standard stochastic methods and motivating deterministic or curvature-aware approaches. This document provides a unified introduction to optimization methods in ML and SciML, emphasizing how problem structure shapes algorithmic choices. We review first- and second-order optimization techniques in both deterministic and stochastic settings, discuss their adaptation to physics-constrained and data-driven SciML models, and illustrate practical strategies through tutorial examples, while highlighting open research directions at the interface of scientific computing and scientific machine learning.
2601.10222
Jan 2026Numerical Analysis
 2601.07222
2601.07222The motivic class of the space of genus $0$ maps to the flag variety
Let $\operatorname{Fl}_{n+1}$ be the variety of complete flags in $\mathbb{A}^{n+1}$ and let $Ω^{2}_β(\operatorname{Fl}_{n+1})$ be the space of based maps $f:\mathbb{P}^{1}\to \operatorname{Fl}_{n+1}$ in the class $f_{*}[\mathbb{P}^{1}]=β$. We show that under a mild positivity condition on $β$, the class of $Ω^{2}_β(\operatorname{Fl}_{n+1})$ in $K_{0}(\operatorname{Var})$, the Grothendieck group of varieties, is given by \[ [Ω^{2}_β(\operatorname{Fl}_{n+1})] = [\operatorname{GL}_{n}\times \mathbb{A}^{a}]. \] The proof of this result was obtained in conjunction with Google Gemini and related tools. We briefly discuss this research interaction, which may be of independent interest. However, the treatment in this paper is entirely human-authored (aside from excerpts in an appendix which are clearly marked as such).
2601.07222
Jan 2026Algebraic Geometry
 2601.07421
2601.07421Resolution of Erdős Problem #728: a writeup of Aristotle's Lean proof
We provide a writeup of a resolution of Erdős Problem #728; this is the first Erdos problem (a problem proposed by Paul Erdős which has been collected in the Erdos Problems website) regarded as fully resolved autonomously by an AI system. The system in question is a combination of GPT-5.2 Pro by OpenAI and Aristotle by Harmonic, operated by Kevin Barreto. The final result of the system is a formal proof written in Lean, which we translate to informal mathematics in the present writeup for wider accessibility. The proved result is as follows. We show a logarithmic-gap phenomenon regarding factorial divisibility: For any constants $0<C_1<C_2$ there exist infinitely many triples $(a,b,n)\in\mathbb N^3$ such that \[ a!\,b!\mid n!\,(a+b-n)!\qquad\text{and}\qquad C_1\log n < a+b-n < C_2\log n. \] The argument reduces this to a binomial divisibility $\binom{m+k}{k}\mid\binom{2m}{m}$ and studies it prime-by-prime. By Kummer's theorem, $ν_p\binom{2m}{m}$ translates into a carry count for doubling $m$ in base $p$. We then employ a counting argument to find, in each scale $[M,2M]$, an integer $m$ whose base-$p$ expansions simultaneously force many carries when doubling $m$, for every prime $p\le 2k$, while avoiding the rare event that one of $m+1,\dots,m+k$ is divisible by an unusually high power of $p$. These "carry-rich but spike-free" choices of $m$ force the needed $p$-adic inequalities and the divisibility. The overall strategy is similar to results regarding divisors of $\binom{2n}{n}$ studied earlier by Erdős and by Pomerance.
2601.07421
Jan 2026Number Theory
 2601.06868
2601.06868Complex Analysis and Riemann Surfaces: A Graduate Path to Algebraic Geometry
These lecture notes present a computation driven pathway from classical complex analysis to the theory of compact Riemann surfaces and their connections to algebraic geometry. The exposition follows a compute first then abstract philosophy, in which analytic and geometric structures are introduced through explicit calculations and local models before being organized into conceptual frameworks. The notes begin with the foundations of complex analysis, including holomorphic functions, Cauchy theory, power series, residues, and contour integration, with an emphasis on hands on techniques such as Laurent expansions, residue calculus, and branch cut methods. These analytic tools are then used to construct Riemann surfaces explicitly via branched coverings and gluing constructions, which serve as recurring test cases throughout the text. Differential forms, Stokes theorem, curvature, and the Gauss Bonnet theorem provide the geometric bridge to Hodge theory, culminating in a detailed and self contained treatment of the Hodge Weyl theorem on compact Riemann surfaces, including weak formulations, regularity, and concrete examples. The algebraic geometric core develops holomorphic line bundles, divisors, the Picard group, and sheaves, followed by Cech and sheaf cohomology, the exponential sequence, and de Rham and Dolbeault theories, all treated with explicit computations. The Riemann Roch theorem is presented with full proofs and applications, leading to the construction of the Jacobian, Abel Jacobi theory, theta functions, and the correspondence between Riemann surfaces, algebraic curves, and Galois coverings. Originating from collaborative study groups associated with the Enjoying Math community, these notes are intended for graduate students seeking a concrete and unified route from complex analysis to algebraic geometry.
2601.06868
Jan 2026Complex Variables
 2601.04934
2601.04934A classification of coadjoint orbits carrying Gibbs ensembles
A coadjoint orbit $O_λ\subseteq {\mathfrak g}^*$ of a Lie group $G$ is said to carry a Gibbs ensemble if the set of all $x \in {\mathfrak g}$, for which the function $α\mapsto e^{-α(x)}$ on the orbit is integrable with respect to the Liouville measure, has non-empty interior $Ω_λ$. We describe a classification of all coadjoint orbits of finite-dimensional Lie algebras with this property. In the context of Souriau's Lie group thermodynamics, the subset $Ω_λ$ is the geometric temperature, a parameter space for a family of Gibbs measures on the coadjoint orbit. The corresponding Fenchel--Legendre transform maps $Ω_λ/{\mathfrak z}({\mathfrak g})$ diffeomorphically onto the interior of the convex hull of the coadjoint orbit $O_λ$. This provides an interesting perspective on the underlying information geometry. We also show that already the integrability of $e^{-α(x)}$ for one $x \in {\mathfrak g}$ implies that $Ω_λ\not=\emptyset$ and that, for general Hamiltonian actions, the existence of Gibbs measures implies that the range of the momentum maps consists of coadjoint orbits $O_λ$ as above.
2601.04934
Jan 2026Symplectic Geometry
 2601.04161
2601.04161Ergodic Theorems and Equivalence of Green's Kernel for Random Walks in Random Environments
We study the Ergodic Properties of Random Walks in stationary ergodic environments without uniform ellipticity under a minimal assumption. There are two main components in our work. The first step is to adopt the arguments of Lawler to first prove a uniqueness principle. We use a more general definition of environments using~\textit{Environment Functions}. As a corollary, we can deduce an invariance principle under these assumptions for balanced environments under some assumptions. We also use the uniqueness principle to show that any balanced, elliptic random walk must have the same transience behaviour as the simple symmetric random walk. The second is to transfer the results we deduce in balanced environments to general ergodic environments(under some assumptions) using a control technique to derive a measure under which the \textit{local process} is stationary and ergodic. As a consequence of our results, we deduce the Law of Large Numbers for the Random Walk and an Invariance Principle under our assumptions.
2601.04161
Jan 2026Probability
Horn inequalities on a quiver with an involution
Derksen and Weyman described the cone of semi-invariants associated with a quiver. We give an inductive description of this cone, followed by an example of refinement of the inequalities characterising anti-invariant weights in the case of a quiver equipped with an involution.
2601.05089
Jan 2026Representation Theory
 2601.05228
2601.05228A Geometric Definition of the Integral and Applications
The standard definition of integration of differential forms is based on local coordinates and partitions of unity. This definition is mostly a formality and not used used in explicit computations or approximation schemes. We present a definition of the integral that uses triangulations instead. Our definition is a coordinate-free version of the standard definition of the Riemann integral on $\mathbb{R}^n$ and we argue that it is the natural definition in the contexts of Lie algebroids, stochastic integration and quantum field theory, where path integrals are defined using lattices. In particular, our definition naturally incorporates the different stochastic integrals, which involve integration over Hölder continuous paths. Furthermore, our definition is well-adapted to establishing integral identities from their combinatorial counterparts. Our construction is based on the observation that, in great generality, the things that are integrated are determined by cochains on the pair groupoid. Abstractly, our definition uses the van Est map to lift a differential form to the pair groupoid. Our construction suggests a generalization of the fundamental theorem of calculus which we prove: the singular cohomology and de Rham cohomology cap products of a cocycle with the fundamental class are equal.
2601.05228
Jan 2026Differential Geometry
 2601.00766
2601.00766Set mappings for general graphs
The study of extremal problems for set mappings has a long history. It was introduced in 1958 by Erdős and Hajnal, who considered the case of cliques in graphs and hypergraphs. Recently, Caro, Patkós, Tuza and Vizer revisited this subject, and initiated the systematic study of set mapping problems for general graphs. In this paper, we prove the following result, which answers one of their questions. Let $G$ be a graph with $m$ edges and no isolated vertices and let $f : E(K_N) \rightarrow E(K_N)$ such that $f(e)$ is disjoint from $e$ for all $e \in E(K_N)$. Then for some absolute constant $C$, as long as $N \geq C m$, there is a copy $G^*$ of $G$ in $K_N$ such that $f(e)$ is disjoint from $V(G^*)$ for all $e \in E(G^*)$. The bound $N = O(m)$ is tight for cliques and is tight up to a logarithmic factor for all $G$.
2601.00766
Jan 2026Combinatorics
 2601.00683
2601.00683The equivariant cohomology ring of the representation variety $\Hom(\Z^2,\mathrm{GL}_n(\C))$
We give a presentation of the $\mathrm{GL}_n(\C)$-equivariant cohomology ring with $\Z$-coefficients of the variety $\Hom(\Z^2,\mathrm{GL}_n(\C))\subseteq \mathrm{GL}_n(\C)^2$ for any $n$. It is torsion free and minimally generated as a $H^\ast B\mathrm{GL}_n(\C)$-algebra by $3n$ elements. The ideal of relations is the saturation of an $n$-generator ideal by even powers of the Vandermonde polynomial. For coefficients in a field whose characteristic does not divide $n!$, we also give a presentation of the non-equivariant cohomology ring of $\Hom(\Z^2,\mathrm{GL}_n(\C))$.
2601.00683
Jan 2026Algebraic Topology
Counterfactual Spaces
We mathematically axiomatise the stochastics of counterfactuals, by introducing two related frameworks, called counterfactual probability spaces and counterfactual causal spaces, which we collectively term counterfactual spaces. They are, respectively, probability and causal spaces whose underlying measurable spaces are products of world-specific measurable spaces. In contrast to more familiar accounts of counterfactuals founded on causal models, we do not view interventions as a necessary component of a theory of counterfactuals. As an alternative to Pearl's celebrated ladder of causation, we view counterfactuals and interventions are orthogonal concepts, respectively mathematised in counterfactual probability spaces and causal spaces. The two concepts are then combined to form counterfactual causal spaces. At the heart of our theory is the notion of shared information between the worlds, encoded completely within the probability measure and causal kernels, and whose extremes are characterised by independence and synchronisation of worlds. Compared to existing frameworks, counterfactual spaces enable the mathematical treatment of a strictly broader spectrum of counterfactuals.
2601.00507
Jan 2026Statistics Theory
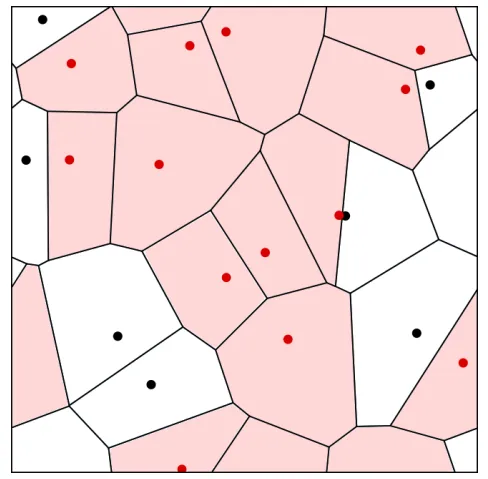
Voronoi Percolation: Topological Stability and Giant Cycles
We study the topological stability of Voronoi percolation in higher dimensions. We show that slightly increasing p allows a discretization that preserves increasing topological properties with high probability. This strengthens a theorem of Bollobás and Riordan and generalizes it to higher dimensions. As a consequence, we prove a sharp phase transition for the emergence of i-dimensional giant cycles in Voronoi percolation on the 2i-dimensional torus.
2601.00793
Jan 2026Probability
 2512.24920
2512.24920Transgression in the primitive cohomology
We study the Chern-Weil theory for the primitive cohomology of a symplectic manifold. First, given a symplectic manifold, we review the superbundle-valued forms on this manifold and prove a primitive version of the Bianchi identity. Second, as the main result, we prove a transgression formula associated with the boundary map of the primitive cohomology. Third, as an application of the main result, we introduce the concept of primitive characteristic classes and point out a further direction.
2512.24920
Dec 2025Differential Geometry
 2512.24152
2512.24152Score-based sampling without diffusions: Guidance from a simple and modular scheme
Sampling based on score diffusions has led to striking empirical results, and has attracted considerable attention from various research communities. It depends on availability of (approximate) Stein score functions for various levels of additive noise. We describe and analyze a modular scheme that reduces score-based sampling to solving a short sequence of ``nice'' sampling problems, for which high-accuracy samplers are known. We show how to design forward trajectories such that both (a) the terminal distribution, and (b) each of the backward conditional distribution is defined by a strongly log concave (SLC) distribution. This modular reduction allows us to exploit \emph{any} SLC sampling algorithm in order to traverse the backwards path, and we establish novel guarantees with short proofs for both uni-modal and multi-modal densities. The use of high-accuracy routines yields $\varepsilon$-accurate answers, in either KL or Wasserstein distances, with polynomial dependence on $\log(1/\varepsilon)$ and $\sqrt{d}$ dependence on the dimension.
2512.24152
Dec 2025Statistics Theory