Commutative Algebra

arXiv:math.AC

Commutative rings, modules, ideals, homological algebra, computational aspects, invariant theory, connections to algebraic geometry and combinatorics.

Trending in Commutative Algebra

Cellular free resolutions for normalizations of toric ideals

For any toric ideal $I$ in a polynomial ring $S$, we provide a combinatorial description of a free resolution of the integral closure of the $S$-module $S/I$. These new complexes arise from an extension of Bayer--Sturmfels' theory of cellular free resolutions. As applications, we unify several constructions for a resolution of the diagonal embedding of a toric variety, and compare the locally free resolutions for toric subvarieties introduced by Hanlon--Hicks--Lazarev and Brown--Erman.

2512.178711

Dec 2025Commutative Algebra

On a regularity-conjecture of generalized binomial edge ideals

In this paper, we prove the upper bound conjecture proposed by Saeedi Madani \& Kiani on the Castelnuovo-Mumford regularity of generalized binomial edge ideals. We give a combinatorial upper bound of regularity for generalized binomial edge ideals, which is better than the bound claimed in that conjecture. Also, we show that the bound is tight by providing an infinite class of graphs.

2512.015271

Dec 2025Commutative Algebra

2512.00648

A characteristic $p$ analog of formal lifting properties

A field extension $L/K$ of characteristic $p > 0$ is formally étale if and only if the relative Frobenius of $L/K$ is an isomorphism. Inspired by this classical result, we explore whether the formally étale property for a map $R \to S$ of $\mathbf{F}_p$-algebras is characterized by isomorphism of the relative Frobenius $F_{S/R}$. While $F_{S/R}$ being an isomorphism implies $R \to S$ is formally étale, the converse fails in the non-Noetherian setting. Thus, following Morrow, we introduce an enhancement of the formally étale property that we call b-nil (bounded nil) formally étale, and we show that $F_{S/R}$ is an isomorphism precisely when $R \to S$ is b-nil formally étale. We prove this result by first establishing several structural properties of b-nil formally smooth maps, which are defined analogously to the formally smooth case. Our structural results reveal that the b-nil formally smooth (resp. étale) property is quite different from the formally smooth (resp. étale) property. For instance, we show that any b-nil formally smooth algebra over an $F$-pure ring is reduced, whereas non-reduced formally étale algebras exist over $\mathbf{F}_p$ by a construction of Bhatt. We also show that the b-nil formally étale property neither implies nor is implied by having a trivial cotangent complex. We explore when formally smooth (resp. étale) implies b-nil formally smooth (resp. étale) in prime characteristic. A satisfactory picture emerges for ideal adic completions.

2512.006481

Nov 2025Commutative Algebra

Switching rook polynomial of collections of cells

We explore the novel connection between rook placements on collections of cells, also known as pruned chessboards, and the algebraic properties of ideals generated by $2$-minors. We design an algorithm to compute the switching rook polynomial of a collection of cells and show that it coincides with the $h$-polynomial of the associated coordinate ring for all collections up to rank 10 and polyominoes up to rank 12. Motivated by this evidence, we conjecture that the correspondence holds in general, and we prove it for certain convex collections of cells by algebraic tools.

2511.223462

Nov 2025Commutative Algebra

2511.17719

Separating versus ordinary Noether numbers

Let $G$ be a finite group and $K$ a field containing an element of multiplicative order $|G|$. It is shown that if $G$ has a cyclic subgroup of index at most $2$, then the separating Noether number over $K$ of $G$ coincides with the Noether number over $K$ of $G$. The same conclusion holds when $G$ is the direct product of a dihedral group and the $2$-element group. On the other hand, the smallest non-abelian groups $G$ are found for which the separating Noether number over $K$ is strictly less than the Noether number over $K$. Along the way the exact value of the separating Noether number is determined for all groups of order at most $16$. The results show in particular that unlike the ordinary Noether number, the separating Noether number of a non-abelian finite group may well be equal to the separating Noether number of a proper direct factor of the group.

2511.177191

Nov 2025Commutative Algebra

2511.07172

On finite orbits of infinite correspondences

These notes collect results about algebraic correspondences and adapt them to the setting of correspondences on projective lines. The focus lies on finite orbits of algebraic correspondences. The main result is a field theoretic characterization of the (in)finiteness of the number of finite orbits.

2511.071721

Nov 2025Commutative Algebra

2511.06482

Projective monomial curves associated to numerical semigroups with multiplicity $e$, width $e-1$, and embedding dimension $e-2$

Numerical semigroups with multiplicity $e$, width $e-1$, and embedding dimension $e-2$ are of the form $$S(e,m,n) = \langle \{e, e+1, \ldots, 2e-1\} \setminus \{e+m, e+n\} \rangle,$$ for some $1 \leq m < n \leq e-2$. Inspired by the work of Sally, Herzog and Stamate studied the special case $S(e,2,3)$, which they called the ``Sally numerical semigroups''. Recently, Dubey et. al. computed a minimal generating set of the defining ideal of the numerical semigroups $S(e,m,n)$ for $m \geq 2$. In this article, we first obtain an analog for the numerical semigroups $S(e,1,n)$, and then shift our focus to the projective monomial curves in $\mathbb{P}^{e-2}$ defined by the semigroups $S(e,m,n)$. We obtain a Gröbner basis for the defining ideal of the projective monomial curves associated to the semigroups $S(e,m,n)$. Moreover, we provide characterizations of Cohen--Macaulay and Gorenstein properties of these curves. Specifically, we prove that these are Cohen--Macaulay if and only if $(m,n) \neq (e-4,e-3)$, and Gorenstein if and only if $(e,m,n)\in \{ (4,1,2), (5,2,3)\}$. Furthermore, when these curves are Cohen--Macaulay, we compute the Castelnuovo--Mumford regularity of their coordinate ring.

2511.064822

Nov 2025Commutative Algebra

2511.02322

Graded perfectoid rings

We introduce and study graded perfectoid rings as graded analogues of Scholze's (integral) perfectoid rings. We establish a categorical equivalence between graded perfectoid rings and graded perfect prisms, extending the Bhatt-Scholze's correspondence to the graded setting. We also construct the initial graded perfectoid cover of any graded semiperfectoid rings and prove a graded version of André's flatness lemma. These results lay the foundations for a graded theory of perfectoid rings.

2511.023221

Nov 2025Commutative Algebra

An unrestricted notion of the finite factorization property

A nonzero element of an integral domain (or commutative cancellative monoid) is called atomic if it can be written as a finite product of irreducible elements (also called atoms). In this paper, we introduce and investigate an unrestricted version of the finite factorization property, extending the work on unrestricted UFDs carried out by Coykendall and Zafrullah who first studied unrestricted. An integral domain is said to have the unrestricted finite factorization (U-FF) property if every atomic element has only finitely many factorizations, or equivalently, if its atomic subring is a finite factorization domain (FFD). We position the property U-FF within the hierarchy of classical finiteness conditions, showing that every IDF domain is U-FF but not conversely, and we analyze its behavior under standard constructions. In particular, we determine necessary and sufficient conditions for the U-FF property to ascend along $D+M$ extensions, prove that nearly atomic IDF domains are FFDs, and construct an explicit example of an integral domain with the U-FF property whose polynomial ring is not U-FF. These results demonstrate that the U-FF property behaves analogously to the IDF property, while providing a finer interpolation between the IDF and the FF conditions.

2511.006911

Nov 2025Commutative Algebra

Generalized Additive Decompositions of Symmetric Tensors

This article addresses the Generalized Additive Decomposition (GAD) of symmetric tensors, that is, degree-$d$ forms $f \in \mathcal{S}_d$. From a geometric perspective, a GAD corresponds to representing a point on a secant of osculating varieties to the Veronese variety, providing a compact and structured description of a tensor that captures its intrinsic algebraic properties. We provide a linear algebra method for measuring the GAD size and prove that the minimal achievable size, which we call the GAD-rank of the considered tensor, coincides with the rank of suitable Catalecticant matrices, under certain regularity assumptions. We provide a new explicit description of the apolar scheme associated with a GAD as the annihilator of a polynomial-exponential series. We show that if the Castelnuovo-Mumford regularity of this scheme is sufficiently small, then both the GAD and the associated apolar scheme are minimal and unique. Leveraging these results, we develop a numerical GAD algorithm for symmetric tensors that effectively exploits the underlying algebraic structure, extending existing algebraic approaches based on eigen computation to the treatment of multiple points. We illustrate the effectiveness and numerical stability of such an algorithm through several examples, including Waring and tangential decompositions.

2510.256811

Oct 2025Commutative Algebra

GBNL: Graded Betti Number Learning of Complex Biological Data

While persistent homology is widely used for data shape analysis, persistent commutative algebra (PCA) has seen limited adoption in machine learning and data science. Unlike persistent homology, which delivers topological invariants in the form of Betti numbers, PCA provides both algebraic invariants and graded Betti numbers. However, graded Betti numbers have seldom been applied to real-world data. In this work, we introduce the first-of-its-kind application of commutative algebra graded Betti numbers in machine learning and data science. Specifically, we present Graded Betti Number Learning (GBNL) for protein-nucleic acid binding prediction. Protein-DNA/RNA interactions are fundamental to cellular processes such as replication, transcription, translation, and gene regulation, and their understanding and prediction remain challenging. GBNL represents each nucleic acid sequence as a family of $k$-mer-specific sets and derives persistent graded Betti invariants from PCA, generating multiscale topological representations of local nucleotide organization. To incorporate cross-molecule context, these graded Betti representations are paired with transformer-based protein embeddings, linking nucleotide-level signals with global protein patterns. The proposed graded Betti representations effectively detect single-site mutations and distinguish complete mutation patterns. Operating on primary sequences with minimal preprocessing, GBNL bridges commutative algebra, reduced algebraic topology, combinatorics, and machine learning, establishing a new paradigm for comparative sequence analysis. Numerical studies using three datasets highlight the success of GBNL in protein-nucleic acid binding prediction.

2510.231872

Oct 2025Commutative Algebra

The MacaulayPosets package for Macaulay2

We introduce the package MacaulayPosets written for the computational algebra system Macaulay2. This package utilized the poset data type introduced in the Posets package and offers functionality for studying the Macaulay property for posets, particularly those which arise as monomial posets of commutative rings. A Macaulay poset is characterized by a ranked structure and a total order that interacts harmoniously with the partial order, enabling the establishment of bounds on the sizes of subsets of a given rank within an order ideal.

2510.228431

Oct 2025Commutative Algebra

2510.20170

Characterization of almost Gorenstein rings in terms of the trace ideal

We provide a characterization of one-dimensional almost Gorenstein rings in terms of the trace ideal. As an application, we investigate the almost Gorenstein property of certain $\mathbb{Z}_2$-graded rings.

2510.201701

Oct 2025Commutative Algebra

Open Neighborhood Ideals of Well Totally Dominated Trees are Cohen-Macaulay

We introduce and investigate the open neighborhood ideal $\mathcal{N}(G)$ of a finite simple graph $G$. We describe the minimal primary decomposition of $\mathcal{N}(G)$ in terms of the minimal total dominating sets (TD-sets) of $G$. Then we prove that the open neighborhood ideal of a tree is Cohen-Macaulay if and only if the tree is unmixed (well totally dominated) and calculate the Cohen-Macaulay type. We also give a descriptive characterization of all unmixed trees which takes polynomial time to verify.

2510.197071

Oct 2025Commutative Algebra

2510.12708

Asymptotic Syzygies of Weighted Projective Spaces

By adapting methods of Ein-Erman-Lazarsfeld, we prove an analogue of the Ein-Lazarsfeld result on asymptotic syzygies for Veronese embeddings, in the setting of weighted projective spaces of the form $\mathbb{P}(1^n,2)$.

2510.127081

Oct 2025Commutative Algebra

2510.11668

Bounded powers of edge ideals: Gorenstein polytopes

Let $S=K[x_1, \ldots,x_n]$ denote the polynomial ring in $n$ variables over a field $K$ and $I(G) \subset S$ the edge ideal of a finite graph $G$ on $n$ vertices. Given a vector $\mathfrak{c}\in\mathbb{N}^n$ and an integer $q\geq 1$, we denote by $(I(G)^q)_{\mathfrak{c}}$ the ideal of $S$ generated by those monomials belonging to $I(G)^q$ whose exponent vectors are componentwise bounded above by $\mathfrak{c}$. Let $δ_{\mathfrak{c}}(I(G))$ denote the largest integer $q$ for which $(I(G)^q)_{\mathfrak{c}}\neq (0)$. Since $(I(G)^{δ_{\mathfrak{c}}(I)})_{\mathfrak{c}}$ is a polymatroidal ideal, it follows that its minimal set of monomial generators is the set of bases of a discrete polymatroid $\mathcal{D}(G,\mathfrak{c})$. In the present paper, a classification of Gorenstein polytopes of the form ${\rm conv}(\mathcal{D}(G,\mathfrak{c}))$ is studied.

2510.116681

Oct 2025Commutative Algebra

2510.11540

The Briançon-Skoda theorem for pseudo-rational and Du Bois singularities and uniformity in excellent rings

Suppose $J = (f_1, \dots, f_n)$ is an $n$-generated ideal in any ring $R$. We prove a general Briançon-Skoda-type containment relating the integral closure $\overline{J^{n+k-1}}$ with ordinary powers $J^k$. We prove that our result implies the full Briançon-Skoda containment $\overline{J^{n+k-1}} \subseteq J^k$ for pseudo-rational singularities (for instance regular rings), and even for the weaker condition of birational derived splinters. Our methods also yield the containment $\overline{J^{n+k}} \subseteq J^k$ for Du Bois singularities and even for a characteristic-free generalization. Our \myBrianconSkoda-type theorem also implies well-known closure-based Briançon-Skoda results $\overline{J^{n+k-1}} \subseteq (J^k)^{\mathrm{cl}}$ where, for instance, $\mathrm{cl}$ is tight or plus closure in characteristic $p > 0$, or $\mathrm{ep}$ closure or extension and contraction from $\widehat{R^+}$ in mixed characteristic. Our proof relies on a study of the tensor product of the derived image of the structure sheaf of a partially normalized blowup of $J$ with the Buchsbaum-Eisenbud complex (equivalently the Eagon-Northcott complex) associated to $(f_1,\dots,f_n)^k$. As an application of our results and methods above, we prove the uniform Artin-Rees theorem and the uniform Briançon-Skoda theorem for excellent, respectively excellent reduced, rings of finite dimension, answering conjectures of Huneke.

2510.115401

Oct 2025Commutative Algebra

2510.09969

The Graded Betti Numbers of the Skeletons of Simplicial Complexes

In this paper, we study a class $\mathcal{C}$ of squarefree monomial ideals $I\subseteq R=\mathbb{K}[x_1,\dots,x_n]$ over a field $\mathbb{K}$, defined by the condition that $\dim R/I$ equals the maximum degree of the minimal generators of $I$ minus one. We show that the Stanley-Reisner ideal of every $i$-skeleton of a simplicial complex $Δ$ belongs to $\mathcal{C}$ for all $-1\le i<\dimΔ$. To investigate their homological properties, we introduce the notion of a degree resolution and prove that every ideal in $\mathcal{C}$ possesses this property. Moreover, we show that every squarefree monomial ideal admits a truncation whose regularity coincides with that of the original ideal, thereby reducing the study of degree resolutions to that of linear resolutions. Finally, we provide an explicit formula describing the relationship between the graded Betti numbers of a simplicial complex and those of its skeletons.

2510.099691

Oct 2025Commutative Algebra

2510.05720

Annihilation of cohomology over one dimensional almost Gorenstein rings

Given a Cohen-Macaulay local ring, the cohomology annihilator ideal and the annihilator of the stable category of maximal Cohen-Macaulay modules are two ideals closely related both with each other and the singularities of the ring. Kimura recently showed that the two ideals agree up to radicals. In this article, we give a sufficient condition for the two ideals to be equal. As an application, we show that the cohomology annihilator ideal of a one dimensional analytically unramified almost Gorenstein complete local ring agrees with the conductor ideal.

2510.057201

Oct 2025Commutative Algebra

2510.04004

Remarks on effective uniform Briançon-Skoda

Let $R$ be a noetherian commutative ring. Of great interest is the question whether one can find an explicit integer $k$ such that $\overline{I^{k+n}}\subseteq I^n$ for each ideal $I$ and each integer $n\geq 1$ (the notation $\overline{I^{k+n}}$ denotes the integral closure of $I^{k+n}$). In this article, we investigate this question and obtain optimal values of $k$ for $F$-pure (or dense $F$-pure type) rings and Cohen-Macaulay $F$-injective (or dense $F$-injective type) rings.

2510.040041

Oct 2025Commutative Algebra

Related categories:

Algebraic Geometry Analysis of PDEs Algebraic Topology Classical Analysis and ODEs Combinatorics

229 papers

2601.03491

Quasi-$F^{\infty}$-split height versus quasi-$F$-regular height for rational double points and graded rings

In this paper, we study a phenomenon concerning quasi-$F$-singularities: under suitable hypotheses, the finiteness of the quasi-$F^{\infty}$-split height ($\mathrm{ht}^{\infty}$) implies quasi-$F$-regularity, and moreover, $\mathrm{ht}^{\infty}$ coincides with the quasi-$F$-regular height ($\mathrm{ht}^{\mathrm{reg}}$). We establish this coincidence for two important classes of isolated Gorenstein singularities. First, we explicitly compute $\mathrm{ht}^{\infty}$ and $\mathrm{ht}^{\mathrm{reg}}$ for all rational double points, showing that every non-$F$-pure rational double point satisfies $\mathrm{ht}^\infty = \mathrm{ht}^{\mathrm{reg}}$. Second, for localizations of graded non-$F$-pure normal Gorenstein rings with $F$-rational punctured spectrum, we again obtain the equality $\mathrm{ht}^\infty = \mathrm{ht}^{\mathrm{reg}}$.

2601.03491Jan 2026

View

2601.03208

Signature invariants of monomial ideals

Let $I$ be a monomial ideal of a polynomial ring $R=K[x_1,\ldots,x_n]$ over a field $K$ and let ${\rm sgn}(I)$ be its signature ideal. If $I$ is not a principal ideal, we show that the depth of $R/I$ is the depth of $R/{\rm sgn}(I)$, and the regularity of $R/{\rm sgn}(I)$ is at most the regularity of $R/I$. For ideals of height at least $2$, we show that the height and the associated primes of $I$ and its signature ${\rm sgn}(I)$ are the same, and we show that $I$ is Cohen--Macaulay (resp. Gorenstein) if and only if ${\rm sgn}(I)$ is Cohen--Macaulay (resp. Gorenstein), and furthermore we show that the v-number of ${\rm sgn}(I)$ is at most the v-number of $I$. We give an algorithm to compute the signature of a monomial ideal using \textit{Macaulay}$2$, and an algorithm to examine given families of monomial ideal by computing their signature ideals and determining which of these are either Cohen--Macaulay or Gorenstein.

2601.03208Jan 2026

View

Antidiagonal Initial Complexes of Infinite Matrix Schubert Varieties are Cohen-Macaulay

We show that, under certain constraints, the Stanley-Reisner ring of an infinite simplicial complex is Cohen-Macaulay in the sense of ideals and weak Bourbaki unmixed. We apply this result to prove the wanted claim -- that initial complexes of matrix Schubert varieties corresponding to infinite permutations in $S_{\infty}$ with respect to an antidiagonal term order are Cohen-Macaulay (in the same sense), giving rise to new examples of non-Noetherian Cohen-Macaulay rings.

2601.02612Jan 2026

View

2601.01120

Castelnuovo-Mumford regularity of generalized binomial edge ideals of graphs

In this paper, we mainly study the Castelnuovo-Mumford regularity of the generalized binomial edge ideals of graphs. We show that this number can be any integer number from $2$ to $n-1$ where $n$ is the number of vertices in the underlying graph. We are able to show this, after giving some tight lower and upper bounds for the regularity of generalized binomial edge ideals of the join product of graphs. In particular, we characterize all generalized binomial edge ideals with the regularity equal to~$2$ as well as extremal Gorenstein ideals. For this purpose, we give a new combinatorial characterization for the class of $P_4$-free graphs.

2601.01120Jan 2026

View

The variety of orthogonal frames

An orthogonal n-frame is an ordered set of n pairwise orthogonal vectors. The set of all orthogonal n-frames in a d-dimensional quadratic vector space is an algebraic variety V(d,n). In this paper, we investigate the variety V(d,n) as well as the quadratic ideal I(d,n) generated by the orthogonality relations, which cuts out V(d,n). We classify the irreducible components of V(d,n), give criteria for the ideal I(d,n) to be prime or a complete intersection, and for the variety V(d,n) to be normal. We also give near-equivalent conditions for V(d,n) to be factorial. Applications are given to the theory of Lovász-Saks-Schrijver ideals.

2512.25058Dec 2025

View

Arithmetic in the Boij Söderberg Cone

We study two long-standing conjectures concerning lower bounds for the Betti numbers of a graded module over a polynomial ring. We prove new cases of these conjectures in codimensions five and six by reframing the conjectures as arithmetic problems in the Boij-Söderberg cone. In this setting, potential counterexamples correspond to explicit Diophantine obstructions arising from the numerics of pure resolutions. Using number-theoretic methods, we completely classify these obstructions in the codimension three case revealing some delicate connections between Betti tables, commutative algebra and classical Diophantine equations. The new results in codimensions five and six concern Gorenstein algebras where a study of the variety determined by these Diophantine equations is sufficient to resolve the conjecture in this case.

2512.24320Dec 2025

View

2512.22940

Waldschmidt constant of monomial ideals and Simis ideals

In 2017, Cooper et al. proposed a conjecture providing a lower bound for the Waldschmidt constant of monomial ideals. We confirm this conjecture for some classes of monomial ideals. Recently, Méndez, Pinto, and Villarreal formulated a conjecture stating that if $I$ is a monomial ideal without embedded associated primes, whose irreducible decomposition is minimal and which is a Simis ideal, then there exist a Simis squarefree monomial ideal $J$ and a standard linear weighting $w$ such that $I = J_{w}.$ In this work, we verify this conjecture for some classes of monomial ideals.

2512.22940Dec 2025

View

Generalized binomial edge ideals are Cartwright-Sturmfels

Binomial edge ideals associated to a simple graph G were introduced by Herzog and collaborators and, independently, by Ohtani. They became an ``instant classic" in combinatorial commutative algebra with more than 100 papers devoted to their investigation over the past 15 years. They exhibit many striking properties, including being radical and, moreover, Cartwright-Sturmfels. Using the fact that binomial edge ideals can be seen as ideals of 2-minors of a matrix of variables with two rows, generalized binomial edge ideals of 2-minors of matrices of m rows were introduced by Rauh and proved to be radical. The goal of this paper is to prove that generalized binomial edge ideals are Cartwright-Sturmfels. On the way we provide results on ideal constructions preserving the Cartwright-Sturmfels property. We also give examples and counterexamples to the Cartwright-Sturmfels property for higher minors.

2512.22012Dec 2025

View

Non-finite generatedness of the congruences defined by tropical varieties

In tropical geometry, there are several important classes of ideals and congruences such as tropical ideals, bend congruences, and the congruences of the form $\mathbf E(Z)$. Although they are analogues of the concept of ideals of rings, it is not well known whether they are finitely generated. In this paper, we study whether the congruences of the form $\mathbf E(Z)$ are finitely generated. In particular, we show that when $Z$ is the support of a tropical variety, $\mathbf E(Z)$ is not finitely generated except for a few specific cases. In addition, we give an explicit minimal generating set of $\mathbf E(|L|)$ for the tropical standard line $L$.

2512.21565Dec 2025

View

2512.21550

The Gauss Algebra of squarefree Veronese algebras

We investigate the Gauss algebra for squarefree Veronese algebras generated in degree $3$. For small dimensions not exceeding $7$, we determine the Gauss algebra by specifying its generators and show in particular that it is normal and Cohen-Macaulay.

2512.21550Dec 2025

View

Minimal primes and radicality of ideals generated by adjacent 2-minors

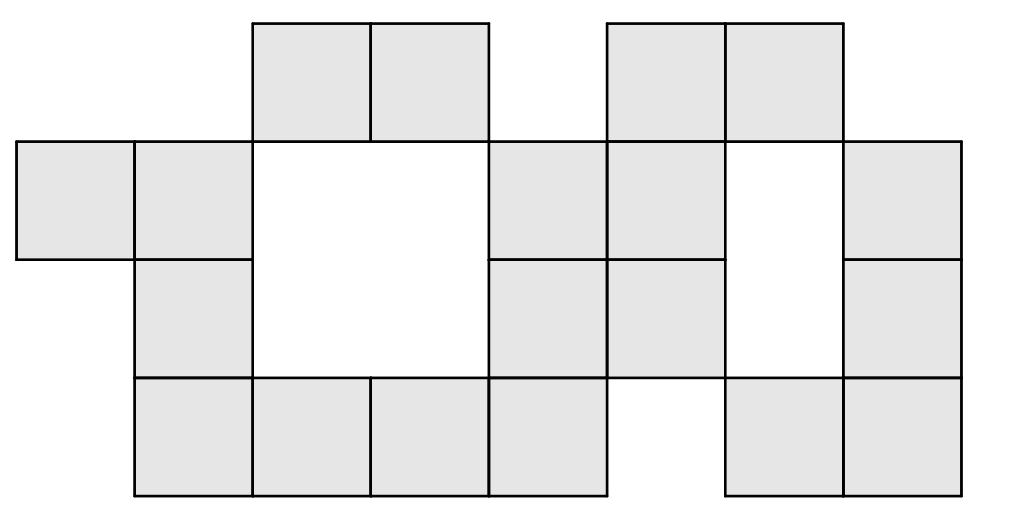
In this paper, we provide a complete description of the minimal primes of ideals generated by adjacent $2$-minors, in terms of the so-called admissible sets and associated lattice ideals. We prove that for these ideals, the properties of being unmixed, Cohen-Macaulay, level, Gorenstein, and complete intersection are equivalent. Moreover, we give a combinatorial characterization of all convex collections of cells satisfying any of these equivalent properties. Finally, we study the radicality of these ideals and derive necessary combinatorial conditions based on minimal non-radical configurations.

2512.21449Dec 2025

View

2512.20382

Fields of Fractions in Rigid Geometry

Let $A$ be an affinoid integral domain over a non-Archimedean field $K$, and let $L$ be its field of fractions. We prove that the normalization of $A$ can be reconstructed from $L$ by taking the intersection of all maximal discrete valuation subrings. As a corollary, taking the field of fractions induces a fully faithful functor from the category of normal affinoid integral domains over $K$ to the category of field extensions of $K$. This provides another $p$-adic analogue of the Riemann Hebbarkeitssatz.

2512.20382Dec 2025

View

Quasipolynomial behavior via constructability in multigraded algebra

Piecewise quasipolynomial growth of Presburger counting functions combines with tame persistent homology module theory to conclude piecewise quasipolynomial behavior of constructible families of finely graded modules over constructible commutative semigroup rings. Functorial preservation of constructibility for families under local cohomology, $\operatorname{Tor}$, and $\operatorname{Ext}$ yield piecewise quasipolynomial, quasilinear, or quasiconstant growth statements for length of local cohomology, $a$-invariants, regularity, depth; length of $\operatorname{Tor}$ and Betti numbers; length of $\operatorname{Ext}$ and Bass numbers; associated primes via $v$-invariants; and extended degrees, including the usual degree, Hilbert--Samuel multiplicity, arithmetic degree, and homological~degree.

2512.18536Dec 2025

View

2512.18506

Detecting and Quantifying Isolated Singularities over Discrete Valuation Rings

This paper develops a theory of isolated hypersurface singularities in mixed characteristic $(0,p)$, focusing on quotient rings over a Discrete Valuation Ring (DVR). We introduce and study analogues of the classical Tjurina and Milnor numbers for this setting, prove a generalized analogue of the determinacy theorem and the Mather-Yau Theorem for complete Noetherian local rings, and define numerical invariants that provide distinct criteria for detecting isolated singularities in the unramified and ramified cases.

2512.18506Dec 2025

View

Cellular free resolutions for normalizations of toric ideals

2512.178711Dec 2025

View

Persistent commutative algebra on graphs and hypergraphs

We introduce a persistent commutative algebra for studying the algebraic and combinatorial evolution of edge ideals of graphs and hypergraphs under filtration. Building on the Persistent Stanley--Reisner Theory (PSRT), we develop the notion of persistent edge ideals and analyze their graded Betti numbers across the filtration of graphs or hypergraphs. To enable this analysis, we establish a persistent extension of Hochster's formula, providing a functorial correspondence between algebraic and topological persistence. We further examine the behavior of Betti splittings in the persistent setting, proving a general inequality that extends the classical splitting result to the filtration of monomial ideals. Motivated by graph-theoretic interpretations, we introduce persistent minimal vertex covers, which encode the temporal structure of combinatorial dependencies within evolving graphs or hypergraphs. Applications to alignment-free genomic classification and molecular isomer discrimination demonstrate the interpretability and representatbility of persistent edge ideals as algebraic invariants, bridging combinatorial commutative algebra and data science.

2512.17619Dec 2025

View

2512.13452

Tropical Invariants for Permutation Group Actions

We consider the action of a permutation group $G$ of order $k$ on the tropical polynomial semiring in $n$ variables. We prove that the sub-semiring of invariant polynomials is finitely generated if and only if $G$ is generated by $2$-cycles. There do exist finitely many separating invariants of degree at most $\max\{n,{n\choose 2}\}$. Separating tropical invariants can be used to construct bi-Lipschitz embeddings of the orbit space ${\mathbb R}^n/G$ into Euclidean space. We also show that the invariant polynomials of degree $\leq n p_1p_2\cdots p_k$ generate the semifield of invariant rational tropical functions, where $p_1,p_2,\dots,p_k$ are the first $k$ prime numbers. Most results are also true over arbitrary semirings that are additively idempotent and multiplicatively cancellative.

2512.13452Dec 2025

View

2512.12986

Bounded powers of edge ideals: Pseudo-Gorenstein and Level polytopes

A lattice polytope $\mathcal{P} \subset \mathbb{R}^n$ of dimension $n$ is called level* if (i) $\mathcal{P}$ is normal, (ii) $(\mathcal{P} \setminus \partial \mathcal{P}) \cap \mathbb{Z}^n \neq \emptyset$ and (iii) for each $N = 2,3, \ldots$ and for each $\textbf{a} \in N(\mathcal{P} \setminus \partial \mathcal{P}) \cap \mathbb{Z}^n$, there is $\textbf{a}_0 \in (\mathcal{P} \setminus \partial \mathcal{P}) \cap \mathbb{Z}^n$ together with $\textbf{a}' \in (N-1)\mathcal{P} \cap \mathbb{Z}^n$ for which $\textbf{a} = \textbf{a}_0 + \textbf{a}'$, where $N\mathcal{P} = \{N\textbf{a} : \textbf{a} \in \mathcal{P}\}$. A normal polytope $\mathcal{P} \subset \mathbb{R}^n$ of dimension $n$ is called pseudo-Gorenstein* [4] if $ |(\mathcal{P} \setminus \partial \mathcal{P}) \cap \mathbb{Z}^n| = 1. $ A pseudo-Gorenstein* polytope $\mathcal{P}$ is level* if and only if $\mathcal{P}$ is reflexive up to translation. In the present paper, level* polytopes together with pseudo-Gorenstein* polytopes arising from discrete polymatroids of bounded powers of edge ideals are studied.

2512.12986Dec 2025

View

2512.11778

On strongly Koszul algebras and tidy Gröbner bases

Strongly Koszul algebras were introduced by Herzog, Hibi and Restuccia in 2000. The goal of the present paper is to provide an in-depth study of such algebras and to investigate how strong Koszulness interacts with the existence of a quadratic Gröbner basis for the defining ideal. Firstly, we prove that the existence of a quadratic revlex-universal Gröbner basis with a strong sparsity condition (that we name "tidiness") is a sufficient condition for strong Koszulness, and exhibit several concrete examples arising from determinantal objects and Macaulay's inverse system. We then prove that there exist standard graded algebras that are strongly Koszul but do not admit a Gröbner basis of quadrics even after a linear change of coordinates, thus answering negatively a question posed by Conca, De Negri and Rossi. As a bonus, we prove that strong Koszulness behaves well under tensor and fiber products of algebras and illustrate how Severi varieties and Macaulay's inverse system interact to produce examples of strongly Koszul algebras with a geometric flavor.

2512.11778Dec 2025

View

Free plane curves with a linear Jacobian syzygy

The study of planar free curves is a very active area of research, but a structural study of such a class is missing. We give a complete classification of the possible generators of the Jacobian syzygy module of a plane free curve under the assumption that one of them is linear. Specifically, we prove that, up to similarities, there are two possible forms for the Hilbert-Burch matrix. Our strategy relies on a translation of the problem into the accurate study of the geometry of maximal segments of a suitable triangle with integer points. Following this description, we are able to determine precisely the equations of free curves and the associated Hilbert-Burch matrices.

2512.10928Dec 2025

View

Page 1 of 12