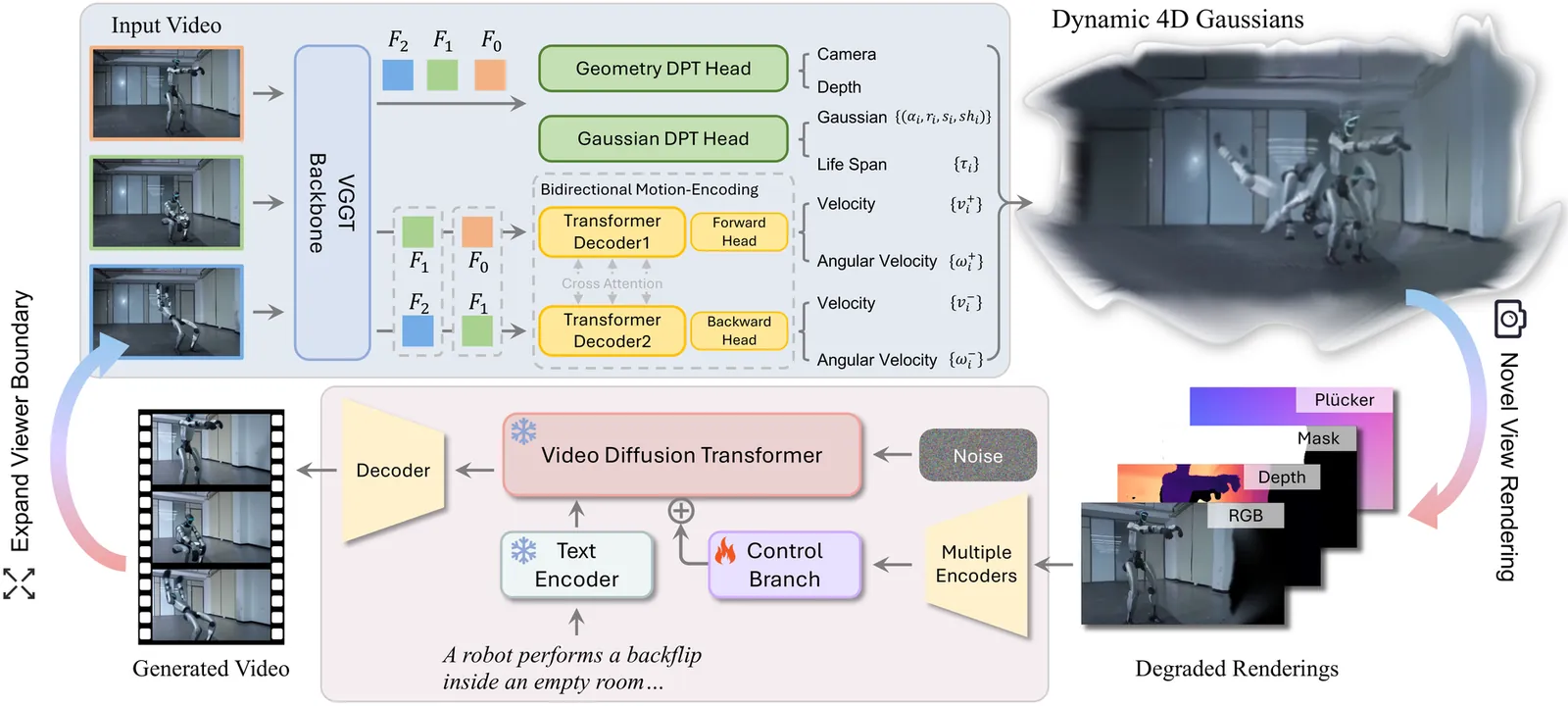
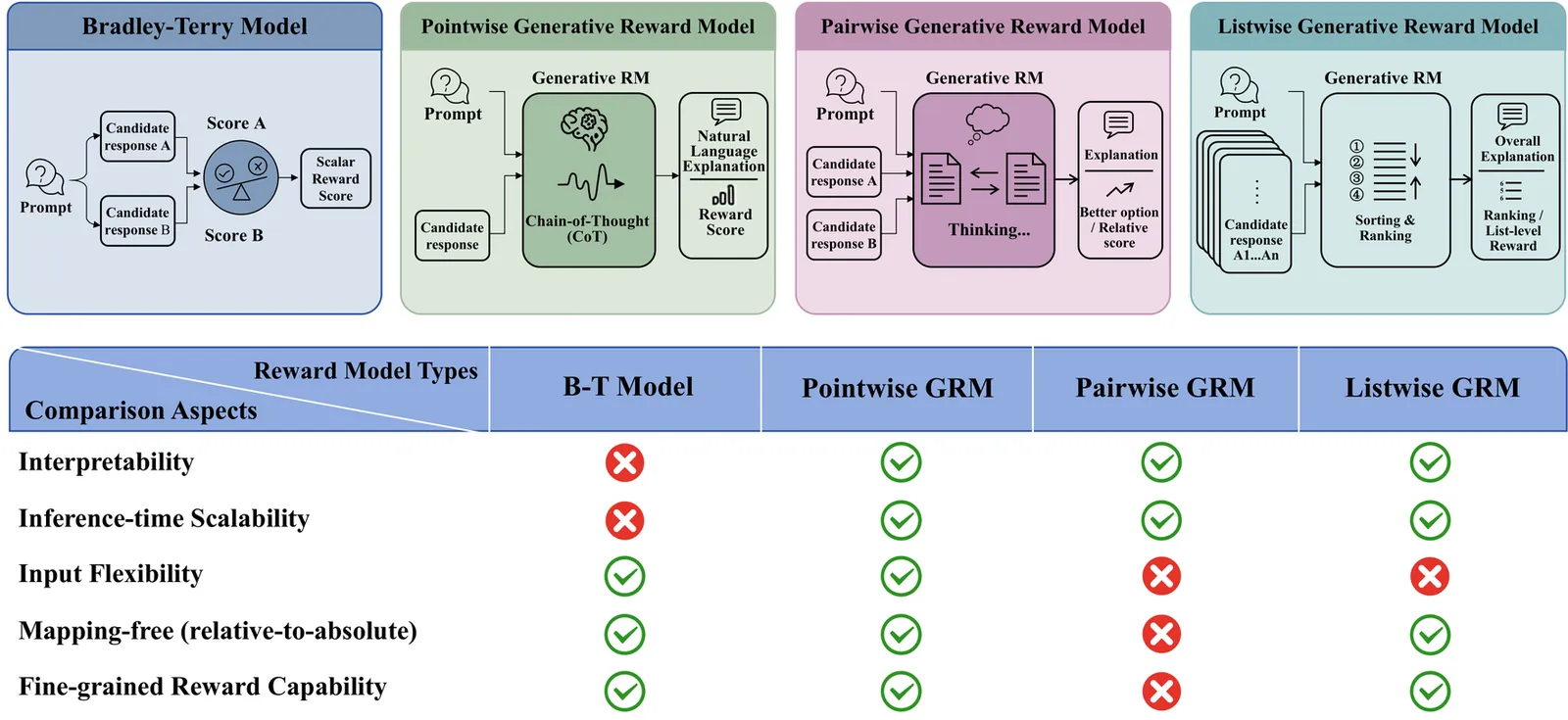
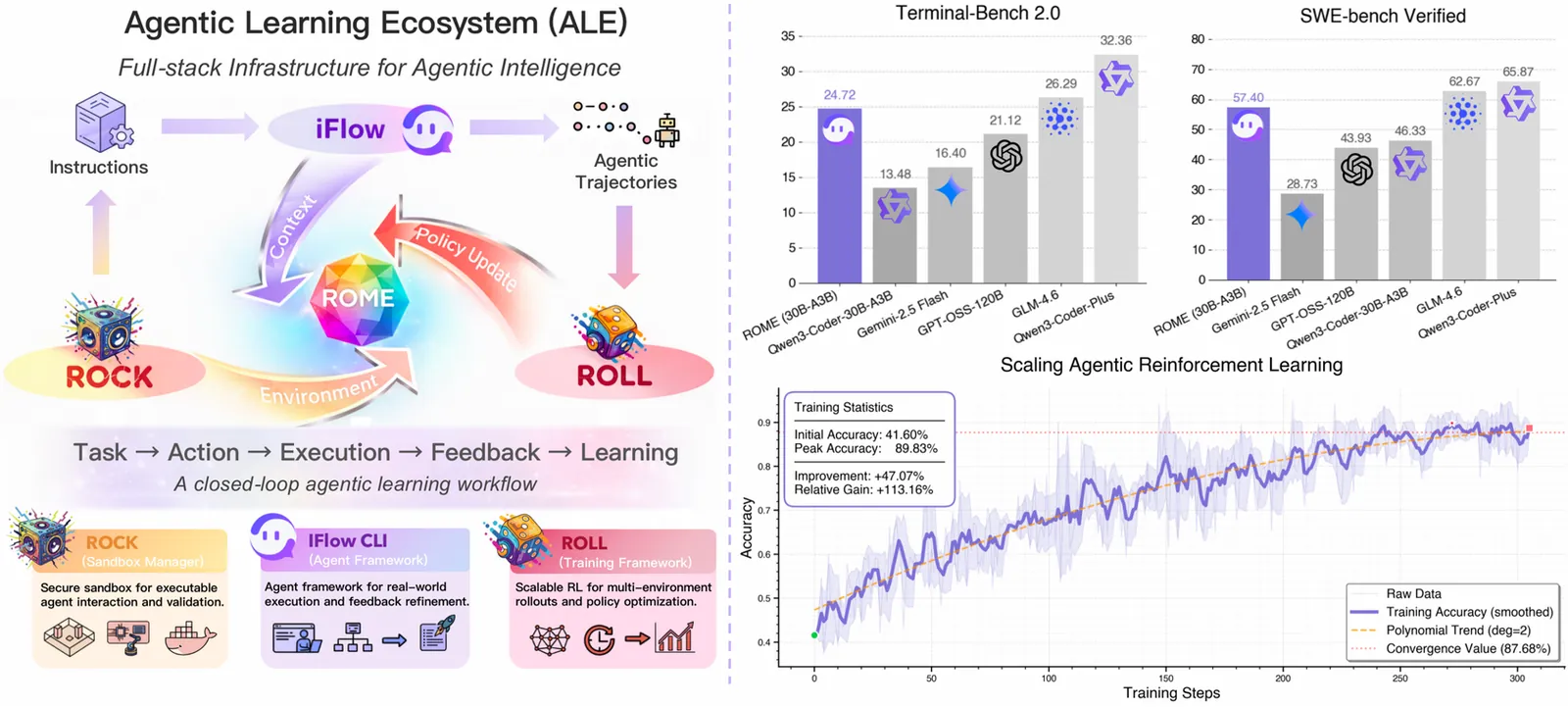
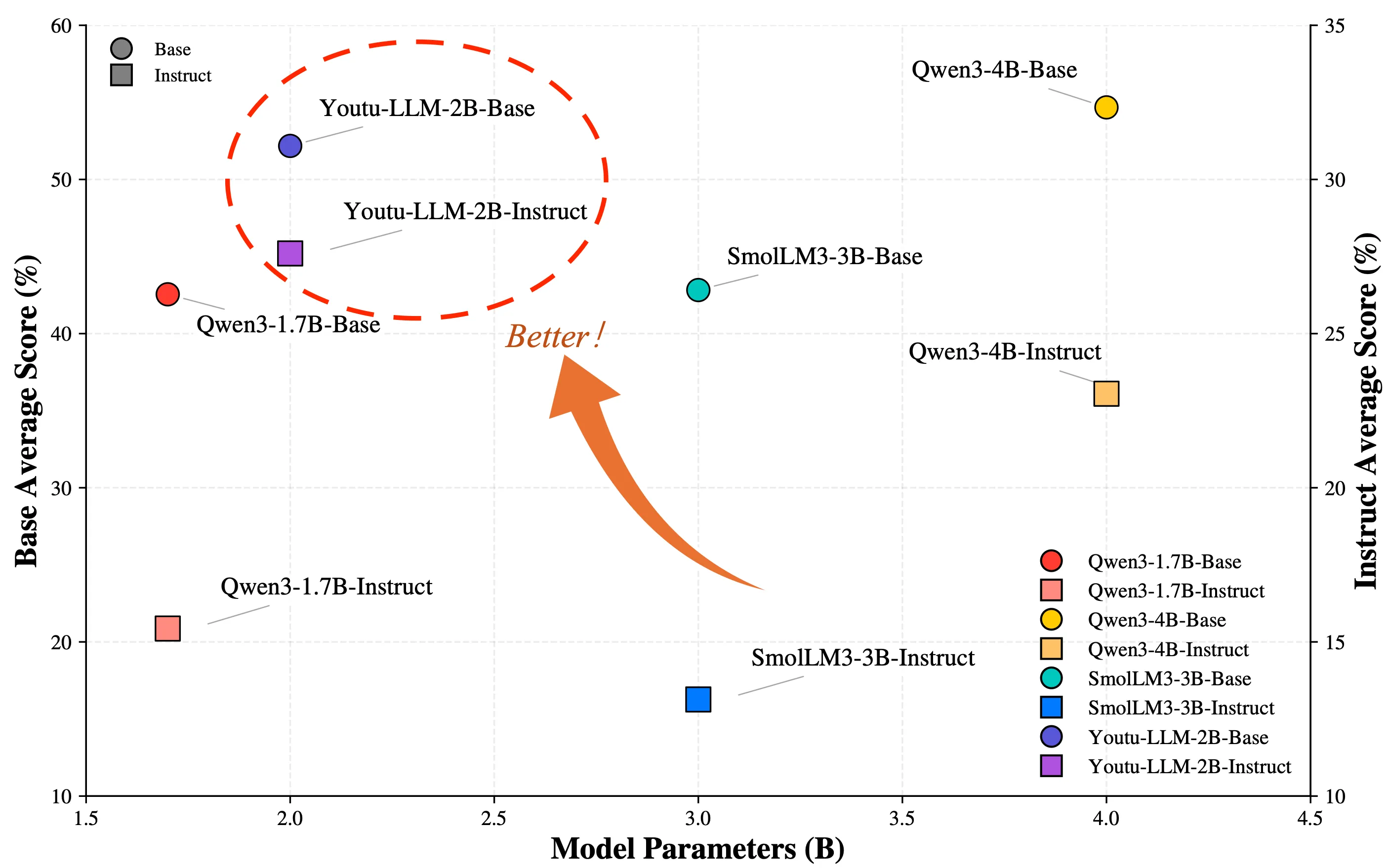
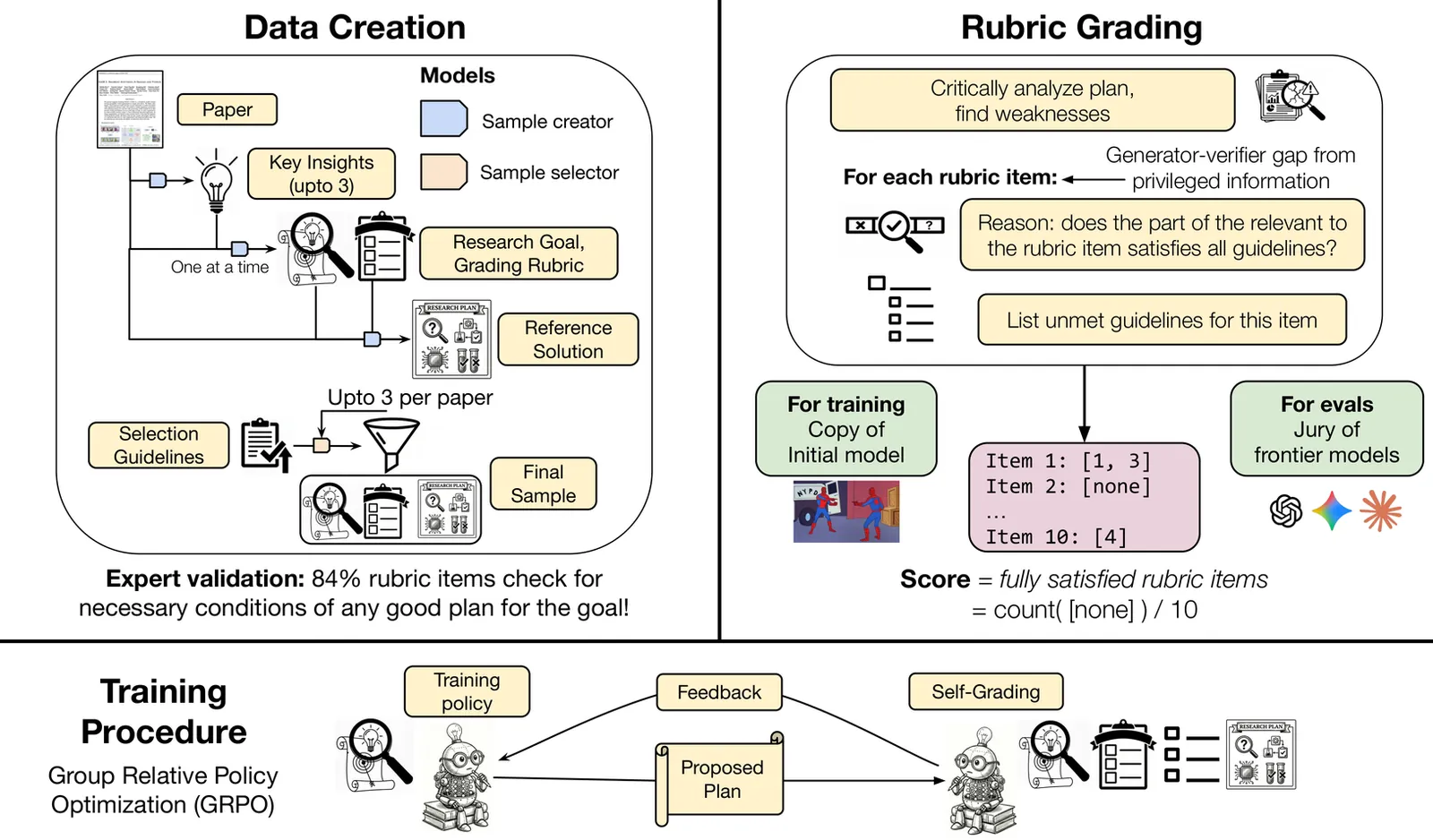
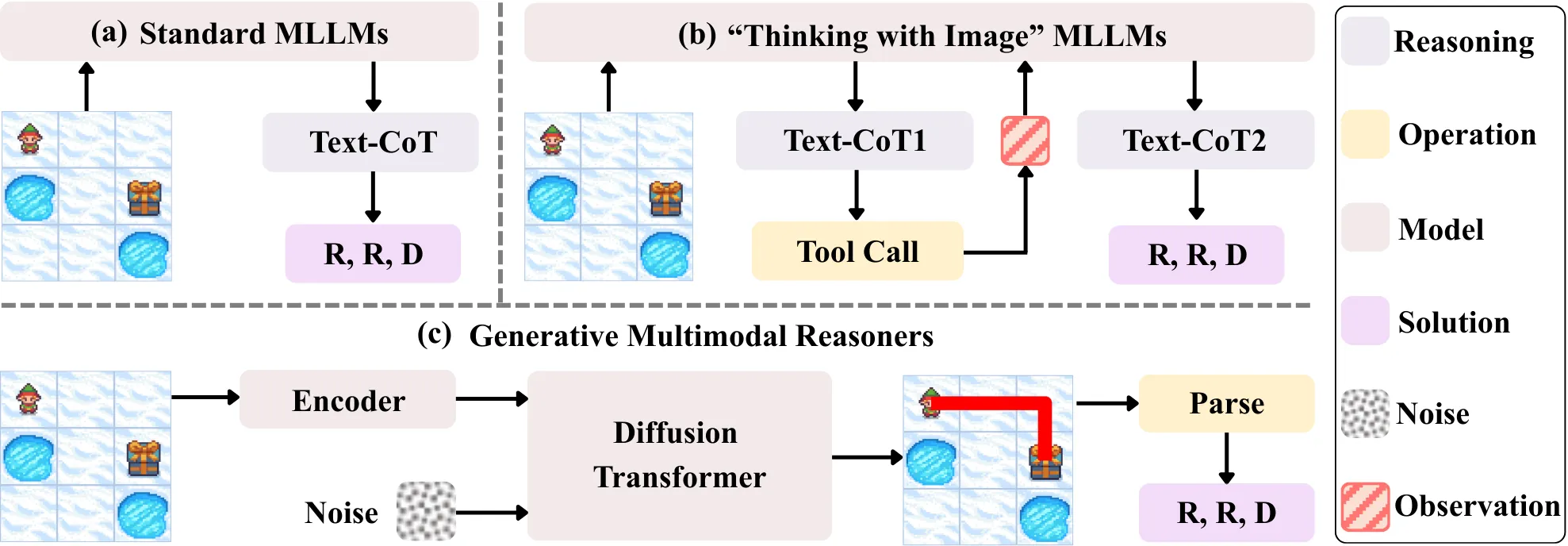
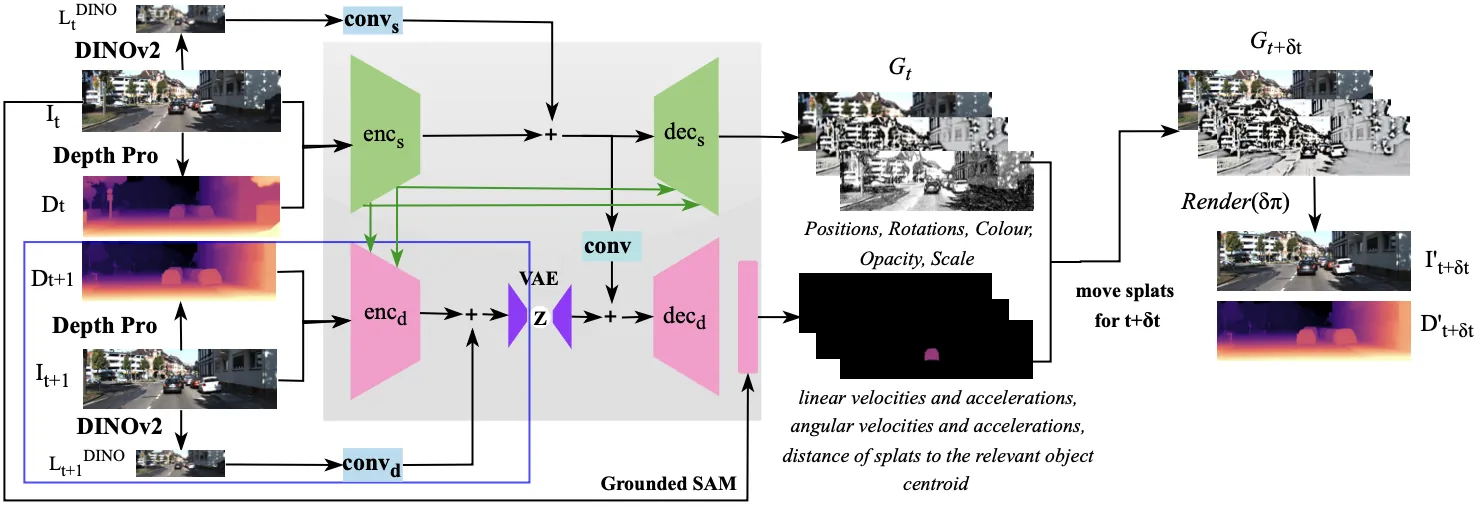
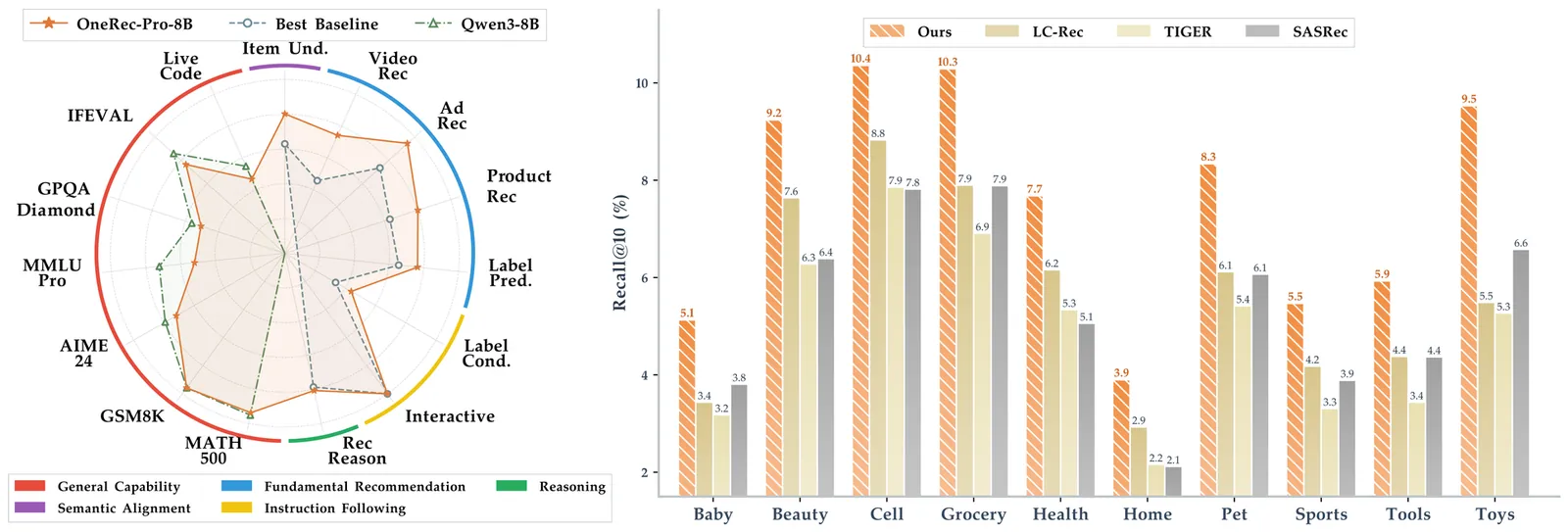
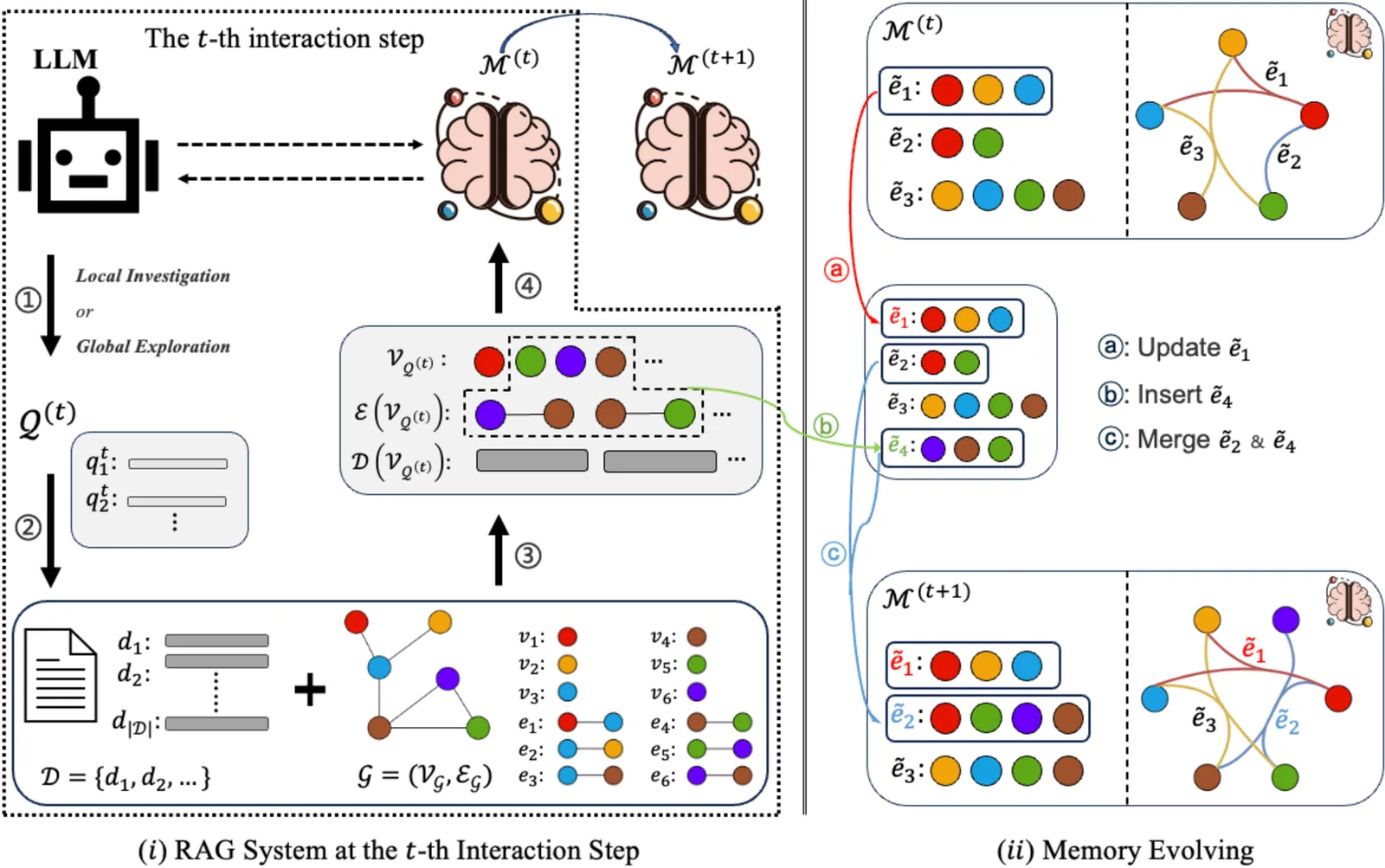
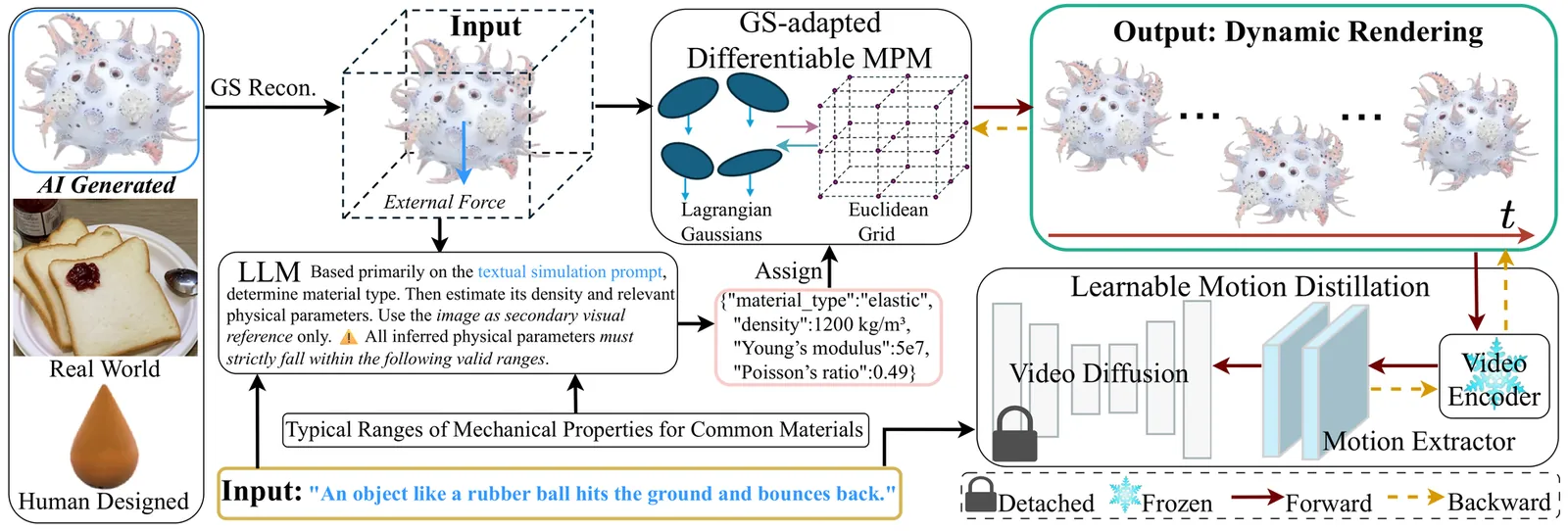
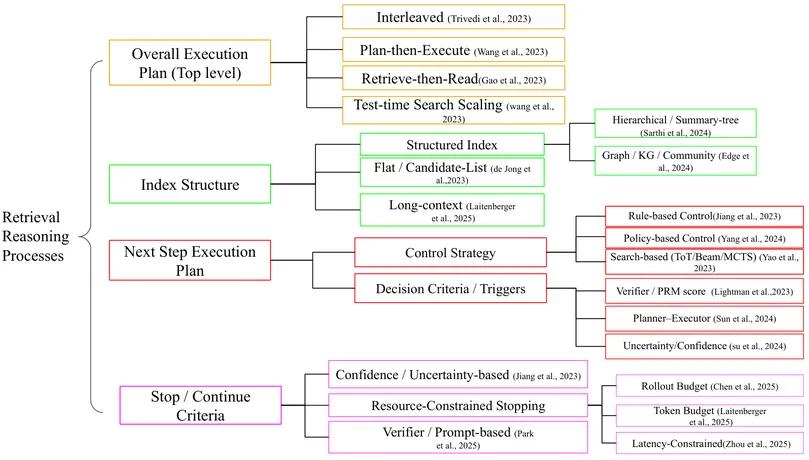
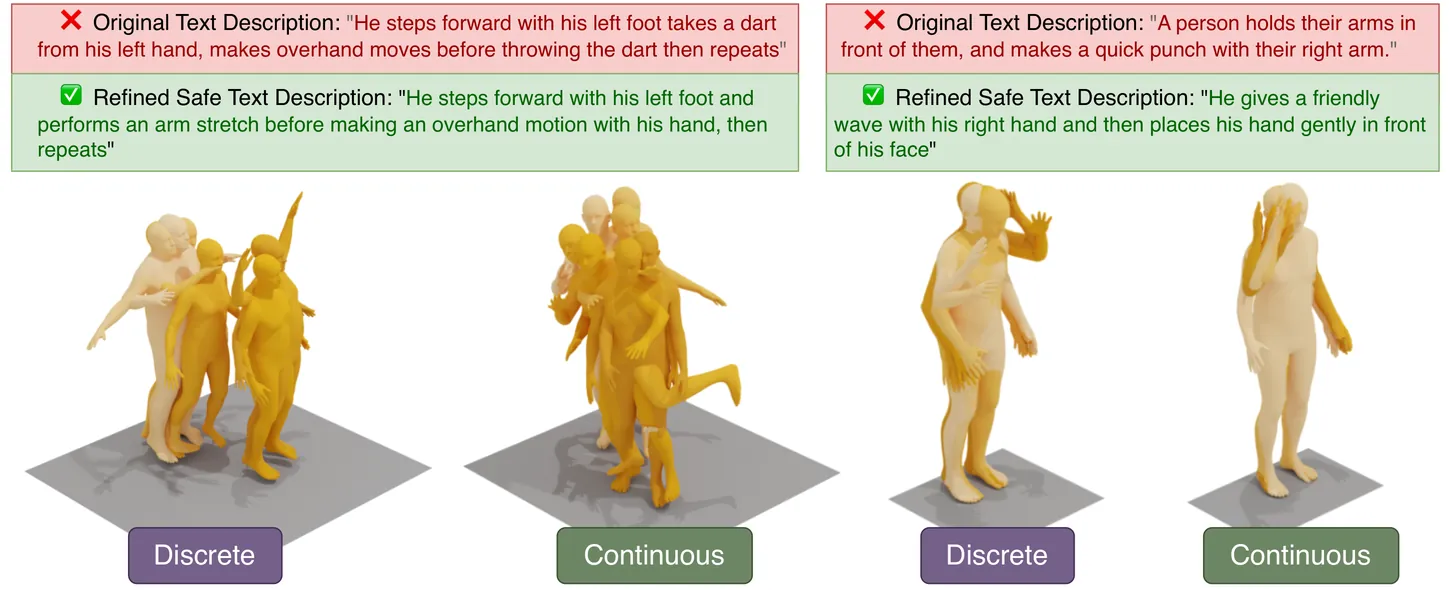
Explore Papers

Access 150k+ Papers via API, or Read as Interactive HTML

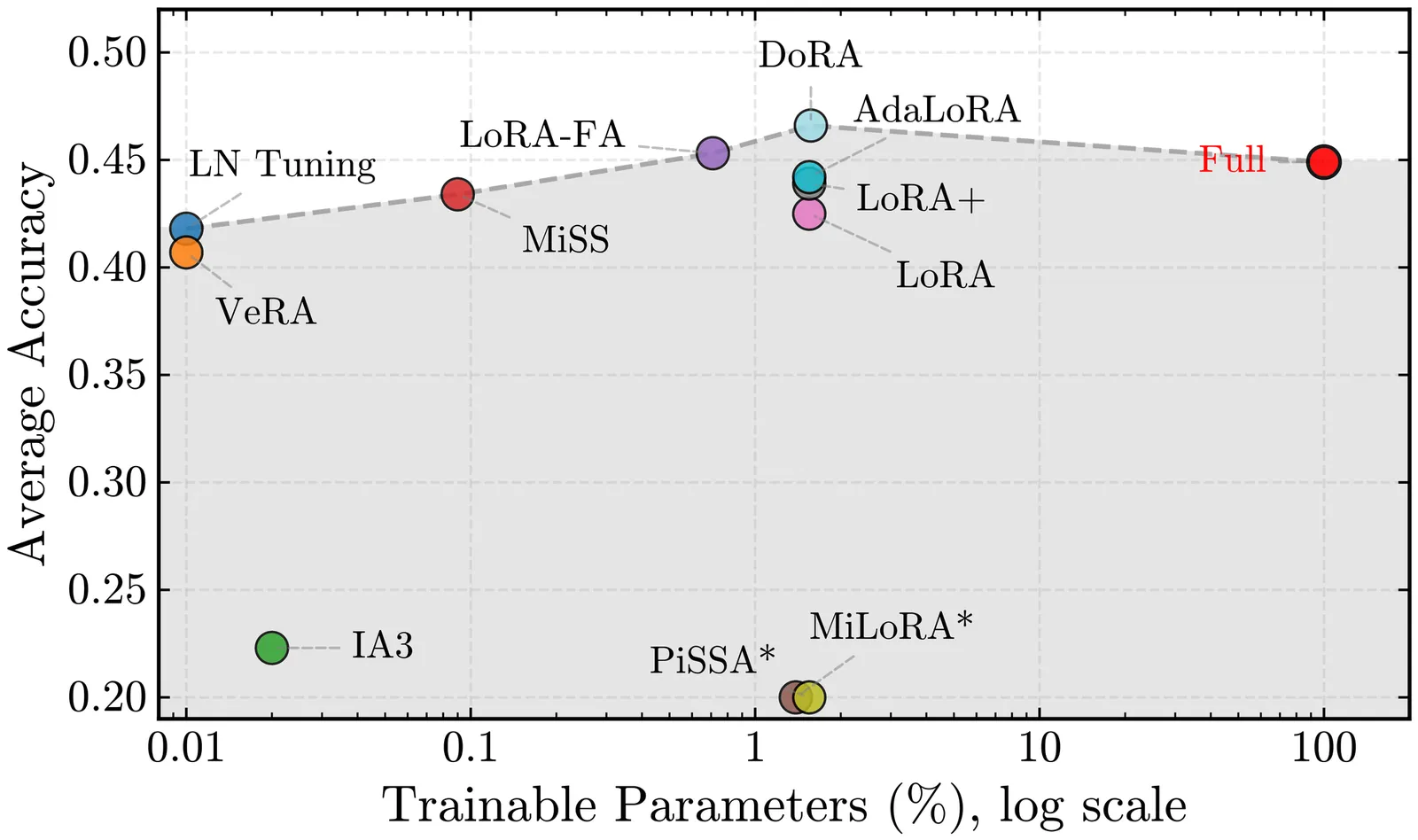
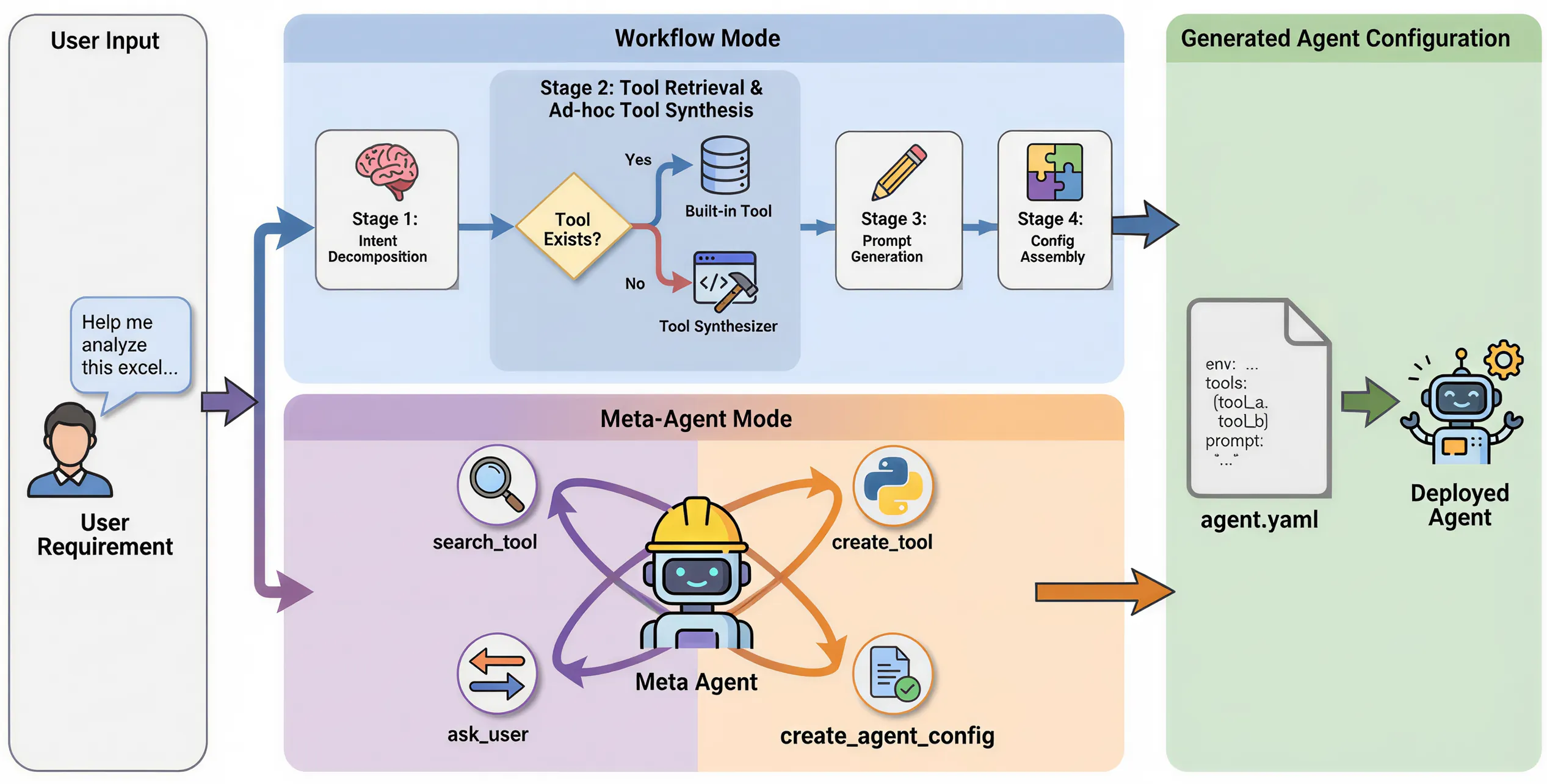
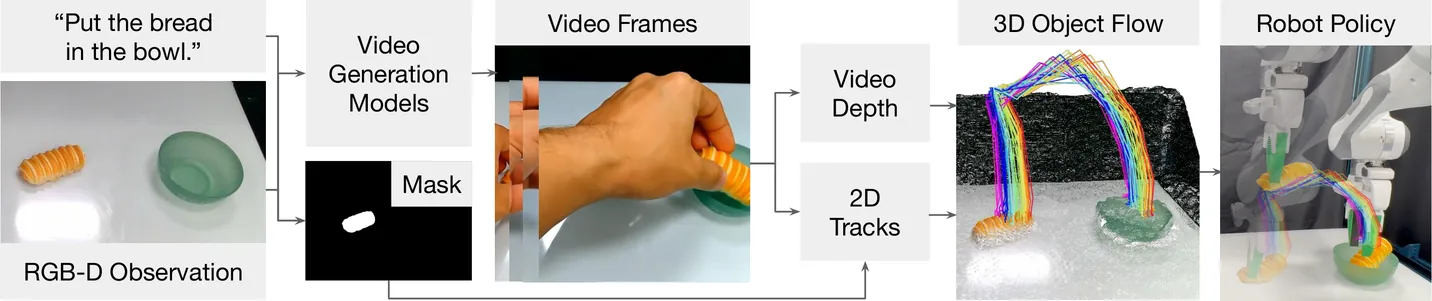
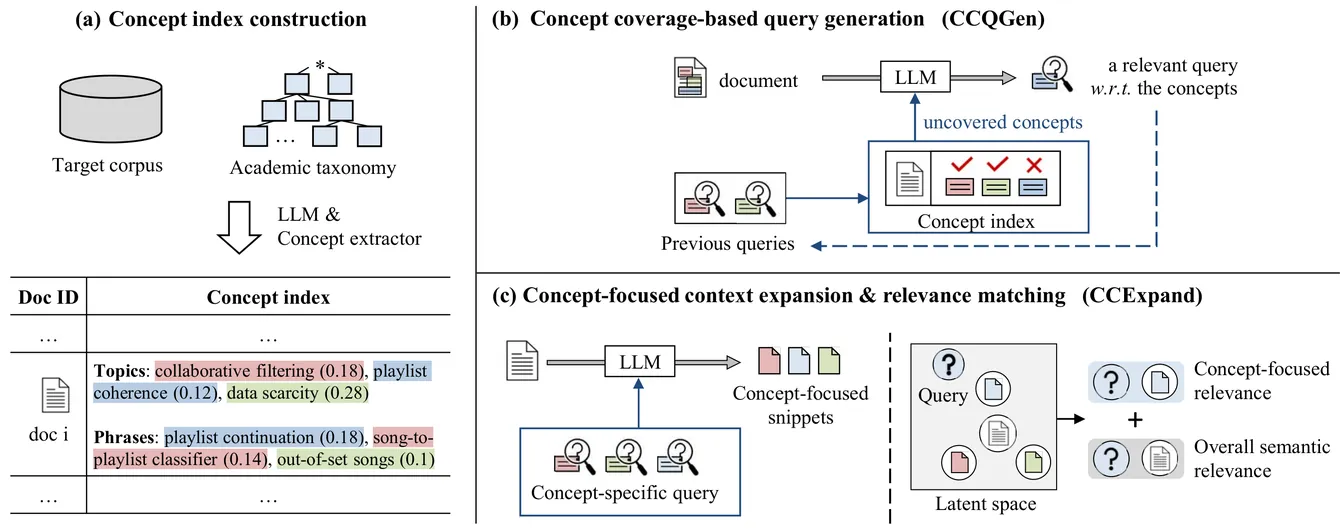
Trending Today

mHC: Manifold-Constrained Hyper-Connections

Recently, studies exemplified by Hyper-Connections (HC) have extended the ubiquitous residual connection paradigm established over the past decade by expanding the residual stream width and diversifying connectivity patterns. While yielding substantial performance gains, this diversification fundamentally compromises the identity mapping property intrinsic to the residual connection, which causes severe training instability and restricted scalability, and additionally incurs notable memory access overhead. To address these challenges, we propose Manifold-Constrained Hyper-Connections (mHC), a general framework that projects the residual connection space of HC onto a specific manifold to restore the identity mapping property, while incorporating rigorous infrastructure optimization to ensure efficiency. Empirical experiments demonstrate that mHC is effective for training at scale, offering tangible performance improvements and superior scalability. We anticipate that mHC, as a flexible and practical extension of HC, will contribute to a deeper understanding of topological architecture design and suggest promising directions for the evolution of foundational models.

2512.248801

Dec 2025Computation and Language

Recursive Language Models

We study allowing large language models (LLMs) to process arbitrarily long prompts through the lens of inference-time scaling. We propose Recursive Language Models (RLMs), a general inference strategy that treats long prompts as part of an external environment and allows the LLM to programmatically examine, decompose, and recursively call itself over snippets of the prompt. We find that RLMs successfully handle inputs up to two orders of magnitude beyond model context windows and, even for shorter prompts, dramatically outperform the quality of base LLMs and common long-context scaffolds across four diverse long-context tasks, while having comparable (or cheaper) cost per query.

2512.24601

Dec 2025Artificial Intelligence

Fast-weight Product Key Memory

Sequence modeling layers in modern language models typically face a trade-off between storage capacity and computational efficiency. While Softmax attention offers unbounded storage at prohibitive quadratic costs, linear variants provide efficiency but suffer from limited, fixed-size storage. We propose Fast-weight Product Key Memory (FwPKM), a novel architecture that resolves this tension by transforming the sparse Product Key Memory (PKM) from a static module into a dynamic, "fast-weight" episodic memory. Unlike PKM, FwPKM updates its parameters dynamically at both training and inference time via local chunk-level gradient descent, allowing the model to rapidly memorize and retrieve new key-value pairs from input sequences. Experiments reveal that FwPKM functions as an effective episodic memory that complements the semantic memory of standard modules, yielding significant perplexity reductions on long-context datasets. Notably, in Needle in a Haystack evaluations, FwPKM generalizes to 128K-token contexts despite being trained on only 4K-token sequences.

2601.00671

Jan 2026Computation and Language

Nested Learning: The Illusion of Deep Learning Architectures

Despite the recent progresses, particularly in developing Language Models, there are fundamental challenges and unanswered questions about how such models can continually learn/memorize, self-improve, and find effective solutions. In this paper, we present a new learning paradigm, called Nested Learning (NL), that coherently represents a machine learning model with a set of nested, multi-level, and/or parallel optimization problems, each of which with its own context flow. Through the lenses of NL, existing deep learning methods learns from data through compressing their own context flow, and in-context learning naturally emerges in large models. NL suggests a philosophy to design more expressive learning algorithms with more levels, resulting in higher-order in-context learning and potentially unlocking effective continual learning capabilities. We advocate for NL by presenting three core contributions: (1) Expressive Optimizers: We show that known gradient-based optimizers, such as Adam, SGD with Momentum, etc., are in fact associative memory modules that aim to compress the gradients' information (by gradient descent). Building on this insight, we present other more expressive optimizers with deep memory and/or more powerful learning rules; (2) Self-Modifying Learning Module: Taking advantage of NL's insights on learning algorithms, we present a sequence model that learns how to modify itself by learning its own update algorithm; and (3) Continuum Memory System: We present a new formulation for memory system that generalizes the traditional viewpoint of long/short-term memory. Combining our self-modifying sequence model with the continuum memory system, we present a continual learning module, called Hope, showing promising results in language modeling, knowledge incorporation, and few-shot generalization tasks, continual learning, and long-context reasoning tasks.

2512.246956

Dec 2025Machine Learning

Deep Delta Learning

The efficacy of deep residual networks is fundamentally predicated on the identity shortcut connection. While this mechanism effectively mitigates the vanishing gradient problem, it imposes a strictly additive inductive bias on feature transformations, thereby limiting the network's capacity to model complex state transitions. In this paper, we introduce Deep Delta Learning (DDL), a novel architecture that generalizes the standard residual connection by modulating the identity shortcut with a learnable, data-dependent geometric transformation. This transformation, termed the Delta Operator, constitutes a rank-1 perturbation of the identity matrix, parameterized by a reflection direction vector $\mathbf{k}(\mathbf{X})$ and a gating scalar $β(\mathbf{X})$. We provide a spectral analysis of this operator, demonstrating that the gate $β(\mathbf{X})$ enables dynamic interpolation between identity mapping, orthogonal projection, and geometric reflection. Furthermore, we restructure the residual update as a synchronous rank-1 injection, where the gate acts as a dynamic step size governing both the erasure of old information and the writing of new features. This unification empowers the network to explicitly control the spectrum of its layer-wise transition operator, enabling the modeling of complex, non-monotonic dynamics while preserving the stable training characteristics of gated residual architectures.

2601.004171

Jan 2026Machine Learning

RoboReward: General-Purpose Vision-Language Reward Models for Robotics

A well-designed reward is critical for effective reinforcement learning-based policy improvement. In real-world robotic domains, obtaining such rewards typically requires either labor-intensive human labeling or brittle, handcrafted objectives. Vision-language models (VLMs) have shown promise as automatic reward models, yet their effectiveness on real robot tasks is poorly understood. In this work, we aim to close this gap by introducing (1) \textbf{RoboReward}, a robotics reward dataset and benchmark built on large-scale real-robot corpora from Open X-Embodiment (OXE) and RoboArena, and (2) vision-language reward models trained on this dataset (RoboReward 4B/8B). Because OXE is success-heavy and lacks failure examples, we propose a \emph{negative examples data augmentation} pipeline that generates calibrated \emph{negatives} and \emph{near-misses} via counterfactual relabeling of successful episodes and temporal clipping to create partial-progress outcomes from the same videos. Using this framework, we produce an extensive training and evaluation dataset that spans diverse tasks and embodiments and enables systematic evaluation of whether state-of-the-art VLMs can reliably provide rewards for robotics. Our evaluation of leading open-weight and proprietary VLMs reveals that no model excels across all tasks, underscoring substantial room for improvement. We then train general-purpose 4B- and 8B-parameter models that outperform much larger VLMs in assigning rewards for short-horizon robotic tasks. Finally, we deploy the 8B-parameter reward VLM in real-robot reinforcement learning and find that it improves policy learning over Gemini Robotics-ER 1.5, a frontier physical reasoning VLM trained on robotics data, by a large margin, while substantially narrowing the gap to RL training with human-provided rewards.

2601.00675

Jan 2026Robotics

Dynamic Large Concept Models: Latent Reasoning in an Adaptive Semantic Space

Large Language Models (LLMs) apply uniform computation to all tokens, despite language exhibiting highly non-uniform information density. This token-uniform regime wastes capacity on locally predictable spans while under-allocating computation to semantically critical transitions. We propose $\textbf{Dynamic Large Concept Models (DLCM)}$, a hierarchical language modeling framework that learns semantic boundaries from latent representations and shifts computation from tokens to a compressed concept space where reasoning is more efficient. DLCM discovers variable-length concepts end-to-end without relying on predefined linguistic units. Hierarchical compression fundamentally changes scaling behavior. We introduce the first $\textbf{compression-aware scaling law}$, which disentangles token-level capacity, concept-level reasoning capacity, and compression ratio, enabling principled compute allocation under fixed FLOPs. To stably train this heterogeneous architecture, we further develop a $\textbf{decoupled $μ$P parametrization}$ that supports zero-shot hyperparameter transfer across widths and compression regimes. At a practical setting ($R=4$, corresponding to an average of four tokens per concept), DLCM reallocates roughly one-third of inference compute into a higher-capacity reasoning backbone, achieving a $\textbf{+2.69$\%$ average improvement}$ across 12 zero-shot benchmarks under matched inference FLOPs.

2512.24617

Dec 2025Machine Learning

Avatar Forcing: Real-Time Interactive Head Avatar Generation for Natural Conversation

Talking head generation creates lifelike avatars from static portraits for virtual communication and content creation. However, current models do not yet convey the feeling of truly interactive communication, often generating one-way responses that lack emotional engagement. We identify two key challenges toward truly interactive avatars: generating motion in real-time under causal constraints and learning expressive, vibrant reactions without additional labeled data. To address these challenges, we propose Avatar Forcing, a new framework for interactive head avatar generation that models real-time user-avatar interactions through diffusion forcing. This design allows the avatar to process real-time multimodal inputs, including the user's audio and motion, with low latency for instant reactions to both verbal and non-verbal cues such as speech, nods, and laughter. Furthermore, we introduce a direct preference optimization method that leverages synthetic losing samples constructed by dropping user conditions, enabling label-free learning of expressive interaction. Experimental results demonstrate that our framework enables real-time interaction with low latency (approximately 500ms), achieving 6.8X speedup compared to the baseline, and produces reactive and expressive avatar motion, which is preferred over 80% against the baseline.

2601.00664

Jan 2026Machine Learning

NeoVerse: Enhancing 4D World Model with in-the-wild Monocular Videos

In this paper, we propose NeoVerse, a versatile 4D world model that is capable of 4D reconstruction, novel-trajectory video generation, and rich downstream applications. We first identify a common limitation of scalability in current 4D world modeling methods, caused either by expensive and specialized multi-view 4D data or by cumbersome training pre-processing. In contrast, our NeoVerse is built upon a core philosophy that makes the full pipeline scalable to diverse in-the-wild monocular videos. Specifically, NeoVerse features pose-free feed-forward 4D reconstruction, online monocular degradation pattern simulation, and other well-aligned techniques. These designs empower NeoVerse with versatility and generalization to various domains. Meanwhile, NeoVerse achieves state-of-the-art performance in standard reconstruction and generation benchmarks. Our project page is available at https://neoverse-4d.github.io

2601.00393

Jan 2026Computer Vision

IRPO: Scaling the Bradley-Terry Model via Reinforcement Learning

Generative Reward Models (GRMs) have attracted considerable research interest in reward modeling due to their interpretability, inference-time scalability, and potential for refinement through reinforcement learning (RL). However, widely used pairwise GRMs create a computational bottleneck when integrated with RL algorithms such as Group Relative Policy Optimization (GRPO). This bottleneck arises from two factors: (i) the O(n^2) time complexity of pairwise comparisons required to obtain relative scores, and (ii) the computational overhead of repeated sampling or additional chain-of-thought (CoT) reasoning to improve performance. To address the first factor, we propose Intergroup Relative Preference Optimization (IRPO), a novel RL framework that incorporates the well-established Bradley-Terry model into GRPO. By generating a pointwise score for each response, IRPO enables efficient evaluation of arbitrarily many candidates during RL training while preserving interpretability and fine-grained reward signals. Experimental results demonstrate that IRPO achieves state-of-the-art (SOTA) performance among pointwise GRMs across multiple benchmarks, with performance comparable to that of current leading pairwise GRMs. Furthermore, we show that IRPO significantly outperforms pairwise GRMs in post-training evaluations.

2601.00677

Jan 2026Machine Learning

AdaGaR: Adaptive Gabor Representation for Dynamic Scene Reconstruction

Reconstructing dynamic 3D scenes from monocular videos requires simultaneously capturing high-frequency appearance details and temporally continuous motion. Existing methods using single Gaussian primitives are limited by their low-pass filtering nature, while standard Gabor functions introduce energy instability. Moreover, lack of temporal continuity constraints often leads to motion artifacts during interpolation. We propose AdaGaR, a unified framework addressing both frequency adaptivity and temporal continuity in explicit dynamic scene modeling. We introduce Adaptive Gabor Representation, extending Gaussians through learnable frequency weights and adaptive energy compensation to balance detail capture and stability. For temporal continuity, we employ Cubic Hermite Splines with Temporal Curvature Regularization to ensure smooth motion evolution. An Adaptive Initialization mechanism combining depth estimation, point tracking, and foreground masks establishes stable point cloud distributions in early training. Experiments on Tap-Vid DAVIS demonstrate state-of-the-art performance (PSNR 35.49, SSIM 0.9433, LPIPS 0.0723) and strong generalization across frame interpolation, depth consistency, video editing, and stereo view synthesis. Project page: https://jiewenchan.github.io/AdaGaR/

2601.00796

Jan 2026Computer Vision

Let It Flow: Agentic Crafting on Rock and Roll, Building the ROME Model within an Open Agentic Learning Ecosystem

Agentic crafting requires LLMs to operate in real-world environments over multiple turns by taking actions, observing outcomes, and iteratively refining artifacts. Despite its importance, the open-source community lacks a principled, end-to-end ecosystem to streamline agent development. We introduce the Agentic Learning Ecosystem (ALE), a foundational infrastructure that optimizes the production pipeline for agent LLMs. ALE consists of three components: ROLL, a post-training framework for weight optimization; ROCK, a sandbox environment manager for trajectory generation; and iFlow CLI, an agent framework for efficient context engineering. We release ROME (ROME is Obviously an Agentic Model), an open-source agent grounded by ALE and trained on over one million trajectories. Our approach includes data composition protocols for synthesizing complex behaviors and a novel policy optimization algorithm, Interaction-based Policy Alignment (IPA), which assigns credit over semantic interaction chunks rather than individual tokens to improve long-horizon training stability. Empirically, we evaluate ROME within a structured setting and introduce Terminal Bench Pro, a benchmark with improved scale and contamination control. ROME demonstrates strong performance across benchmarks like SWE-bench Verified and Terminal Bench, proving the effectiveness of the ALE infrastructure.

2512.24873

Dec 2025Artificial Intelligence

Youtu-LLM: Unlocking the Native Agentic Potential for Lightweight Large Language Models

We introduce Youtu-LLM, a lightweight yet powerful language model that harmonizes high computational efficiency with native agentic intelligence. Unlike typical small models that rely on distillation, Youtu-LLM (1.96B) is pre-trained from scratch to systematically cultivate reasoning and planning capabilities. The key technical advancements are as follows: (1) Compact Architecture with Long-Context Support: Built on a dense Multi-Latent Attention (MLA) architecture with a novel STEM-oriented vocabulary, Youtu-LLM supports a 128k context window. This design enables robust long-context reasoning and state tracking within a minimal memory footprint, making it ideal for long-horizon agent and reasoning tasks. (2) Principled "Commonsense-STEM-Agent" Curriculum: We curated a massive corpus of approximately 11T tokens and implemented a multi-stage training strategy. By progressively shifting the pre-training data distribution from general commonsense to complex STEM and agentic tasks, we ensure the model acquires deep cognitive abilities rather than superficial alignment. (3) Scalable Agentic Mid-training: Specifically for the agentic mid-training, we employ diverse data construction schemes to synthesize rich and varied trajectories across math, coding, and tool-use domains. This high-quality data enables the model to internalize planning and reflection behaviors effectively. Extensive evaluations show that Youtu-LLM sets a new state-of-the-art for sub-2B LLMs. On general benchmarks, it achieves competitive performance against larger models, while on agent-specific tasks, it significantly surpasses existing SOTA baselines, demonstrating that lightweight models can possess strong intrinsic agentic capabilities.

2512.24618

Dec 2025Computation and Language

Training AI Co-Scientists Using Rubric Rewards

AI co-scientists are emerging as a tool to assist human researchers in achieving their research goals. A crucial feature of these AI co-scientists is the ability to generate a research plan given a set of aims and constraints. The plan may be used by researchers for brainstorming, or may even be implemented after further refinement. However, language models currently struggle to generate research plans that follow all constraints and implicit requirements. In this work, we study how to leverage the vast corpus of existing research papers to train language models that generate better research plans. We build a scalable, diverse training corpus by automatically extracting research goals and goal-specific grading rubrics from papers across several domains. We then train models for research plan generation via reinforcement learning with self-grading. A frozen copy of the initial policy acts as the grader during training, with the rubrics creating a generator-verifier gap that enables improvements without external human supervision. To validate this approach, we conduct a study with human experts for machine learning research goals, spanning 225 hours. The experts prefer plans generated by our finetuned Qwen3-30B-A3B model over the initial model for 70% of research goals, and approve 84% of the automatically extracted goal-specific grading rubrics. To assess generality, we also extend our approach to research goals from medical papers, and new arXiv preprints, evaluating with a jury of frontier models. Our finetuning yields 12-22% relative improvements and significant cross-domain generalization, proving effective even in problem settings like medical research where execution feedback is infeasible. Together, these findings demonstrate the potential of a scalable, automated training recipe as a step towards improving general AI co-scientists.

2512.23707

Dec 2025Machine Learning

DiffThinker: Towards Generative Multimodal Reasoning with Diffusion Models

While recent Multimodal Large Language Models (MLLMs) have attained significant strides in multimodal reasoning, their reasoning processes remain predominantly text-centric, leading to suboptimal performance in complex long-horizon, vision-centric tasks. In this paper, we establish a novel Generative Multimodal Reasoning paradigm and introduce DiffThinker, a diffusion-based reasoning framework. Conceptually, DiffThinker reformulates multimodal reasoning as a native generative image-to-image task, achieving superior logical consistency and spatial precision in vision-centric tasks. We perform a systematic comparison between DiffThinker and MLLMs, providing the first in-depth investigation into the intrinsic characteristics of this paradigm, revealing four core properties: efficiency, controllability, native parallelism, and collaboration. Extensive experiments across four domains (sequential planning, combinatorial optimization, constraint satisfaction, and spatial configuration) demonstrate that DiffThinker significantly outperforms leading closed source models including GPT-5 (+314.2\%) and Gemini-3-Flash (+111.6\%), as well as the fine-tuned Qwen3-VL-32B baseline (+39.0\%), highlighting generative multimodal reasoning as a promising approach for vision-centric reasoning.

2512.24165

Dec 2025Computer Vision

Pixel-to-4D: Camera-Controlled Image-to-Video Generation with Dynamic 3D Gaussians

Humans excel at forecasting the future dynamics of a scene given just a single image. Video generation models that can mimic this ability are an essential component for intelligent systems. Recent approaches have improved temporal coherence and 3D consistency in single-image-conditioned video generation. However, these methods often lack robust user controllability, such as modifying the camera path, limiting their applicability in real-world applications. Most existing camera-controlled image-to-video models struggle with accurately modeling camera motion, maintaining temporal consistency, and preserving geometric integrity. Leveraging explicit intermediate 3D representations offers a promising solution by enabling coherent video generation aligned with a given camera trajectory. Although these methods often use 3D point clouds to render scenes and introduce object motion in a later stage, this two-step process still falls short in achieving full temporal consistency, despite allowing precise control over camera movement. We propose a novel framework that constructs a 3D Gaussian scene representation and samples plausible object motion, given a single image in a single forward pass. This enables fast, camera-guided video generation without the need for iterative denoising to inject object motion into render frames. Extensive experiments on the KITTI, Waymo, RealEstate10K and DL3DV-10K datasets demonstrate that our method achieves state-of-the-art video quality and inference efficiency. The project page is available at https://melonienimasha.github.io/Pixel-to-4D-Website.

2601.00678

Jan 2026Computer Vision

OpenOneRec Technical Report

While the OneRec series has successfully unified the fragmented recommendation pipeline into an end-to-end generative framework, a significant gap remains between recommendation systems and general intelligence. Constrained by isolated data, they operate as domain specialists-proficient in pattern matching but lacking world knowledge, reasoning capabilities, and instruction following. This limitation is further compounded by the lack of a holistic benchmark to evaluate such integrated capabilities. To address this, our contributions are: 1) RecIF Bench & Open Data: We propose RecIF-Bench, a holistic benchmark covering 8 diverse tasks that thoroughly evaluate capabilities from fundamental prediction to complex reasoning. Concurrently, we release a massive training dataset comprising 96 million interactions from 160,000 users to facilitate reproducible research. 2) Framework & Scaling: To ensure full reproducibility, we open-source our comprehensive training pipeline, encompassing data processing, co-pretraining, and post-training. Leveraging this framework, we demonstrate that recommendation capabilities can scale predictably while mitigating catastrophic forgetting of general knowledge. 3) OneRec-Foundation: We release OneRec Foundation (1.7B and 8B), a family of models establishing new state-of-the-art (SOTA) results across all tasks in RecIF-Bench. Furthermore, when transferred to the Amazon benchmark, our models surpass the strongest baselines with an average 26.8% improvement in Recall@10 across 10 diverse datasets (Figure 1). This work marks a step towards building truly intelligent recommender systems. Nonetheless, realizing this vision presents significant technical and theoretical challenges, highlighting the need for broader research engagement in this promising direction.

2512.24762

Dec 2025Information Retrieval

Evaluating Parameter Efficient Methods for RLVR

We systematically evaluate Parameter-Efficient Fine-Tuning (PEFT) methods under the paradigm of Reinforcement Learning with Verifiable Rewards (RLVR). RLVR incentivizes language models to enhance their reasoning capabilities through verifiable feedback; however, while methods like LoRA are commonly used, the optimal PEFT architecture for RLVR remains unidentified. In this work, we conduct the first comprehensive evaluation of over 12 PEFT methodologies across the DeepSeek-R1-Distill families on mathematical reasoning benchmarks. Our empirical results challenge the default adoption of standard LoRA with three main findings. First, we demonstrate that structural variants, such as DoRA, AdaLoRA, and MiSS, consistently outperform LoRA. Second, we uncover a spectral collapse phenomenon in SVD-informed initialization strategies (\textit{e.g.,} PiSSA, MiLoRA), attributing their failure to a fundamental misalignment between principal-component updates and RL optimization. Furthermore, our ablations reveal that extreme parameter reduction (\textit{e.g.,} VeRA, Rank-1) severely bottlenecks reasoning capacity. We further conduct ablation studies and scaling experiments to validate our findings. This work provides a definitive guide for advocating for more exploration for parameter-efficient RL methods.

2512.23165

Dec 2025Machine Learning

Youtu-Agent: Scaling Agent Productivity with Automated Generation and Hybrid Policy Optimization

Existing Large Language Model (LLM) agent frameworks face two significant challenges: high configuration costs and static capabilities. Building a high-quality agent often requires extensive manual effort in tool integration and prompt engineering, while deployed agents struggle to adapt to dynamic environments without expensive fine-tuning. To address these issues, we propose \textbf{Youtu-Agent}, a modular framework designed for the automated generation and continuous evolution of LLM agents. Youtu-Agent features a structured configuration system that decouples execution environments, toolkits, and context management, enabling flexible reuse and automated synthesis. We introduce two generation paradigms: a \textbf{Workflow} mode for standard tasks and a \textbf{Meta-Agent} mode for complex, non-standard requirements, capable of automatically generating tool code, prompts, and configurations. Furthermore, Youtu-Agent establishes a hybrid policy optimization system: (1) an \textbf{Agent Practice} module that enables agents to accumulate experience and improve performance through in-context optimization without parameter updates; and (2) an \textbf{Agent RL} module that integrates with distributed training frameworks to enable scalable and stable reinforcement learning of any Youtu-Agents in an end-to-end, large-scale manner. Experiments demonstrate that Youtu-Agent achieves state-of-the-art performance on WebWalkerQA (71.47\%) and GAIA (72.8\%) using open-weight models. Our automated generation pipeline achieves over 81\% tool synthesis success rate, while the Practice module improves performance on AIME 2024/2025 by +2.7\% and +5.4\% respectively. Moreover, our Agent RL training achieves 40\% speedup with steady performance improvement on 7B LLMs, enhancing coding/reasoning and searching capabilities respectively up to 35\% and 21\% on Maths and general/multi-hop QA benchmarks.

2512.24615

Dec 2025Artificial Intelligence

Dream2Flow: Bridging Video Generation and Open-World Manipulation with 3D Object Flow

Generative video modeling has emerged as a compelling tool to zero-shot reason about plausible physical interactions for open-world manipulation. Yet, it remains a challenge to translate such human-led motions into the low-level actions demanded by robotic systems. We observe that given an initial image and task instruction, these models excel at synthesizing sensible object motions. Thus, we introduce Dream2Flow, a framework that bridges video generation and robotic control through 3D object flow as an intermediate representation. Our method reconstructs 3D object motions from generated videos and formulates manipulation as object trajectory tracking. By separating the state changes from the actuators that realize those changes, Dream2Flow overcomes the embodiment gap and enables zero-shot guidance from pre-trained video models to manipulate objects of diverse categories-including rigid, articulated, deformable, and granular. Through trajectory optimization or reinforcement learning, Dream2Flow converts reconstructed 3D object flow into executable low-level commands without task-specific demonstrations. Simulation and real-world experiments highlight 3D object flow as a general and scalable interface for adapting video generation models to open-world robotic manipulation. Videos and visualizations are available at https://dream2flow.github.io/.

2512.24766

Dec 2025Robotics

Improving Scientific Document Retrieval with Academic Concept Index

Adapting general-domain retrievers to scientific domains is challenging due to the scarcity of large-scale domain-specific relevance annotations and the substantial mismatch in vocabulary and information needs. Recent approaches address these issues through two independent directions that leverage large language models (LLMs): (1) generating synthetic queries for fine-tuning, and (2) generating auxiliary contexts to support relevance matching. However, both directions overlook the diverse academic concepts embedded within scientific documents, often producing redundant or conceptually narrow queries and contexts. To address this limitation, we introduce an academic concept index, which extracts key concepts from papers and organizes them guided by an academic taxonomy. This structured index serves as a foundation for improving both directions. First, we enhance the synthetic query generation with concept coverage-based generation (CCQGen), which adaptively conditions LLMs on uncovered concepts to generate complementary queries with broader concept coverage. Second, we strengthen the context augmentation with concept-focused auxiliary contexts (CCExpand), which leverages a set of document snippets that serve as concise responses to the concept-aware CCQGen queries. Extensive experiments show that incorporating the academic concept index into both query generation and context augmentation leads to higher-quality queries, better conceptual alignment, and improved retrieval performance.

2601.00567

Jan 2026Information Retrieval

An Agentic Framework for Neuro-Symbolic Programming

Integrating symbolic constraints into deep learning models could make them more robust, interpretable, and data-efficient. Still, it remains a time-consuming and challenging task. Existing frameworks like DomiKnowS help this integration by providing a high-level declarative programming interface, but they still assume the user is proficient with the library's specific syntax. We propose AgenticDomiKnowS (ADS) to eliminate this dependency. ADS translates free-form task descriptions into a complete DomiKnowS program using an agentic workflow that creates and tests each DomiKnowS component separately. The workflow supports optional human-in-the-loop intervention, enabling users familiar with DomiKnowS to refine intermediate outputs. We show how ADS enables experienced DomiKnowS users and non-users to rapidly construct neuro-symbolic programs, reducing development time from hours to 10-15 minutes.

2601.00743

Jan 2026Artificial Intelligence

TeleWorld: Towards Dynamic Multimodal Synthesis with a 4D World Model

World models aim to endow AI systems with the ability to represent, generate, and interact with dynamic environments in a coherent and temporally consistent manner. While recent video generation models have demonstrated impressive visual quality, they remain limited in real-time interaction, long-horizon consistency, and persistent memory of dynamic scenes, hindering their evolution into practical world models. In this report, we present TeleWorld, a real-time multimodal 4D world modeling framework that unifies video generation, dynamic scene reconstruction, and long-term world memory within a closed-loop system. TeleWorld introduces a novel generation-reconstruction-guidance paradigm, where generated video streams are continuously reconstructed into a dynamic 4D spatio-temporal representation, which in turn guides subsequent generation to maintain spatial, temporal, and physical consistency. To support long-horizon generation with low latency, we employ an autoregressive diffusion-based video model enhanced with Macro-from-Micro Planning (MMPL)--a hierarchical planning method that reduces error accumulation from frame-level to segment-level-alongside efficient Distribution Matching Distillation (DMD), enabling real-time synthesis under practical computational budgets. Our approach achieves seamless integration of dynamic object modeling and static scene representation within a unified 4D framework, advancing world models toward practical, interactive, and computationally accessible systems. Extensive experiments demonstrate that TeleWorld achieves strong performance in both static and dynamic world understanding, long-term consistency, and real-time generation efficiency, positioning it as a practical step toward interactive, memory-enabled world models for multimodal generation and embodied intelligence.

2601.00051

Dec 2025Computer Vision

BHaRNet: Reliability-Aware Body-Hand Modality Expertized Networks for Fine-grained Skeleton Action Recognition

Skeleton-based human action recognition (HAR) has achieved remarkable progress with graph-based architectures. However, most existing methods remain body-centric, focusing on large-scale motions while neglecting subtle hand articulations that are crucial for fine-grained recognition. This work presents a probabilistic dual-stream framework that unifies reliability modeling and multi-modal integration, generalizing expertized learning under uncertainty across both intra-skeleton and cross-modal domains. The framework comprises three key components: (1) a calibration-free preprocessing pipeline that removes canonical-space transformations and learns directly from native coordinates; (2) a probabilistic Noisy-OR fusion that stabilizes reliability-aware dual-stream learning without requiring explicit confidence supervision; and (3) an intra- to cross-modal ensemble that couples four skeleton modalities (Joint, Bone, Joint Motion, and Bone Motion) to RGB representations, bridging structural and visual motion cues in a unified cross-modal formulation. Comprehensive evaluations across multiple benchmarks (NTU RGB+D~60/120, PKU-MMD, N-UCLA) and a newly defined hand-centric benchmark exhibit consistent improvements and robustness under noisy and heterogeneous conditions.

2601.00369

Jan 2026Computer Vision

$2+2=4$

Motivated by the observation that $2+2=4$, we consider four-dimensional $\mathcal{N}=2$ superconformal field theories on $S^2\timesΣ$, turning on a suitable rigid supergravity background. On the one hand, reduction of a four-dimensional theory ${T}$ on a Riemann surface $Σ$ leads to a family $\mathscr{F}[{T}, Σ]$ of two-dimensional $(2,2)$ unitary SCFTs, a two-dimensional analog of the four-dimensional theories of class $\mathscr{S}$. On the other hand, reduction on $S^2$ yields a non-unitary two-dimensional CFT $\mathscr{C}[{T}]$ whose chiral algebra is the same as the one associated to ${T}$ by the standard SCFT/VOA correspondence. This construction upgrades the vertex operator algebra to a full-fledged two-dimensional CFT. What's more, it leads to a novel 2d/2d correspondence, a "$2+2 = 4$" analog of the "$4+2=6$" AGT correspondence: the $S^2$ partition function of $\mathscr{F}[{T}; Σ]$ is computed by correlation functions of $\mathscr{C}[{T}]$ on $Σ$. The elliptic genus of $\mathscr{F}[{T}; Σ]$ is instead computed by a topological QFT $\mathscr{E}[T]$ on $Σ$. A central question is whether one can give a purely two-dimensional presentation of the family $\mathscr{F}[{T}; Σ]$ of $(2, 2)$ theories. We propose an algorithm to realize the $(2, 2)$ theories as gauged linear sigma models when ${T}$ is an Argyres-Douglas theory of type $(A_1, A_{2k})$ and $Σ$ an $n$-punctured sphere. We perform stringent checks of our conjecture for $k=1$ and $k=2$.

2601.00058

Dec 2025High Energy Physics - Theory

Large language models and the entropy of English

We use large language models (LLMs) to uncover long-ranged structure in English texts from a variety of sources. The conditional entropy or code length in many cases continues to decrease with context length at least to $N\sim 10^4$ characters, implying that there are direct dependencies or interactions across these distances. A corollary is that there are small but significant correlations between characters at these separations, as we show from the data independent of models. The distribution of code lengths reveals an emergent certainty about an increasing fraction of characters at large $N$. Over the course of model training, we observe different dynamics at long and short context lengths, suggesting that long-ranged structure is learned only gradually. Our results constrain efforts to build statistical physics models of LLMs or language itself.

2512.24969

Dec 2025Statistical Mechanics

End-to-End Test-Time Training for Long Context

We formulate long-context language modeling as a problem in continual learning rather than architecture design. Under this formulation, we only use a standard architecture -- a Transformer with sliding-window attention. However, our model continues learning at test time via next-token prediction on the given context, compressing the context it reads into its weights. In addition, we improve the model's initialization for learning at test time via meta-learning at training time. Overall, our method, a form of Test-Time Training (TTT), is End-to-End (E2E) both at test time (via next-token prediction) and training time (via meta-learning), in contrast to previous forms. We conduct extensive experiments with a focus on scaling properties. In particular, for 3B models trained with 164B tokens, our method (TTT-E2E) scales with context length in the same way as Transformer with full attention, while others, such as Mamba 2 and Gated DeltaNet, do not. However, similar to RNNs, TTT-E2E has constant inference latency regardless of context length, making it 2.7 times faster than full attention for 128K context. Our code is publicly available.

2512.23675

Dec 2025Machine Learning

SenseNova-MARS: Empowering Multimodal Agentic Reasoning and Search via Reinforcement Learning

While Vision-Language Models (VLMs) can solve complex tasks through agentic reasoning, their capabilities remain largely constrained to text-oriented chain-of-thought or isolated tool invocation. They fail to exhibit the human-like proficiency required to seamlessly interleave dynamic tool manipulation with continuous reasoning, particularly in knowledge-intensive and visually complex scenarios that demand coordinated external tools such as search and image cropping. In this work, we introduce SenseNova-MARS, a novel Multimodal Agentic Reasoning and Search framework that empowers VLMs with interleaved visual reasoning and tool-use capabilities via reinforcement learning (RL). Specifically, SenseNova-MARS dynamically integrates the image search, text search, and image crop tools to tackle fine-grained and knowledge-intensive visual understanding challenges. In the RL stage, we propose the Batch-Normalized Group Sequence Policy Optimization (BN-GSPO) algorithm to improve the training stability and advance the model's ability to invoke tools and reason effectively. To comprehensively evaluate the agentic VLMs on complex visual tasks, we introduce the HR-MMSearch benchmark, the first search-oriented benchmark composed of high-resolution images with knowledge-intensive and search-driven questions. Experiments demonstrate that SenseNova-MARS achieves state-of-the-art performance on open-source search and fine-grained image understanding benchmarks. Specifically, on search-oriented benchmarks, SenseNova-MARS-8B scores 67.84 on MMSearch and 41.64 on HR-MMSearch, surpassing proprietary models such as Gemini-3-Flash and GPT-5. SenseNova-MARS represents a promising step toward agentic VLMs by providing effective and robust tool-use capabilities. To facilitate further research in this field, we will release all code, models, and datasets.

2512.24330

Dec 2025Computer Vision

Pretraining Frame Preservation in Autoregressive Video Memory Compression

We present PFP, a neural network structure to compress long videos into short contexts, with an explicit pretraining objective to preserve the high-frequency details of single frames at arbitrary temporal positions. The baseline model can compress a 20-second video into a context at about 5k length, where random frames can be retrieved with perceptually preserved appearances. Such pretrained models can be directly fine-tuned as memory encoders for autoregressive video models, enabling long history memory with low context cost and relatively low fidelity loss. We evaluate the framework with ablative settings and discuss the trade-offs of possible neural architecture designs.

2512.23851

Dec 2025Computer Vision

The Illusion of Insight in Reasoning Models

Do reasoning models have "Aha!" moments? Prior work suggests that models like DeepSeek-R1-Zero undergo sudden mid-trace realizations that lead to accurate outputs, implying an intrinsic capacity for self-correction. Yet, it remains unclear whether such intrinsic shifts in reasoning strategy actually improve performance. Here, we study mid-reasoning shifts and instrument training runs to detect them. Our analysis spans 1M+ reasoning traces, hundreds of training checkpoints, three reasoning domains, and multiple decoding temperatures and model architectures. We find that reasoning shifts are rare, do not become more frequent with training, and seldom improve accuracy, indicating that they do not correspond to prior perceptions of model insight. However, their effect varies with model uncertainty. Building on this finding, we show that artificially triggering extrinsic shifts under high entropy reliably improves accuracy. Our results show that mid-reasoning shifts are symptoms of unstable inference behavior rather than an intrinsic mechanism for self-correction.

2601.00514

Jan 2026Artificial Intelligence

AMAP Agentic Planning Technical Report

We present STAgent, an agentic large language model tailored for spatio-temporal understanding, designed to solve complex tasks such as constrained point-of-interest discovery and itinerary planning. STAgent is a specialized model capable of interacting with ten distinct tools within spatio-temporal scenarios, enabling it to explore, verify, and refine intermediate steps during complex reasoning. Notably, STAgent effectively preserves its general capabilities. We empower STAgent with these capabilities through three key contributions: (1) a stable tool environment that supports over ten domain-specific tools, enabling asynchronous rollout and training; (2) a hierarchical data curation framework that identifies high-quality data like a needle in a haystack, curating high-quality queries with a filter ratio of 1:10,000, emphasizing both diversity and difficulty; and (3) a cascaded training recipe that starts with a seed SFT stage acting as a guardian to measure query difficulty, followed by a second SFT stage fine-tuned on queries with high certainty, and an ultimate RL stage that leverages data of low certainty. Initialized with Qwen3-30B-A3B to establish a strong SFT foundation and leverage insights into sample difficulty, STAgent yields promising performance on TravelBench while maintaining its general capabilities across a wide range of general benchmarks, thereby demonstrating the effectiveness of our proposed agentic model.

2512.24957

Dec 2025Artificial Intelligence

Categorical Reparameterization with Denoising Diffusion models

Gradient-based optimization with categorical variables typically relies on score-function estimators, which are unbiased but noisy, or on continuous relaxations that replace the discrete distribution with a smooth surrogate admitting a pathwise (reparameterized) gradient, at the cost of optimizing a biased, temperature-dependent objective. In this paper, we extend this family of relaxations by introducing a diffusion-based soft reparameterization for categorical distributions. For these distributions, the denoiser under a Gaussian noising process admits a closed form and can be computed efficiently, yielding a training-free diffusion sampler through which we can backpropagate. Our experiments show that the proposed reparameterization trick yields competitive or improved optimization performance on various benchmarks.

2601.00781

Jan 2026Machine Learning

2601.00605

Effective field theory for dissipative photons from higher-form symmetries

Recent developments in generalized symmetries have provided new insights into quantum field theories. Within this framework, photons can be understood as Nambu-Goldstone modes associated with a spontaneously broken higher-form symmetry. In this work, we develop an effective field theory that builds on this symmetry structure to describe the real-time dynamics of photons in insulating media at finite temperature. Combining the Schwinger-Keldysh formalism with the generalized coset construction, we formulate a symmetry-based effective action that incorporates both conservative and dissipative effects. The effective theory implements the dynamical Kubo-Martin-Schwinger symmetry, ensuring consistency with the fluctuation-dissipation relation and Onsager's reciprocal relations. Within this framework, we derive the entropy current associated with dissipative photon dynamics and demonstrate the non-negativity of its divergence, in accordance with the second law of thermodynamics. We also clarify the symmetry origin of the gauge redundancy in the unbroken phase within the Schwinger-Keldysh framework, relating it to strong and weak realizations of higher-form symmetries. Our results provide a model-independent effective description of photon dynamics in insulating media at finite temperature.

2601.00605

Jan 2026High Energy Physics - Theory

MorphAny3D: Unleashing the Power of Structured Latent in 3D Morphing

3D morphing remains challenging due to the difficulty of generating semantically consistent and temporally smooth deformations, especially across categories. We present MorphAny3D, a training-free framework that leverages Structured Latent (SLAT) representations for high-quality 3D morphing. Our key insight is that intelligently blending source and target SLAT features within the attention mechanisms of 3D generators naturally produces plausible morphing sequences. To this end, we introduce Morphing Cross-Attention (MCA), which fuses source and target information for structural coherence, and Temporal-Fused Self-Attention (TFSA), which enhances temporal consistency by incorporating features from preceding frames. An orientation correction strategy further mitigates the pose ambiguity within the morphing steps. Extensive experiments show that our method generates state-of-the-art morphing sequences, even for challenging cross-category cases. MorphAny3D further supports advanced applications such as decoupled morphing and 3D style transfer, and can be generalized to other SLAT-based generative models. Project page: https://xiaokunsun.github.io/MorphAny3D.github.io/.

2601.00204

Jan 2026Computer Vision

Dissecting the Hubble tension: Insights from a diverse set of Sound Horizon-free H0 measurements

The Hubble tension is commonly framed as a discrepancy between local, late-time measurements favoring $H_0 \approx 73$ km s$^{-1}$ Mpc$^{-1}$ and early-time, Sound-Horizon-based measurements favoring $H_0 \approx 67$ km s$^{-1}$ Mpc$^{-1}$. We challenge this viewpoint by analyzing 83 Sound-Horizon-independent $H_0$ measurements, categorized into four classes: Distance Ladder measurements using local calibrators; Local One-Step $Λ$CDM measurements assuming the standard expansion history; Pure Local One-Step measurements independent of $H(z)$ shape; and CMB Sound Horizon free measurements using CMB data without the Sound Horizon scale. We find that the 29 Distance Ladder measurements yield $H_0 = 72.74 \pm 0.40$ km s$^{-1}$ Mpc$^{-1}$ ($χ^2_ν\equiv χ^2/d.o.f= 0.74$), while the 54 One-Step measurements collectively yield $H_0 = 68.67 \pm 0.46$ km s$^{-1}$ Mpc$^{-1}$ ($χ^2_ν= 0.85$), a $6.7σ$ tension exceeding the Planck--SH0ES discrepancy. This tension remains significant at $4.5σ$ after accounting for correlations. Among One-Step categories, Local One-Step $Λ$CDM measurements favor the lowest value ($H_0 = 67.18 \pm 0.90$ km s$^{-1}$ Mpc$^{-1}$), Pure Local One-Step yield an intermediate value ($H_0 = 70.38 \pm 1.00$ km s$^{-1}$ Mpc$^{-1}$), and CMB Sound Horizon Free measurements give $H_0 = 68.71 \pm 0.63$ km s$^{-1}$ Mpc$^{-1}$. Thus, that the Hubble tension is better characterized as a discrepancy between the Distance Ladder and all other methodologies, rather than an early-vs-late-time split. We also identify a $2.4σ$ internal tension among One-Step measurements: analyses assuming $Λ$CDM systematically recover lower $H_0$ values by about 3.2 km s$^{-1}$ Mpc$^{-1}$ compared to model-independent methods. This suggests either unrecognized systematics/physics in the Distance Ladder or deviations from $Λ$CDM in the late-time Universe.

2601.00650

Jan 2026Cosmology and Nongalactic Astrophysics

AEGIS: Exploring the Limit of World Knowledge Capabilities for Unified Mulitmodal Models

The capability of Unified Multimodal Models (UMMs) to apply world knowledge across diverse tasks remains a critical, unresolved challenge. Existing benchmarks fall short, offering only siloed, single-task evaluations with limited diagnostic power. To bridge this gap, we propose AEGIS (\emph{i.e.}, \textbf{A}ssessing \textbf{E}diting, \textbf{G}eneration, \textbf{I}nterpretation-Understanding for \textbf{S}uper-intelligence), a comprehensive multi-task benchmark covering visual understanding, generation, editing, and interleaved generation. AEGIS comprises 1,050 challenging, manually-annotated questions spanning 21 topics (including STEM, humanities, daily life, etc.) and 6 reasoning types. To concretely evaluate the performance of UMMs in world knowledge scope without ambiguous metrics, we further propose Deterministic Checklist-based Evaluation (DCE), a protocol that replaces ambiguous prompt-based scoring with atomic ``Y/N'' judgments, to enhance evaluation reliability. Our extensive experiments reveal that most UMMs exhibit severe world knowledge deficits and that performance degrades significantly with complex reasoning. Additionally, simple plug-in reasoning modules can partially mitigate these vulnerabilities, highlighting a promising direction for future research. These results highlight the importance of world-knowledge-based reasoning as a critical frontier for UMMs.

2601.00561

Jan 2026Computer Vision

What Drives Success in Physical Planning with Joint-Embedding Predictive World Models?

A long-standing challenge in AI is to develop agents capable of solving a wide range of physical tasks and generalizing to new, unseen tasks and environments. A popular recent approach involves training a world model from state-action trajectories and subsequently use it with a planning algorithm to solve new tasks. Planning is commonly performed in the input space, but a recent family of methods has introduced planning algorithms that optimize in the learned representation space of the world model, with the promise that abstracting irrelevant details yields more efficient planning. In this work, we characterize models from this family as JEPA-WMs and investigate the technical choices that make algorithms from this class work. We propose a comprehensive study of several key components with the objective of finding the optimal approach within the family. We conducted experiments using both simulated environments and real-world robotic data, and studied how the model architecture, the training objective, and the planning algorithm affect planning success. We combine our findings to propose a model that outperforms two established baselines, DINO-WM and V-JEPA-2-AC, in both navigation and manipulation tasks. Code, data and checkpoints are available at https://github.com/facebookresearch/jepa-wms.

2512.24497

Dec 2025Artificial Intelligence

Qubits and Vacuum Amplitudes

High-energy colliders, such as the Large Hadron Collider (LHC) at CERN, are genuine quantum machines, so, in line with Richard Feynman's original motivation for Quantum Computing, the scattering processes that take place there are natural candidates to be simulated on a quantum system. Potential applications range from quantum machine learning methods for collider data analysis, to faster and more precise evaluations of intricate multiloop Feynman diagrams, more efficient jet clustering, improved simulations of parton showers, and many other tasks. In this work, the focus will be on two specific applications: first, the identification of the causal structure of multiloop vacuum amplitudes, a key ingredient of the Loop-Tree Duality and an area with deep connections to graph theory; and second, the integration and sampling of high-dimensional functions. The latter constitutes a first step toward the realization of a fully fledged quantum event generator operating at high perturbative orders.

2601.00722

Jan 2026High Energy Physics - Phenomenology

LLM Agents for Combinatorial Efficient Frontiers: Investment Portfolio Optimization

Investment portfolio optimization is a task conducted in all major financial institutions. The Cardinality Constrained Mean-Variance Portfolio Optimization (CCPO) problem formulation is ubiquitous for portfolio optimization. The challenge of this type of portfolio optimization, a mixed-integer quadratic programming (MIQP) problem, arises from the intractability of solutions from exact solvers, where heuristic algorithms are used to find approximate portfolio solutions. CCPO entails many laborious and complex workflows and also requires extensive effort pertaining to heuristic algorithm development, where the combination of pooled heuristic solutions results in improved efficient frontiers. Hence, common approaches are to develop many heuristic algorithms. Agentic frameworks emerge as a promising candidate for many problems within combinatorial optimization, as they have been shown to be equally efficient with regard to automating large workflows and have been shown to be excellent in terms of algorithm development, sometimes surpassing human-level performance. This study implements a novel agentic framework for the CCPO and explores several concrete architectures. In benchmark problems, the implemented agentic framework matches state-of-the-art algorithms. Furthermore, complex workflows and algorithm development efforts are alleviated, while in the worst case, lower but acceptable error is reported.

2601.00770

Jan 2026Computational Engineering, Finance, and Science

Diagnosing Critical Behavior in AdS Einstein-Maxwell-Scalar Theory via Holographic Entanglement Measures

We investigate the holographic mixed-state entanglement measures in the Einstein-Maxwell-Scalar (EMS) theory. Several quantities are computed, including the holographic entanglement entropy (HEE), mutual information (MI), entanglement wedge cross-section (EWCS), and butterfly velocity ($v_B$). Our findings demonstrate that these measures can effectively diagnose phase transitions. Notably, EWCS and MI, as mixed-state entanglement measures, exhibit behavior opposite to that of the HEE. Additionally, we study the butterfly velocity, a dynamic quantum information measure, and observe that it behaves differently from the static quantum information measures. We propose that the butterfly velocity is initially dominated by entanglement and subsequently by thermal entropy as the coupling constant increases. Moreover, we examine the scaling behavior of the holographic entanglement measures and find that all the critical exponents are equal to $1$, which is twice that of the scalar field. We also explore the inequality between EWCS and MI, noting that the growth rate of MI consistently exceeds that of EWCS during phase transitions. These features are expected to be universal across thermodynamic phase transitions, with the inequalities becoming more significant as one moves away from the critical point.

2601.00069

Dec 2025High Energy Physics - Theory

2512.25014

Diffusion Language Models are Provably Optimal Parallel Samplers

Diffusion language models (DLMs) have emerged as a promising alternative to autoregressive models for faster inference via parallel token generation. We provide a rigorous foundation for this advantage by formalizing a model of parallel sampling and showing that DLMs augmented with polynomial-length chain-of-thought (CoT) can simulate any parallel sampling algorithm using an optimal number of sequential steps. Consequently, whenever a target distribution can be generated using a small number of sequential steps, a DLM can be used to generate the distribution using the same number of optimal sequential steps. However, without the ability to modify previously revealed tokens, DLMs with CoT can still incur large intermediate footprints. We prove that enabling remasking (converting unmasked tokens to masks) or revision (converting unmasked tokens to other unmasked tokens) together with CoT further allows DLMs to simulate any parallel sampling algorithm with optimal space complexity. We further justify the advantage of revision by establishing a strict expressivity gap: DLMs with revision or remasking are strictly more expressive than those without. Our results not only provide a theoretical justification for the promise of DLMs as the most efficient parallel sampler, but also advocate for enabling revision in DLMs.

2512.25014

Dec 2025Machine Learning

(PhD Thesis) The Information Locally Stored in Quantum Fields: From Entanglement to Gravity

This is an updated version of my PhD thesis, defended at the University of Waterloo on the 2nd of April 2025, uploaded to the ArXiv with the goal of reaching a wider audience. The thesis is divided into 5 chapters, respectively containing (I) a brief introduction to local quantum field theory (QFT), (II) a description of local probes in QFT, (III) a discussion of entanglement in QFT and how to probe it, (IV) a description of the regimes where QFT interactions can be approximated by direct interactions, and (V) a discussion the information about the geometry of spacetime contained in quantum fields. The partial goal of this thesis is to serve as a guide for students aiming to tackle these different research programs. If the reader is interested in pursuing one or more research projects detailed here, they are encouraged to contact me for collaboration in these topics.

2601.00128

Dec 2025Quantum Physics

Improving Multi-step RAG with Hypergraph-based Memory for Long-Context Complex Relational Modeling

Multi-step retrieval-augmented generation (RAG) has become a widely adopted strategy for enhancing large language models (LLMs) on tasks that demand global comprehension and intensive reasoning. Many RAG systems incorporate a working memory module to consolidate retrieved information. However, existing memory designs function primarily as passive storage that accumulates isolated facts for the purpose of condensing the lengthy inputs and generating new sub-queries through deduction. This static nature overlooks the crucial high-order correlations among primitive facts, the compositions of which can often provide stronger guidance for subsequent steps. Therefore, their representational strength and impact on multi-step reasoning and knowledge evolution are limited, resulting in fragmented reasoning and weak global sense-making capacity in extended contexts. We introduce HGMem, a hypergraph-based memory mechanism that extends the concept of memory beyond simple storage into a dynamic, expressive structure for complex reasoning and global understanding. In our approach, memory is represented as a hypergraph whose hyperedges correspond to distinct memory units, enabling the progressive formation of higher-order interactions within memory. This mechanism connects facts and thoughts around the focal problem, evolving into an integrated and situated knowledge structure that provides strong propositions for deeper reasoning in subsequent steps. We evaluate HGMem on several challenging datasets designed for global sense-making. Extensive experiments and in-depth analyses show that our method consistently improves multi-step RAG and substantially outperforms strong baseline systems across diverse tasks.

2512.23959

Dec 2025Computation and Language

MotionPhysics: Learnable Motion Distillation for Text-Guided Simulation

Accurately simulating existing 3D objects and a wide variety of materials often demands expert knowledge and time-consuming physical parameter tuning to achieve the desired dynamic behavior. We introduce MotionPhysics, an end-to-end differentiable framework that infers plausible physical parameters from a user-provided natural language prompt for a chosen 3D scene of interest, removing the need for guidance from ground-truth trajectories or annotated videos. Our approach first utilizes a multimodal large language model to estimate material parameter values, which are constrained to lie within plausible ranges. We further propose a learnable motion distillation loss that extracts robust motion priors from pretrained video diffusion models while minimizing appearance and geometry inductive biases to guide the simulation. We evaluate MotionPhysics across more than thirty scenarios, including real-world, human-designed, and AI-generated 3D objects, spanning a wide range of materials such as elastic solids, metals, foams, sand, and both Newtonian and non-Newtonian fluids. We demonstrate that MotionPhysics produces visually realistic dynamic simulations guided by natural language, surpassing the state of the art while automatically determining physically plausible parameters. The code and project page are available at: https://wangmiaowei.github.io/MotionPhysics.github.io/.

2601.00504

Jan 2026Computer Vision

Retrieval--Reasoning Processes for Multi-hop Question Answering: A Four-Axis Design Framework and Empirical Trends

Multi-hop question answering (QA) requires systems to iteratively retrieve evidence and reason across multiple hops. While recent RAG and agentic methods report strong results, the underlying retrieval--reasoning \emph{process} is often left implicit, making procedural choices hard to compare across model families. This survey takes the execution procedure as the unit of analysis and introduces a four-axis framework covering (A) overall execution plan, (B) index structure, (C) next-step control (strategies and triggers), and (D) stop/continue criteria. Using this schema, we map representative multi-hop QA systems and synthesize reported ablations and tendencies on standard benchmarks (e.g., HotpotQA, 2WikiMultiHopQA, MuSiQue), highlighting recurring trade-offs among effectiveness, efficiency, and evidence faithfulness. We conclude with open challenges for retrieval--reasoning agents, including structure-aware planning, transferable control policies, and robust stopping under distribution shift.

2601.00536

Jan 2026Computation and Language

SafeMo: Linguistically Grounded Unlearning for Trustworthy Text-to-Motion Generation

Text-to-motion (T2M) generation with diffusion backbones achieves strong realism and alignment. Safety concerns in T2M methods have been raised in recent years; existing methods replace discrete VQ-VAE codebook entries to steer the model away from unsafe behaviors. However, discrete codebook replacement-based methods have two critical flaws: firstly, replacing codebook entries which are reused by benign prompts leads to drifts on everyday tasks, degrading the model's benign performance; secondly, discrete token-based methods introduce quantization and smoothness loss, resulting in artifacts and jerky transitions. Moreover, existing text-to-motion datasets naturally contain unsafe intents and corresponding motions, making them unsuitable for safety-driven machine learning. To address these challenges, we propose SafeMo, a trustworthy motion generative framework integrating Minimal Motion Unlearning (MMU), a two-stage machine unlearning strategy, enabling safe human motion generation in continuous space, preserving continuous kinematics without codebook loss and delivering strong safety-utility trade-offs compared to current baselines. Additionally, we present the first safe text-to-motion dataset SafeMoVAE-29K integrating rewritten safe text prompts and continuous refined motion for trustworthy human motion unlearning. Built upon DiP, SafeMo efficiently generates safe human motions with natural transitions. Experiments demonstrate effective unlearning performance of SafeMo by showing strengthened forgetting on unsafe prompts, reaching 2.5x and 14.4x higher forget-set FID on HumanML3D and Motion-X respectively, compared to the previous SOTA human motion unlearning method LCR, with benign performance on safe prompts being better or comparable. Code: https://github.com/AIGeeksGroup/SafeMo. Website: https://aigeeksgroup.github.io/SafeMo.

2601.00590

Jan 2026Computer Vision

Scaling Open-Ended Reasoning to Predict the Future

High-stakes decision making involves reasoning under uncertainty about the future. In this work, we train language models to make predictions on open-ended forecasting questions. To scale up training data, we synthesize novel forecasting questions from global events reported in daily news, using a fully automated, careful curation recipe. We train the Qwen3 thinking models on our dataset, OpenForesight. To prevent leakage of future information during training and evaluation, we use an offline news corpus, both for data generation and retrieval in our forecasting system. Guided by a small validation set, we show the benefits of retrieval, and an improved reward function for reinforcement learning (RL). Once we obtain our final forecasting system, we perform held-out testing between May to August 2025. Our specialized model, OpenForecaster 8B, matches much larger proprietary models, with our training improving the accuracy, calibration, and consistency of predictions. We find calibration improvements from forecasting training generalize across popular benchmarks. We open-source all our models, code, and data to make research on language model forecasting broadly accessible.

2512.25070

Dec 2025Machine Learning

RoboMIND 2.0: A Multimodal, Bimanual Mobile Manipulation Dataset for Generalizable Embodied Intelligence

While data-driven imitation learning has revolutionized robotic manipulation, current approaches remain constrained by the scarcity of large-scale, diverse real-world demonstrations. Consequently, the ability of existing models to generalize across long-horizon bimanual tasks and mobile manipulation in unstructured environments remains limited. To bridge this gap, we present RoboMIND 2.0, a comprehensive real-world dataset comprising over 310K dual-arm manipulation trajectories collected across six distinct robot embodiments and 739 complex tasks. Crucially, to support research in contact-rich and spatially extended tasks, the dataset incorporates 12K tactile-enhanced episodes and 20K mobile manipulation trajectories. Complementing this physical data, we construct high-fidelity digital twins of our real-world environments, releasing an additional 20K-trajectory simulated dataset to facilitate robust sim-to-real transfer. To fully exploit the potential of RoboMIND 2.0, we propose MIND-2 system, a hierarchical dual-system frame-work optimized via offline reinforcement learning. MIND-2 integrates a high-level semantic planner (MIND-2-VLM) to decompose abstract natural language instructions into grounded subgoals, coupled with a low-level Vision-Language-Action executor (MIND-2-VLA), which generates precise, proprioception-aware motor actions.

2512.24653

Dec 2025Robotics

All-in-One Video Restoration under Smoothly Evolving Unknown Weather Degradations

All-in-one image restoration aims to recover clean images from diverse unknown degradations using a single model. But extending this task to videos faces unique challenges. Existing approaches primarily focus on frame-wise degradation variation, overlooking the temporal continuity that naturally exists in real-world degradation processes. In practice, degradation types and intensities evolve smoothly over time, and multiple degradations may coexist or transition gradually. In this paper, we introduce the Smoothly Evolving Unknown Degradations (SEUD) scenario, where both the active degradation set and degradation intensity change continuously over time. To support this scenario, we design a flexible synthesis pipeline that generates temporally coherent videos with single, compound, and evolving degradations. To address the challenges in the SEUD scenario, we propose an all-in-One Recurrent Conditional and Adaptive prompting Network (ORCANet). First, a Coarse Intensity Estimation Dehazing (CIED) module estimates haze intensity using physical priors and provides coarse dehazed features as initialization. Second, a Flow Prompt Generation (FPG) module extracts degradation features. FPG generates both static prompts that capture segment-level degradation types and dynamic prompts that adapt to frame-level intensity variations. Furthermore, a label-aware supervision mechanism improves the discriminability of static prompt representations under different degradations. Extensive experiments show that ORCANet achieves superior restoration quality, temporal consistency, and robustness over image and video-based baselines. Code is available at https://github.com/Friskknight/ORCANet-SEUD.

2601.00533

Jan 2026Computer Vision

Geometry of Reason: Spectral Signatures of Valid Mathematical Reasoning

We present a training-free method for detecting valid mathematical reasoning in large language models through spectral analysis of attention patterns. By treating attention matrices as adjacency matrices of dynamic graphs over tokens, we extract four interpretable spectral diagnostics, the Fiedler value (algebraic connectivity), high-frequency energy ratio (HFER), graph signal smoothness, and spectral entropy, that exhibit statistically significant differences between valid and invalid mathematical proofs. Experiments across seven transformer models from four independent architectural families (Meta Llama, Alibaba Qwen, Microsoft Phi, and Mistral AI) demonstrate that this spectral signature produces effect sizes up to Cohen's $d = 3.30$ ($p < 10^{-116}$), enabling 85.0--95.6\% classification accuracy under rigorous evaluation, with calibrated thresholds reaching 93--95\% on the full dataset. The method requires no training data, fine-tuning, or learned classifiers: a single threshold on a spectral metric suffices for high accuracy. Through systematic label correction, we discover that the spectral method detects logical coherence rather than compiler acceptance, identifying mathematically valid proofs that formal verifiers reject due to technical failures. We further identify an architectural dependency: Mistral-7B's Sliding Window Attention shifts the discriminative signal from HFER to late-layer Smoothness ($d = 2.09$, $p_{\text{MW}} = 1.16 \times 10^{-48}$), revealing that attention mechanism design affects which spectral features capture reasoning validity. These findings establish spectral graph analysis as a principled framework for reasoning verification with immediate applications to hallucination detection and AI safety monitoring.

2601.00791

Jan 2026Machine Learning

Trending Today

Browse by Field

Machine Learning

3 arXiv categories

Neural networks, deep learning, statistical learning, and optimization methods

cs.LGstat.MLcs.NE

Artificial Intelligence

2 arXiv categories

Knowledge representation, reasoning, planning, and multi-agent systems

cs.AIcs.MA

Natural Language Processing

1 arXiv category

Language models, text understanding, machine translation, and speech

cs.CL

Computer Vision

1 arXiv category

Image recognition, object detection, video understanding, and 3D vision

cs.CV

Computer Graphics

2 arXiv categories

Rendering, simulation, computational geometry, and visual effects

cs.GRcs.CG

Robotics

2 arXiv categories

Robot perception, control, manipulation, and autonomous systems

cs.ROeess.SY

Systems & Networking

5 arXiv categories

Distributed systems, databases, networking, operating systems, and performance

cs.DCcs.NIcs.OS+2 more

Security & Cryptography

1 arXiv category

Cryptography, network security, privacy, and secure systems

cs.CR

Theory & Algorithms

5 arXiv categories

Computational complexity, data structures, algorithms, and game theory

cs.CCcs.DScs.GT+2 more

Programming Languages

2 arXiv categories

Language design, compilers, program analysis, and software engineering

cs.PLcs.SE

Human-Computer Interaction

3 arXiv categories

User interfaces, interaction design, accessibility, and social computing

cs.HCcs.CYcs.SI

Information Retrieval

1 arXiv category

Search engines, recommender systems, and web mining

cs.IR

Popular Categories

Machine Learning Artificial Intelligence Computer Vision Computation and Language Robotics Cryptography and Security Analysis of PDEs Combinatorics Cosmology and Nongalactic Astrophysics High Energy Physics - Theory

Highly Cited

Page 1

Explore Papers

Trending Today

mHC: Manifold-Constrained Hyper-Connections

Recursive Language Models

Fast-weight Product Key Memory

Nested Learning: The Illusion of Deep Learning Architectures

Deep Delta Learning

RoboReward: General-Purpose Vision-Language Reward Models for Robotics

Dynamic Large Concept Models: Latent Reasoning in an Adaptive Semantic Space

Avatar Forcing: Real-Time Interactive Head Avatar Generation for Natural Conversation

NeoVerse: Enhancing 4D World Model with in-the-wild Monocular Videos

IRPO: Scaling the Bradley-Terry Model via Reinforcement Learning

AdaGaR: Adaptive Gabor Representation for Dynamic Scene Reconstruction

Let It Flow: Agentic Crafting on Rock and Roll, Building the ROME Model within an Open Agentic Learning Ecosystem

Youtu-LLM: Unlocking the Native Agentic Potential for Lightweight Large Language Models

Training AI Co-Scientists Using Rubric Rewards

DiffThinker: Towards Generative Multimodal Reasoning with Diffusion Models

Pixel-to-4D: Camera-Controlled Image-to-Video Generation with Dynamic 3D Gaussians

OpenOneRec Technical Report

Evaluating Parameter Efficient Methods for RLVR

Youtu-Agent: Scaling Agent Productivity with Automated Generation and Hybrid Policy Optimization

Dream2Flow: Bridging Video Generation and Open-World Manipulation with 3D Object Flow

Improving Scientific Document Retrieval with Academic Concept Index

An Agentic Framework for Neuro-Symbolic Programming

TeleWorld: Towards Dynamic Multimodal Synthesis with a 4D World Model

BHaRNet: Reliability-Aware Body-Hand Modality Expertized Networks for Fine-grained Skeleton Action Recognition

$2+2=4$

Large language models and the entropy of English

End-to-End Test-Time Training for Long Context

SenseNova-MARS: Empowering Multimodal Agentic Reasoning and Search via Reinforcement Learning

Pretraining Frame Preservation in Autoregressive Video Memory Compression

The Illusion of Insight in Reasoning Models

AMAP Agentic Planning Technical Report

Categorical Reparameterization with Denoising Diffusion models

Effective field theory for dissipative photons from higher-form symmetries

MorphAny3D: Unleashing the Power of Structured Latent in 3D Morphing

Dissecting the Hubble tension: Insights from a diverse set of Sound Horizon-free H0 measurements

AEGIS: Exploring the Limit of World Knowledge Capabilities for Unified Mulitmodal Models

What Drives Success in Physical Planning with Joint-Embedding Predictive World Models?

Qubits and Vacuum Amplitudes

LLM Agents for Combinatorial Efficient Frontiers: Investment Portfolio Optimization

Diagnosing Critical Behavior in AdS Einstein-Maxwell-Scalar Theory via Holographic Entanglement Measures

Diffusion Language Models are Provably Optimal Parallel Samplers

(PhD Thesis) The Information Locally Stored in Quantum Fields: From Entanglement to Gravity

Improving Multi-step RAG with Hypergraph-based Memory for Long-Context Complex Relational Modeling

MotionPhysics: Learnable Motion Distillation for Text-Guided Simulation

Retrieval--Reasoning Processes for Multi-hop Question Answering: A Four-Axis Design Framework and Empirical Trends

SafeMo: Linguistically Grounded Unlearning for Trustworthy Text-to-Motion Generation

Scaling Open-Ended Reasoning to Predict the Future

RoboMIND 2.0: A Multimodal, Bimanual Mobile Manipulation Dataset for Generalizable Embodied Intelligence

All-in-One Video Restoration under Smoothly Evolving Unknown Weather Degradations

Geometry of Reason: Spectral Signatures of Valid Mathematical Reasoning

Trending Today

Browse by Field

Computer Science

Machine Learning

Artificial Intelligence

Natural Language Processing

Computer Vision

Computer Graphics

Robotics

Systems & Networking

Security & Cryptography

Theory & Algorithms

Programming Languages

Human-Computer Interaction

Information Retrieval

Mathematics

Physics

Statistics

Quantitative Biology

Economics

Quantitative Finance

Electrical Engineering and Systems Science

Popular Categories

Highly Cited

Highly Cited

Trending Today

mHC: Manifold-Constrained Hyper-Connections

Recursive Language Models