Probability & Statistics
Probability theory, stochastic processes, and mathematical statistics
Probability theory, stochastic processes, and mathematical statistics
 2601.04161
2601.04161We study the Ergodic Properties of Random Walks in stationary ergodic environments without uniform ellipticity under a minimal assumption. There are two main components in our work. The first step is to adopt the arguments of Lawler to first prove a uniqueness principle. We use a more general definition of environments using~\textit{Environment Functions}. As a corollary, we can deduce an invariance principle under these assumptions for balanced environments under some assumptions. We also use the uniqueness principle to show that any balanced, elliptic random walk must have the same transience behaviour as the simple symmetric random walk. The second is to transfer the results we deduce in balanced environments to general ergodic environments(under some assumptions) using a control technique to derive a measure under which the \textit{local process} is stationary and ergodic. As a consequence of our results, we deduce the Law of Large Numbers for the Random Walk and an Invariance Principle under our assumptions.
 2601.04079
2601.04079We study the total variation distance under two information-erasing maps on inhomogeneous Bernoulli product measures: summation and homogenization. While summation is a Markov kernel and hence satisfies the usual data processing inequality, homogenization -- which maps each Bernoulli parameter to the cumulative mean -- is not. Nevertheless, we prove that the homogenization map also reduces the TV distance, up to a universal constant. The argument is based on an explicit two-sided control of the TV distance between Poisson binomials, obtained via a parameter interpolation and a second-moment extraction lemma.
 2601.04038
2601.04038The class of generalized gamma convolutions (GGC) is closed with respect to (wrt) change of scales, weak limits and addition and multiplication of independent random variables. Our main result adds the new property that GGC is also closed wrt q-th powers, q>1. The proof uses explicit formulas for the densities of finite sums of independent gamma variables, hyperbolically completely monotone functions (HCM) and the Laplace transform. The result is applied to sums and products of independent gamma variables and to symmetric extended GGC (symEGGC).
Many classical objects of study related to the geometry/topology of smooth Gaussian fields (e.g. the volume, surface area or Euler characteristic of excursion sets) have a `locality' property which is crucial to their analysis. More recently, progress has been made in studying `non-local' quantities of such fields (e.g. the component/nodal count or the Betti numbers of excursion sets). In this work we establish limit theorems for non-local, approximately additive functionals of stationary fields evaluated on growing domains. Specifically we show that, for weakly dependent fields, such functionals satisfy a law of large numbers, have variance which is asymptotic to the volume of the domain and satisfy both quantitative and almost-sure central limit theorems. Our approach uses a covariance formula for topological events to establish a form of quasi-association for the functionals.
 2601.03920
2601.03920This paper investigates the nonparametric estimation of a heteroskedastic variance function on the sphere in a regression framework, assuming the variance belongs to a Besov regularity class. A needlet-based estimator is proposed, combining multiresolution analysis with hard thresholding. The method exploits the spatial and spectral localization of needlets to adapt to unknown smoothness and is shown to attain minimax-optimal convergence rates over Besov spaces.
 2601.03911
2601.03911This paper establishes the theoretical foundations for the asymptotic separability of Gaussian Mixture Models (GMMs) in high dimensions by extending the classical Feldman-Hájek theorem. We first prove that a countable mixture of Gaussian measures is a well-defined probability measure. Our primary result, the Gaussian Mixture Dichotomy Theorem, demonstrates that the mutual singularity of individual Gaussian components is a sufficient condition for the mutual singularity of the resulting mixtures. We provide a rigorous proof and further discuss the ``Mixed Case,'' where the presence of even a single equivalent pair of components leads to partial absolute continuity via the Lebesgue decomposition, thereby defining the theoretical limits of perfect classification in infinite-dimensional spaces.
 2601.03900
2601.03900The classical Mazur-Ulam theorem establishes that every surjective isometry between normed real vector spaces is an affine transformation. In various applied mathematical settings, however, one encounters maps that preserve distances not pointwise, but almost everywhere with respect to a probability measure. This paper provides a rigorous generalization of the Mazur-Ulam theorem to probability spaces. We prove that if a measurable map on a subset of Rd preserves distances almost everywhere with respect to a measure with full-dimensional support, it coincides almost everywhere with a global Euclidean isometry, defined as an orthogonal transformation followed by a translation.
 2601.03866
2601.03866In this note we consider $2$-dimensional lattice random walks killed at leaving a wedge with opening $α\in(0,π]$. Assuming that the walk cannot jump over the boundary of the wedge we prove that there exists a harmonic polynomial if and only if $α=π/m$ with some integer $m$. Our proof is constructive and allows one to give exact expressions for harmonic polynomials for every integer $m$. Furthermore, we give exact expressions for all finite moments of the exit time, this result is valid for all angles $α$.
 2601.03864
2601.03864We prove a refined version of the Aldous and Brown's exponential approximation of stationary hitting times. These are valid for all reversible Markov chains. We then specialise our estimates for vertex-transitive graphs, where we obtain improved bounds which depend on the growth of the graphs. The most delicate cases are when the diameter is comparable to that of low-dimensional tori. In particular, in "dimensions" less than four (up to logarithmic factors) our error terms are the square of those of Aldous and Brown. These improved bounds play a crucial role in the companion work arXiv:2202.02255 characterising the fluctuations of the cover time on vertex-transitive graphs.
 2601.03719
2601.03719We develop a Bayesian nonparametric framework for inference in spatio-temporal Hawkes processes, extending existing theoretical results beyond the purely temporal setting. Our framework encompasses modelling both the background and triggering components of the Hawkes process through Gaussian Processes priors. Under appropriate smoothness and regularity assumptions on the true parameter and the nonparametric prior family, we derive explicit posterior contraction rates for the conditional intensity function and the model's parameter, in the asymptotic regime of repeatedly observed and independent sequences. Our analysis generalizes known contraction results for purely temporal Hawkes processes to the spatio-temporal setting, which allows to jointly model self-excitation across time and space in event data. These results provide, to our knowledge, the first theoretical guarantees for Bayesian nonparametric methods in spatio-temporal point data.
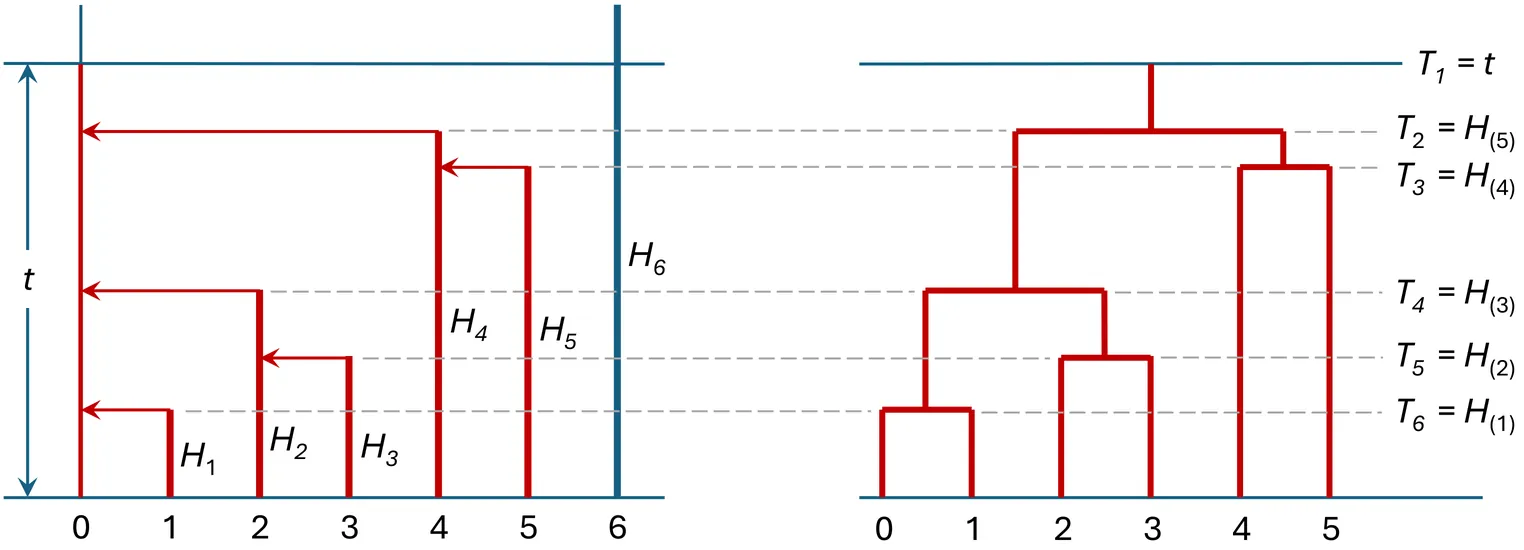
The Feller diffusion is studied as the limit of a coalescent point process in which the density of the node height distribution is skewed towards zero. Using a unified approach, a number of recent results pertaining to scaling limits of branching processes are reinterpreted as properties of the Feller diffusion arising from this limit. The notion of Bernoulli sampling of a finite population is extended to the diffusion limit to cover finite Poisson-distributed samples drawn from infinite continuum populations. We show that the coalescent tree of a Poisson-sampled Feller diffusion corresponds to a coalescent point process with a node height distribution taking the same algebraic form as that of a Bernoulli-sampled birth-death process. By adapting methods for analysing k-sampled birth-death processes, in which the sample size is pre-specified, we develop methods for studying the coalescent properties of the k-sampled Feller diffusion.
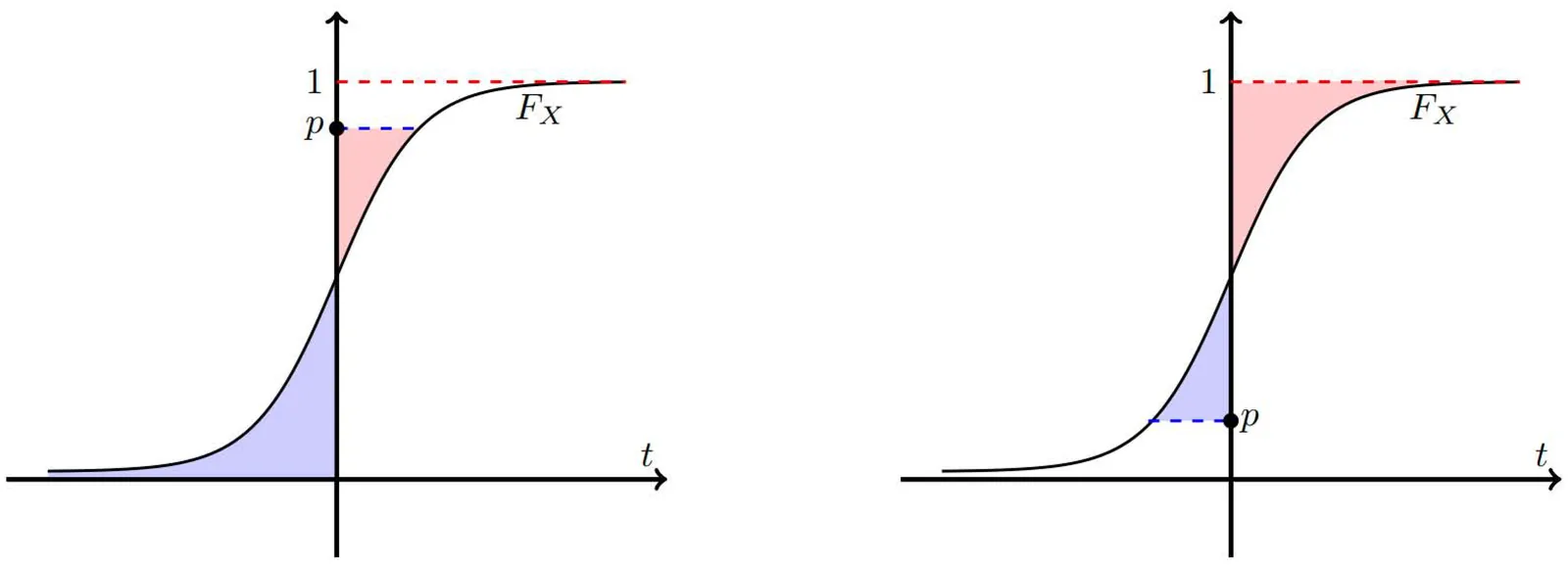
Stochastic dominance has been studied extensively, particularly in the finance and economics literature. In this paper, we obtain two results. First, necessary conditions for higher-order inverse stochastic dominance are developed. These conditions, which involve moment inequalities of the minimum order statistics, are analogous to the ones obtained by Fishburn (1980b) for usual higher-order stochastic dominance. Second, we investigate how background risk variables influence usual higher-order stochastic dominance. The main result generalizes the ones in Pomatto et al. (2020) from the first-order and second-order stochastic dominance to the higher-order.

We present a universal concentration bound for sums of random variables under arbitrary dependence, and we prove it is asymptotically optimal for every fixed common marginal law. The concentration bound is a direct - yet previously unnoticed - consequence of the subadditivity of expected shortfall, a property well known to financial statisticians. The sharpness result is a significant contribution relying on the construction of worst-case dependency profiles between identically distributed random variables.
 2601.03411
2601.03411We show that Activated Random Walk on $\mathbb{Z}$ is explosive above criticality. That is, activating a single particle in a supercritical state of sleeping particles triggers an infinite avalanche of activity with positive probability. This extends the same result recently proven by Brown, Hoffman, and Son for i.i.d. initial distributions to the setting of ergodic ones, thus completing the proof of a conjecture of Rolla's in dimension one. As a corollary we obtain that, for supercritical ergodic initial distributions with any positive density of particles initially active, the system will stay active almost surely. Our result is another piece of evidence attesting to the universality of the phase transition of Activated Random Walk on $\mathbb{Z}$.
 2601.03384
2601.03384We establish bounds on the mixing times of conjugacy-invariant random walks on finite nilpotent groups in terms of the mixing times of their projections onto the abelianization. This comparison framework shows that, in several natural cases of interest, the mixing behavior on a nilpotent group is governed by that of the projected walk on the abelianization, reducing the study of mixing to a simpler problem in the Abelian setting. As an application, these bounds yield cutoff for two examples of conjugacy-invariant walks on unit upper-triangular matrix groups previously studied by Arias-Castro, Diaconis, and Stanley (2004) and by Nestoridi (2019).
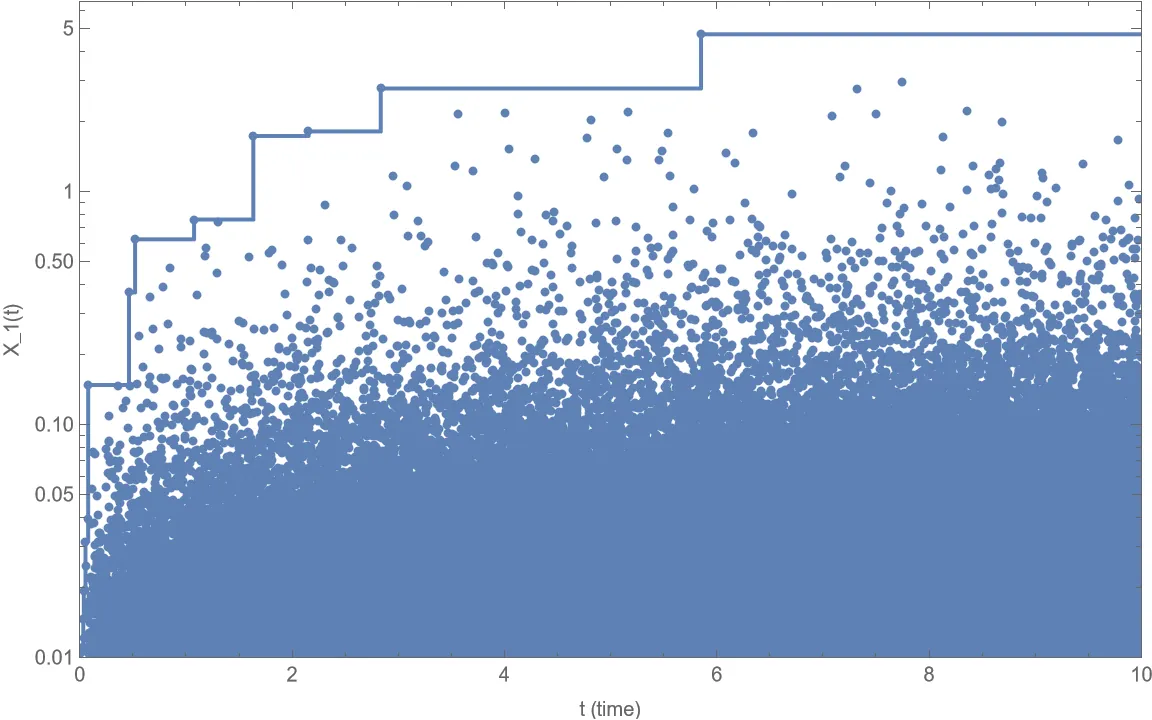
Motivated by a connection to the infinite Ginibre point process, decoupled random walks were introduced in a recent article Alsmeyer, Iksanov and Kabluchko (2025). The decoupled random walk is a sequence of independent random variables, in which the $n$th variable has the same distribution as the position at time $n$ of a standard random walk with nonnegative increments. We prove distributional convergence in the Skorokhod space equipped with the $J_1$-topology of the running maxima and the first passage times of decoupled random walks. We show that there exist five different regimes, in which distinct limit theorems arise. Rather different functional limit theorems for the number of visits of decoupled standard random walk to the interval $[0,t]$ as $t\to\infty$ were earlier obtained in the aforementioned paper Alsmeyer, Iksanov and Kabluchko (2025). While the limit processes for the first passage times are inverse extremal-like processes, the limit processes for the number of visits are stationary Gaussian.
 2601.03064
2601.03064We study an entropy functional $H_K$ that is sensitive to a prescribed similarity structure on a state space. For finite spaces, $H_K$ coincides with the order-1 similarity-sensitive entropy of Leinster and Cobbold. We work in the general measure-theoretic setting of kernelled probability spaces $(Ω,μ,K)$ introduced by Leinster and Roff, and develop basic structural properties of $H_K$. Our main results concern the behavior of $H_K$ under coarse-graining. For a measurable map $f:Ω\to Y$ and input law $μ$, we define a law-induced kernel on $Y$ whose pullback minimally dominates $K$, and show that it yields a coarse-graining inequality and a data-processing inequality for $H_K$, for both deterministic maps and general Markov kernels. We also introduce conditional similarity-sensitive entropy and an associated mutual information, and compare their behavior to the classical Shannon case.
 2601.03006
2601.03006In this paper, we study backward stochastic differential equations driven by G-Brownian motion where the generator has time-varying monotonicity with respect to y and Lipsitz property with respect to z. Through the Yosida approximation, we have proved the existence and uniqueness of the solutions to these equations.
 2601.02992
2601.02992Lawler and Trujillo Ferreras constructed a well-known coupling between the Brownian loop soups in $\mathbb{R}^2$ and the random walk loop soups on $\mathbb{Z}^2$ (one rescales the random walk loops by $1/N$, their time parametrizations by $1/(2N^2)$, and let $N\to \infty$), which led to numerous applications. It nevertheless only holds for loops with time length at least $N^{θ-2}$ for $θ\in(2/3,2)$. In particular, there is no control on mesoscopic loops with time length less than $N^{-4/3}$ (i.e.\ roughly diameter less than $N^{-2/3}$). In this paper, we find a simple way to remove the restriction $θ>2/3$, so that such a coupling works for all $θ\in (0,2)$, i.e. for loops at all polynomial scales. We also establish this coupling in any dimension $d\ge 1$ (i.e. for random walk loop soups on $\mathbb{Z}^d$ and Brownian loop soups on $\mathbb{R}^d$).
 2601.02935
2601.02935In this article, we prove that, on the diffusive time scale, condensing zero-range processes converge to a dimension-decaying diffusion process on the simplex \[ Σ= \{(x_1,\dots,x_S) : x_i \ge 0,\; \sum_{i\in S} x_i = 1\}, \] where $S$ is a finite set. This limiting diffusion has the distinctive feature of being absorbed at the boundary of the simplex. More precisely, once the process reaches a face \[ Σ_A = \{(x_1,\dots,x_S) : x_i \ge 0,\; \sum_{i\in A} x_i = 1\}, \qquad A \subset S, \] it remains confined to this set and evolves in the corresponding lower-dimensional simplex according to a new diffusion whose parameters depend on the subset $A$. This mechanism repeats itself, leading to successive reductions of the dimension, until one of the vertices of the simplex is reached in finite time. At that point, the process becomes permanently trapped. The proof relies on a method to extend the domain of the associated martingale problem, which may be of independent interest and useful in other contexts.