Complex Variables
Holomorphic functions, automorphic group actions and forms, pseudoconvexity, complex geometry, analytic spaces, analytic sheaves.
Holomorphic functions, automorphic group actions and forms, pseudoconvexity, complex geometry, analytic spaces, analytic sheaves.

Milnor's fibration theorem and its generalizations play a central role in the study of singularities of complex and real analytic maps. In the complex analytic case, the Milnor fibration on the sphere is always given by the normalized map $f/|f|$. In contrast, for real analytic maps the existence of such a normalized Milnor fibration generally fails, even when a Milnor--Le fibration exists on a tube. For locally surjective real analytic maps $f:(R^n,0)->(R^k,0)$ with isolated critical value, the existence of a Milnor--Le fibration on a tube is guaranteed under a transversality condition. However, the associated fibration on the sphere need not be given by the normalized map $f/||f||$, unless an additional regularity condition (d-regularity) is imposed. In this paper we show that this apparent obstruction is not intrinsic. More precisely, we prove that for any such map satisfying the transversality property, there exists a homeomorphism $h:(R^k,0)->(R^k,0)$ of the target space such that the composition $h^{-1}f$ becomes d-regular. As a consequence, the normalized map $(h^{-1}f)/||h^{-1}f||$ defines a smooth locally trivial fibration on the sphere, which is equivalent to both the Milnor--Le fibration on the tube and the Milnor fibration on the sphere. Our result reveals a closer topological parallel between real and complex analytic singularities than previously recognized, without changing the topological type of the singularity.
 2601.03529
2601.03529In this paper we establish duality theorems relating Bott-Chern and Aeppli cohomology, both with and without compact support, on non-compact complex manifolds under suitable pseudoconvexity assumptions. In particular, on Stein manifolds we obtain a full Bott-Chern-Aeppli duality extending Serre duality for Dolbeault cohomology. We also show that these results fail in general without pseudoconvexity assumptions by constructing explicit counterexamples on non-compact complex surfaces.
 2601.02768
2601.02768In this paper, we determine the automorphism groups of generalized Kausz compactifications $\mathcal T_{s,p,n}$. By establishing the (semi-)positivity of the anticanonical bundles of $\mathcal T_{s,p,n}$, we also determine the automorphism groups of generalized spaces of complete collineations $\mathcal M_{s,p,n}$. The results in this paper are partially taken from the author's earlier arxiv post (Canonical blow-ups of grassmann manifolds, arxiv:2007.06200).
 2601.01474
2601.01474We recently characterized the separated determinantal point processes $Λ_φ$ associated with Fock spaces $\mathcal F_φ$ in the plane with doubling weight $φ$. We also showed that, as expected, a more restrictive condition is required to characterize the separated Poisson processes with the same first intensities as $Λ_φ$. To gain further insight into this different behavior, we center our attention to radial weights $φ(z)$ and introduce a hybrid process $Λ_φ^M=\{r_k e^{iθ_k}\}_{k=1}^\infty$, where the moduli $r_k$ are taken from $Λ_φ$, while the arguments $θ_k$ are chosen independently and uniformly in $[0,2π)$. Our main result is that $Λ_φ^M$ is almost surely separated if and only if its first intensity satisfies the same condition as in the Poisson case.
 2601.01396
2601.01396The present paper studies the existence of valuative interpolation on the local ring of an irreducible analytic subvariety at singular points. We firstly develop the concepts and methods of Zhou weights and Tian functions near singular points of irreducible analytic subvarieties. By applying these tools, we establish the necessary and sufficient conditions for the existence of valuative interpolations on the rings of germs of holomorphic functions and weakly holomorphic functions at a singular point. As applications, we characterize the existence of valuative interpolations on the quotient ring of the ring of convergent power series in real variables. We also present separated necessary and sufficient conditions for the existence of valuative interpolations on the quotient ring of polynomial rings with complex coefficients and real coefficients. Furthermore, we show that the conditions become both necessary and sufficient under certain conditions on the zero set of the given polynomials.
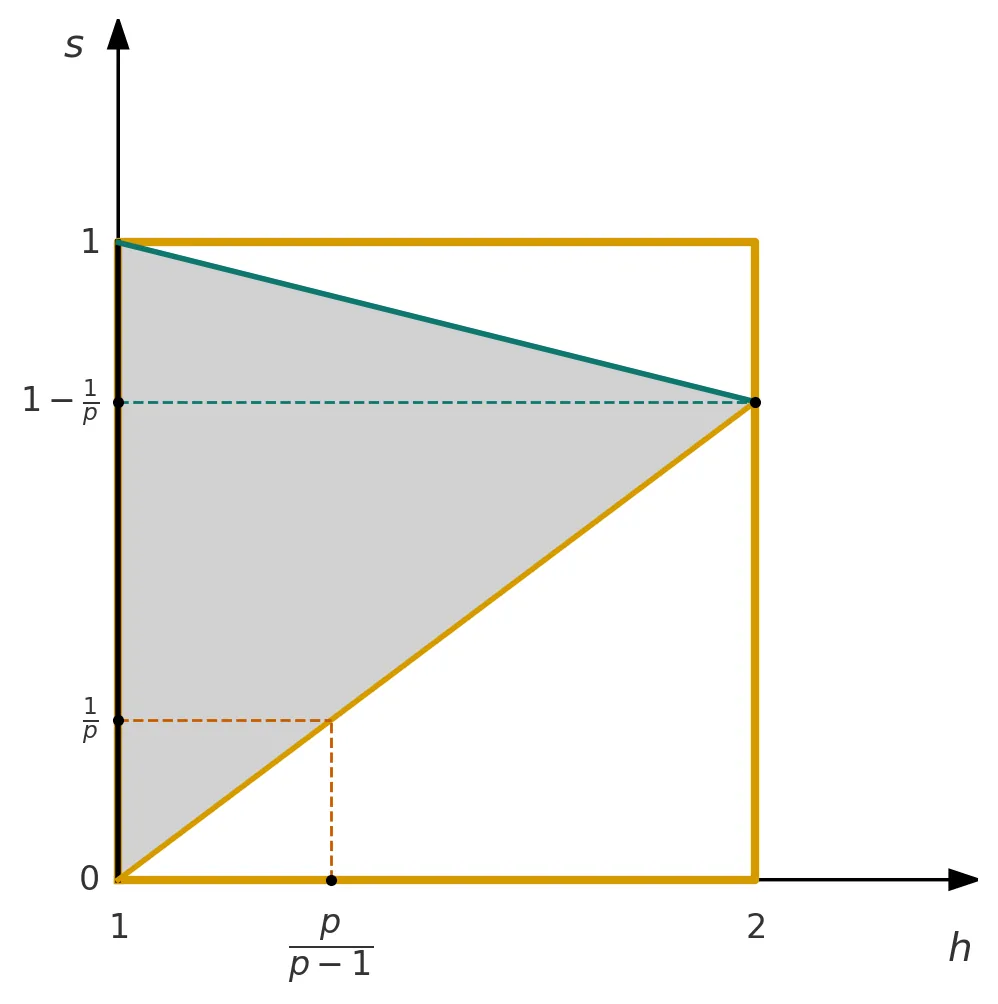
Let $Γ$ be a bounded Jordan curve and $Ω_i,Ω_e$ its two complementary components. For $1<p<\infty,\,s\in(0,1)$ we define $\mathcal{B}_{p,p}^s(Ω_{i,e})$ as the set of functions $f:Γ\to \mathbb C$ having harmonic extension $u$ respectively in $Ω_i$ and $Ω_e$ such that $$ \iint_{Ω_{i,e}} |\nabla u(z)|^p d(z,Γ)^{(1-s)p-1} dxdy<+\infty.$$ If $Γ$ is further assumed to be rectifiable we define $B_{p,p}^s(Γ)$ as the space of functions $f\in L^p(Γ)$ such that $$\iint_{Γ\times Γ}\frac{|f(z)-f(ζ)|^p}{|z-ζ|^{1+ps}} |dz||dζ|<+\infty.$$ When $Γ$ is the unit circle these three spaces coincide with the homogeneous fractional Besov-Sobolev space. For a general rectifiable curve these spaces need not coincide and our first goal is to investigate the cases of equality: while the chord-arc property is the necessary and sufficient condition for equality in the classical case of $s=1/p,\, p\ge 2$, this is no longer the case for general $s\in (0,1)$. We show however that equality holds for radial-Lipschitz curves. In the general (possibly non-rectifiable) case we study boundary values of functions in $\mathcal{B}_{p,p}^s(Ω_{i,e})$ and give conditions for equality of these trace-spaces that we then call $\mathcal{B}^s_{p,p}(Γ)$. Using Plemelj-Calderón property we further identify $\mathcal{B}^s_{p,p}(Γ)$ with the space of restrictions of a weighted Sobolev space of the plane. Finally we re-interpretate some of our results as the "almost"-Dirichlet principle in the spirit of Maz'ya.
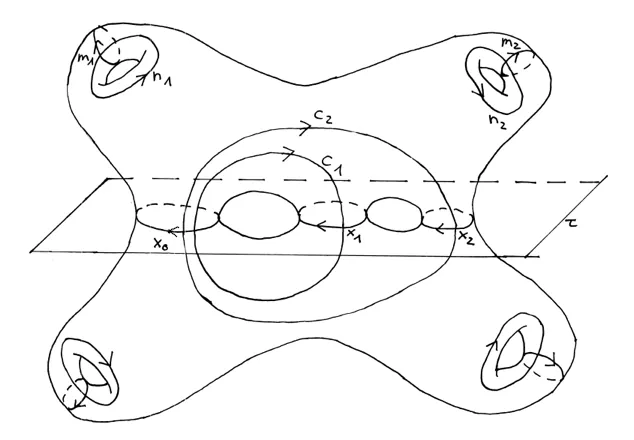
This paper develops a discrete theory of real Riemann surfaces based on quadrilateral cellular decompositions (quad-graphs) and a linear discretization of the Cauchy-Riemann equations. We construct a discrete analogue of an antiholomorphic involution and classify the topological types of discrete real Riemann surfaces, recovering the classical results on the number of real ovals and the separation of the surface. Central to our approach is the construction of a symplectic homology basis adapted to the discrete involution. Using this basis, we prove that the discrete period matrix admits the same canonical decomposition $Π= \frac{1}{2} H + i T$ as in the smooth setting, where $H$ encodes the topological type and $T$ is purely imaginary. This structural result bridges the gap between combinatorial models and the classical theory of real algebraic curves.
 2512.19284
2512.19284We investigate deformation properties of balanced hyperbolicity, with particular emphasis on degenerate balanced manifolds and their behavior under modifications. In this context, we introduce two new notions of hyperbolicity for compact non-Kähler manifolds $X$ of complex dimension $\dim_{\mathbb{C}}X=n$ in degree $1 \leq p \leq n-1$, inspired by the work of F. Haggui and S. Marouani on $p$-Kähler hyperbolicity. The first notion, called \emph{p-SKT hyperbolicity}, generalizes the notions of SKT hyperbolicity and Gauduchon hyperbolicity introduced by S. Marouani. The second notion, called \emph{p-HS hyperbolicity}, extends the notion of sG hyperbolicity defined by Y. Ma. We investigate the relationship between these notions of analytic nature and their geometric counterparts, namely Kobayashi hyperbolicity and \emph{p-cyclic hyperbolicity} for $2 \leq p \leq n-1$, and we examine the openness under holomorphic deformations of both $p$-HS hyperbolicity and $p$-Kähler hyperbolicity.
 2512.18106
2512.18106We study reciprocity laws involving complex line bundles on fibrations in oriented circles. In particularly, we prove the following reciprocity law. Let $B$ be a complex manifold and $π_i : M_i \to B$ be a fibration in oriented circles, where $i$ runs through a finite set. Let $L_i$ and $N_i$ be complex line bundles on every $M_i$. The reciprocity law states that the sum of all $(π_i)_* \left(c_1(L_i) \cup c_1(N_i) \right)$, where $(π_i)_*$ is the Gysin map and $c_1$ is the first Chern class, equals zero in $H^3(B, {\mathbb Z})$ when the disjoint union of all $M_i$ is embedded into a holomorphic family of compact Riemann surfaces over the base $B$ such that in every fiber of this family the disjoint union of the embedded circles is the boundary of an embedded compact Riemann surface with boundary, and all $L_i$ and all $N_i$ are restrictions of holomorphic line bundles on this family.
 2512.16506
2512.16506We study the distribution kernel of a Toeplitz operator associated with a classical pseudodifferential operator on a compact, embeddable, strictly pseudoconvex CR manifold. The main result consists of a formula for the values at the diagonal of the second coefficient in the expansion of the symbol of the kernel. We also establish asymptotic expansions for Toeplitz operators on the positive part of a compact not necessary strictly pseudoconvex CR orbifold under certain natural assumptions.
 2512.15193
2512.15193In this paper, we consider weighted Bergman spaces $\mathcal{B}_{α,p}$ of log-subharmonic functions on the unit sphere. Using the isoperimetric inequality for the spherical metric we prove certain monotonicity property for super-level sets of $|f(x)|^p\mathcal{W}_n^α(x),$ where $f\in \mathcal{B}_{α,p}$ and $\mathcal{W}_n^α(x)$ is the Bergman weight. As a consequence, we solve a maximization problem for certain Wehrl-type (convex) functionals and concentration estimates. Moreover, we show the stability of these estimates, proving that near-extremizing values are achieved for near-extremizing functions.
 2512.11640
2512.11640We study the structure of the spectrum of the algebra of uniformly continuous holomorphic functions on the unit ball of $\ell_p$. Our main focus is the relationship between \emph{Gleason parts} and \emph{fibers}. For every $z \in B_{\ell_p}$ with $1 < p < \infty$, we prove that the fiber over $z$ contains $2^{\mathfrak{c}}$ distinct Gleason parts. We also investigate some of the properties of these Gleason parts and show the existence of many strong boundary points in certain fibers. We then examine the case $p = 1$, where similar results on the abundance of Gleason parts within the fibers hold, although the arguments required are more involved. Our results extend and complete earlier work on the subject, providing answers to previously posed questions.
 2512.11523
2512.11523Given a big and semipositive line bundle in the adjoint setting, we show that Donaldson's quantized Monge-Ampere energy associated with any bounded plurisubharmonic weight converges to the Monge-Ampere energy. Our proof refines an argument of Berman and Freixas i Montplet in the ample case by employing a pointwise semiclassical Ohsawa-Takegoshi type extension theorem. As an application, we obtain the weak convergence of adjoint Bergman measures associated with bounded plurisubharmonic weights toward the corresponding non-pluripolar measures.
 2512.11349
2512.11349We solve the commutant lifting and interpolation problems in the setting of the Hardy space and Schur functions on the open unit ball of $\mathbb{C}^n$. Our solutions also signify the role of inner functions on the unit ball, objects whose existence was once in doubt and to which Aleksandrov, Rudin, and others made fundamental contributions. Some of our results, particularly those related to inner functions, are new even in the classical, one-variable case.
 2512.10852
2512.10852We obtain the asymptotic behavior of hole probability for random holomorphic sections on a compact Riemann surface with respect to the hole size.
 2512.10528
2512.10528Given a measure $μ$ on the unit sphere $\partial\mathbb{B}^d$ in $\mathbb{C}^d$ with Lebesgue decomposition ${\rm d} μ= w \, {\rm d} σ+ {\rm d} μ_s$, with respect to the rotation-invariant Lebesgue measure $σ$ on $\partial \mathbb{B}^d$, we introduce notions of orthogonal polynomials $(\varphi_α)_{α\in \mathbb{N}_0^d}$, Verblunsky coefficients $(γ_{α,β})_{α,β\in \mathbb{N}_0^d}$, and an associated Christoffel function $λ_{\infty}^{(d)}(z; {\rm d} μ)$, and we prove a recurrence relation for the orthogonal polynomials involving the Verblunsky coefficients reminiscent of the classical Szegő recurrences, as well as an analogue of Verblunsky's theorem. Moreover, we establish a number of equalities involving the orthogonal polynomials, determinants of moment matrices, and the Christoffel function, and show that if ${\rm supp}\, μ_s$ is discrete, then the aforementioned quantities depend only on the absolutely continuous part of $μ$. If, in addition to ${\rm supp}\, μ_s$ being discrete, one is able to find $f \in H^{\infty}(\mathbb{B}^d)$ such that $f(0) = 1$ and $$\int_{\partial \mathbb{B}^d} |f(ζ)|^2 w(ζ) {\rm d}σ(ζ) \leq \exp\left( \int_{\partial \mathbb{B}^d} \log(w(ζ)) \, {\rm d}σ(ζ) \right),$$ then we establish a $d$-variate Szegő-Verblunsky theorem, namely $$\prod_{α\in \mathbb{N}_0^d} (1 - | γ_{0,α} |^2) = \exp\left(\int_{\partial\mathbb{B}^d} \log( w(ζ)) \, {\rm d}σ(ζ)\right).$$ Finally, we identify several classes of weights where one may construct such an $f$ and highlight an explicit example of a weight $w$, residing outside of these classes, where $\prod_{α\in \mathbb{N}_0^d} (1 - |γ_{0,α} |^2) \neq \exp\left(\int_{\partial\mathbb{B}^d} \log( w(ζ)) \, {\rm d}σ(ζ)\right)$.
 2512.10466
2512.10466We extend several geometric quantization results to the setting of big line bundles. More precisely, we prove the asymptotic isometry property for the map that associates to a metric on a big line bundle the corresponding sup-norms on the spaces of holomorphic sections of its tensor powers. Building on this, we show that submultiplicative norms on section rings of big line bundles are asymptotically equivalent to sup-norms. As an application, we show that any bounded submultiplicative filtration on the section ring of a big line bundle naturally gives rise to a Mabuchi geodesic ray, and the speed of this ray encodes the statistical invariants of the filtration.
 2512.07098
2512.07098In this paper, we show that for a broad class of pseudoconvex formal-analytic arithmetic surfaces over $\text{Spec}(\mathbb{Z})$, those which admit a nonconstant monic such regular function, that a conjecture of Bost-Charles that the ring of regular functions has continuum cardinality is implied by a purely complex-analytic conjecture. Under the conjecture, a Fekete-Szego-type approximation argument produces a polynomial "large" relative to the regular function, which in turn yields continuum many distinct regular functions. We also introduce a formula for the pushforward by a holomorphic function of the equilibrium Green's functions for our bordered Riemann surface with boundary, a formula which has constant term related to Arakelov degree.
 2512.05892
2512.05892We consider each of the three classes of representations of cyclic groups that arise in the study of rational sphere maps. We study the possible number of terms for invariant polynomials with non-negative coefficients that are constant on the appropriate line or hyperplane. Our result provides crucial information about gaps in the possible target dimensions for certain invariant polynomial sphere maps. We interpret our results in terms of sparseness for solutions of certain linear systems.
 2512.04379
2512.04379We investigate properties of ($α,β$)-harmonic functions. First, we discuss the the coefficient estimates for ($α,β$)-harmonic functions. In particular, we obtain Heinz's inequality for ($α,β$)-harmonic functions, propose a coefficient bound for normalized univalent ($α,β$)-harmonic functions and prove that this holds for the subclass that consists of starlike functions. Furthermore, by utilizing the relationship between ($α,β$)-harmonic functions and harmonic functions, we obtain Radó's theorem, Koebe type covering theorems and area theorem. Finally, we show growth estimates and distortion estimates for ($α,β$)-harmonic functions by using the $L^p$ norms of the boundary functions.