Trending in Physics
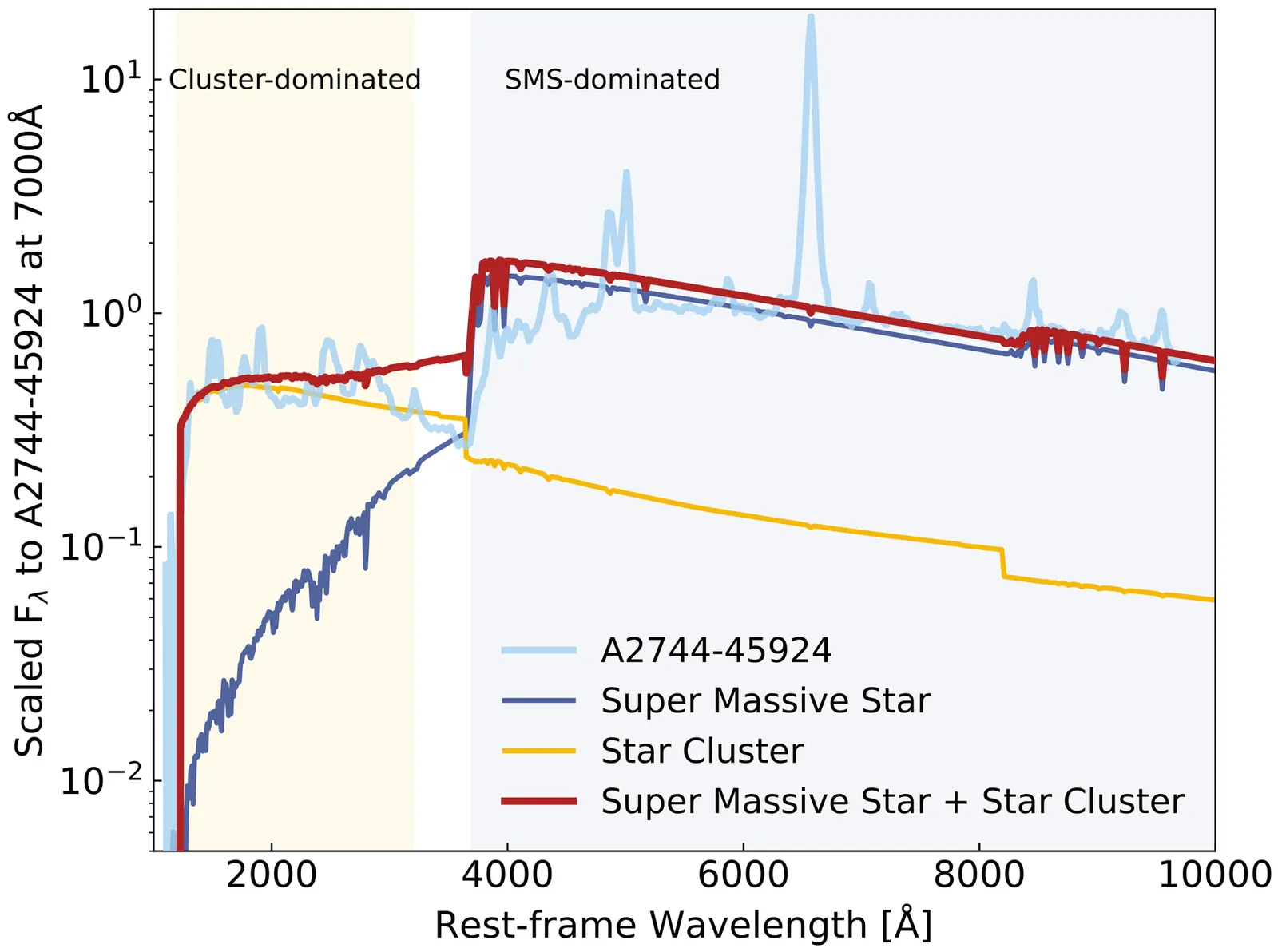
Little Red Dots as Globular Clusters in Formation
Little Red Dots (LRDs), among the most enigmatic high-redshift discoveries by JWST, are commonly believed to be powered by accreting supermassive black holes. Here, we explore the possibility that these sources are globular clusters in formation, with rest-frame UV arising from a very young stellar population and rest-frame optical from a short-lived supermassive ($>10^4$ M$_\odot$) star. The spectral profiles of LRDs are broadly consistent with this scenario, though the observed temperatures and bolometric luminosities favor emission reprocessed by optically thick, continuum-driven winds not fully captured by current models. The LRD $z\sim5-7$ UV luminosity function naturally evolves, under standard evolutionary and mass-loss prescriptions, into a present-day mass function with a turnover at $\log_{10}(M_\ast$/$M_\odot)=5.3$ and an exponential cutoff at high masses, consistent with local globular-cluster populations. We estimate the total present-day number density of LRDs formed across all redshifts to be $\approx0.3$ Mpc$^{-3}$, similar to local globular clusters. The observed LRD redshift range matches the age distribution of metal-poor globular clusters, without current LRD counterparts to the metal-rich population. If LRDs are globular clusters in formation, we predict chemical abundance patterns characteristic of multiple stellar populations, including enhanced He and N, and potential Na-O and Al-Mg anti-correlations. These results offer a local perspective to explore this surprisingly abundant population of distant sources, and a potential new window into extreme stellar astrophysics in the early Universe.
2602.15935
Feb 2026Astrophysics of Galaxies
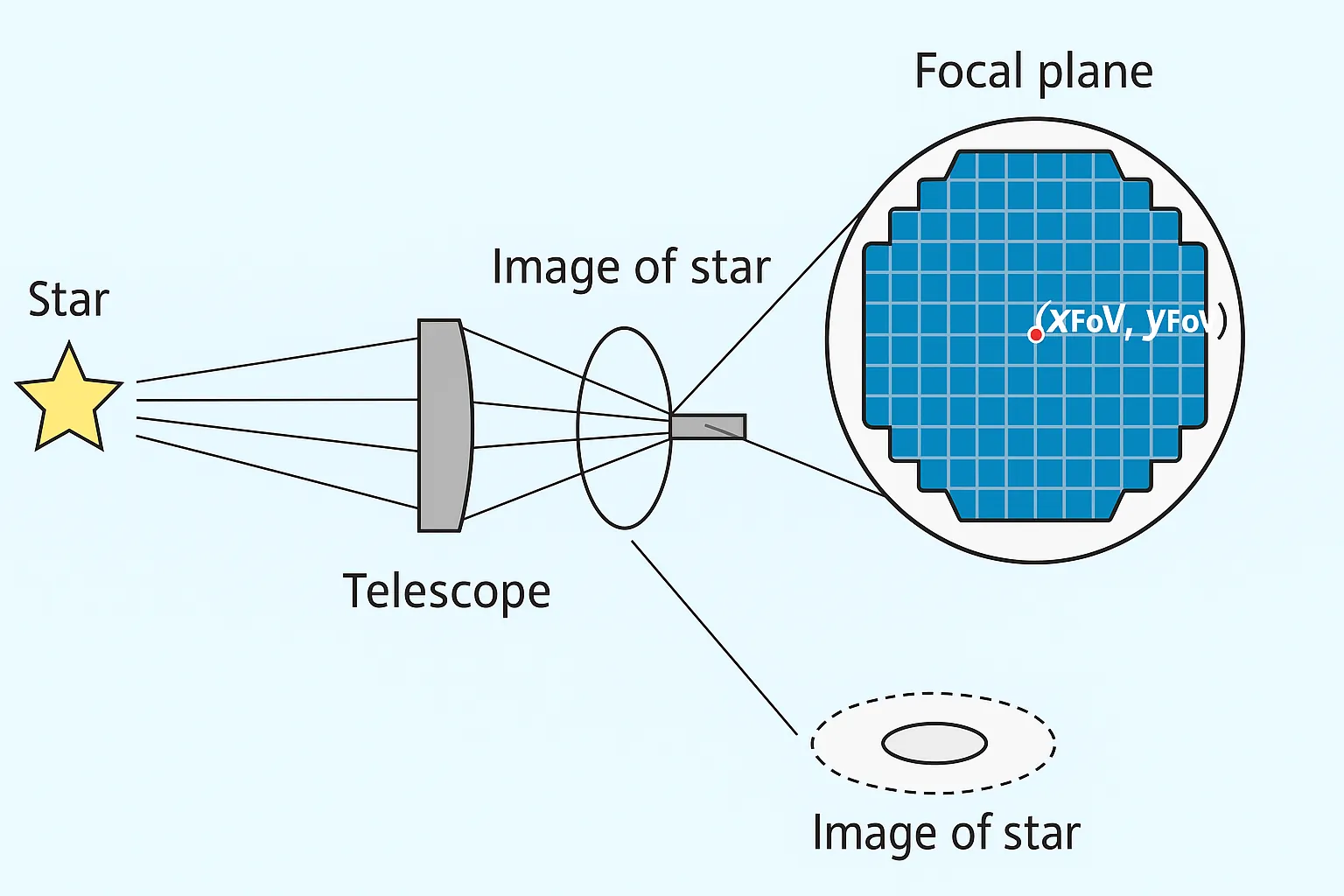
Deep Learning for Point Spread Function Modeling in Cosmology
We present the development of a data-driven, AI-based model of the Point Spread Function (PSF) that achieves higher accuracy than the current state-of-the-art approach, "PSF in the Full Field-of-View'' (PIFF). PIFF is widely used in leading weak-lensing surveys, including the Dark Energy Survey (DES), the Hyper Suprime-Cam (HSC) Survey, and the Vera C. Rubin Observatory Legacy Survey of Space and Time (LSST). The PSF characterizes how a point source, such as a star, is imaged after its light traverses the atmosphere and telescope optics, effectively representing the "blurred fingerprint'' of the entire imaging system. Accurate PSF modeling is essential for weak gravitational lensing analyses, as biases in its estimation propagate directly into cosmic shear measurements -- one of the primary cosmological probes of the expansion history of the Universe and the growth of large-scale structure for dark energy studies. To address the limitations of PIFF, which constructs PSF models independently for each CCD and therefore loses spatial coherence across the focal plane, we introduce a deep-learning-based framework for PSF reconstruction. In this approach, an autoencoder is trained on stellar images obtained with the Hyper Suprime-Cam (HSC) of the Subaru Telescope and combined with a Gaussian process to interpolate the PSF across the telescope's full field of view. This hybrid model captures systematic variations across the focal plane and achieves a reconstruction error of $3.4 \times 10^{-6}$ compared to PIFF's $3.7 \times 10^{-6}$, laying the foundation for integration into the LSST Science Pipelines.
2602.15780
Feb 2026Instrumentation and Methods for Astrophysics
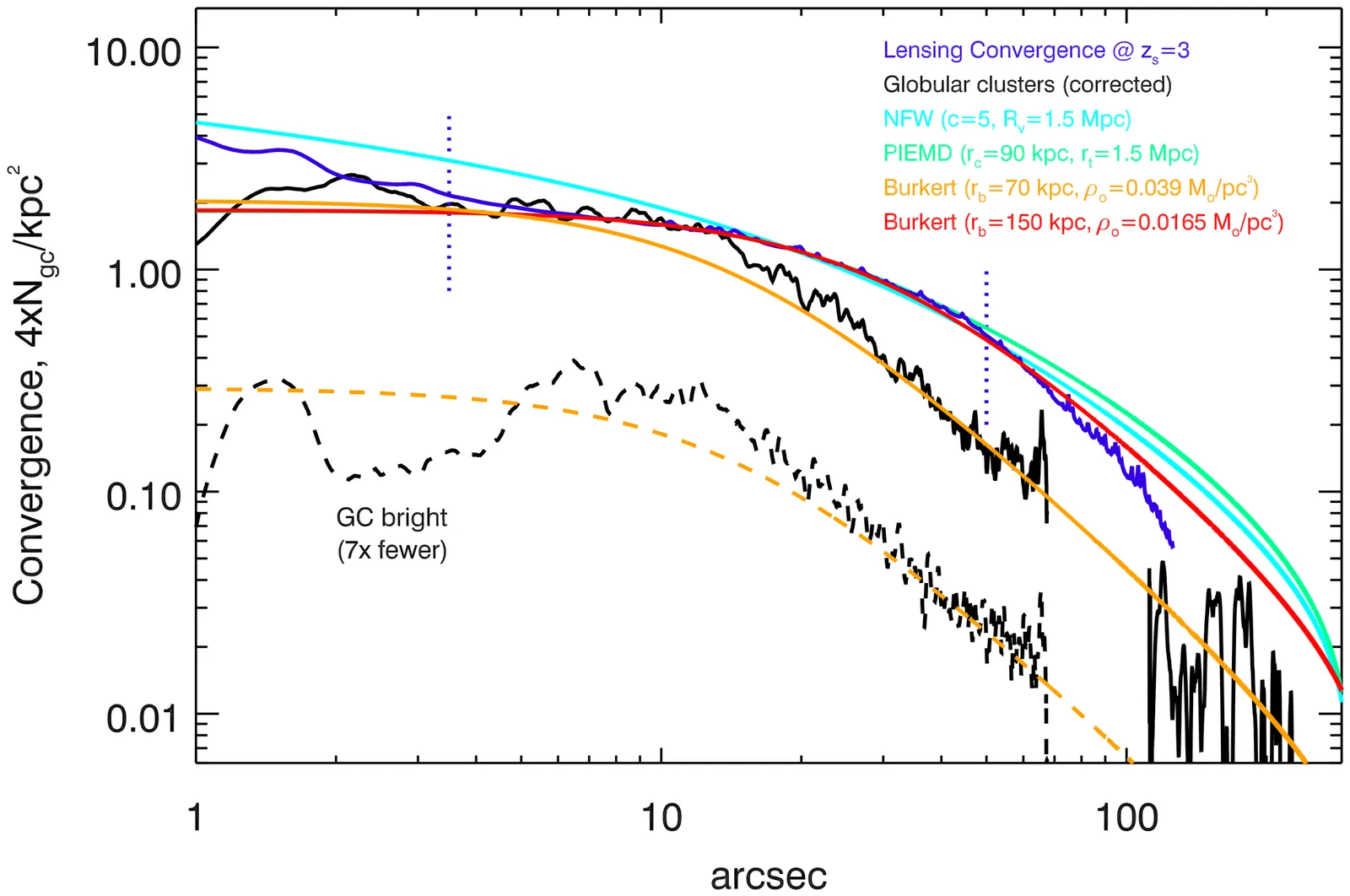
The large cores of dark matter and globular clusters in AS1063. Possible evidence of self-interacting dark matter. Or not
Deep JWST images of AS1063 reveals tens of thousands of globular clusters in the galaxy cluster AS1063. When compared with the lensing model based on the same JWST data, the distribution of globular clusters traces closely the distribution of lensing mass (mostly composed of dark matter). Interestingly, both the distributions of dark matter and globular clusters have large central cores. However the size of the core in the distribution of globular clusters is about half the size the core of the dark matter distribution. We argue that the standard cold dark matter and fuzzy dark matter models struggle to explain these large cores. Meanwhile, the self interacting dark matter with a velocity dependent cross section, combined with core stalling, offers a natural explanation to the existence of these cores if $σ_{\rm SI}\approx 0.3$ cm$^2$ g$^{-1}$ for galaxy cluster halos. But we also discuss how the lack of hydrodynamical N-body simulations capable of resolving globular clusters in galaxy cluster scale halos, hinders the possibility of ruling out the standard non-collisional dark matter scenario. Future high-resolution hydrodynamical simulations of galaxy clusters, with several trillion particles, and containing over a hundred thousand globular clusters, can provide the insight needed to transform the epistemic nature of dark matter into an ontological one
2602.15940
Feb 2026Astrophysics of Galaxies
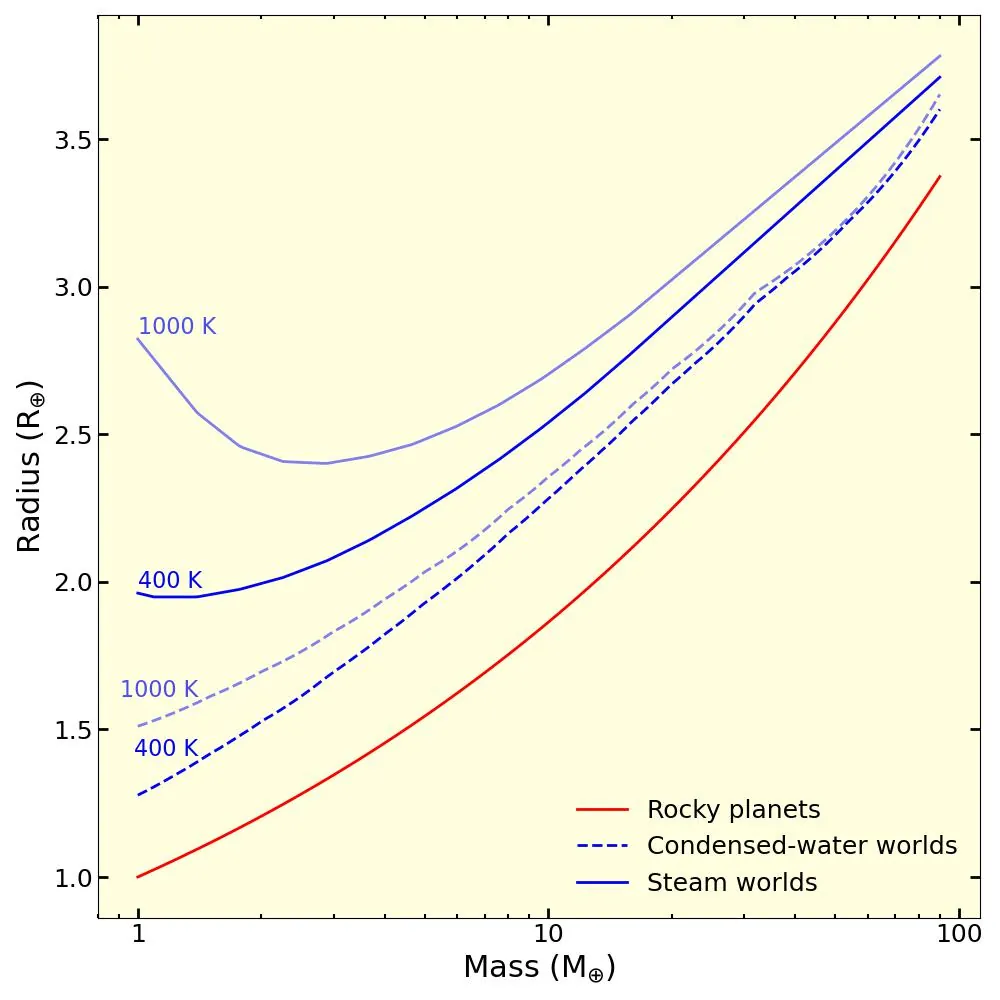
The Radius Cliff is a Waterfall: Explaining Sub-Neptune Exoplanets with Steam Worlds
The demographics of Kepler planets provide a key testbed for models of planet formation and evolution, particularly for explaining the radius valley separating super-Earths and sub-Neptunes. A primordial interpretation based on differences in bulk densities -- where rocky and water-rich planets form via migration pathways -- offers an alternative to atmospheric loss scenarios. Updated interior structure models of water worlds with adiabatic steam atmospheres reproduce the observed valley near $\sim2~R_\oplus$ more accurately. Furthermore, migration models from our Genesis library suggest that these formation pathways can also account for the distinct period distributions of super-Earths and sub-Neptunes, as well as the emergence of the hot Neptune desert. Motivated by this, we develop a Bayesian hierarchical mixture model for close-in Kepler planets ($P<100$ days), combining rocky planets and water worlds without H/He envelopes. The inferred mass distributions of rocky and water-rich planets peak at $\sim2.6~M_\oplus$ and $\sim7~M_\oplus$, respectively, with the water mass fraction of water worlds peaking at $\sim41\%$. Water worlds provide a good representation of the Kepler sub-Neptune population, with the radius cliff emerging as a ``waterfall" -- a sharp decline in their occurrence. However, our mass-radius analysis shows that water worlds alone cannot explain planets with $R \gtrsim 3~R_\oplus$, implying that at least $\sim20\%$ of sub-Neptunes in the sample are enriched in H/He gas.
2602.11923
Feb 2026Earth and Planetary Astrophysics
 2602.05973
2602.05973Does Cosmology require Hermiticity in Quantum Mechanics?
We explore the consequences of allowing non-Hermitian structures in quantum cosmology by extending the Wheeler DeWitt framework beyond strictly Hermitian dynamics. Using a controlled semiclassical reduction, we show how anti Hermitian contributions propagate into both early universe primordial fluctuations and late-time structure growth as effective damping or gain terms. Confronting this framework with inflationary observables, growth of structure and the observed near flatness of the universe, we derive strong infrared constraints that suppress non Hermiticity across cosmic history. We demonstrate that these bounds are mutually consistent between early and late-time probes and can be partially relaxed in theories beyond General Relativity. Our results establish cosmology as a novel arena for testing foundational aspects of quantum mechanics and suggest that Hermiticity may emerge dynamically along the semiclassical branch describing our universe.
2602.05973
Feb 2026Cosmology and Nongalactic Astrophysics
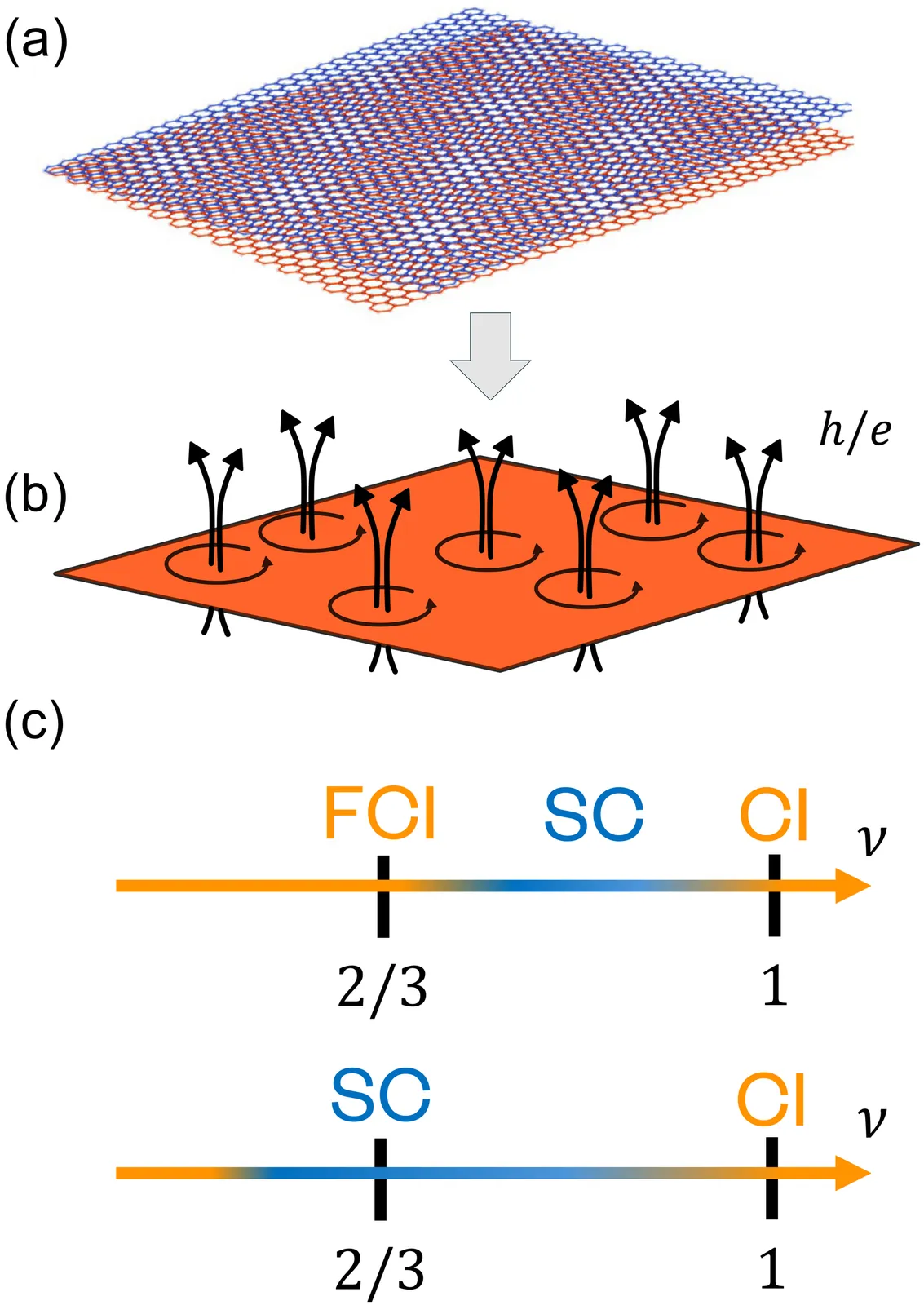
Topological superconductivity with emergent vortex lattice in twisted semiconductors
The coexistence of superconductivity and fractional quantum anomalous Hall (FQAH) effect has recently been observed in twisted MoTe$_2$ and theoretically demonstrated in a model of repulsively interacting electrons under an emergent magnetic field arising from the layer pseudospin texture in moiré superlattice. Here, we show that this superconducting state is a chiral $f$-wave superconductor hosting an array of $double$ vortices, which are induced by the emergent magnetic field with $h/e$ flux quanta per moiré unit cell. This superconducting vortex lattice state is topological and features Chern number $-1/2$, giving rise to a half-integer thermal Hall conductance. Our theory provides a common mechanism and unified understanding of FQAH and topological superconductivity, with a rich phase diagram controlled by the spatial modulation of the emergent magnetic field.
2602.15106
Feb 2026Superconductivity
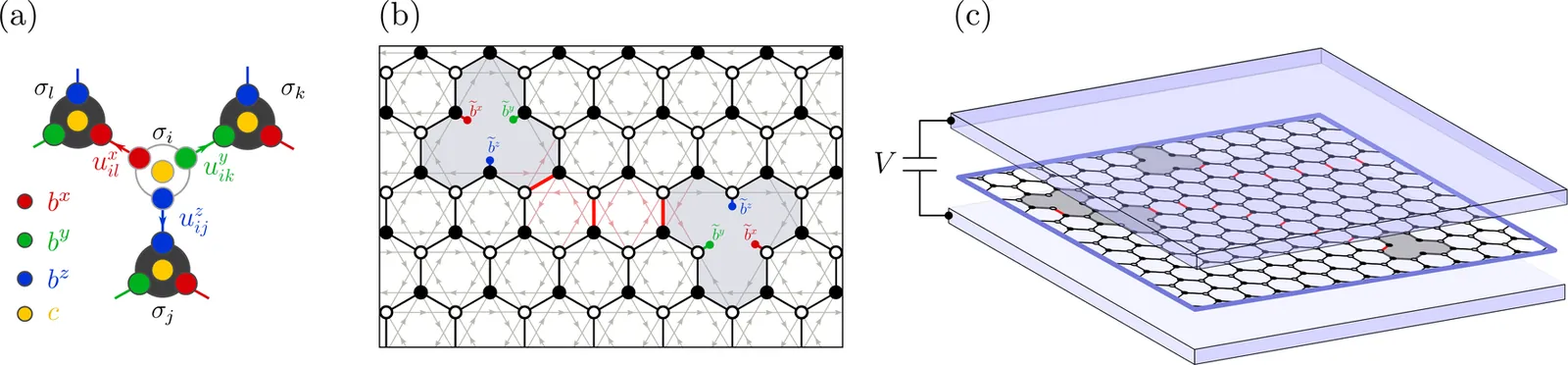
Majorana Signatures in Planar Tunneling through a Kitaev Spin Liquid
We propose a planar tunneling setup to probe vacancy-bound Majorana modes in the chiral Kitaev spin liquid. In this geometry, the inelastic tunneling conductance can be expressed directly in terms of real-space spin correlations, establishing a link between measurable spectra and the underlying fractionalized excitations. We show that spin vacancies host localized Majorana states that generate sharp near-zero-bias features, well separated from the continuum of bulk spin excitations. Compared to local STM measurements, the planar configuration naturally enhances the signal by coherently summing over multiple vacancies, reducing spatial resolution requirements. Our results demonstrate a realistic and scalable route to detect Majorana excitations in Kitaev materials.
2602.15020
Feb 2026Strongly Correlated Electrons
Entanglement negativity in decohered topological states
We investigate universal entanglement signatures of mixed-state phases obtained by decohering pure-state topological order (TO), focusing on topological corrections to logarithmic entanglement negativity and mutual information: topological entanglement negativity (TEN) and topological mutual information (TMI). For Abelian TOs under decoherence, we develop a replica field-theory framework based on a doubled-state construction that relates TEN and TMI to the quantum dimensions of domain-wall defects between decoherence-induced topological boundary conditions, yielding general expressions in the strong-decoherence regime. We further compute TEN and TMI exactly for decohered $G$-graded string-net states, including cases with non-Abelian anyons. We interpret the results within the strong one-form-symmetry framework for mixed-state TOs: TMI probes the total quantum dimension of the emergent premodular anyon theory, whereas TEN detects only its modular part.
2602.16597
Feb 2026Strongly Correlated Electrons
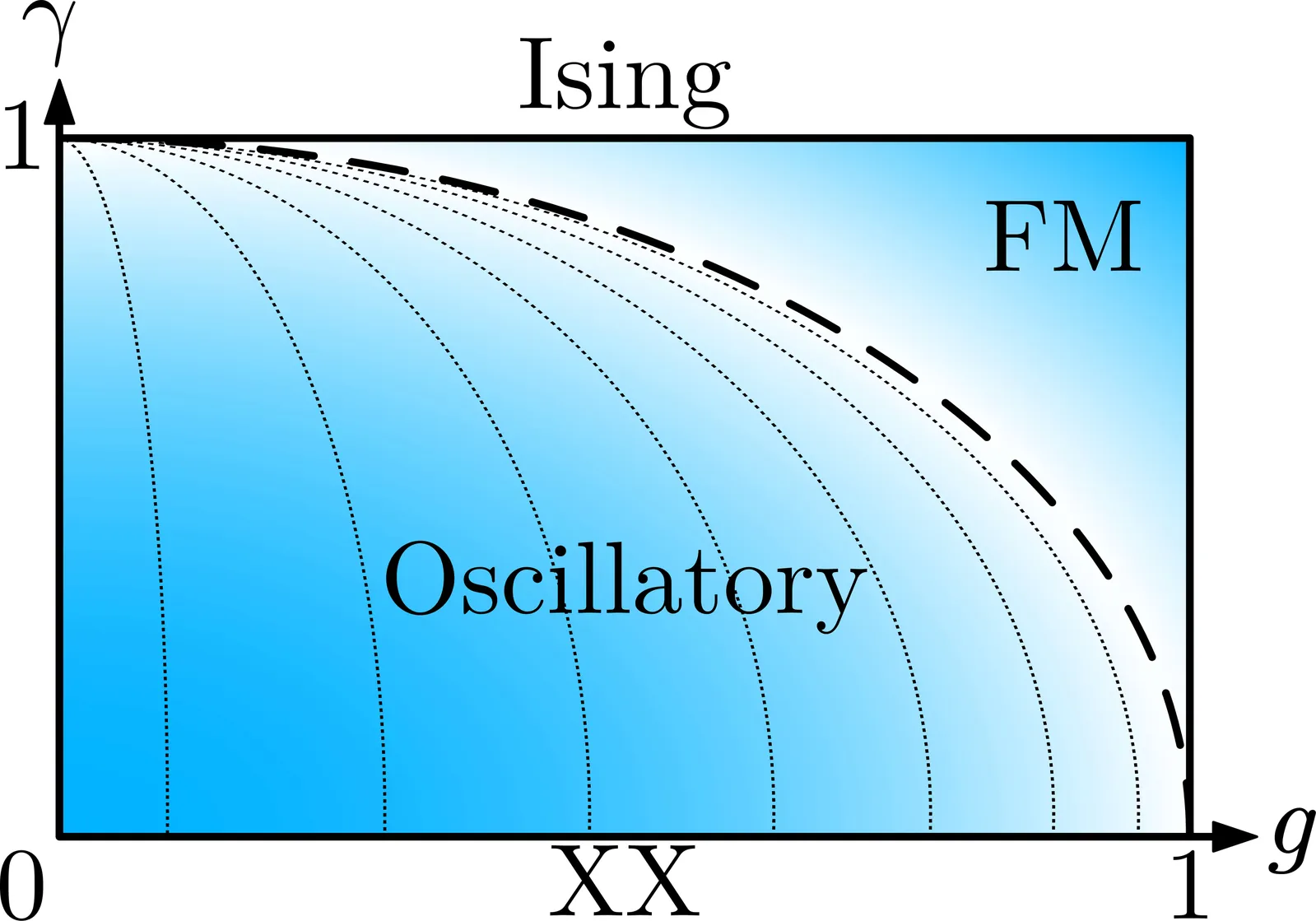
Giant bubbles of Fisher zeros in the quantum XY chain
We demonstrate an alternative approach based on complex-valued inverse temperature and partition function to probe quantum phases of matter with nontrivial spectra and dynamics. It leverages thermofield dynamics (TFD) to quantitatively characterize quantum and thermal fluctuations, and exploit the correspondence between low-energy excitations and Fisher zeros. Using the quantum XY chain in an external field as a testbed, we show that the oscillatory gap behavior manifests as oscillations in the long-time dynamics of the TFD spectral form factor. We also identify giant bubbles, i.e. large-scale closed lines, of Fisher-zeros near the gapless XX limit. They provide a characteristic energy scale that seems to contradict the predictions of the low energy theory of a featureless Luttinger liquid. We identify this energy scale and relate the motion of these giant bubbles with varying external field to the transfer of spectral weight from high to low energies. The deep connection between Fisher zeros, dynamics, and excitations opens up promising avenues for understanding the unconventional gap behaviors in strongly correlated many-body systems.
2602.05899
Feb 2026Strongly Correlated Electrons
Complex nonlinear sigma model
Motivated by the recent interest in the criticality of open quantum many-body systems, we study nonlinear sigma models with complexified couplings as a general framework for nonunitary field theory. Applying the perturbative renormalization-group analysis to the tenfold symmetric spaces, we demonstrate that fixed points with complex scaling dimensions and critical exponents arise generically, without counterparts in conventional nonlinear sigma models with real couplings. We further clarify the global phase diagrams in the complex-coupling plane and identify both continuous and discontinuous phase transitions. Our work elucidates universal aspects of critical phenomena in complexified field theory.
2601.20166
Jan 2026Statistical Mechanics
 2602.16076
2602.16076The most general four-derivative Unitary String Effective Action with Torsion and Stringy-Running-Vacuum-Model Inflation: Old ideas from a modern perspective
The string-inspired running vacuum model (StRVM) of inflation is based on a Chern-Simons (CS) gravity effective action, in which the only four-spacetime-derivative-order term is a gravitational anomalous CS Pontryagin density coupled to an axion. In this work, we revisit curvature-squared string-inspired effective actions, from the point of view of appropriate local field redefinitions, leaving the perturbative string scattering matrices invariant. We require simultaneously unitarity and torsion interpretation of the field strength of the Kalb-Ramond antisymmetric tensor, features characterising the (3+1)-dimensional StRVM Cosmology. Unlike the higher dimensional case, the above feature is possible in the context of (3+1)-dimensional spacetimes, obtained after string compactification. We demonstrate that the unitarity and torsion-interpretation requirements lead to a single-type of extra four-derivative terms in the effective gravitational action, not discussed in the previous literature of StRVM, which however is shown to be subleading by many orders of magnitude, compared to the terms of the StRVM framework. Hence, its presence has no practical implications for the relevant inflationary (and, hence, postinflationary) physics of the StRVM. This demonstrates the phenomenological completeness of the StRVM cosmological scenario, which is thus fully embeddable in the UV complete (quantum-gravity compatible) string theory framework.
2602.16076
Feb 2026General Relativity and Quantum Cosmology
 2601.10428
2601.10428Analyzing intermittent stochastic gravitational wave background I:Effect of detector response
With the growing number of gravitational-wave detections, particularly from binary black hole mergers, there is increasing anticipation that an astrophysical background, formed by an ensemble of faint, high-redshift events, will be observed in the near future by the ground-based detector network. This background is anticipated to exhibit non-Gaussian statistical properties. To develop a robust method for detecting such a non-Gaussian gravitational-wave background, we revisit optimal detection strategies based on the Gaussian-mixture likelihood model. In this work, we demonstrate that properly accounting for the detector antenna pattern is essential. Current approaches typically rely on the overlap reduction function averaged over the sky. Through simulations, we show that using such an averaged response introduces significant biases in parameter estimation. In addition, we propose a computationally feasible method that incorporates second-order corrections as an approximation of the full integral over the source distribution. Our results indicate that this approach effectively eliminates these biases. We also show that our method remains robust even when considering anisotropic backgrounds.
2601.10428
Jan 2026General Relativity and Quantum Cosmology
The emergence of our Universe
We show how our Universe can emerge from a symmetry breaking of a multicomponent $W_3$ algebra, where the components in addition form a Jordan algebra. We discuss how symmetry breaking related to the Jordan algebras $H_3(C)$ and $H_3(O)$ over the complex and octonion numbers can lead to an extended four-dimensional spacetime, where the expansion of the Universe is governed by a modified Friedmann equation. We finally discuss how this modified Friedmann equation might explain a number of puzzling cosmological observations.
2601.10499
Jan 2026General Relativity and Quantum Cosmology
Cosmic Acceleration from Quantum Gravity: Emergent Inflation and Dynamical Dark Energy
We present a mechanism for the emergence of cosmic acceleration within the mean-field approximation of Group Field Theory models of quantum gravity. Depending on the interaction type, the resulting cosmological dynamics can either feature a late-time attractor corresponding to a dynamical dark energy phase, often with characteristic phantom behavior, including in models inspired by simplicial gravity, or instead support an early slow-roll inflationary epoch driven by the same underlying quantum-gravitational effects. This emergent inflation, effectively captured by a single-field description, can sustain the required expansion, naturally avoids the graceful exit problem, and appears to transition into a persistent, non-accelerating phase consistent with classical expectations.
2512.11712
Dec 2025General Relativity and Quantum Cosmology
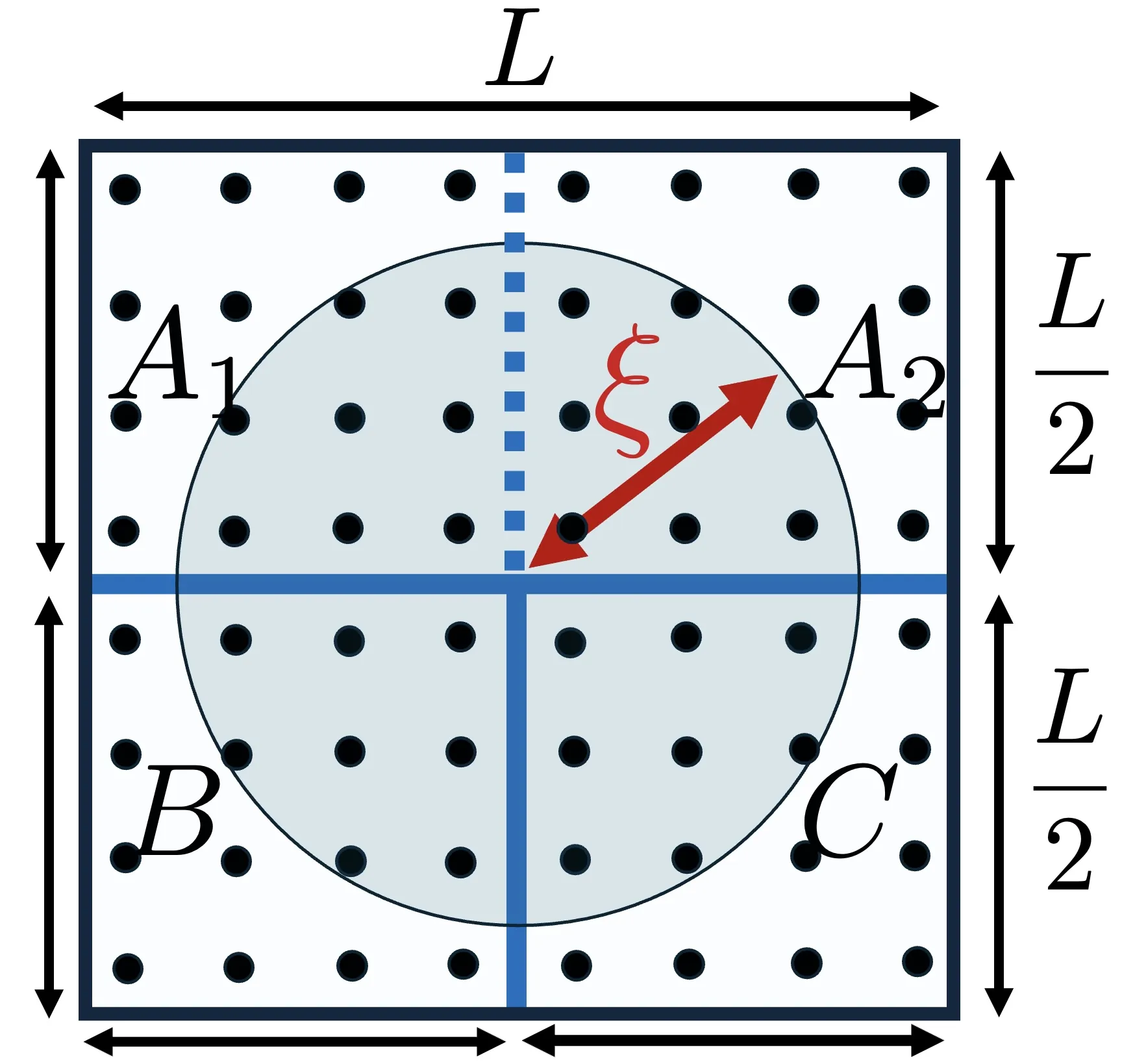
Where Multipartite Entanglement Localizes: The Junction Law for Genuine Multi-Entropy
We uncover a "junction law" for genuine multipartite entanglement, suggesting that in gapped local systems multipartite entanglement is controlled and effectively localized near junctions where subsystem boundaries meet. Using the Rényi-2 genuine multi-entropy $\mathrm{GM}^{(\mathtt{q})}_2$ as a diagnostic of genuine $\mathtt{q}$-partite entanglement, we establish this behavior in $(2+1)$-dimensional gapped free-fermion lattices with correlation length $ξ$. For partitions with a single junction, $\mathrm{GM}^{(\mathtt{q})}_2$ exhibits a universal scaling crossover in $L/ξ$, growing for $L\llξ$ and saturating to a $ξ$-dependent constant for $L\ggξ$, up to $\mathcal{O}(e^{-L/ξ})$ corrections. In sharp contrast, for partitions without a junction, $\mathrm{GM}^{(\mathtt{q})}_2$ is exponentially suppressed in $L/ξ$ and drops below numerical resolution once $L\ggξ$. We observe the same pattern for $\mathtt{q}=3$ (tripartite) and $\mathtt{q}=4$ (quadripartite) cases, and further corroborate this localization by translating the junction at fixed system size. We also provide a geometric explanation of the junction law in holography. Altogether, these results show that in this gapped free-fermion setting genuine multipartite entanglement is localized within a correlation-length neighborhood of junctions.
2602.16331
Feb 2026High Energy Physics - Theory
Toward a mathematically consistent theory of semiclassical gravity or, How to have your wormholes and factorize, too
We review three well known inconsistencies in the standard mathematical formulation of semiclassical gravity: the factorization problem, the information problem, and the closed universe problem. Building upon recent work, we explore how modifying the holographic dictionary may provide the necessary freedom to resolve these three problems in a unified manner while maintaining more well established aspects of the standard correspondence. Using the modified holographic dictionary as a scaffolding, we propose a program for constructing an `extended' semiclassical gravitational path integral which (i) is manifestly factorizing, (ii) computes a von Neumann entropy which satisfies the Page curve, and (iii) incorporates new operators that create closed baby universe states. Our construction may be interpreted as imposing a semiclassical version of background independence/a no global symmetry condition, defining a modified large N limit, preparing an ensemble of dual theories, or enforcing observer rules using gravitational degrees of freedom.
2602.15120
Feb 2026High Energy Physics - Theory
 2602.12176
2602.12176Single-minus gluon tree amplitudes are nonzero
Single-minus tree-level $n$-gluon scattering amplitudes are reconsidered. Often presumed to vanish, they are shown here to be nonvanishing for certain "half-collinear" configurations existing in Klein space or for complexified momenta. We derive a piecewise-constant closed-form expression for the decay of a single minus-helicity gluon into $n-1$ plus-helicity gluons as a function of their momenta. This formula nontrivially satisfies multiple consistency conditions including Weinberg's soft theorem.
2602.12176
Feb 2026High Energy Physics - Theory
 2602.11254
2602.11254Quantum Gravity on AdS$_3\times$S$^3$ from CFT: Bootstrapping $n=21$
We consider the simplest four-point scattering amplitude of $SO(n)$ tensor multiplets in six-dimensional (2,0) supergravity on AdS$_3\times$S$^3$. Using crossing symmetry and the consistency of the operator product expansion in the dual CFT, we explicitly construct the one-loop contribution to the correlator at order $1/c^2$, both in position space and in Mellin space. We show that a strong form of the bootstrap equations imposes constraints on the value of $n$. Remarkably, we find that our bootstrap approach uniquely determines $n=21$, which corresponds to the spectrum of IIB string theory compactified on K3. This stands in sharp contrast to the tree-level correlator for which $n$ is unconstrained. We also analyse the spectrum of unprotected double-trace operators and solve the mixing problem in the first case that involves both tensor and graviton correlators. When $n=21$, the anomalous dimensions rationalise and one of them vanishes. Lastly, we study the flat-space limit of the correlator and find perfect agreement with the one-loop amplitude recently obtained in [arXiv:2510.24558].
2602.11254
Feb 2026High Energy Physics - Theory
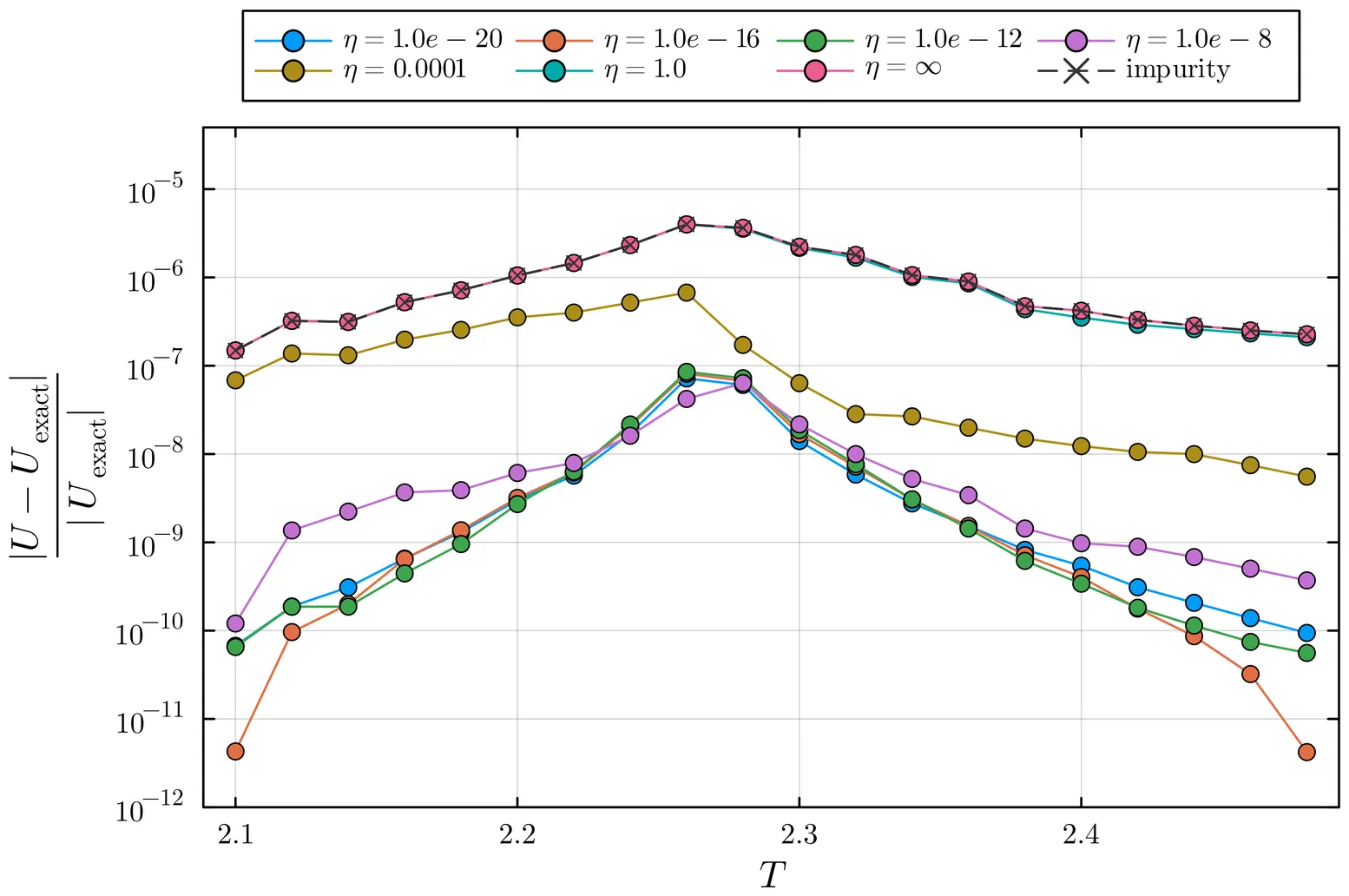
Forward-mode automatic differentiation for the tensor renormalization group and its relation to the impurity method
We propose a forward-mode automatic differentiation (AD) framework for tensor renormalization group (TRG) methods. In this approach, evaluating the derivatives of the partition function up to order $k$ increases the matrix-multiplication cost by a factor of $(k+1)(k+2)/2$ compared to computing the free energy alone, while the memory footprint is only $k$ times that of the original calculation. In the limit where the derivatives of the SVD are neglected, we establish a theoretical correspondence between our forward-mode AD and conventional impurity methods. Numerically, we find that the proposed AD algorithm can calculate internal energy and specific heat significantly higher accuracy than the impurity method at comparable computational cost. We also provide a practical procedure to extract critical exponents from derivatives of the renormalized tensor in TRG calculations in both two and three dimensions.
2602.08987
Feb 2026High Energy Physics - Lattice
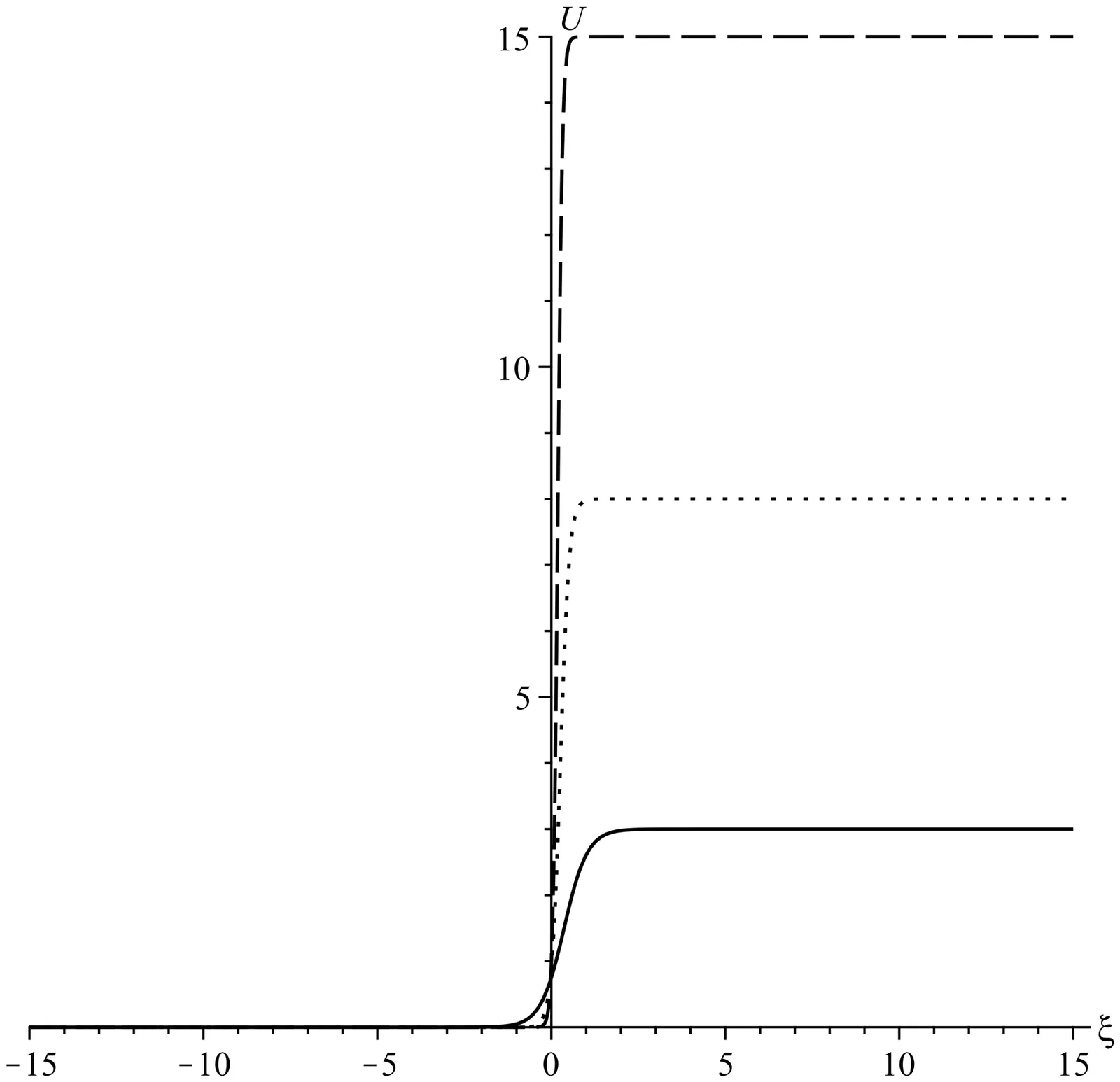
Conservation laws and exact solutions of a nonlinear acoustics equation by classical symmetry reduction
Symmetries and conservation laws are studied for a generalized Westervelt equation which is a nonlinear partial differential equation modelling the propagation of sound waves in a compressible medium. This nonlinear wave equation is widely used in nonlinear acoustics and it is especially important in biomedical applications such as ultra-sound imaging in human tissue. Modern methods are applied to uncover point symmetries and conservation laws that can lead to useful developments concerning solutions and their properties. A complete classification of point symmetries is shown for the arbitrary function. Local low-order conservation laws related to net mass of sound waves are obtained by the multiplier method. Two potential systems are derived yielding potential symmetries and nonlocal conservation laws. For the physical case interesting for this equation, travelling wave solutions are studied leading to shock waves.
2601.085483
Jan 2026Mathematical Physics