General Relativity and Quantum Cosmology

arXiv:gr-qc

General relativity, quantum gravity, cosmological models, gravitational waves, black holes, classical and quantum gravity.

Looking for a broader view? This category is part of:

General Relativity

Trending in General Relativity and Quantum Cosmology

Cosmic Acceleration from Quantum Gravity: Emergent Inflation and Dynamical Dark Energy

We present a mechanism for the emergence of cosmic acceleration within the mean-field approximation of Group Field Theory models of quantum gravity. Depending on the interaction type, the resulting cosmological dynamics can either feature a late-time attractor corresponding to a dynamical dark energy phase, often with characteristic phantom behavior, including in models inspired by simplicial gravity, or instead support an early slow-roll inflationary epoch driven by the same underlying quantum-gravitational effects. This emergent inflation, effectively captured by a single-field description, can sustain the required expansion, naturally avoids the graceful exit problem, and appears to transition into a persistent, non-accelerating phase consistent with classical expectations.

2512.11712

Dec 2025General Relativity and Quantum Cosmology

Related categories:

High Energy Physics - Theory Cosmology and Nongalactic Astrophysics High Energy Astrophysical Phenomena Mathematical Physics Quantum Physics

3,312 papers

A framework for LISA population inference

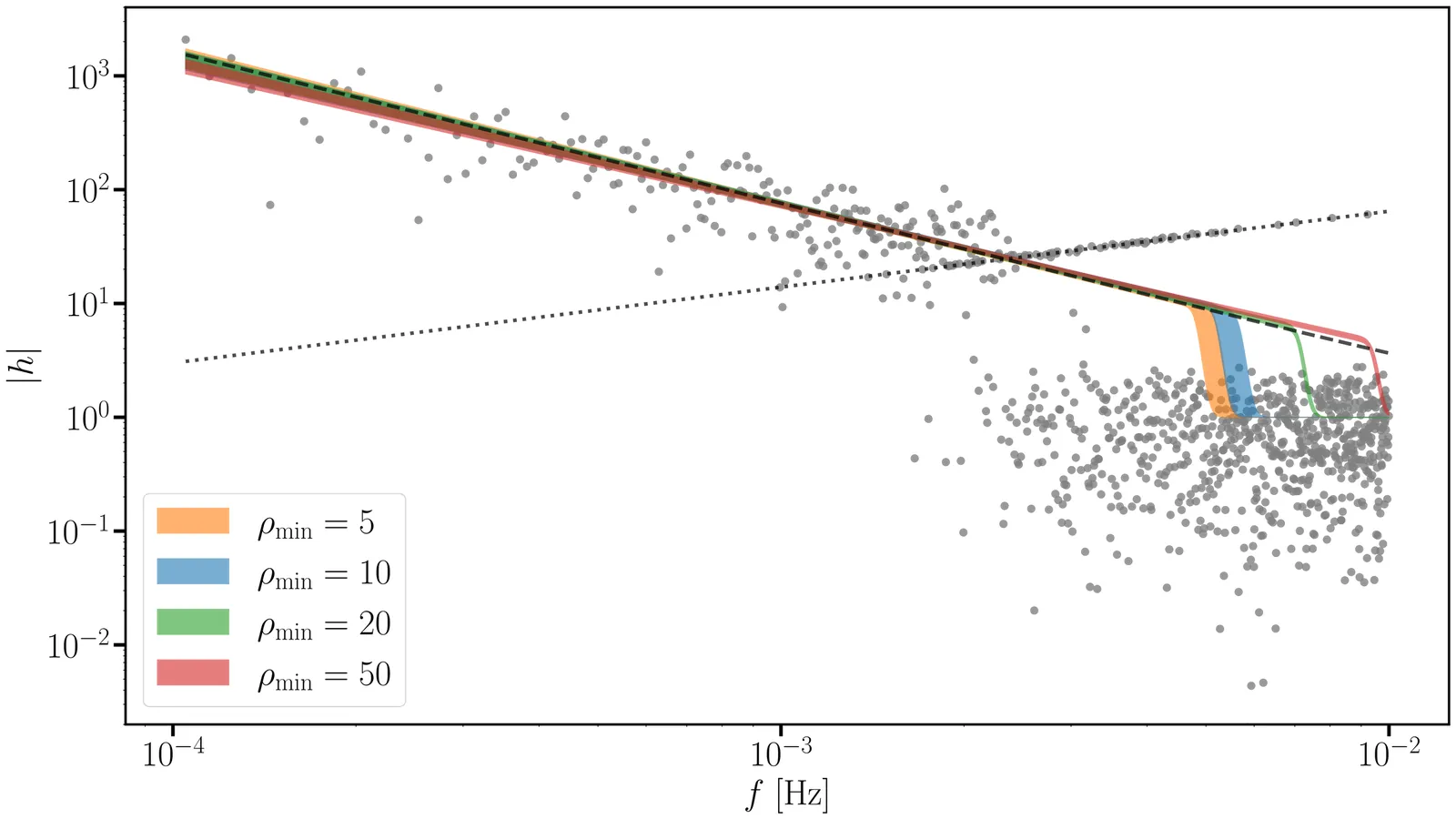
The Laser Interferometer Space Antenna (LISA) is expected to have a source rich data stream containing signals from large numbers of many different types of source. This will include both individually resolvable signals and overlapping stochastic backgrounds, a regime intermediate between current ground-based detectors and pulsar timing arrays. The resolved sources and backgrounds will be fitted together in a high dimensional Global Fit. To extract information about the astrophysical populations to which the sources belong, we need to decode the information in the Global Fit, which requires new methodology that has not been required for the analysis of current gravitational wave detectors. Here, we %start that development, presenting present a hierarchical Bayesian framework to infer the properties of astrophysical populations directly from the output of a LISA Global Fit, consistently accounting for information encoded in both the resolved sources and the unresolved background. Using a simplified model of the Global Fit, we illustrate how the interplay between resolved and unresolved components affects population inference and highlight the impact of data analysis choices, such as the signal-to-noise threshold for resolved sources, on the results. Our approach provides a practical foundation for population inference using LISA data.

2601.04168Jan 2026

View

Obstructions to global visibility of singularities in asymptotically flat spacetimes

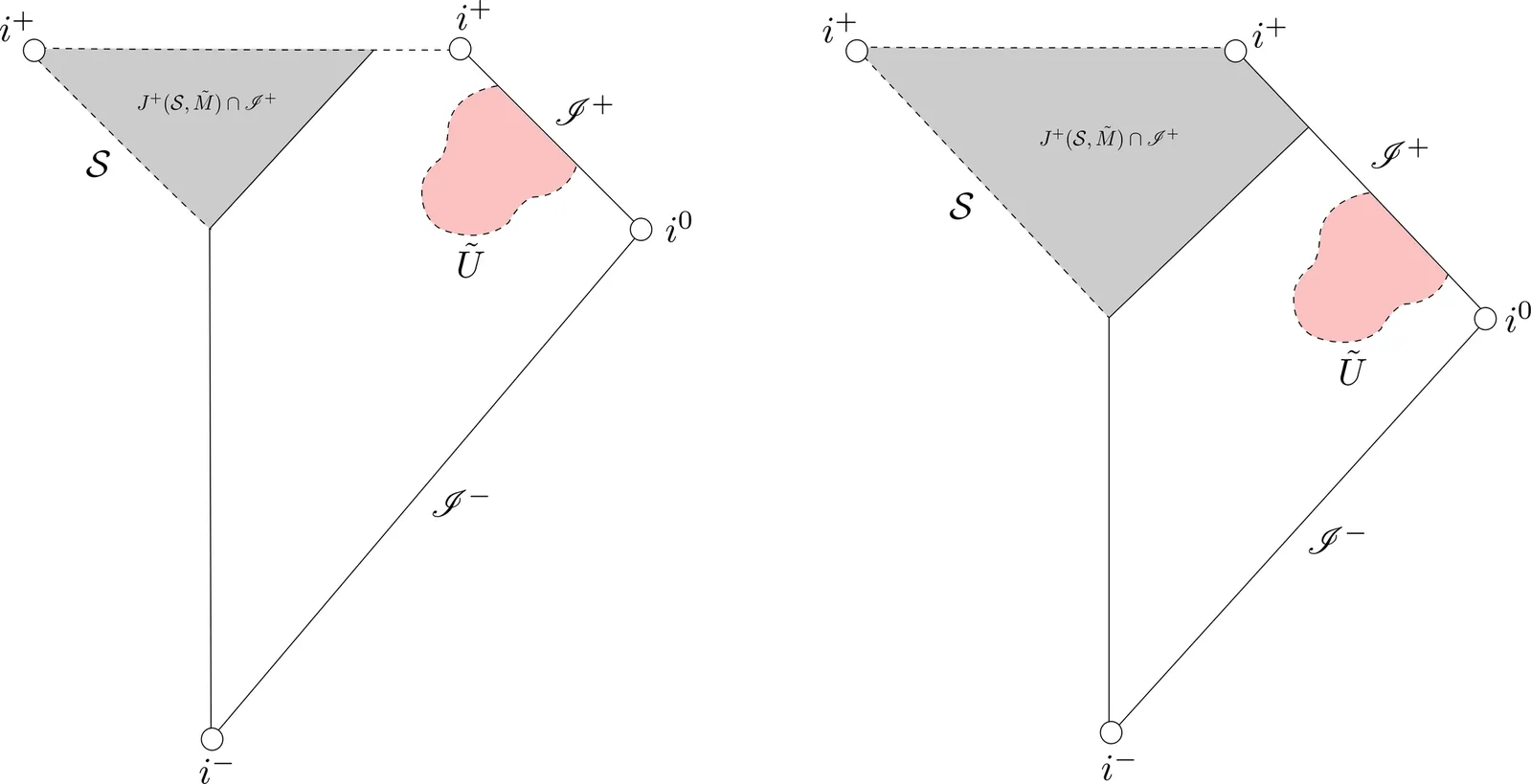
Consider an $(N+1)$-dimensional asymptotically flat spacetime and a future-directed, affinely parametrized outgoing null generator $γ$ of an achronal boundary $\partial J^+(S_\varepsilon)$, where $\{S_\varepsilon\}$ is a nested family of smooth compact codimension $2$ surfaces approaching a singular boundary set $S$ in the past. In the twist-free case and under the null energy condition, the Raychaudhuri equation on the $m:=N-1$ dimensional screen bundle reads, $$ θ'=-\frac1mθ^2-\|σ\|^2-\mathrm{Ric}(k,k), $$ where $k$ is the tangent to $γ$. This equation linearizes, via the rescaling $u:=A^{1/m}$ with $A := |\det D|$ the Jacobi-map $m$-volume, to the Sturm-type ODE $$ u''+\frac1m f\,u=0,\qquad f:=\|σ\|^2+\mathrm{Ric}(k,k)\ge 0. $$ We develop two purely generator-wise criteria forcing a first zero of $u$: (i) an exact Volterra identity combined with concavity leads to a barrier-weighted integral inequality, and (ii) Sturm comparison and a Prüfer-angle estimate yields failure of disconjugacy whenever $\int_c^d \sqrt{f/m}\,dλ>π$ on a subinterval. We prove that $u(λ_\ast)=0$ is equivalent to the existence of a focal (conjugate) point and implies $θ= m u'/u\to-\infty$ at $λ_\ast$. Using the standard structure of achronal boundaries, this yields a geodesic-wise obstruction: if every generator that could reach $\mathscr I^+$ satisfies one of the above conditions in the regular spacetime region, then $J^+(S_\varepsilon)\cap \mathscr I^+=\emptyset$, and hence $S$ is not globally visible. As an application, we illustrate one of these criteria in the Einstein-massless scalar field collapse model of Christodoulou.

2601.04152Jan 2026

View

Parity-violating Dark Photon Halos

We propose a mechanism for the generation of gravitationally bound dark photon halos during the matter-dominated era. Coupled to an ultralight axion field through a parity-violating Chern-Simons term, dark photons can be produced by the tachyonic instability of axion coherent oscillation. The dark photons with a net helicity lead to a metric vorticity and can generate chiral substructures. For axion masses in the range $10^{-28} \, \mathrm{eV} \lesssim m_a \lesssim 10^{-22} \, \mathrm{eV}$, the resulting inhomogeneities collapse to form halos with masses spanning $M_{\rm halo} \sim 10^5 \, M_{\odot}$ to $10^{11} \, M_{\odot}$, with halo sizes ranging from $O(1)$ to $O(10^{6}) \, \mathrm{pc}$. During halo collapse, the induced vorticity could mediate efficient angular-momentum transport, which enables monolithic collapse and provides primordial seeds for the early formation of supermassive black holes.

2601.04145Jan 2026

View

2601.04144

Symmetries of cosmological perturbations: The residual low multipole ambiguity

In cosmology, long-wavelength modes are related to large-gauge transformations (LGT), i.e. changes of coordinates that modify the physical geometry of the cosmological patch. These LGTs stand as bona-fide symmetries of cosmological perturbation theory with various applications, from consistency relations constraining cosmological correlators to non-linear conservation laws in the separate-universe approach. In this work, we revisit LGTs and derive two new results. First, we show that the global symmetries already identified in the literature can be extended to local infinite-dimensional symmetries. The associated generators depend on arbitrary functions of time, and generate low-multipole modes that modify the mean curvature energy and the angular momentum of the patch, demonstrating their physical nature. We propose to interpret these low-multipole soft modes as a new cosmological-frame ambiguity that needs to be fixed prior to evaluating cosmological observables. Second, we demonstrate that the adiabatic cosmological perturbations generated by LGTs deform but preserve all the explicit and hidden Killing symmetries of the background geometry. As such, long-wavelength modes stand as a concrete example of algebraically-special cosmological perturbations of Petrov-type O, and inherit the conformal group as isometries and a set of four deformed Killing-Yano tensors and their associated Killing tensors. This opens the possibility to study their effect on cosmological observables in a fully analytic manner.

2601.04144Jan 2026

View

Observational Signatures of Accretion Disks around a Schwarzschild Black Hole in a Hernquist Dark Matter Halo

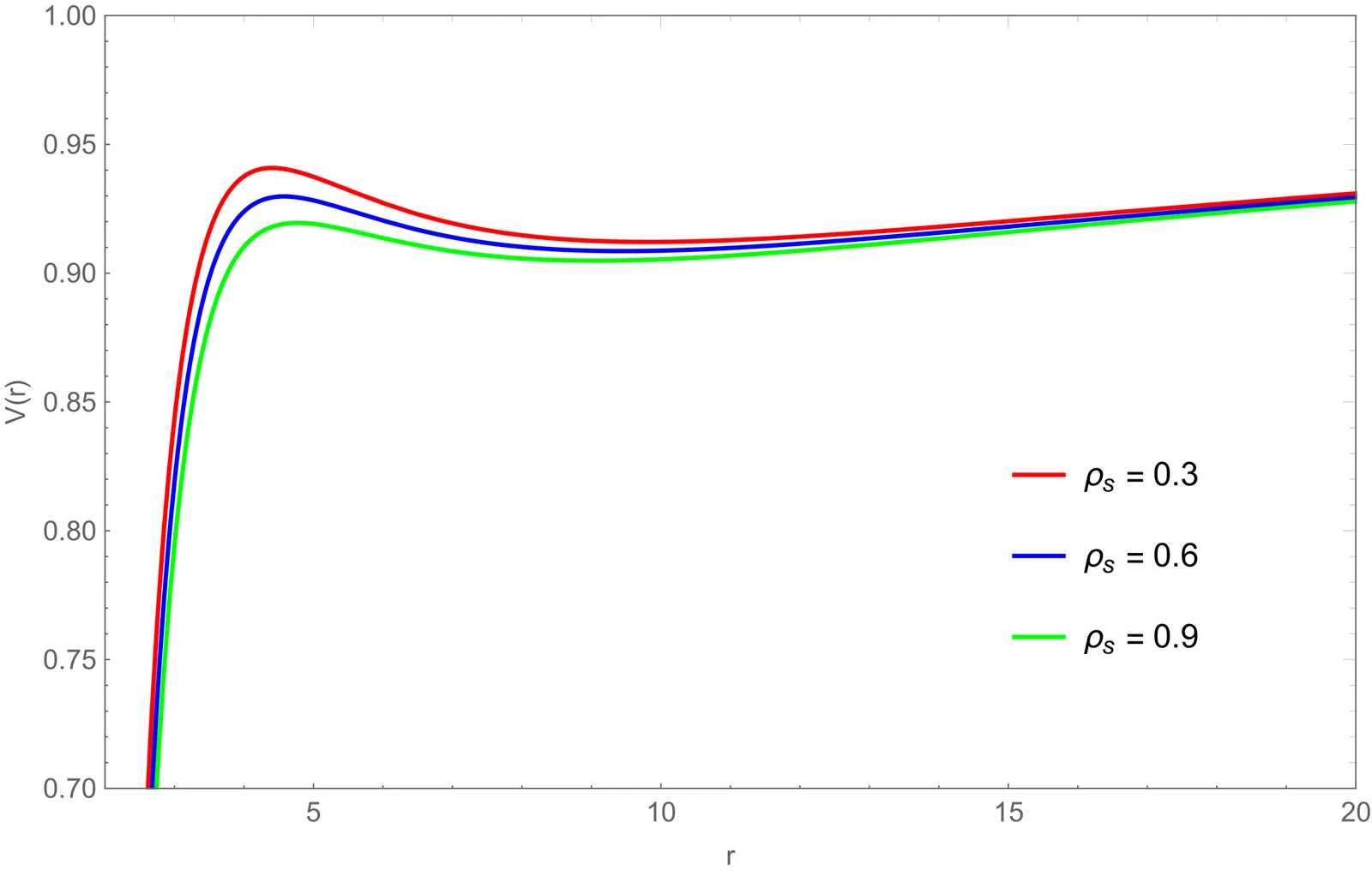
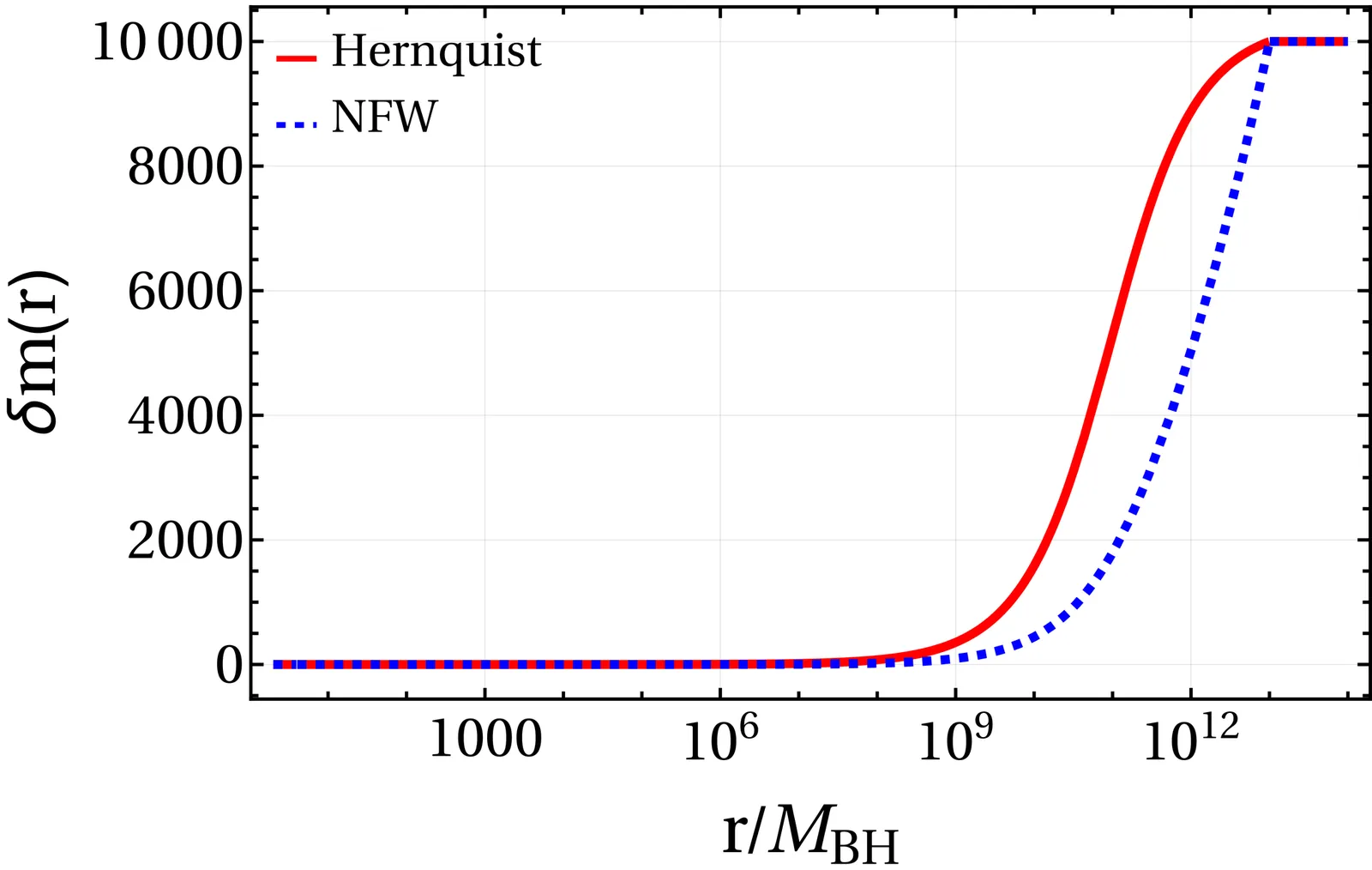
We investigate how a Hernquist type dark matter (DM) halo, parametrized by its core radius $r_{s}$ and central density $ρ_{s}$, influences both the gravitational wave (GW) emission from timelike periodic orbits and the electromagnetic appearance of a thin accretion disk around a Schwarzschild black hole (BH). By analyzing the effective potential for timelike geodesics, we show that the DM halo shifts the marginally bound orbit (MBO) and the innermost stable circular orbit (ISCO) outward, reflecting its modification of the spacetime geometry and the energy-angular momentum structure of particle motion. Employing a semi-analytical method, we compute orbital trajectories and the associated GW waveforms, revealing that the DM halo alters the characteristic zoom-whirl dynamics and induces measurable changes in waveform morphology. Furthermore, we generate direct and secondary images of the accretion disk across various observer inclinations and find that increasing $r_{s}$ or $ρ_{s}$ results in cooler, dimmer disks with modified flux distributions. Our results demonstrate that the presence of a DM halo imprints distinct signatures in both gravitational and electromagnetic observables, offering a multimessenger pathway to probe DM environments near BHs.

2601.03980Jan 2026

View

Combining simulation-based inference and universal relations for precise and accurate neutron star science

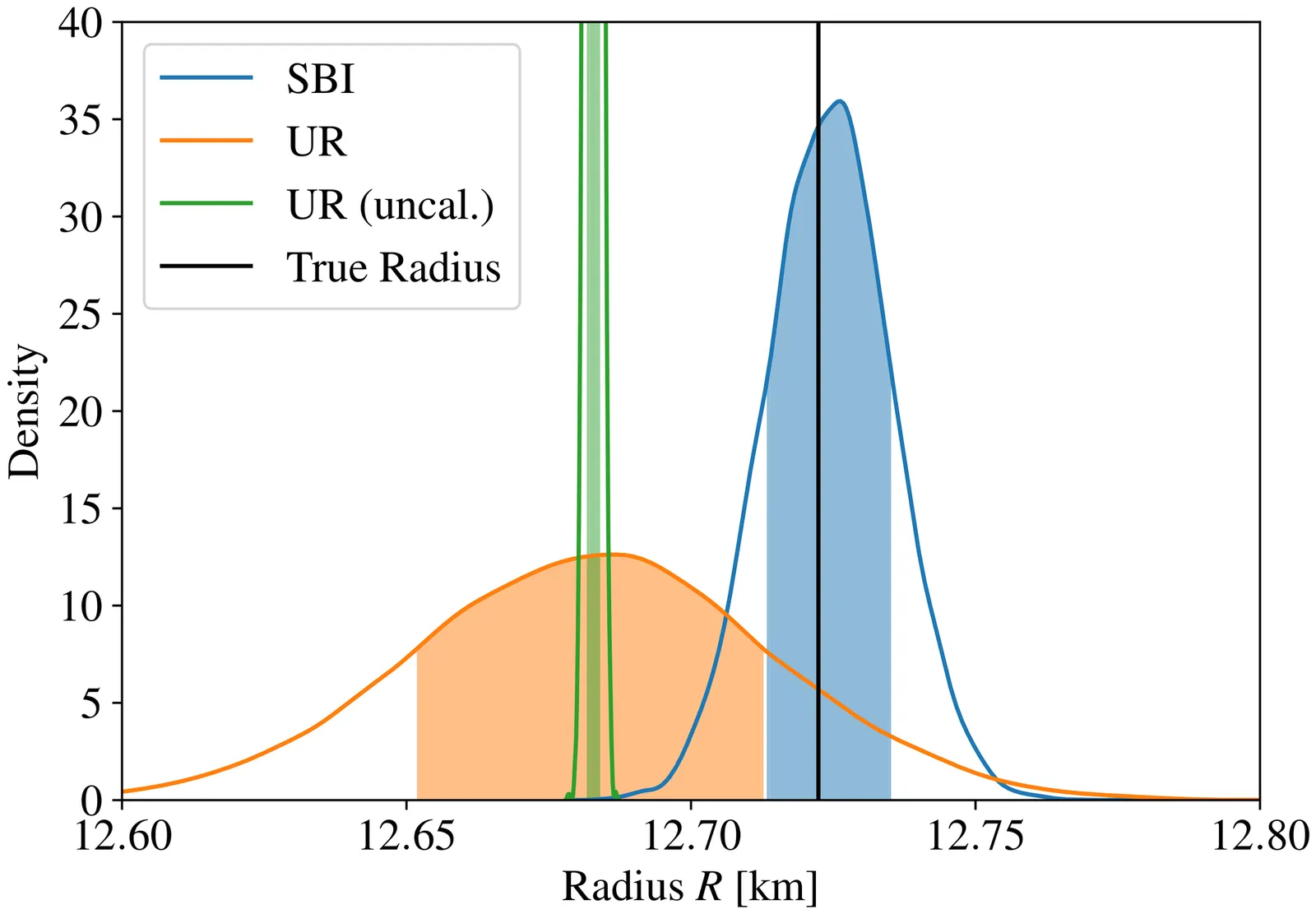
In this work, we propose a novel approach for identifying, constructing, and validating precise and accurate universal relations for neutron star bulk quantities. A central element is simulation-based inference (SBI), which we adopt to treat uncertainties due to the unknown nuclear equation of state (EOS) as intrinsic non-trivial noise. By assembling a large set of bulk properties of non-rotating neutron stars across multiple state-of-the-art EOS models, we are able to systematically explore universal relations in high-dimensional parameter spaces. Our framework further identifies the most promising parameter combinations, enabling a more focused and traditional construction of explicit universal relations. At the same time, SBI does not rely on explicit relations; instead, it directly provides predictive distributions together with a quantitative measure of systematic uncertainties, which are not captured by conventional approaches. As an example, we report a new universal relation that allows us to obtain the radius as a function of mass, fundamental mode, and one pressure mode. Our analysis shows that SBI can surpass the predictive power of this universal relation while also mitigating systematic errors. Finally, we demonstrate how universal relations can be further calibrated to mitigate systematic errors accurately.

2601.03945Jan 2026

View

Motions of spinning particles and chaos bound in Reissner-Nordström spacetime

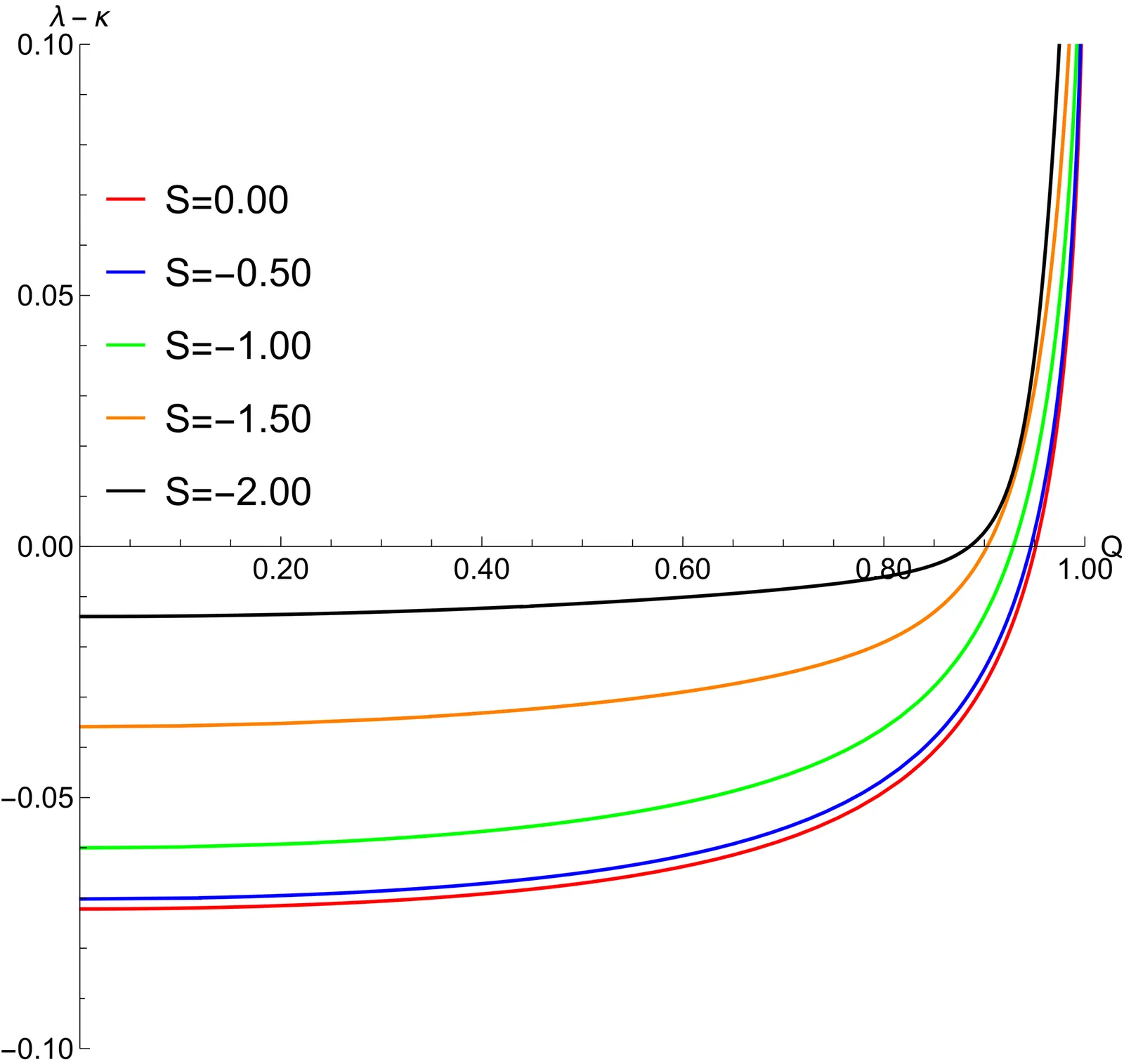
In this paper, we investigate Lyapunov exponents of classical chaos of spinning particles orbiting a Reissner-Nordström black hole and examine whether the values of the exponents exceed the chaos bound. For the neutral particle, when its spin magnitude surpasses a specific threshold, the value of the exponent exceeds the surface gravity, resulting in a violation. Given a fixed total angular momentum of the particle, its spin direction opposite to the angular momentum direction leads to a greater exponent value than when the two directions are aligned. For the charged particle, taking into account the influence of the electromagnetic force, we find that, for relatively large angular momenta, although the electromagnetic force does not change the trend of the exponent's variation with respect to spin and angular momentum and only modifies the specific values of the exponent, it still leads to violations of the bound. Therefore, the chaos bound is violated in the spinor field.

2601.03751Jan 2026

View

Limits on the mass of compact objects in Hořava-Lifshitz gravity

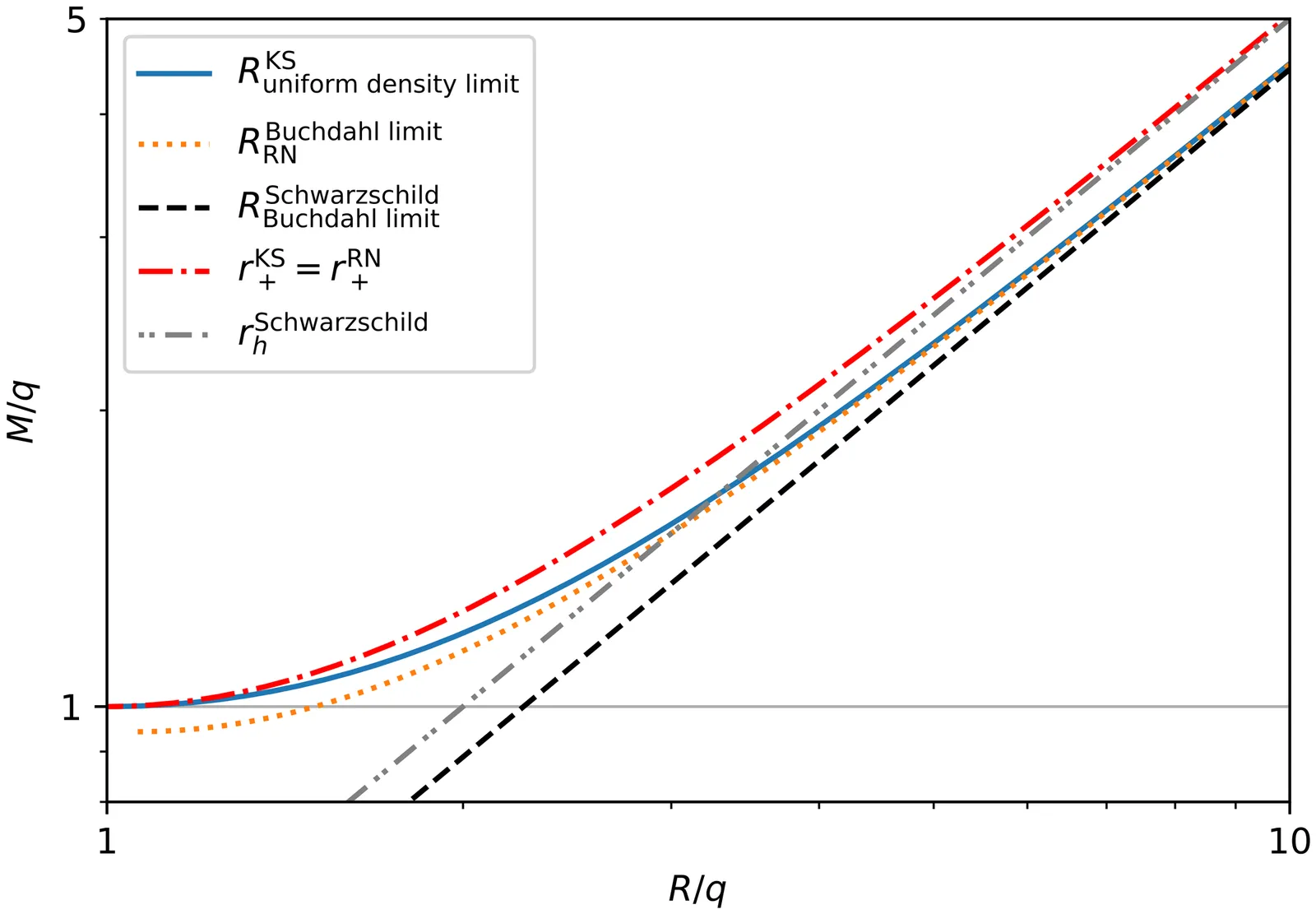
It is known that there exist theoretical limits on the mass of compact objects in general relativity. One is the Buchdahl limit for an object with an arbitrary equation-of-state that turns out to be the limit for an object with uniform density. Another one is the causal limit that is stronger than the Buchdahl limit and is related to the speed of sound inside an object. Similar theoretical limits on the mass of compact objects in deformed Hořava-Lifshitz (HL) gravity are found in this \paper. Interestingly, the both curves of the uniform density limit and the sound speed limit meet the horizon curve at the minimum of the horizon, where a black hole becomes extremal, i.e., $M=q$, considering the Kehagias-Sfetsos vacuum that is an asymptotic flat solution in the HL gravity.

2601.03644Jan 2026

View

Constraining Lorentz and parity violations in gravity with multiband gravitational wave observations

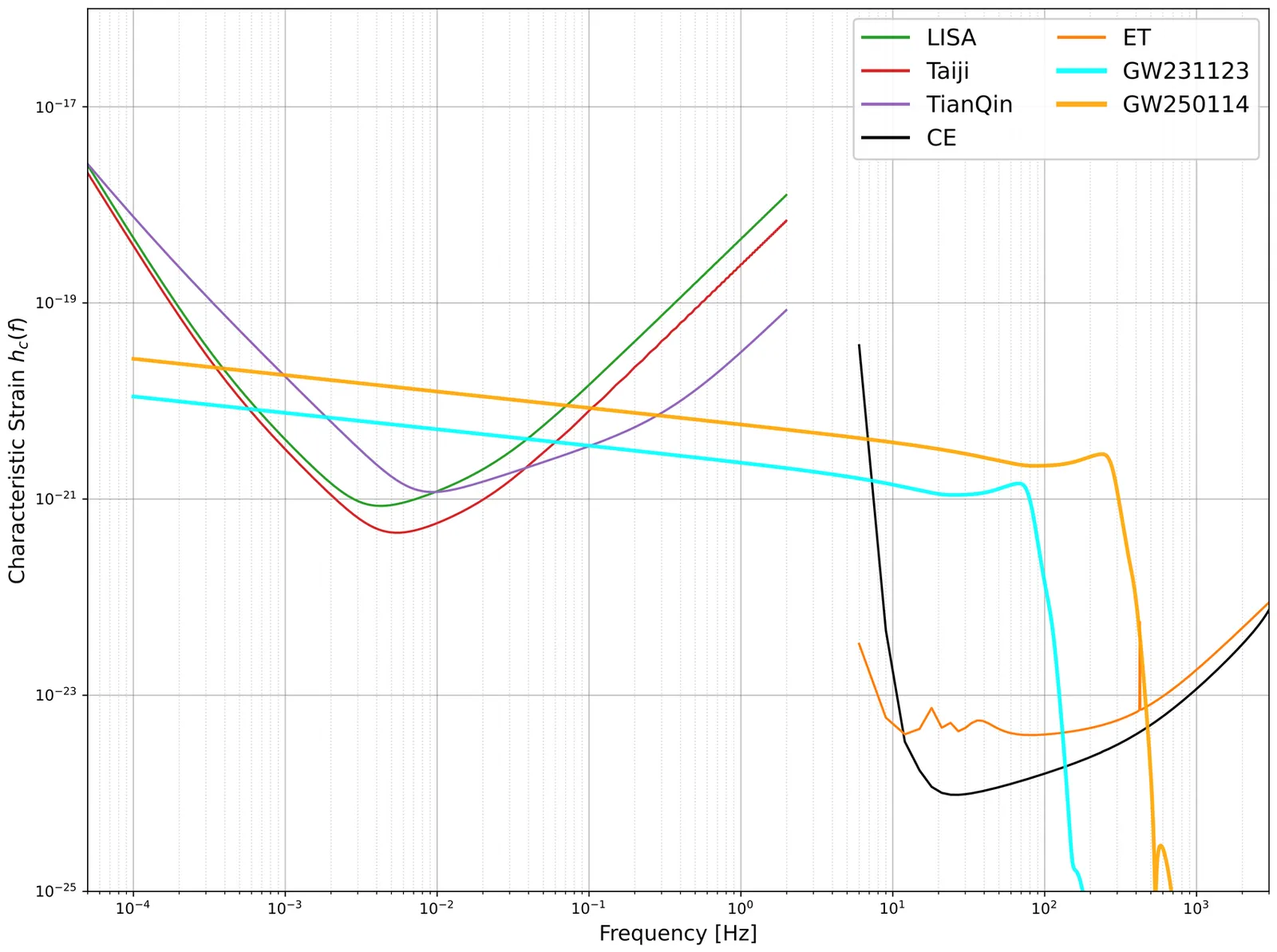
This study evaluates the capability of future multi-band observations of gravitational waves emitted from binary black hole coalescences, utilizing joint third-generation ground-based (CE, ET) and space-based (LISA, Taiji, TianQin) detector networks, to constrain parity and Lorentz symmetry violations in the gravitational sector. We model these effects through a parameterized waveform framework that incorporates a set of parameters that quantify potential deviations from general relativity. The frequency-dependence of their effects is described by power-law indices $β$ (i.e., $β_{\bar ν}$, $β_{\bar μ}$, $β_ν$, and $β_μ$). By analyzing events such as a high-signal noise ratio (SNR) "golden event" like GW250114 and a massive binary system like GW231123 (total mass $190-265 M_\odot$) using two networks of ground- and space-based detectors, we demonstrate that multi-band observations can significantly improve the current constraints on Lorentz and parity violations by several order of magnitude, for both high-frequency ($β> 0$) and low-frequency ($β< 0$) modifications. Our Bayesian analysis reveals that while the exceptional SNR of the GW250114-like event yields superior constraints for high-frequency modifications ($β> 0$), the massive nature of GW231123 provides more stringent limits for low-frequency effects ($β< 0$). This work highlights the critical value of future multi-band gravitational wave astronomy for conducting precision tests of general relativity across diverse binary populations.

2601.03571Jan 2026

View

Superradiant scattering by rotating black-bounce black holes

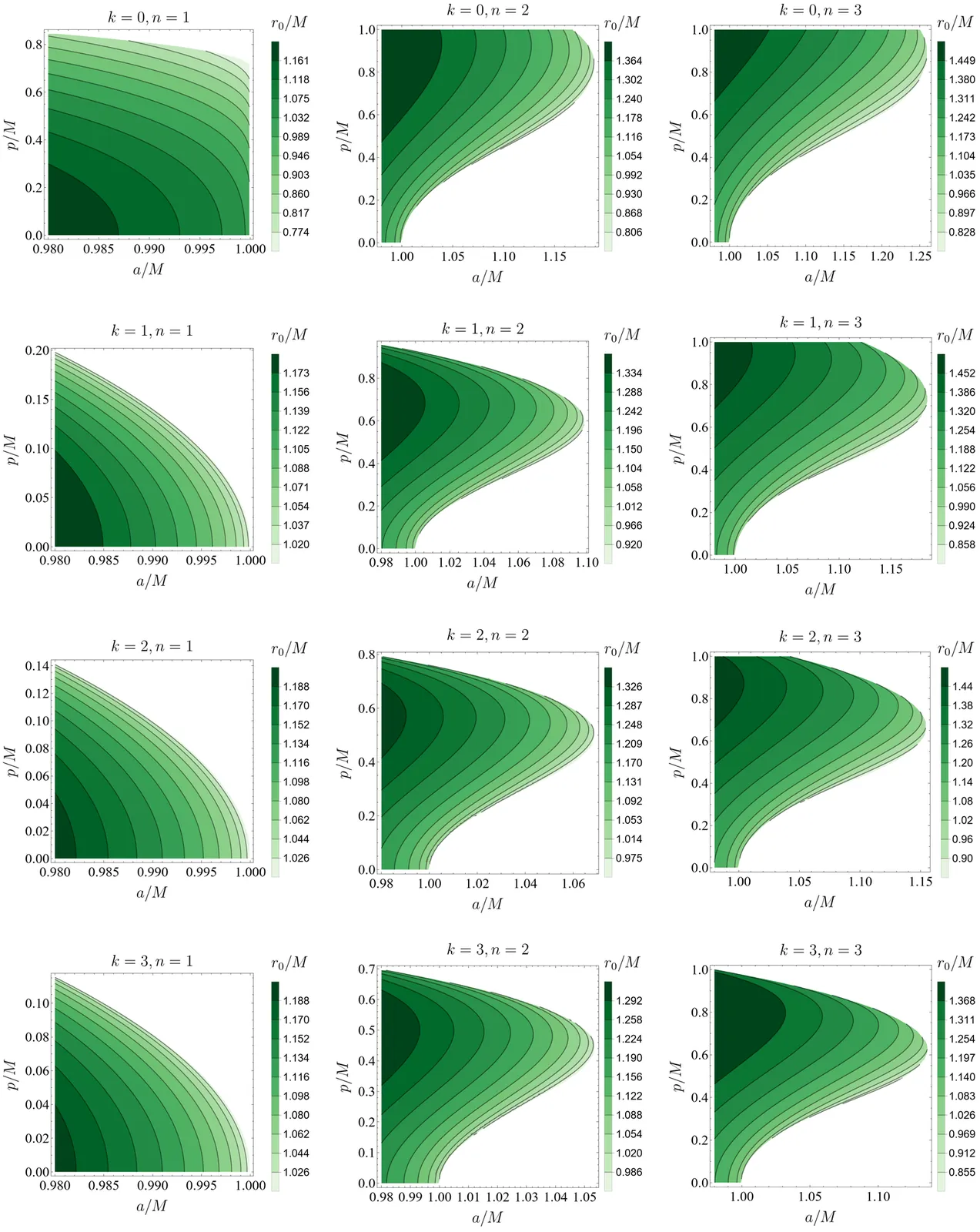
We investigate superradiant scattering off a rotating regular black hole described by a black-bounce metric which generalizes the Kerr spacetime of mass $M$ and specific angular momentum $a$ through a regularization parameter $p$ and two deformation exponents $(k,n)$. Focusing on massless $(\ell,m)=(1,1)$ scalar modes, we explore the parameter space and compute amplification factors by numerically integrating the separated radial Klein-Gordon equation. We track the peak amplification and the corresponding frequency across the $(a/M,p/M)$ parameter space for several combinations of $k$ and $n$. We find that increasing $n$ systematically enhances superradiance, whereas increasing $k$ tends to suppress it. In particular, certain configurations yield amplification levels up to 98% larger than the maximum amplification for standard Kerr black holes.

2601.03415Jan 2026

View

Probing beyond-vacuum general relativistic effects with extreme mass-ratio inspirals

We examine extreme mass-ratio inspirals (EMRIs) as probes of beyond-vacuum general relativistic effects, accounting for both astrophysical environments and scalar Gauss-Bonnet (sGB) gravity. In beyond-vacuum scenarios, the evolution of an EMRI immersed in a cold dark matter environment modifies the gravitational wave flux and introduces additional dissipative effects such as dynamical friction. In parallel, in the beyond-general relativistic settings such as in sGB gravity, the inspiraling object carries an effective scalar charge and emits scalar radiation. Both environmental and modified-gravity effects modify the flux-balance law, thereby inducing changes in the EMRI dynamics. Using a two-timescale analysis within the fixed-frequency formalism, we compute leading-order corrections to the energy fluxes for quasi-circular, equatorial orbits in static, spherically symmetric spacetimes and construct the corresponding gravitational waveforms, which are used to quantify the accumulated gravitational wave dephasing and waveform mismatch relative to the vacuum general relativistic case. We further perform the Fisher Information Matrix analysis to estimate parameter correlations and the ability of future space-based detectors such as the Laser Interferometer Space Antenna (LISA) to disentangle environmental and modified gravity effects. Our results show that both dark matter and scalar field effects can leave measurable imprints on EMRI waveforms and that a consistent beyond-vacuum treatment is essential for robust tests of gravity.

2601.03374Jan 2026

View

Fast frequency-domain phenomenological modeling of eccentric aligned-spin binary black holes

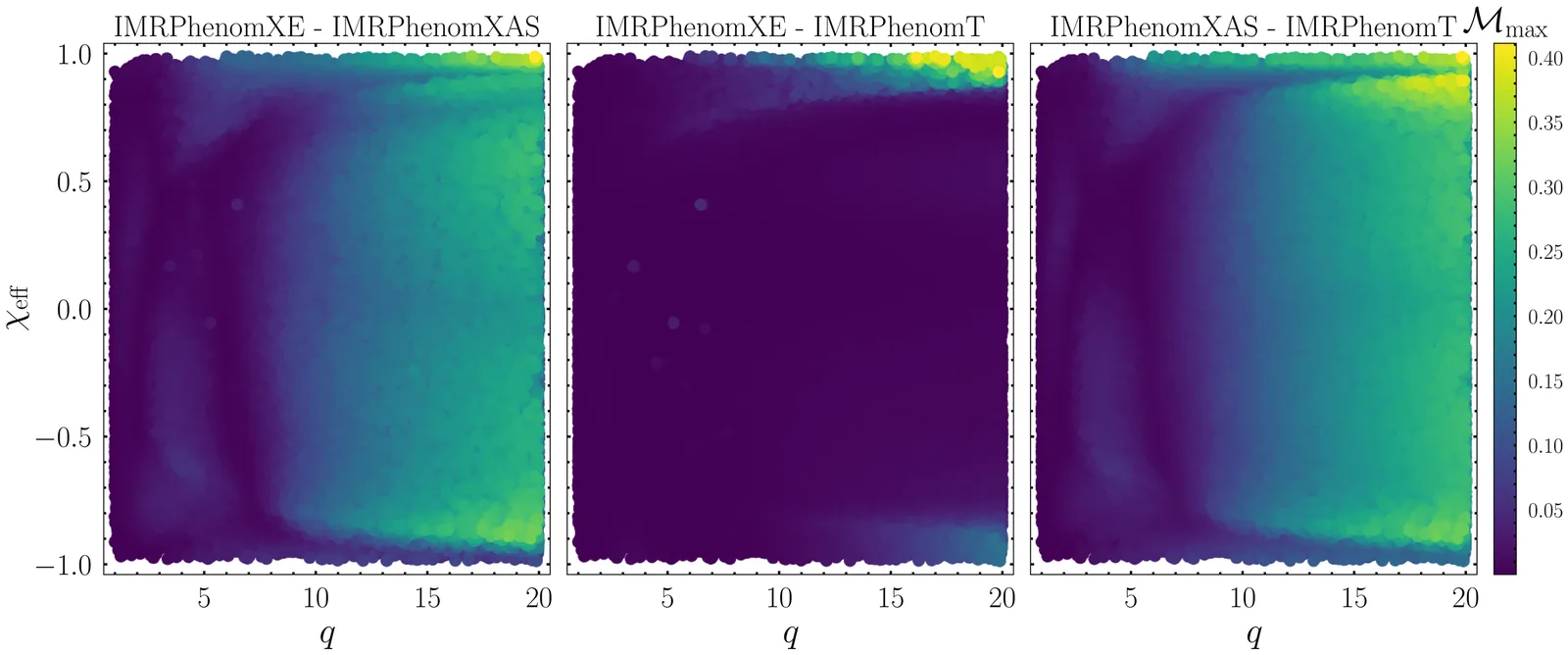
We present the IMRPhenomXE frequency-domain phenomenological waveform model for the dominant mode of inspiral-merger-ringdown non-precessing binary black holes in elliptical orbits. IMRPhenomXE extends the quasi-circular IMRPhenomXAS waveform model for the dominant $(\ell, |m|) =$ (2,2) modes to eccentric binaries. For the inspiral part, orbit-averaged equations of motion within the quasi-Keplerian parametrization up to third post-Newtonian order, including spin effects, are evolved, and the waveform modes are computed using the stationary phase approximation on eccentricity expanded expressions up to $\mathcal{O}(e^{12})$. The model assumes circularization at merger-ringdown, where it adopts the underlying quasicircular IMRPhenomXAS baseline. We show that IMRPhenomXE reduces to the accurate IMPhenomXAS model in the quasi-circular limit. Compared against 186 public numerical relativity waveforms from the Simulating eXtreme Spacetimes catalog with initial eccentricities up to $~0.8$, IMRPhenomXE provides values of unfaithfulness below $3\%$ for $72\%$ of simulations with initial eccentricities below 0.4. For larger eccentricities, the unfaithfulness degrades up to $\gtrsim 10\%$ due to the underlying small eccentricity expansions and additional modelling approximations. In terms of speed, IMRPhenomXE outperforms any of the existing inspiral-merger-ringdown eccentric waveform models. We demonstrate the efficiency, robustness, and modularity of IMRPhenomXE through injections into zero noise and parameter-estimation analyses of gravitational-wave events, showing that IMRPhenomXE is a ready-to-use waveform model for gravitational-wave astronomy in the era of rapidly growing event catalogs.

2601.03340Jan 2026

View

Discrete gravitational diagram technique in the soft synchronous gauge

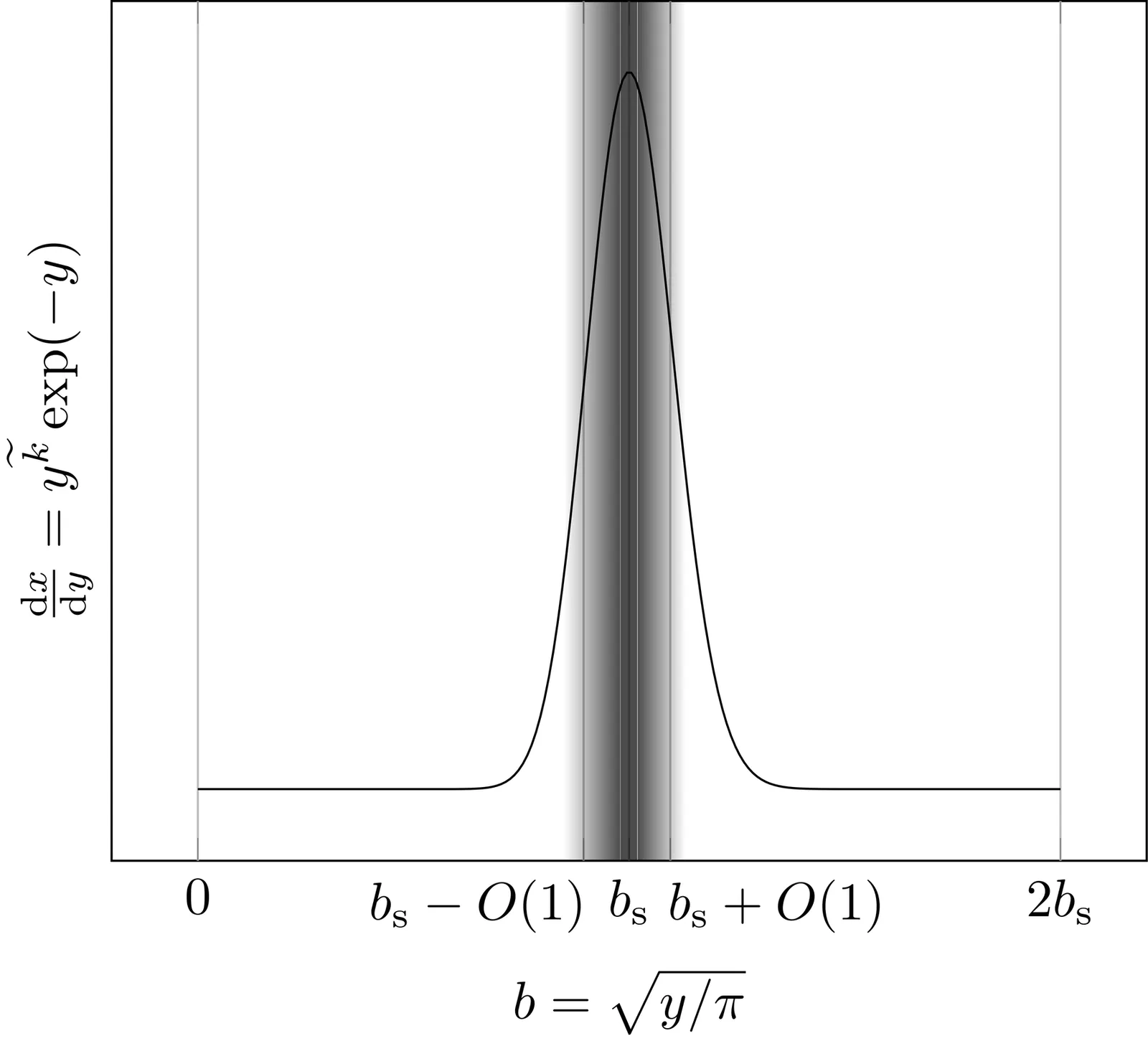
This paper develops our work on the consequences of the Regge calculus, where some edge length scale arises as an optimal starting point of the perturbative expansion with taking into account a bell-shaped form of the measure obtained using functional integration over connection. A "hypercubic" structure is considered (some variables are frozen), it is described by the metric $g_{λμ}$ at the sites. The edge length scale as some maximum point of the measure is $\sim η^{1 / 2}$, where $η$ defines the free factor like $ ( - \det \| g_{λμ} \| )^{ η/ 2}$ in the measure and should be a large parameter to ensure true action upon integration over connection. A priori, the perturbative expansion may contain increasing powers of $η$, but this does not happen for the starting point inside some neighborhood of the maximum point of the measure, and it does happen outside this neighborhood. This appears to be a dynamic mechanism for establishing the edge length scale. We use a discrete version of the soft synchronous gauge in the principal value type prescription we discuss in a recent paper arXiv:2601.02181. This allows one to fix the timelike length scale at a low level for which the measure is known in closed form. This gauge is considered together with a refined finite-difference form of the action to match the analytical properties of the propagator to the continuum case.

2601.03228Jan 2026

View

When does entanglement through gravity imply gravitons?

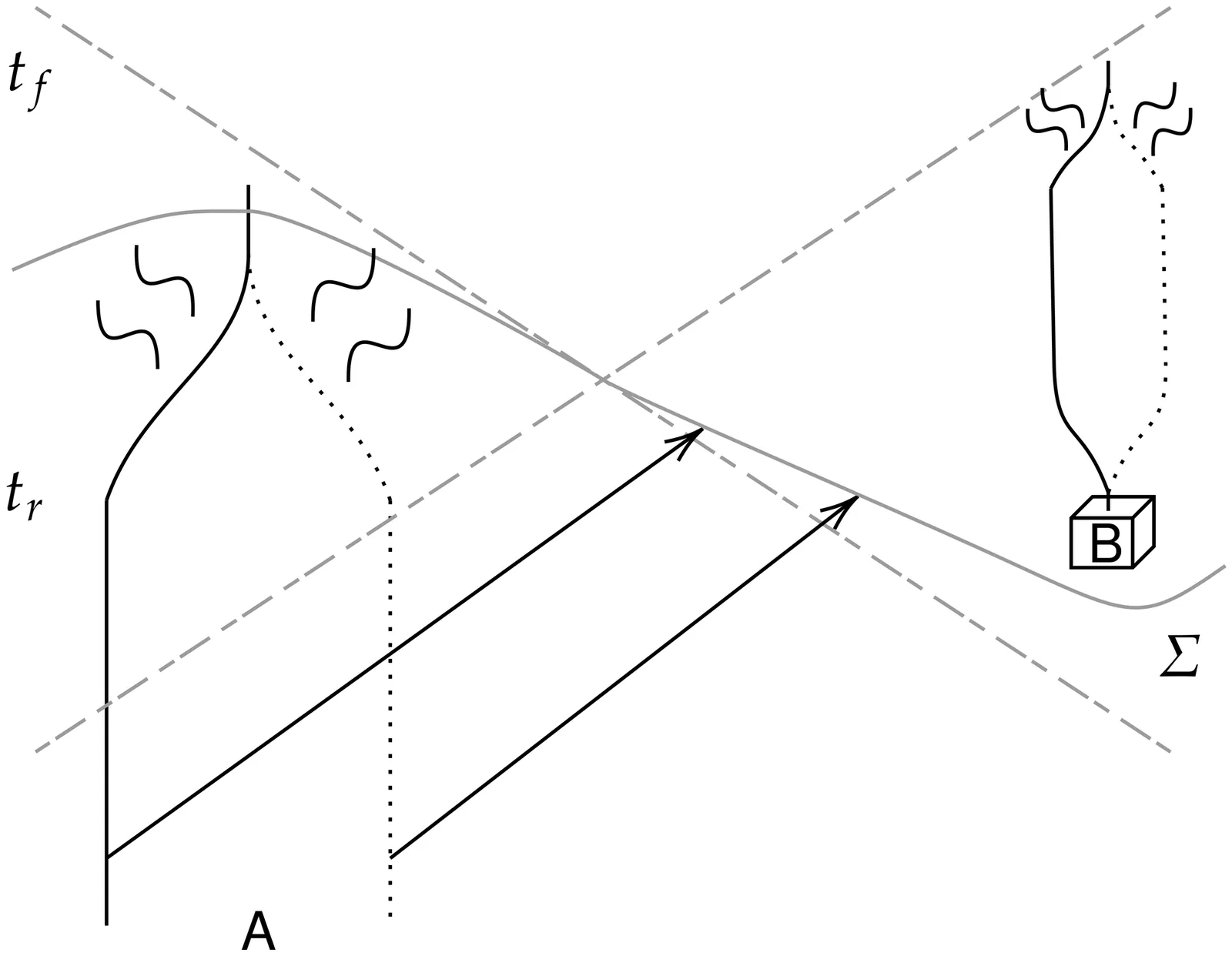
Detection of entanglement through the Newtonian potential has been claimed to support the existence of gravitons, by extrapolating to a thought experiment which demonstrates that complementarity and causality would be in conflict unless quantum fluctuations exist. We critically assess this consistency argument using scalar field models. We show that whether complementarity or no-signalling is violated when quantum fluctuations are neglected, depends on how this approximation is taken, while in both cases entanglement is generated locally in spacetime. We clarify that the correct reading of the paradox requires making a clear distinction between two notions of causality violation: Newtonian action-at-a-distance and the quantum mechanical no-signalling; the latter is pertinent while the former is not. We conclude that the thought experiment (a) does not add to the epistemological relevance of entanglement through Newtonian potentials (b) lends support for the existence of gravitons, if retardation effects are detected in entanglement through gravity.

2601.03214Jan 2026

View

Wave optical imaging by point-source scattering for a TNdS black hole

In our work, we present a calculation based on an exact, non-approximated wave equation, as described by the Teukolsky equation, for a Taub-NUT-de Sitter spacetime. We observe the scattering of a monochromatic point source by an observer located at a greater distance from the black hole, and examine the wave-optical images by a single source and by multiple sources.

2601.03118Jan 2026

View

A Bayesian Statistical Study of Bianchi Type-I Universe in $f(R,T^ψ)$ Modified Gravity

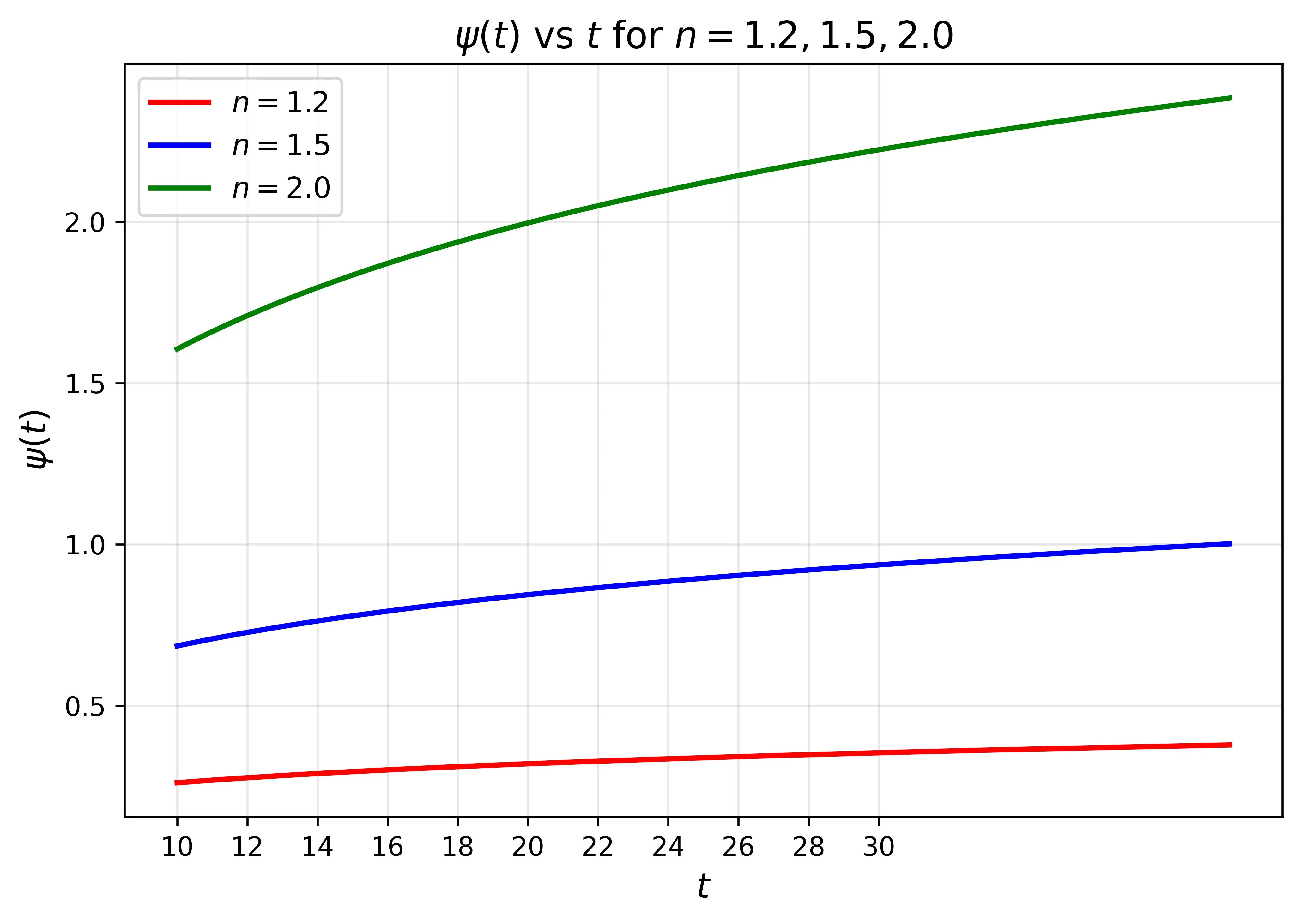
We have examined the cosmological actions of LRS (Locally Rationally Symmetric) Bianchi type-I universe model in $f(R,T^ψ)$ gravity. For this, we have estimated the Hubble parameter, the effective equation of state parameter ($ω^{eff}$), and the potential of the scalar field as a function of time using equation $H = W(ψ)$. The graphical representation of the potential function $V(ψ)$ with respect to cosmic time t is described. This study explores the dynamical properties of a Bianchi Type-I universe by utilizing Bayesian statistical techniques to constrain the model parameters and evaluate the viability of anisotropic cosmology under extended matter-geometry couplings. Also, we have applied the Markov Chain Monte Carlo (MCMC) mechanism on the derived $H(z)$ model by using observational Hubble data (OHD), the Baryon Acoustic Oscillation (BAO) dataset, and the Pantheon dataset. From the confidence-level contours and best-fit parameter values obtained, along with the corresponding reduced $χ^{2}$, it is evident that the model aligns strongly with observational data, demonstrating statistical stability and consistency in describing late-time cosmic acceleration. Likewise, the error analyses presented in this research, including a comparison between the $Λ$CDM cosmology and the reconstructed $H(z)$ model, confirm the model's compatibility with current observations by yielding a reliable and accurate account of the universe's expansion history.

2601.03116Jan 2026

View

Epicyclic motion and accretion disk around a charged black hole in Einstein-ModMax theory with a quintessence field

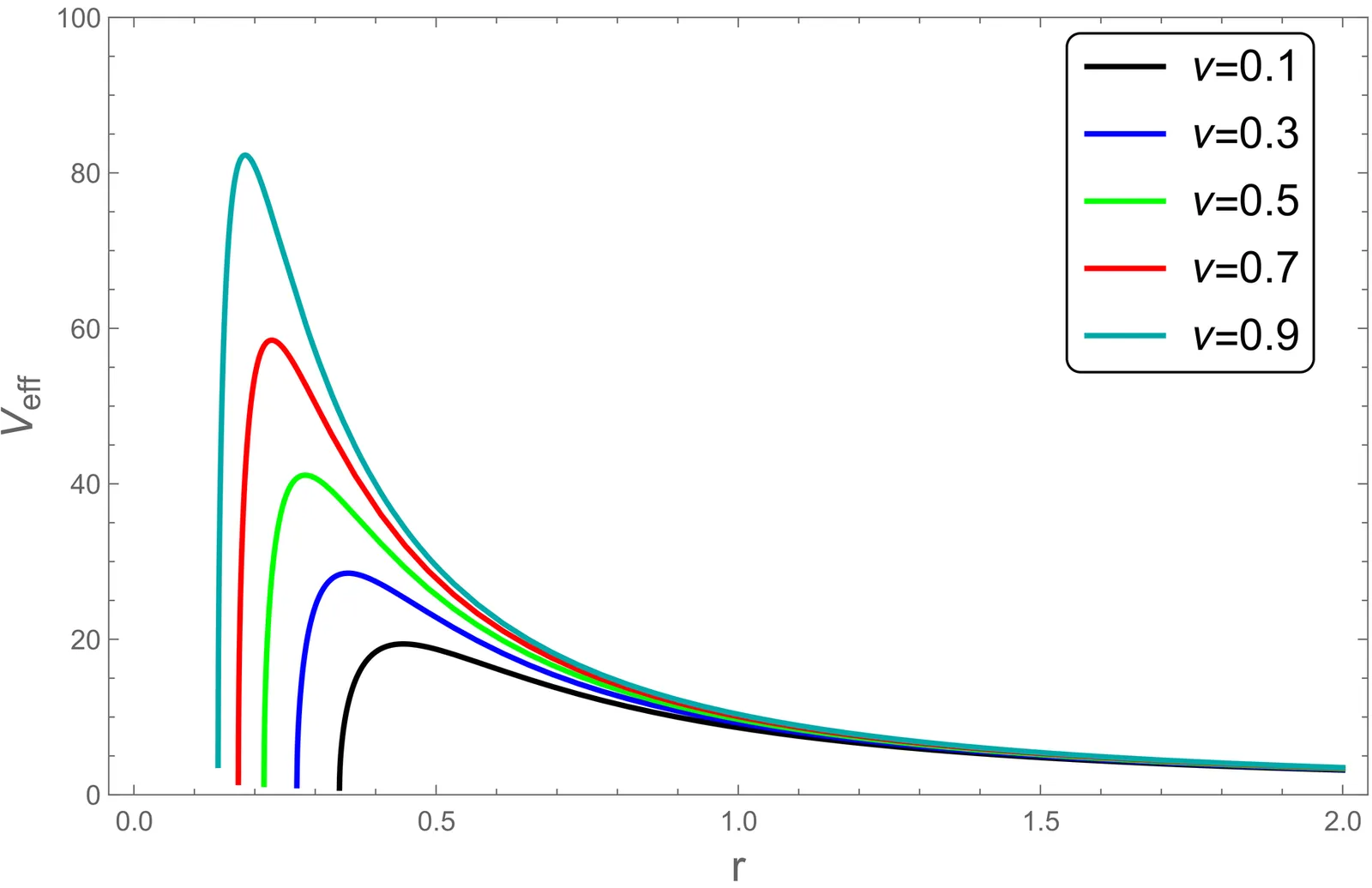
We investigate the epicyclic motion of charged test particles and the associated quasi-periodic oscillations (QPOs) around a weakly magnetized black hole surrounded by quintessence within the framework of Einstein-ModMax theory. We analyze the dynamics of charged particles on circular orbits and derive the corresponding radial and vertical epicyclic frequencies. The influence of the nonlinear electrodynamics parameter, magnetic coupling, dyonic charge, and quintessence state parameter on the innermost stable circular orbit and epicyclic frequencies is examined in detail. Using the forced resonance model, we compare the theoretical predictions of high-frequency QPOs with observational data from several X-ray binary systems. A Markov Chain Monte Carlo analysis is employed to constrain the black hole parameters and assess the role of weak magnetization and nonlinear electrodynamics effects. This analysis indicates that QPO observations tightly constrain the black hole mass and orbital radius while placing stringent upper bounds on the ModMax coupling, magnetic interaction, and dyonic charge. In addition, we study the radiative properties of the accretion disk and analyze the effects of the model parameters on the disk flux and temperature profiles. These findings suggest that the observed QPOs are consistent with general relativity in the strong-field regime, allowing only small deviations associated with Einstein-Maxwell theory in the presence of a quintessence field.

2601.03088Jan 2026

View

Disturbing moving fluids

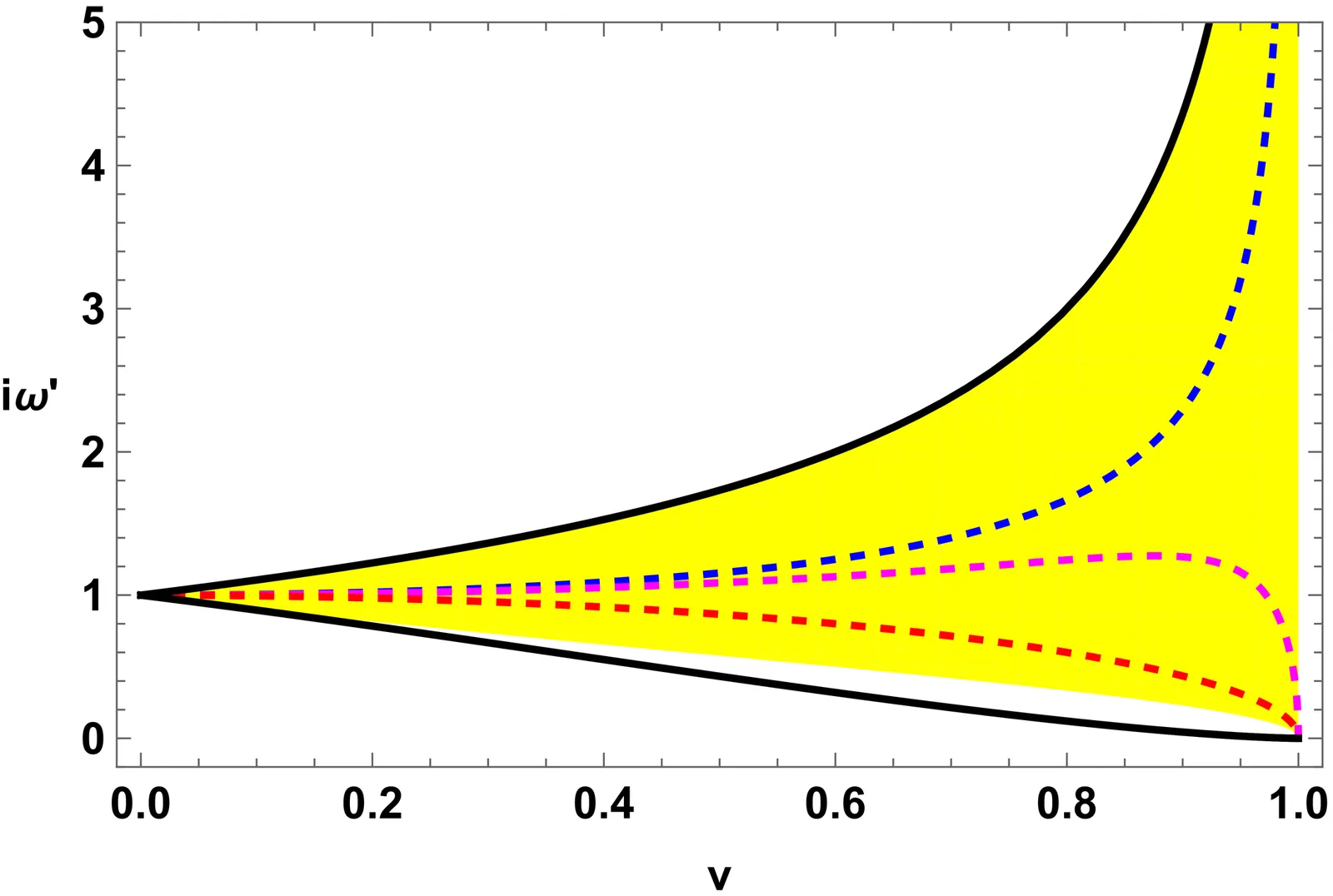
In Newtonian physics, the excitation spectrum of a fluid is the same in all reference frames, up to a trivial shift. In special relativity, this is no longer the case. Relativity of simultaneity causes different inertial observers to measure markedly different excitation spectra, with stability being the only property known to be Lorentz invariant in all causal theories. Here, we show that, under a certain Onsager-like symmetry principle (which applies to kinetic theory and transient hydrodynamics), it is possible to place rigorous bounds on phase velocities, eigenmode convergence radii, spectral gaps, and equilibration rates in any inertial frame, using only information about the rest frame spectrum at zero wavenumber. The conventional intuition coming from time dilation is also shown to lead to generically wrong predictions, but becomes accurate if the fluid is non-relativistic in the rest frame.

2601.03081Jan 2026

View

Revisiting Spherically Symmetric Spacetime I: Geometro-Hydrodynamics

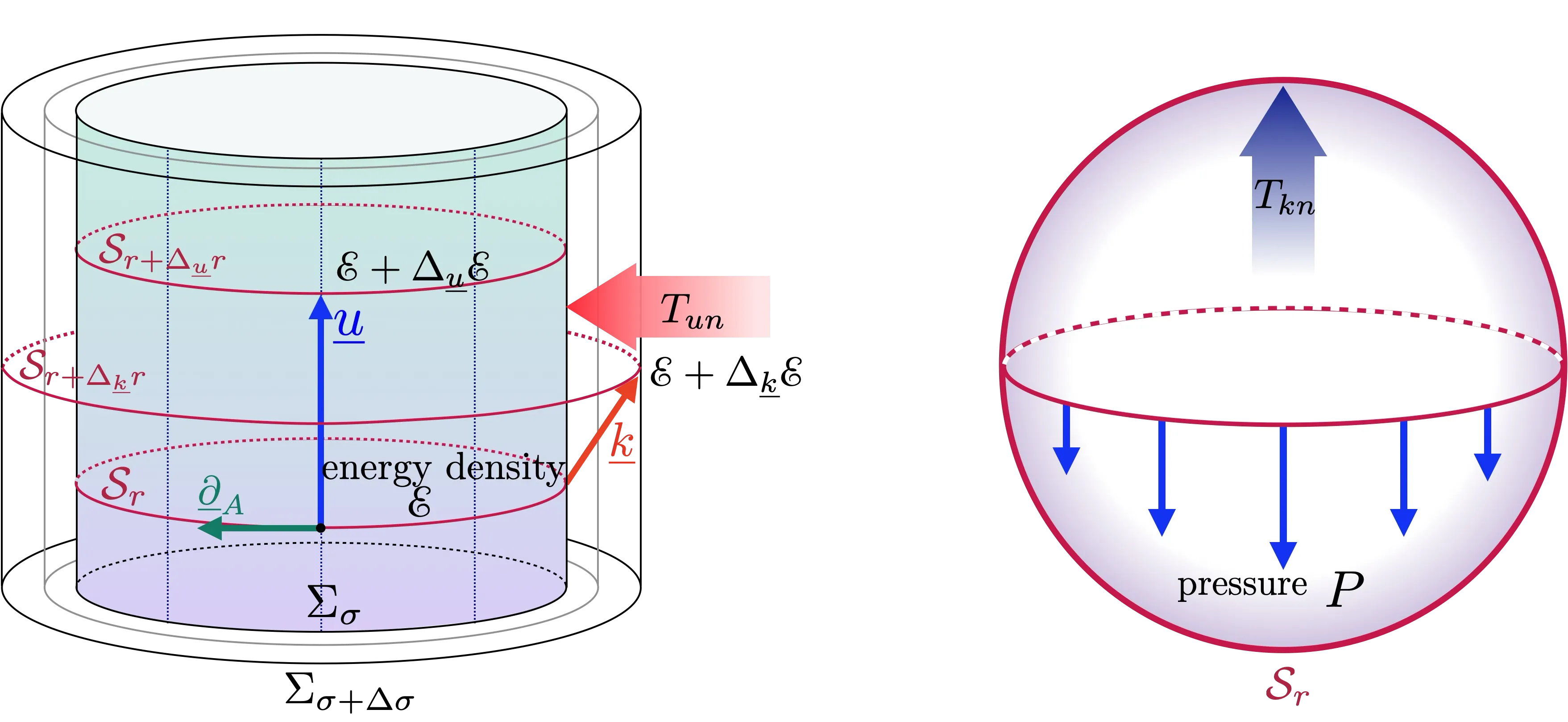
This series of works revisits the geometry, dynamics, and covariant phase space of spherically symmetric spacetimes with the aim of exploring the thermodynamics of spacetime from their dynamical properties. In this first paper, we examine the geometry from the perspective of a foliation by spherical hypersurfaces. Using the rigging technique, we first define a local frame adapted to these slices and reconstruct the geometry and dynamics fully. We clarify the connection of the frame adapted to constant-radius slices, to the Kodama vector and Misner-Sharp energy. Through frame transformations, we then show that the gravitational dynamics in a general foliation-adapted frame can be interpreted as hydrodynamics, i.e., geometro-hydrodynamics: the Einstein equations exhibit the gravitational analogs of the Euler and Young-Laplace equations, and the spacetime can be viewed as the worldvolume of a concentric stack of "gravitational bubbles" -- spherical collective modes with the Misner-Sharp energy density and a geometric pressure. We apply this framework to apparent horizons and study the dynamics. Finally, we demonstrate that a similar geometro-hydrodynamic picture holds in Lovelock gravity. These results provide a fresh perspective on this class of spacetimes and lay the foundation for understanding their thermodynamic properties.

2601.03077Jan 2026

View

Does relativistic motion really freeze initially maximal entanglement?

We investigate the relativistic dynamics of quantum entanglement in a four-qubit cluster ($CL_4$) state using a fully operational Unruh-DeWitt detector framework. Contrary to the widely held expectation that the Unruh effect inevitably degrades initially maximal entanglement, we demonstrate that the 1-3 bipartite entanglement of the $CL_4$ state remains strictly maximal for all accelerations, including the infinite-acceleration limit. This result uncovers a previously unexplored phenomenon, namely the ``complete freezing of initially maximal entanglement" under relativistic motion. To the best of our knowledge, this is the first identification and systematic characterization of such a phenomenon within a relativistic framework. These findings overturn the conventional view that acceleration universally diminishes maximal entanglement and establish the $CL_4$ state as a promising resource for quantum information processing in non-inertial or curved-spacetime settings.

2601.02976Jan 2026

View

Page 1 of 166