Trending in High Energy Physics - Theory
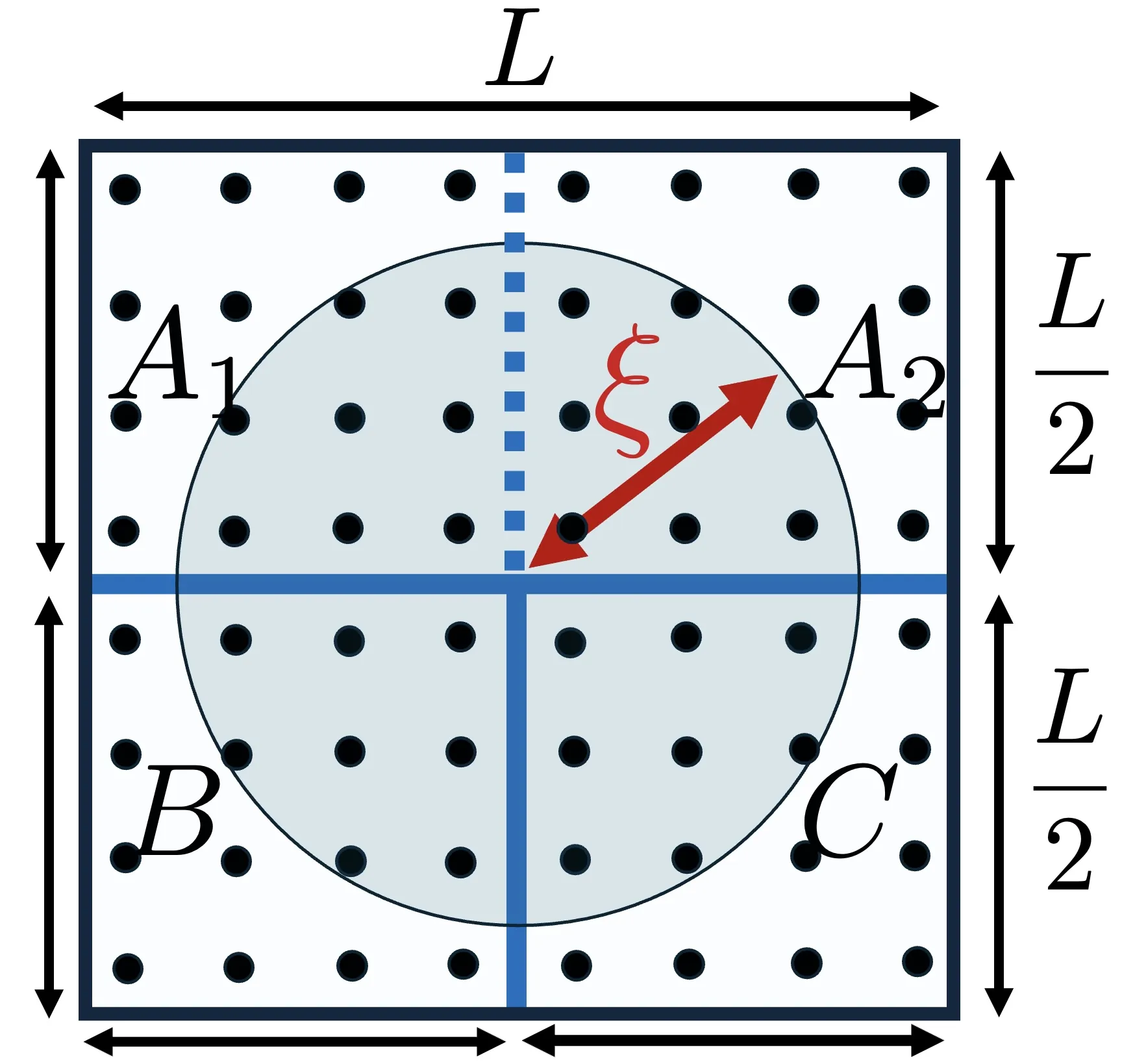
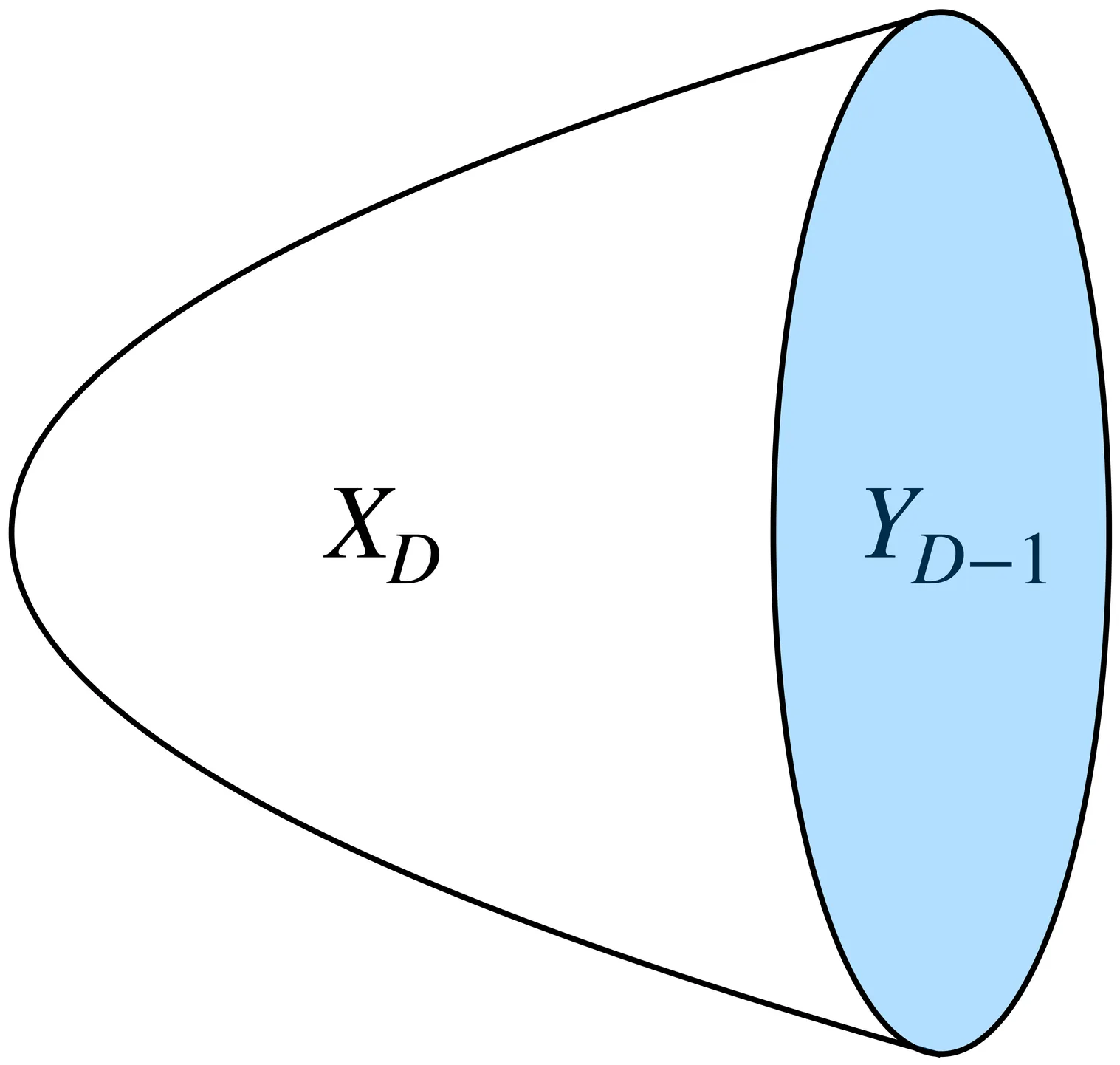
Where Multipartite Entanglement Localizes: The Junction Law for Genuine Multi-Entropy
We uncover a "junction law" for genuine multipartite entanglement, suggesting that in gapped local systems multipartite entanglement is controlled and effectively localized near junctions where subsystem boundaries meet. Using the Rényi-2 genuine multi-entropy $\mathrm{GM}^{(\mathtt{q})}_2$ as a diagnostic of genuine $\mathtt{q}$-partite entanglement, we establish this behavior in $(2+1)$-dimensional gapped free-fermion lattices with correlation length $ξ$. For partitions with a single junction, $\mathrm{GM}^{(\mathtt{q})}_2$ exhibits a universal scaling crossover in $L/ξ$, growing for $L\llξ$ and saturating to a $ξ$-dependent constant for $L\ggξ$, up to $\mathcal{O}(e^{-L/ξ})$ corrections. In sharp contrast, for partitions without a junction, $\mathrm{GM}^{(\mathtt{q})}_2$ is exponentially suppressed in $L/ξ$ and drops below numerical resolution once $L\ggξ$. We observe the same pattern for $\mathtt{q}=3$ (tripartite) and $\mathtt{q}=4$ (quadripartite) cases, and further corroborate this localization by translating the junction at fixed system size. We also provide a geometric explanation of the junction law in holography. Altogether, these results show that in this gapped free-fermion setting genuine multipartite entanglement is localized within a correlation-length neighborhood of junctions.
2602.16331
Feb 2026High Energy Physics - Theory
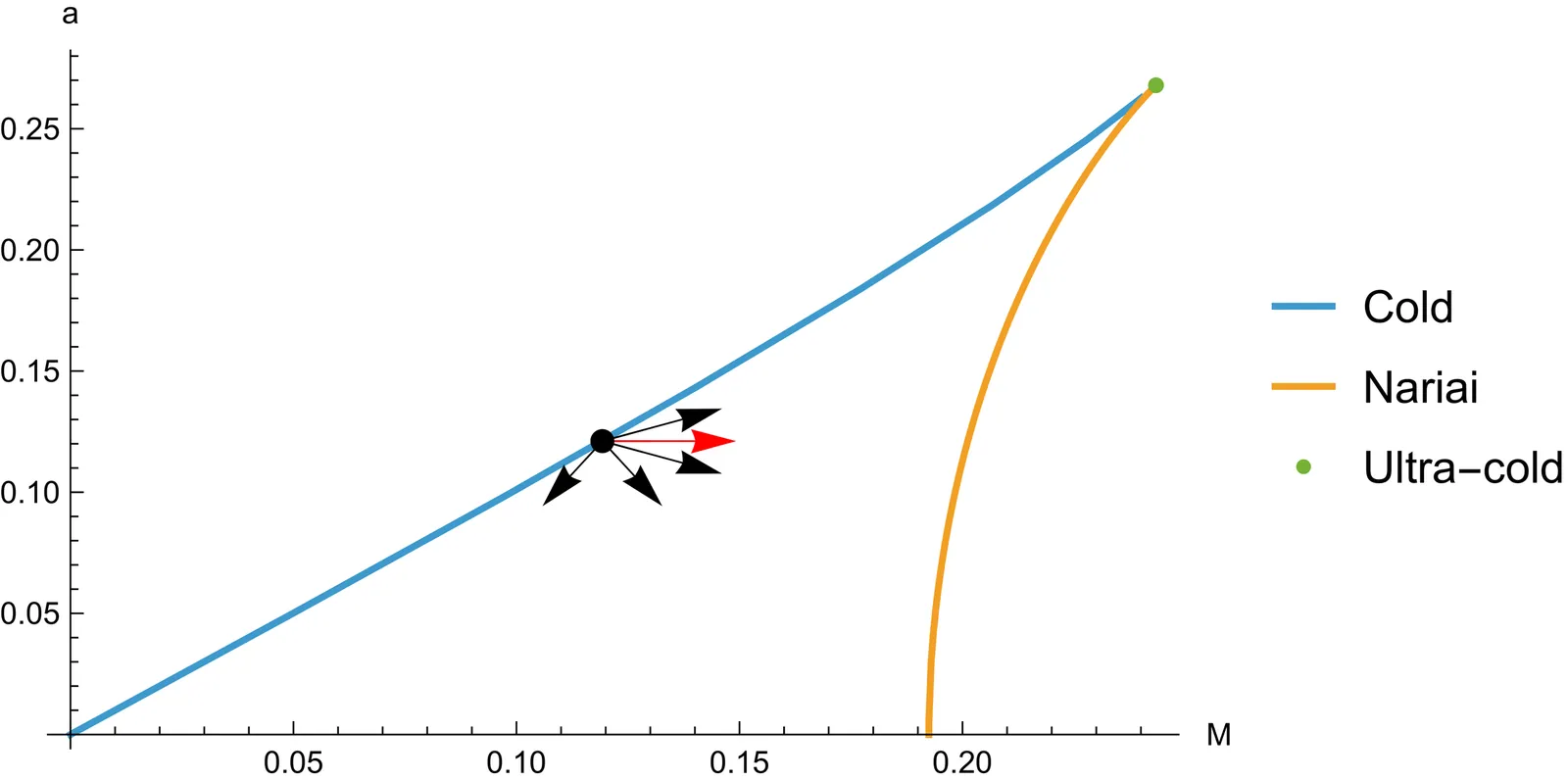
Toward a mathematically consistent theory of semiclassical gravity or, How to have your wormholes and factorize, too
We review three well known inconsistencies in the standard mathematical formulation of semiclassical gravity: the factorization problem, the information problem, and the closed universe problem. Building upon recent work, we explore how modifying the holographic dictionary may provide the necessary freedom to resolve these three problems in a unified manner while maintaining more well established aspects of the standard correspondence. Using the modified holographic dictionary as a scaffolding, we propose a program for constructing an `extended' semiclassical gravitational path integral which (i) is manifestly factorizing, (ii) computes a von Neumann entropy which satisfies the Page curve, and (iii) incorporates new operators that create closed baby universe states. Our construction may be interpreted as imposing a semiclassical version of background independence/a no global symmetry condition, defining a modified large N limit, preparing an ensemble of dual theories, or enforcing observer rules using gravitational degrees of freedom.
2602.15120
Feb 2026High Energy Physics - Theory
 2602.12176
2602.12176Single-minus gluon tree amplitudes are nonzero
Single-minus tree-level $n$-gluon scattering amplitudes are reconsidered. Often presumed to vanish, they are shown here to be nonvanishing for certain "half-collinear" configurations existing in Klein space or for complexified momenta. We derive a piecewise-constant closed-form expression for the decay of a single minus-helicity gluon into $n-1$ plus-helicity gluons as a function of their momenta. This formula nontrivially satisfies multiple consistency conditions including Weinberg's soft theorem.
2602.12176
Feb 2026High Energy Physics - Theory
 2602.11254
2602.11254Quantum Gravity on AdS$_3\times$S$^3$ from CFT: Bootstrapping $n=21$
We consider the simplest four-point scattering amplitude of $SO(n)$ tensor multiplets in six-dimensional (2,0) supergravity on AdS$_3\times$S$^3$. Using crossing symmetry and the consistency of the operator product expansion in the dual CFT, we explicitly construct the one-loop contribution to the correlator at order $1/c^2$, both in position space and in Mellin space. We show that a strong form of the bootstrap equations imposes constraints on the value of $n$. Remarkably, we find that our bootstrap approach uniquely determines $n=21$, which corresponds to the spectrum of IIB string theory compactified on K3. This stands in sharp contrast to the tree-level correlator for which $n$ is unconstrained. We also analyse the spectrum of unprotected double-trace operators and solve the mixing problem in the first case that involves both tensor and graviton correlators. When $n=21$, the anomalous dimensions rationalise and one of them vanishes. Lastly, we study the flat-space limit of the correlator and find perfect agreement with the one-loop amplitude recently obtained in [arXiv:2510.24558].
2602.11254
Feb 2026High Energy Physics - Theory
Probing holographic conformal field theories
We introduce an operational, boundary-first framework that embeds relativistic quantum-information protocols into anti-de Sitter/Conformal Field Theory (AdS/CFT) by coupling an Unruh--DeWitt detector directly to a local scalar primary operator of a holographic CFT. Using the universal CFT Wightman function, we compute the detector's reduced density operator perturbatively, retaining both excitation probabilities and coherences. As a concrete resource-theoretic application, we implement magic resource (mana) harvesting with a qutrit probe. For a CFT dual to global AdS, we show that the harvested mana sharply distinguishes the two admissible scalar quantizations in the Breitenlohner--Freedman window, with the standard quantization yielding systematically larger mana than the alternate one. Our results provide a viable way of testing holography principle through quantum information resource.
2602.07895
Feb 2026High Energy Physics - Theory
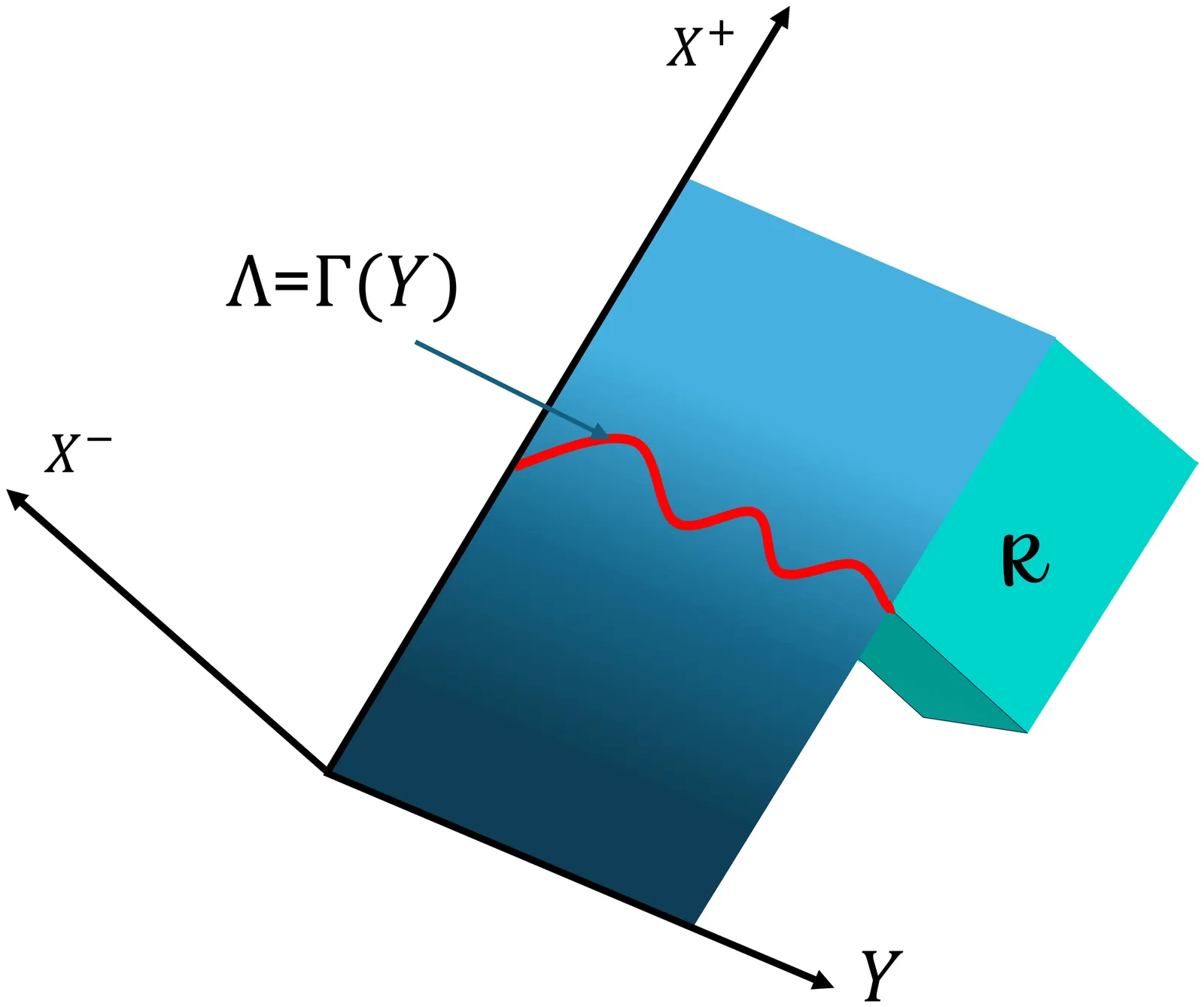
Towards a Proof of the Improved Quantum Null Energy Condition
The Improved Quantum Null Energy Condition (INEC) was recently derived from the (restricted) quantum focusing conjecture (QFC), and is a statement about the energy-momentum tensor (EMT) of field theories in Minkowski space-time. It is a stronger condition than the quantum null energy condition (QNEC), and includes the possibility of expanding or contracting geodesics. Using the properties of relative entropy and modular Hamiltonian associated with null deformation of the sphere, we show the INEC holds under an additional assumption relating the EMT to the relative entropy. Furthermore, using the QNEC and INEC as a basis, we briefly speculate about a possible modified Quantum Focusing Conjecture.
2601.18860
Jan 2026High Energy Physics - Theory
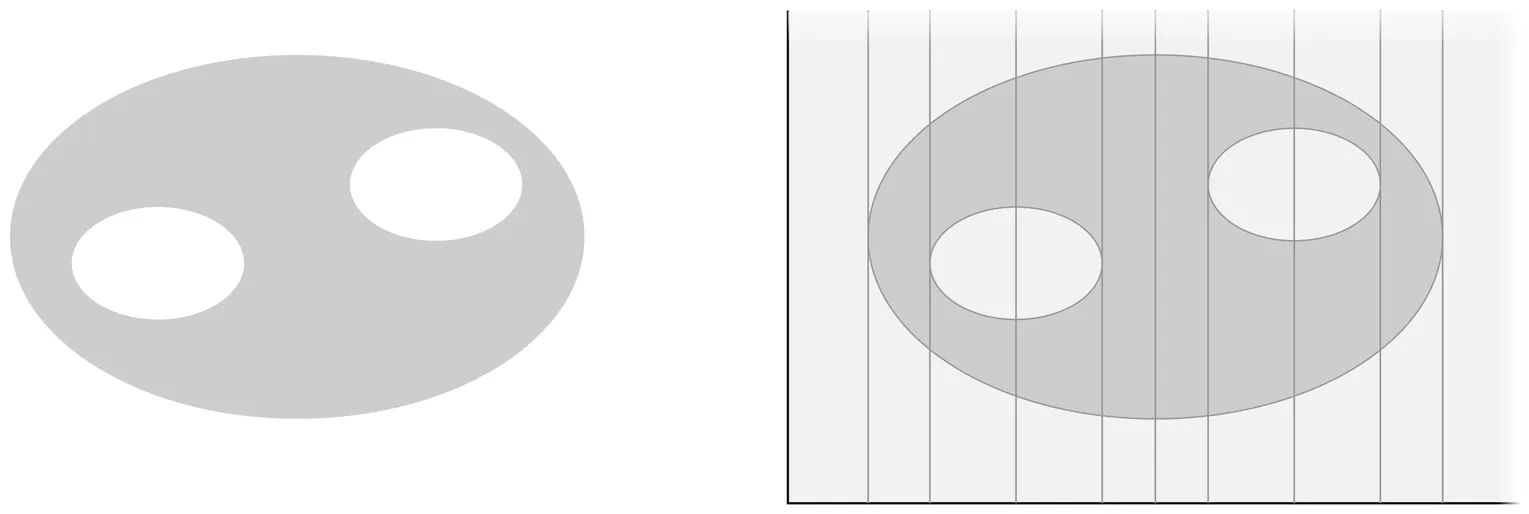
Tame Complexity of Effective Field Theories in the Quantum Gravity Landscape
Effective field theories consistent with quantum gravity obey surprising finiteness constraints, appearing in several distinct but interconnected forms. In this work we develop a framework that unifies these observations by proposing that the defining data of such theories, as well as the landscape of effective field theories that are valid at least up to a fixed cutoff, admit descriptions with a uniform bound on complexity. To make this precise, we use tame geometry and work in sharply o-minimal structures, in which tame sets and functions come with two integer parameters that quantify their information content; we call this pair their tame complexity. Our Finite Complexity Conjectures are supported by controlled examples in which an infinite Wilsonian expansion nevertheless admits an equivalent finite-complexity description, typically through hidden rigidity conditions such as differential or recursion relations. We further assemble evidence from string compactifications, highlighting the constraining role of moduli space geometry and the importance of dualities. This perspective also yields mathematically well-defined notions of counting and volume measures on the space of effective theories, formulated in terms of effective field theory domains and coverings, whose finiteness is naturally enforced by the conjectures.
2601.18863
Jan 2026High Energy Physics - Theory
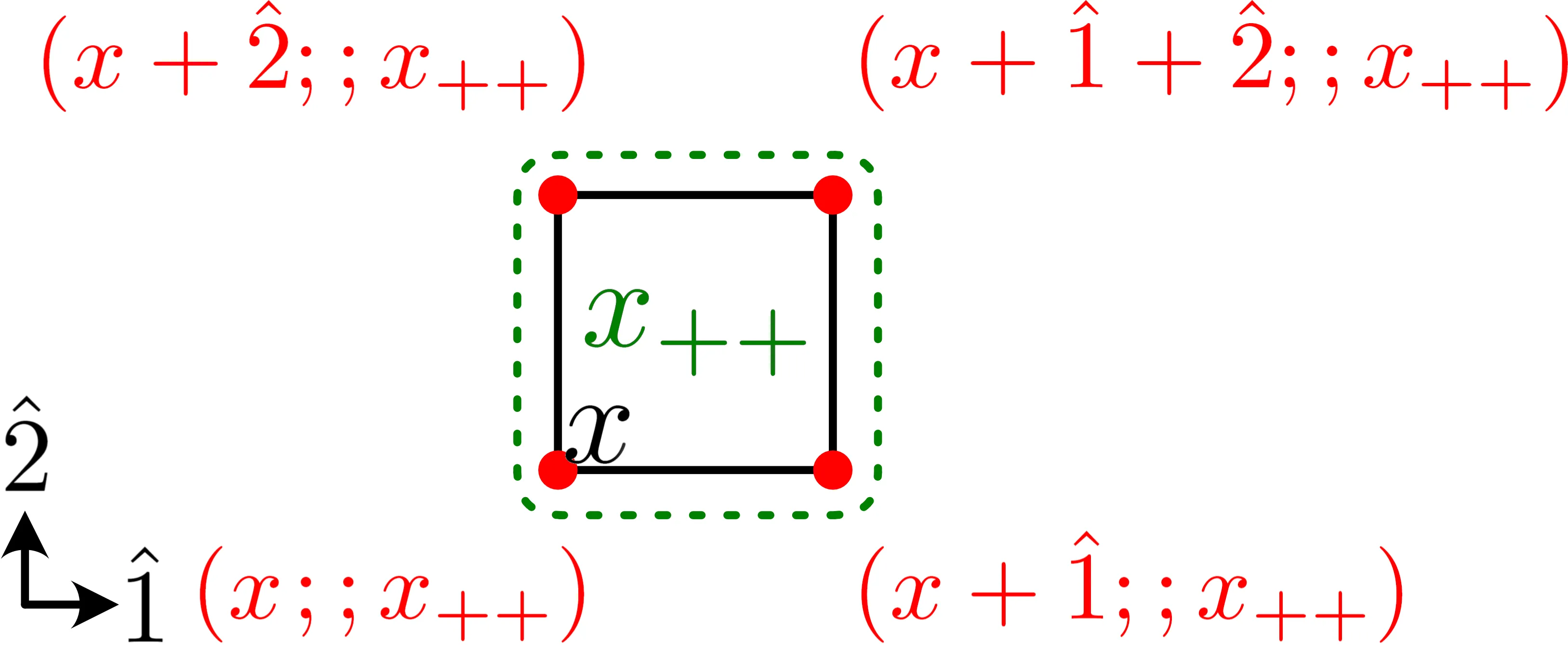
A Lattice U(1) Chern-Simons Theory via Lattice Deligne-Beilinson Cohomology
We define Deligne-Beilinson (DB) cohomology on a cubic lattice and use it to formulate and analyze lattice $U(1)$ Chern-Simons theory at even levels. The continuum DB cohomology provides a refined mathematical framework for continuum $U(1)$ connections constructed in a patchwise manner. The lattice DB cohomology we construct retains many essential properties of the continuum DB cohomology and naturally incorporates a notion of self-linking number. The lattice $U(1)$ Chern-Simons action formulated using the lattice DB cohomology is expressed as a simple quadratic form via the star product, which naturally exhibits level quantization. Framed Wilson lines respecting staggered symmetry are defined in a gauge-invariant manner, and their expectation values are shown to be given by the self-linking number, as follows from completing the square. Using the lattice Hodge decomposition, we explicitly characterize the DB cohomology on a three-dimensional cubic toroidal lattice and present a gauge-fixed, rigorous path integral for the lattice Chern-Simons theory. To regulate divergences in the lattice Chern-Simons path integral arising from staggered symmetry, we introduce a small Maxwell term. The resulting error is controlled by the linear order in the small Maxwell coupling.
2601.15939
Jan 2026High Energy Physics - Theory
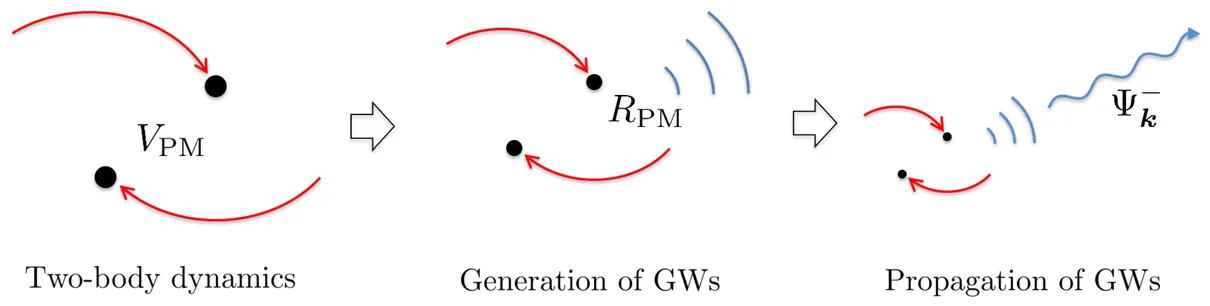
Resumming Scattering Amplitudes for Waveforms
We develop a formalism to compute non-perturbative 5-point scattering amplitudes and apply it to gravitational waveforms in the two-body problem for arbitrary trajectories. Drawing inspiration from Feshbach's projector formalism in nuclear physics, we introduce effective potentials governing graviton emission and relate them to perturbative scattering amplitudes at arbitrary order in the gravitational coupling and mass ratio. Once these potentials are determined, the corresponding non-perturbative amplitudes in the classical limit are obtained by iterative insertions and subsequently translated into gravitational waveforms using the KMOC formalism. As an application, we compute the gravitational waveform emitted by a two-body system moving along a generic, potentially highly bent, trajectory. Importantly, our formalism extends effective field theory matching of the gravitational two-body potential to radiative phenomena, enabling the extraction of gravitational-wave source terms directly from perturbative on-shell scattering amplitudes.
2601.08252
Jan 2026High Energy Physics - Theory
 2601.07906
2601.07906A universal sum over topologies in 3d gravity
We explore the sum over topologies in AdS$_3$ quantum gravity and its relationship with the statistical interpretation of the boundary theory. We formulate a statistical version of the conformal bootstrap that systematizes the universal statistical properties of high-energy CFT$_2$ data. We identify a series of surgery moves on bulk manifolds that precisely reflect the requirements of typicality and crossing symmetry of the boundary ensemble. These surgery moves generate a large number of bulk manifolds that have to be included in any reasonable definition of the gravitational path integral. We show that this procedure generates only on-shell (hyperbolic) manifolds, although it does not produce all of them. These proofs rely on structure theorems of 3-manifolds, which non-trivially interact with the requirements of the statistical boundary ensemble. We illustrate the application of this procedure with many examples, such as Euclidean wormholes, twisted $I$-bundles and handlebody-knots. Our findings reveal a large space of possible choices of which manifolds can be included in the gravitational path integral, reflecting a wide range of possible statistical ensembles consistent with crossing symmetry and typicality.
2601.079061
Jan 2026High Energy Physics - Theory
A melonic quantum mechanical model without disorder
We consider a quantum mechanical model involving interacting fermions without disorder that has the same low energy physics as the supersymmetric SYK model. The model is $SU(2)$ invariant, and the supercharge involves the $ SU(2) $ 3j symbol. We analyze various solvable corners, conceptually explain why it has a melonic expansion, and perform an exact diagonalization for small values of $N$. Expanded around the states with maximal angular momentum, the model is approximated by a two dimensional CFT. The BPS states have a simple description in that regime.
2601.08908
Jan 2026High Energy Physics - Theory
Extended Heun Hierarchy in Quantum Seiberg-Witten Geometry
We investigate the quantum geometry of the Seiberg-Witten curve for $\mathcal{N}=2$, $\mathrm{SU(2)}^n$ linear quiver gauge theories. By applying the Weyl quantization prescription to the algebraic curve, we derive the corresponding second-order differential equation and demonstrate that it is isomorphic to the Extended Heun Equation with $n+3$ regular singular points. The physical parameters of the gauge theory are linked to the canonical coefficients of the Heun equation via a polynomial representation of the Seiberg-Witten curve. This framework provides the necessary mathematical foundation to apply non-perturbative gauge-theoretic techniques, such as instanton counting, to spectral problems in gravitational physics, most notably for higher-dimensional black holes.
2601.05204
Jan 2026High Energy Physics - Theory
Integrable Systems
These notes are based on lecture courses I gave to third year mathematics students at Cambridge. They could form a basis of an elementary one--term lecture course on integrable systems covering the Arnold-Liouville theorem, inverse scattering transform, Hamiltonian methods in soliton theory and Lie point symmetries. No knowledge beyond basic calculus and ordinary differential equation is assumed.
2601.04077
Jan 2026High Energy Physics - Theory
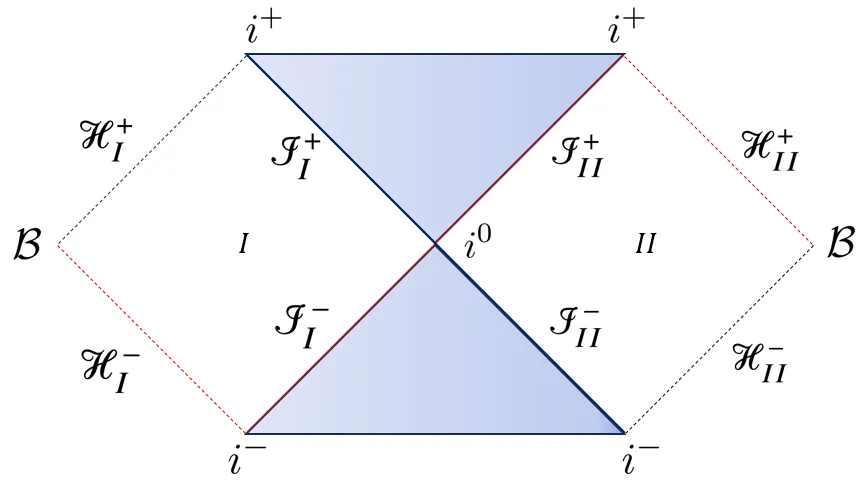
Black hole thermodynamics at null infinity. Part 2: Open systems, Markovian dynamics and work extraction from non-rotating black holes
Black hole thermodynamics provides a unique setting in which general relativity, quantum field theory, and statistical mechanics converge. In semiclassical gravity, this interplay culminates in the generalized second law (GSL), whose modern proofs rely on information theoretic techniques applied to algebras of observables defined on null hypersurfaces. These proofs exhibit close structural parallels with the thermodynamics of open quantum systems governed by Markovian dynamics. In this work, we draw parallels between the dynamics of quantum fields in regions bounded by non expanding causal horizons and the thermodynamics of quantum systems weakly coupled to equilibrium reservoirs. We introduce a dictionary relating late time boundary conditions to the choice of reservoir, vacuum states to fixed points of the dynamics, and modular Hamiltonians to thermodynamic potentials. Building on results from a companion paper on dual generalized second laws at future null infinity, we show that additional terms appearing in the associated thermodynamic potentials admit a natural interpretation as work contributions. We demonstrate that certain non thermal vacuum states at null infinity allow for the operation of autonomous thermal engines and enable work extraction from the radiation. Extending the analysis to the Unruh vacuum in Schwarzschild and Kerr backgrounds, we obtain generalized grand potential type laws incorporating grey body effects and angular momentum fluxes. Altogether, our results clarify the thermodynamic description of black hole dynamics and place it within the broader framework of open quantum thermodynamics.
2601.03356
Jan 2026High Energy Physics - Theory
$2+2=4$
Motivated by the observation that $2+2=4$, we consider four-dimensional $\mathcal{N}=2$ superconformal field theories on $S^2\timesΣ$, turning on a suitable rigid supergravity background. On the one hand, reduction of a four-dimensional theory ${T}$ on a Riemann surface $Σ$ leads to a family $\mathscr{F}[{T}, Σ]$ of two-dimensional $(2,2)$ unitary SCFTs, a two-dimensional analog of the four-dimensional theories of class $\mathscr{S}$. On the other hand, reduction on $S^2$ yields a non-unitary two-dimensional CFT $\mathscr{C}[{T}]$ whose chiral algebra is the same as the one associated to ${T}$ by the standard SCFT/VOA correspondence. This construction upgrades the vertex operator algebra to a full-fledged two-dimensional CFT. What's more, it leads to a novel 2d/2d correspondence, a "$2+2 = 4$" analog of the "$4+2=6$" AGT correspondence: the $S^2$ partition function of $\mathscr{F}[{T}; Σ]$ is computed by correlation functions of $\mathscr{C}[{T}]$ on $Σ$. The elliptic genus of $\mathscr{F}[{T}; Σ]$ is instead computed by a topological QFT $\mathscr{E}[T]$ on $Σ$. A central question is whether one can give a purely two-dimensional presentation of the family $\mathscr{F}[{T}; Σ]$ of $(2, 2)$ theories. We propose an algorithm to realize the $(2, 2)$ theories as gauged linear sigma models when ${T}$ is an Argyres-Douglas theory of type $(A_1, A_{2k})$ and $Σ$ an $n$-punctured sphere. We perform stringent checks of our conjecture for $k=1$ and $k=2$.
2601.00058
Dec 2025High Energy Physics - Theory
 2601.00605
2601.00605Effective field theory for dissipative photons from higher-form symmetries
Recent developments in generalized symmetries have provided new insights into quantum field theories. Within this framework, photons can be understood as Nambu-Goldstone modes associated with a spontaneously broken higher-form symmetry. In this work, we develop an effective field theory that builds on this symmetry structure to describe the real-time dynamics of photons in insulating media at finite temperature. Combining the Schwinger-Keldysh formalism with the generalized coset construction, we formulate a symmetry-based effective action that incorporates both conservative and dissipative effects. The effective theory implements the dynamical Kubo-Martin-Schwinger symmetry, ensuring consistency with the fluctuation-dissipation relation and Onsager's reciprocal relations. Within this framework, we derive the entropy current associated with dissipative photon dynamics and demonstrate the non-negativity of its divergence, in accordance with the second law of thermodynamics. We also clarify the symmetry origin of the gauge redundancy in the unbroken phase within the Schwinger-Keldysh framework, relating it to strong and weak realizations of higher-form symmetries. Our results provide a model-independent effective description of photon dynamics in insulating media at finite temperature.
2601.00605
Jan 2026High Energy Physics - Theory
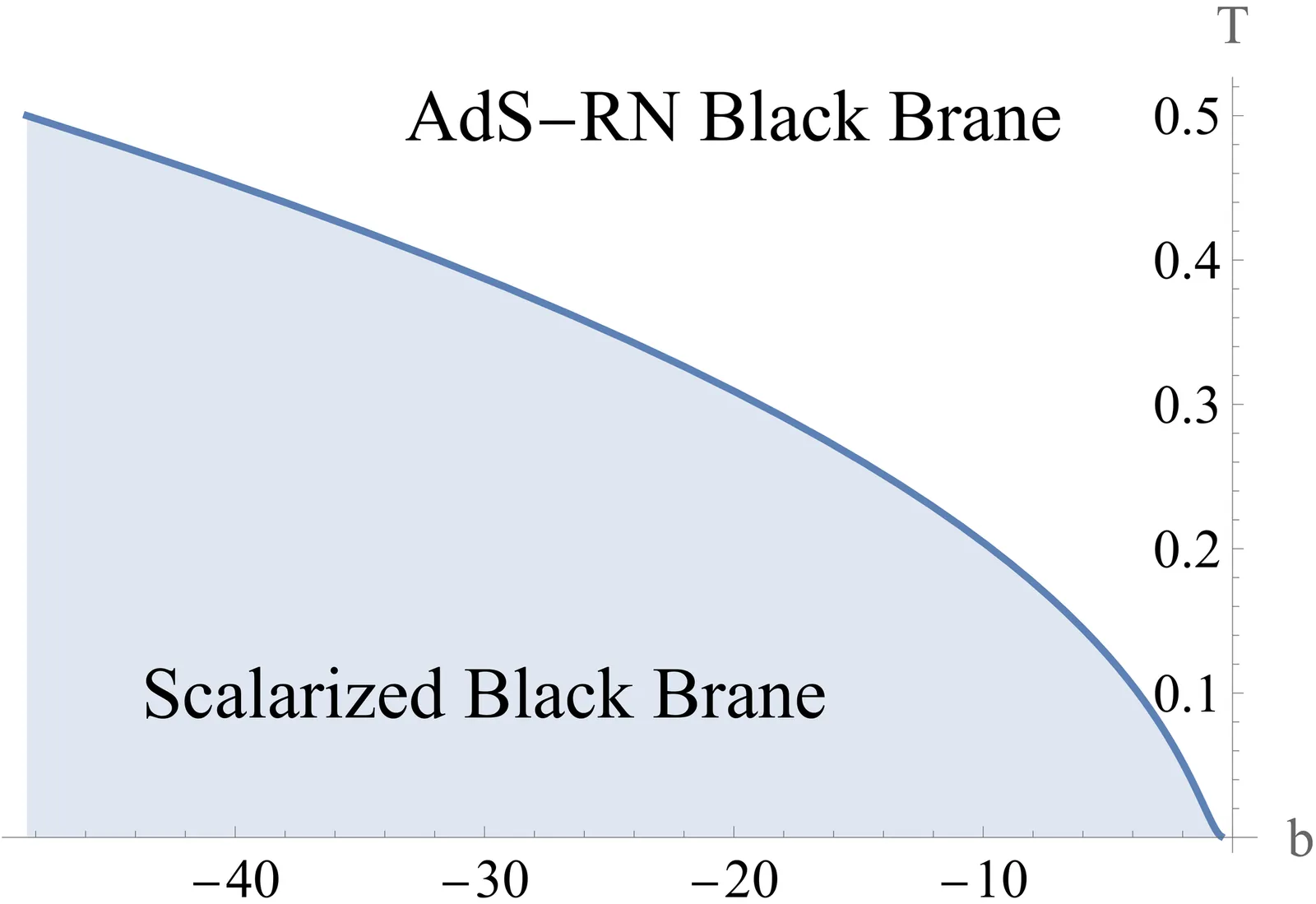
Diagnosing Critical Behavior in AdS Einstein-Maxwell-Scalar Theory via Holographic Entanglement Measures
We investigate the holographic mixed-state entanglement measures in the Einstein-Maxwell-Scalar (EMS) theory. Several quantities are computed, including the holographic entanglement entropy (HEE), mutual information (MI), entanglement wedge cross-section (EWCS), and butterfly velocity ($v_B$). Our findings demonstrate that these measures can effectively diagnose phase transitions. Notably, EWCS and MI, as mixed-state entanglement measures, exhibit behavior opposite to that of the HEE. Additionally, we study the butterfly velocity, a dynamic quantum information measure, and observe that it behaves differently from the static quantum information measures. We propose that the butterfly velocity is initially dominated by entanglement and subsequently by thermal entropy as the coupling constant increases. Moreover, we examine the scaling behavior of the holographic entanglement measures and find that all the critical exponents are equal to $1$, which is twice that of the scalar field. We also explore the inequality between EWCS and MI, noting that the growth rate of MI consistently exceeds that of EWCS during phase transitions. These features are expected to be universal across thermodynamic phase transitions, with the inequalities becoming more significant as one moves away from the critical point.
2601.00069
Dec 2025High Energy Physics - Theory
 2601.00662
2601.00662Extended BMS representations and strings
We construct in detail the irreducible representations of the BMS group with super rotations in three and four dimensions that have the same rest frame momenta as the massive and massless Poincare point particles. We compare these representations to those of the Poincare group and also to the analogous representations of global BMS. We argue that these extended BMS representations are carried by a string rather than a point particle. The super rotations play a crucial role in our discussions.
2601.00662
Jan 2026High Energy Physics - Theory