Quantum Physics

Quantum mechanics, quantum information, and quantum computing

Trending in Quantum Physics

Who can compete with quantum computers? Lecture notes on quantum inspired tensor networks computational techniques

This is a set of lectures on tensor networks with a strong emphasis on the core algorithms involving Matrix Product States (MPS) and Matrix Product Operators (MPO). Compared to other presentations, particular care has been given to disentangle aspects of tensor networks from the quantum many-body problem: MPO/MPS algorithms are presented as a way to deal with linear algebra on extremely (exponentially) large matrices and vectors, regardless of any particular application. The lectures include well-known algorithms to find eigenvectors of MPOs (the celebrated DMRG), solve linear problems, and recent learning algorithms that allow one to map a known function into an MPS (the Tensor Cross Interpolation, or TCI, algorithm). The lectures end with a discussion of how to represent functions and perform calculus with tensor networks using the "quantics" representation. They include the detailed analytical construction of important MPOs such as those for differentiation, indefinite integration, convolution, and the quantum Fourier transform. Three concrete applications are discussed in detail: the simulation of a quantum computer (either exactly or with compression), the simulation of a quantum annealer, and techniques to solve partial differential equations (e.g. Poisson, diffusion, or Gross-Pitaevskii) within the "quantics" representation. The lectures have been designed to be accessible to a first-year PhD student and include detailed proofs of all statements.

2601.03035

Jan 2026Quantum Physics

(PhD Thesis) The Information Locally Stored in Quantum Fields: From Entanglement to Gravity

This is an updated version of my PhD thesis, defended at the University of Waterloo on the 2nd of April 2025, uploaded to the ArXiv with the goal of reaching a wider audience. The thesis is divided into 5 chapters, respectively containing (I) a brief introduction to local quantum field theory (QFT), (II) a description of local probes in QFT, (III) a discussion of entanglement in QFT and how to probe it, (IV) a description of the regimes where QFT interactions can be approximated by direct interactions, and (V) a discussion the information about the geometry of spacetime contained in quantum fields. The partial goal of this thesis is to serve as a guide for students aiming to tackle these different research programs. If the reader is interested in pursuing one or more research projects detailed here, they are encouraged to contact me for collaboration in these topics.

2601.00128

Dec 2025Quantum Physics

The Maximal Entanglement Limit in Statistical and High Energy Physics

These lectures advocate the idea that quantum entanglement provides a unifying foundation for both statistical physics and high-energy interactions. I argue that, at sufficiently long times or high energies, most quantum systems approach a Maximal Entanglement Limit (MEL) in which phases of quantum states become unobservable, reduced density matrices acquire a thermal form, and probabilistic descriptions emerge without invoking ergodicity or classical randomness. Within this framework, the emergence of probabilistic parton model, thermalization in the break-up of confining strings and in high-energy collisions, and the universal small $x$ behavior of structure functions arise as direct consequences of entanglement and geometry of high-dimensional Hilbert space.

2601.00405

Jan 2026Quantum Physics

Chaos and thermalization in Clifford-Floquet dynamics

We study the ergodic properties of a unitary Floquet dynamics arising from the repeated application of a translationally-invariant Clifford Quantum Cellular Automata to an infinite system of qubits in d dimensions. One expects that if the QCA does not exhibit any periodicity, a generic initial state of qubits will thermalize, that is, approach the infinite-temperature state. We show that this is true for many classes of states, both pure and mixed. In particular, this is true for all initial states that are short-range entangled and close to the equilibrium state. We also point out a subtle distinction between weak and strong thermalization.

2601.00511

Jan 2026Quantum Physics

Nature is stingy: Universality of Scrooge ensembles in quantum many-body systems

Recent advances in quantum simulators allow direct experimental access to the ensemble of pure states generated by measuring part of an isolated quantum many-body system. These projected ensembles encode fine-grained information beyond thermal expectation values and provide a new window into quantum thermalization. In chaotic dynamics, projected ensembles exhibit universal statistics, a phenomenon known as deep thermalization. While infinite-temperature systems generate Haar-random ensembles, realistic physical constraints such as finite temperature or conservation laws require a more general framework. It has been proposed that deep thermalization is governed in general by the emergence of Scrooge ensembles, maximally entropic distributions of pure states consistent with the underlying constraints. Here we provide rigorous arguments supporting this proposal. To characterize this universal behavior, we invoke Scrooge $k$-designs, which approximate Scrooge ensembles, and identify three physically distinct mechanisms for their emergence. First, global Scrooge designs can arise from long-time chaotic unitary dynamics alone, without the need for measurements. Second, if the global state is highly scrambled, a local Scrooge design is induced when the complementary subsystem is measured. Third, a local Scrooge ensemble arises from an arbitrary entangled state when the complementary system is measured in a highly scrambled basis. Numerical simulations across a range of many-body systems identify coherence, entanglement, non-stabilizerness, and information scrambling as essential resources for the emergence of Scrooge-like behavior. Taken together, our results establish a unified theoretical framework for the emergence of maximally entropic, information-stingy randomness in quantum many-body systems.

2601.002661

Jan 2026Quantum Physics

Exponentially Accelerated Sampling of Pauli Strings for Nonstabilizerness

Quantum magic, quantified by nonstabilizerness, measures departures from stabilizer structure and underlies potential quantum speedups. We introduce an efficient classical algorithm that exactly computes stabilizer Rényi entropies and stabilizer nullity for generic many-body wavefunctions of $N$ qubits. The method combines the fast Walsh-Hadamard transform with an exact partition of Pauli operators. It achieves an exponential speedup over direct approaches, reducing the average cost per sampled Pauli string from $O(2^N)$ to $O(N)$. Building on this framework, we further develop a Monte-Carlo estimator for stabilizer Rényi entropies together with a Clifford-based variance-reduction scheme that suppresses sampling fluctuations. We benchmark the accuracy and efficiency on ensembles of random magic states, and apply the method to random Clifford circuits with doped $T$ gates, comparing different doping architectures. Our approach applies to arbitrary quantum states and provides quantitative access to magic resources both encoded in highly entangled states and generated by long-time nonequilibrium dynamics.

2601.00761

Jan 2026Quantum Physics

Exponential-to-polynomial scaling of measurement overhead in circuit knitting via quantum tomography

Circuit knitting is a family of techniques that enables large quantum computations on limited-size quantum devices by decomposing a target circuit into smaller subcircuits. However, it typically incurs a measurement overhead exponential in the number of cut locations, and it remains open whether this scaling is fundamentally unavoidable. In conventional circuit-cutting approaches based on the quasiprobability decomposition (QPD), for example, rescaling factors lead to an exponential dependence on the number of cuts. In this work, we show that such an exponential scaling is not universal: it can be circumvented for tree-structured quantum circuits via concatenated quantum tomography protocols. We first consider estimating the expectation value of an observable within additive error $ε$ for a tree-structured circuit with tree depth 1 (two layers), maximum branching factor $R$, and bond dimension at most $d$ on each edge. Our approach uses quantum tomography to construct, for each cut edge, a local decomposition that eliminates the rescaling factors in conventional QPD, instead introducing a controllable bias set by the tomography sample size. After cutting $R$ edges, we show that $\mathcal{O}(d^3R^3\ln(dR)/ε^2)$ total measurements suffice, including tomography cost. Next, we extend the tree-depth-1 case to general trees of depth $L\geq2$, and give an algorithm whose total measurement cost $\tilde{\mathcal{O}}(d^3K^{5}/ε^2)$ scales polynomially with the number of cuts for complete $R$-ary trees. Finally, we perform an information-theoretic analysis to show that, in a comparable tree-depth-1 setting, conventional QPD-based wire-cutting methods require at least $Ω((d+1)^R/ε^2)$ measurements. This exponential separation highlights the significance of tomography-based construction for reducing measurement overhead in hybrid quantum-classical computations.

2512.19623

Dec 2025Quantum Physics

Magic state cultivation on a superconducting quantum processor

Fault-tolerant quantum computing requires a universal gate set, but the necessary non-Clifford gates represent a significant resource cost for most quantum error correction architectures. Magic state cultivation offers an efficient alternative to resource-intensive distillation protocols; however, testing the proposal's assumptions represents a challenging departure from quantum memory experiments. We present an experimental study of magic state cultivation on a superconducting quantum processor. We implement cultivation, including code-switching into a surface code, and develop a fault-tolerant measurement protocol to bound the magic state fidelity. Cultivation reduces the error by a factor of 40, with a state fidelity of 0.9999(1) (retaining 8% of attempts). Our results experimentally establish magic state cultivation as a viable solution to one of quantum computing's most significant challenges.

2512.139083

Dec 2025Quantum Physics

2512.12071

Proof of Spin-Statistics Theorem in Quantum Mechanics of Identical Particles

A nonrelativistic proof of the spin-statistics theorem is given in terms of the field operators satisfying commutation and anticommutation relations, which are introduced here in the coordinate space as a means to build the permutation symmetry into the brackets of identical particles. An eigenvalue problem of a $π$-rotation for a product of two annihilation operators is combined with an analysis on its rotational property to prove the connection that the field operators for integral-spin and half-integral-spin particles obey the commutation and anticommutation relations, respectively.

2512.12071

Dec 2025Quantum Physics

Tailored Error Mitigation for Single-Qubit Magnetometry

Quantum sensing is an emerging field with the potential to outperform classical methods in both precision and spatial resolution. However, the sensitivity of the underlying quantum platform also makes the sensors highly susceptible to their environmental noise. To address this issue, techniques from the field of quantum error mitigation use information about the noise to improve measurement results. We present a novel mitigation technique for quantum sensors to efficiently reverse the effects of any noise that can be described by a completely positive trace preserving map. The method leverages the knowledge acquired by a pre-characterization step of the device to automatically adapt to the complexity of the dissipative evolution and to indicate optimal sensing times $τ$ to achieve the most accurate results. We demonstrate that our method reaches the best achievable sensitivity in noisy single-NV-center magnetometry. This work marks a further step toward more resilient quantum sensors with the smallest scale of resolution.

2512.11671

Dec 2025Quantum Physics

Basis dependence of Neural Quantum States for the Transverse Field Ising Model

Neural Quantum States (NQS) are powerful tools used to represent complex quantum many-body states in an increasingly wide range of applications. However, despite their popularity, at present only a rudimentary understanding of their limitations exists. In this work, we investigate the dependence of NQS on the choice of the computational basis, focusing on restricted Boltzmann machines. Considering a family of rotated Hamiltonians corresponding to the paradigmatic transverse-field Ising model, we discuss the properties of ground states responsible for the dependence of NQS performance, namely the presence of ground state degeneracies as well as the uniformity of amplitudes and phases, carefully examining their interplay. We identify that the basis-dependence of the performance is linked to the convergence properties of a cluster or cumulant expansion of multi-spin operators -- providing a framework to directly connect physical, basis-dependent properties, to performance itself. Our results provide insights that may be used to gauge the applicability of NQS to new problems and to identify the optimal basis for numerical computations.

2512.116321

Dec 2025Quantum Physics

Spectral side channels in quantum key distribution under laser damage

In the transmitter of a quantum key distribution (QKD) system, a dense wavelength-division multiplexer (DWDM) is typically used to combine quantum and synchronization signals and is directly connected to the quantum channel. As a result, it becomes the first optical component exposed to laser-injection attacks. Therefore, understanding the behavior of DWDMs under such attacks is essential for assessing the practical security of QKD systems. In this work, we systematically investigate the characteristics of DWDMs under high-power laser illumination. Our experimental results show that certain DWDM samples exhibit pronounced changes in their spectral features once the injected laser power surpasses a specific threshold. Taking the Trojan-horse attack as an illustrative example, we further perform a theoretical analysis of the resulting spectral side channel and show that it can reduce the maximum secure transmission distance to below 66.9% of its original value. By combining experimental observations with theoretical modeling, this study advances the understanding of the influence of DWDMs on the practical security of QKD systems.

2512.11701

Dec 2025Quantum Physics

Boltzmann to Lindblad: Classical and Quantum Approaches to Out-of-Equilibrium Statistical Mechanics

Open quantum systems play a central role in contemporary nanoscale technologies, including molecular electronics, quantum heat engines, quantum computation and information processing. A major theoretical challenge is to construct dynamical models that are simultaneously consistent with classical thermodynamics and complete positivity. In this work, we develop a framework that addresses this issue by extending classical stochastic dynamics to the quantum domain. We begin by formulating a generalized Langevin equation in which both friction and noise act symmetrically on the two Hamiltonian equations. From this, we derive a generalized Klein-Kramers equation expressed in terms of Poisson brackets, and we show that it admits the Boltzmann distribution as its stationary solution while satisfying the first and second laws of thermodynamics along individual trajectories. Applying canonical quantization to this classical framework yields two distinct quantum master equations, depending on whether the friction operators are taken to be Hermitian or non-Hermitian. By analyzing the dynamics of a harmonic oscillator, we determine the conditions under which these equations reduce to a Lindblad-type generator. Our results demonstrate that complete positivity is ensured only when friction and noise are included in both Hamiltonian equations, thus fully justifying the classical construction. Moreover, we find that the friction coefficients must satisfy the same positivity condition in both the Hermitian and non-Hermitian formulations, revealing a form of universality that transcends the specific operator representation. The formalism offers a versatile tool for deriving quantum versions of the thermodynamic laws and is directly applicable to a wide class of nonequilibrium nanoscale systems.

2512.11613

Dec 2025Quantum Physics

Highly Nondegenerate Entangled Photon Source for Fiber-Based Quantum Key Distribution

Entangled photon sources (EPSs) are essential building blocks for scalable quantum communication and quantum key distribution (QKD). We present a stable, highly nondegenerate EPS based on type-0 spontaneous parametric down-conversion (SPDC) in a crossed-crystal configuration, generating photon pairs at 680~nm and 1550~nm when pumped by a 473~nm laser. This wavelength combination, reported here for the first time, simultaneously benefits from the peak detection efficiency of the most of the Si-SPADs in the visible/near-infrared spectral range and the low-loss fiber transmission of the telecom C-band. This configuration provides the most favorable balance between performance and cost for detection using Si-SPADs and InGaAs detectors. The source exhibits a measured spectral bandwidth of 300~GHz, corresponding to a spectral brightness of up to $1.9\times 10^3$~pairs~s$^{-1}$~mW$^{-1}$~GHz$^{-1}$. Heralding efficiencies reach 18~\% (signal) and 34~\% (idler) with Si-SPAD and superconducting nanowire single-photon detectors (SNSPD) detection. The entangled state achieves visibilities of $(97.3\pm 1.0)\,\%$ in the H/V basis and $(94.9\pm1.6)\,\%$ in the D/A basis, yielding a fidelity of $\geq(96.1\pm1.3)\,\%$. These results establish the presented EPS as a practical wavelength-hybrid platform for fiber-based QKD and emerging long-haul quantum network architectures.

2512.11630

Dec 2025Quantum Physics

Real-Time Polarization Control for Satellite QKD with Liquid-Crystal Beacon Stabilization

Polarization instability is a critical challenge for polarization-entangled satellite quantum key distribution (QKD), where atmospheric effects and platform motion continuously distort photon polarization. To maintain entanglement fidelity, these transformations must be precisely identified and compensated before detection. The channel-induced polarization rotation of a classical reference signal (beacon) is characterized using liquidcrystal variable retarders as a compact and fast polarizationcompensation approach, enabling real-time polarization tracking for satellite QKD links.

2512.11714

Dec 2025Quantum Physics

Bloch oscillation in a Floquet engineering quadratic potential system

We investigate the quantum dynamics of a one-dimensional tight-binding lattice driven by a spatially quadratic and time-periodic potential. Both Hermitian ($J_1 = J_2$) and non-Hermitian ($J_1 \neq J_2$) hopping regimes are analyzed. Within the framework of Floquet theory, the time-dependent Hamiltonian is mapped onto an effective static Floquet Hamiltonian, enabling a detailed study of the quasi-energy spectrum and eigenstate localization as function of the driving frequency $ω$. We identify critical frequencies $ω_c$ at which nearly equidistant quasi-energy ladders emerge, characterized by a pronounced minimum in the normalized variance of level spacings. This spectral regularity, which coincides with a peak in the mean inverse participation ratio (\textrm{MIPR}), leads to robust periodic revivals and Bloch-like oscillations in the time evolution. Numerical simulations confirm that such coherent oscillations persist even in the non-Hermitian regime, where the periodic driving stabilizes an almost real and uniformly spaced quasi-energy ladder.

2512.11675

Dec 2025Quantum Physics

A slightly improved upper bound for quantum statistical zero-knowledge

The complexity class Quantum Statistical Zero-Knowledge ($\mathsf{QSZK}$), introduced by Watrous (FOCS 2002) and later refined in Watrous (SICOMP, 2009), has the best known upper bound $\mathsf{QIP(2)} \cap \text{co-}\mathsf{QIP(2)}$, which was simplified following the inclusion $\mathsf{QIP(2)} \subseteq \mathsf{PSPACE}$ established in Jain, Upadhyay, and Watrous (FOCS 2009). Here, $\mathsf{QIP(2)}$ denotes the class of promise problems that admit two-message quantum interactive proof systems in which the honest prover is typically \textit{computationally unbounded}, and $\text{co-}\mathsf{QIP(2)}$ denotes the complement of $\mathsf{QIP(2)}$. We slightly improve this upper bound to $\mathsf{QIP(2)} \cap \text{co-}\mathsf{QIP(2)}$ with a quantum linear-space honest prover. A similar improvement also applies to the upper bound for the non-interactive variant $\mathsf{NIQSZK}$. Our main techniques are an algorithmic version of the Holevo-Helstrom measurement and the Uhlmann transform, both implementable in quantum linear space, implying polynomial-time complexity in the state dimension, using the recent space-efficient quantum singular value transformation of Le Gall, Liu, and Wang (CC, to appear).

2512.11597

Dec 2025Quantum Physics

An end-to-end quantum algorithm for nonlinear fluid dynamics with bounded quantum advantage

Computational fluid dynamics (CFD) is a cornerstone of classical scientific computing, and there is growing interest in whether quantum computers can accelerate such simulations. To date, the existing proposals for fault-tolerant quantum algorithms for CFD have almost exclusively been based on the Carleman embedding method, used to encode nonlinearities on a quantum computer. In this work, we begin by showing that these proposals suffer from a range of severe bottlenecks that negate conjectured quantum advantages: lack of convergence of the Carleman method, prohibitive time-stepping requirements, unfavorable condition number scaling, and inefficient data extraction. With these roadblocks clearly identified, we develop a novel algorithm for the incompressible lattice Boltzmann equation that circumvents these obstacles, and then provide a detailed analysis of our algorithm, including all potential sources of algorithmic complexity, as well as gate count estimates. We find that for an end-to-end problem, a modest quantum advantage may be preserved for selected observables in the high-error-tolerance regime. We lower bound the Reynolds number scaling of our quantum algorithm in dimension $D$ at Kolmogorov microscale resolution with $O(\mathrm{Re}^{\frac{3}{4}(1+\frac{D}{2})} \times q_M)$, where $q_M$ is a multiplicative overhead for data extraction with $q_M = O(\mathrm{Re}^{\frac{3}{8}})$ for the drag force. This upper bounds the scaling improvement over classical algorithms by $O(\mathrm{Re}^{\frac{3D}{8}})$. However, our numerical investigations suggest a lower speedup, with a scaling estimate of $O(\mathrm{Re}^{1.936} \times q_M)$ for $D=2$. Our results give robust evidence that small, but nontrivial, quantum advantages can be achieved in the context of CFD, and motivate the need for additional rigorous end-to-end quantum algorithm development.

2512.037581

Dec 2025Quantum Physics

Fault-tolerant quantum computation with constant overhead for general noise

Fault-tolerant quantum computation traditionally incurs substantial resource overhead, with both qubit and time overheads scaling polylogarithmically with the size of the computation. While prior work by Gottesman showed that constant qubit overhead is achievable under stochastic noise using quantum low-density parity-check (QLDPC) codes, it has remained an open question whether similar guarantees hold under more general, non-stochastic noise models. In this work, we address this question by considering a general circuit-level noise model defined via the diamond norm, which captures both stochastic and non-stochastic noise, including coherent and amplitude damping noise. We prove that constant qubit overhead fault-tolerant quantum computation is achievable in this general setting, using QLDPC codes with constant rate and linear minimum distance. To establish our result, we develop a fault-tolerant error correction scheme and a method for implementing logic gates under general circuit noise. These results extend the theoretical foundations of fault-tolerant quantum computation and offer new directions for fault-tolerant architectures under realistic noise models.

2512.02760

Dec 2025Quantum Physics

A Heptalemma for Quantum Mechanics

We present a seven-pronged no-go result for quantum mechanics: a "heptalemma". It shows that seven initially plausible theses about physical reality are jointly inconsistent with the predictions of quantum mechanics, while any six are jointly consistent. We must then decide which theses to retain and which to give up. Since different interpretations of quantum mechanics entail different responses to the heptalemma, we get a novel taxonomy of such interpretations. Beyond the application to quantum mechanics, the heptalemma offers a general diagnostic criterion for determining whether a given scientific domain should count as classical or not, and if not, how it departs from classicality.

2512.01982

Dec 2025Quantum Physics

4,872 papers

Improved Lower Bounds for Learning Quantum Channels in Diamond Distance

We prove that learning an unknown quantum channel with input dimension $d_A$, output dimension $d_B$, and Choi rank $r$ to diamond distance $\varepsilon$ requires $ Ω\!\left( \frac{d_A d_B r}{\varepsilon \log(d_B r / \varepsilon)} \right)$ queries. This improves the best previous $Ω(d_A d_B r)$ bound by introducing explicit $\varepsilon$-dependence, with a scaling in $\varepsilon$ that is near-optimal when $d_A=rd_B$ but not tight in general. The proof constructs an ensemble of channels that are well-separated in diamond norm yet admit Stinespring isometries that are close in operator norm.

2601.04180Jan 2026

View

Below-shot-noise capacity in phase estimation using nonlinear interferometers

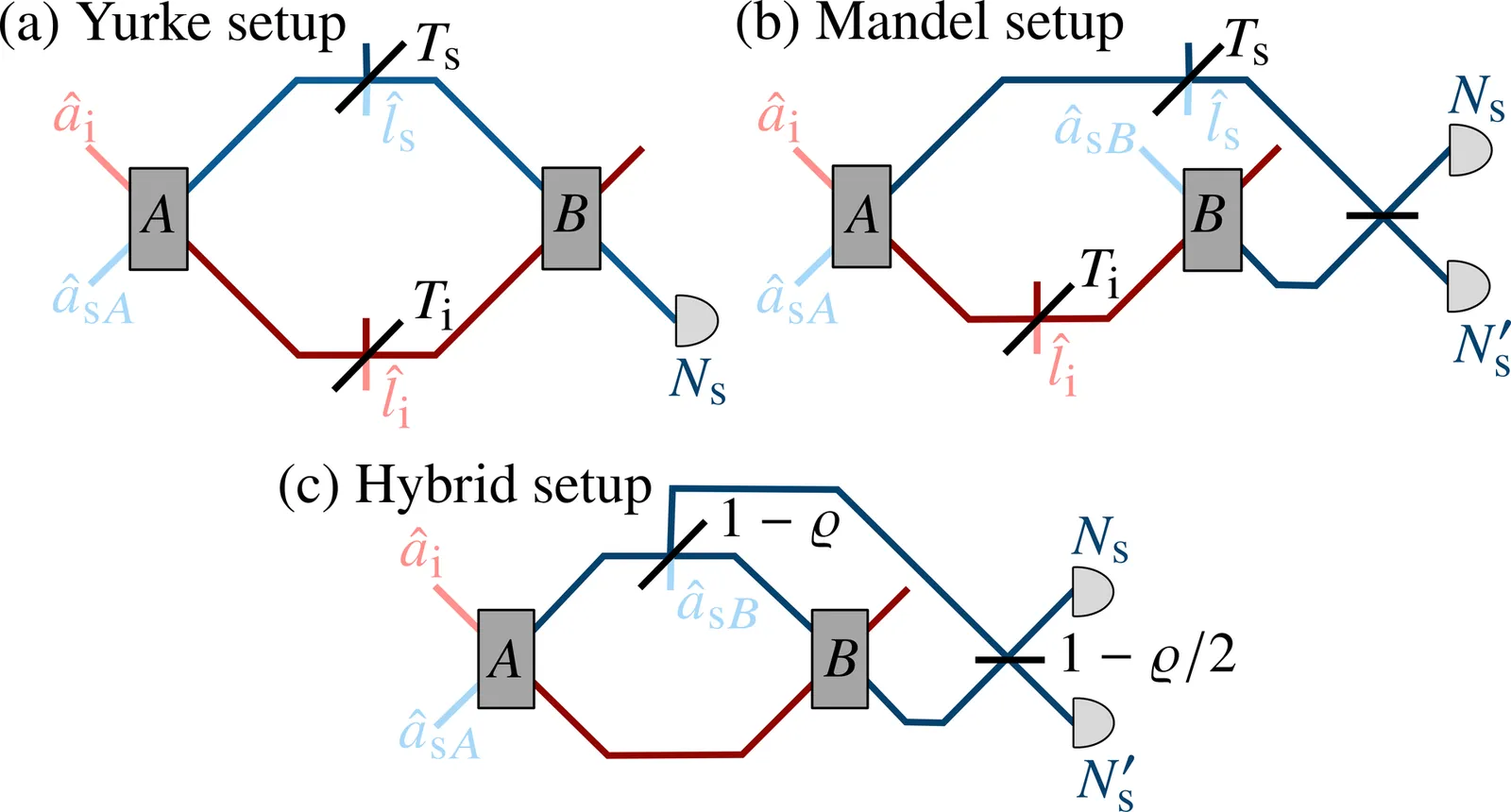
Over the past decade, several schemes for imaging and sensing based on nonlinear interferometers have been proposed and demonstrated experimentally. These interferometers exhibit two main advantages. First, they enable probing a sample at a chosen wavelength while detecting light at a different wavelength with high efficiency (bicolor quantum imaging and sensing with undetected light). Second, they can show quantum-enhanced sensitivities below the shot-noise limit, potentially reaching Heisenberg-limited precision in parameter estimation. Here, we compare three quantum-imaging configurations using only easily accessible intensity-based measurements for phase estimation: a Yurke-type SU(1,1) interferometer, a Mandel-type induced-coherence interferometer, and a hybrid scheme that continuously interpolates between them. While an ideal Yurke interferometer can exhibit Heisenberg scaling, this advantage is known to be fragile under realistic detection constraints and in the presence of loss. We demonstrate that differential intensity detection in the Mandel interferometer provides the highest and most robust phase sensitivity among the considered schemes, reaching but not surpassing the shot-noise limit, even in the presence of loss. Intensity measurements in a Yurke-type configuration can achieve genuine sub-shot-noise sensitivity under balanced losses and moderate gain; however, their performance degrades in realistic high-gain regimes. Consequently, in this regime, the Mandel configuration with differential detection outperforms the Yurke-type setup and constitutes the most robust approach for phase estimation.

2601.04139Jan 2026

View

Extracting scattering phase shift in quantum mechanics on quantum computers

We investigate the feasibility of extracting infinite volume scattering phase shift on quantum computers in a simple one-dimensional quantum mechanical model, using the formalism established in Ref.~\cite{Guo:2023ecc} that relates the integrated correlation functions (ICF) for a trapped system to the infinite volume scattering phase shifts through a weighted integral. The system is first discretized in a finite box with periodic boundary conditions, and the formalism in real time is verified by employing a contact interaction potential with exact solutions. Quantum circuits are then designed and constructed to implement the formalism on current quantum computing architectures. To overcome the fast oscillatory behavior of the integrated correlation functions in real-time simulation, different methods of post-data analysis are proposed and discussed. Test results on IBM hardware show that good agreement can be achieved with two qubits, but complete failure ensues with three qubits due to two-qubit gate operation errors and thermal relaxation errors.

2601.04092Jan 2026

View

Surface Optimization of Aluminum Resonators for Robust Quantum Device Fabrication

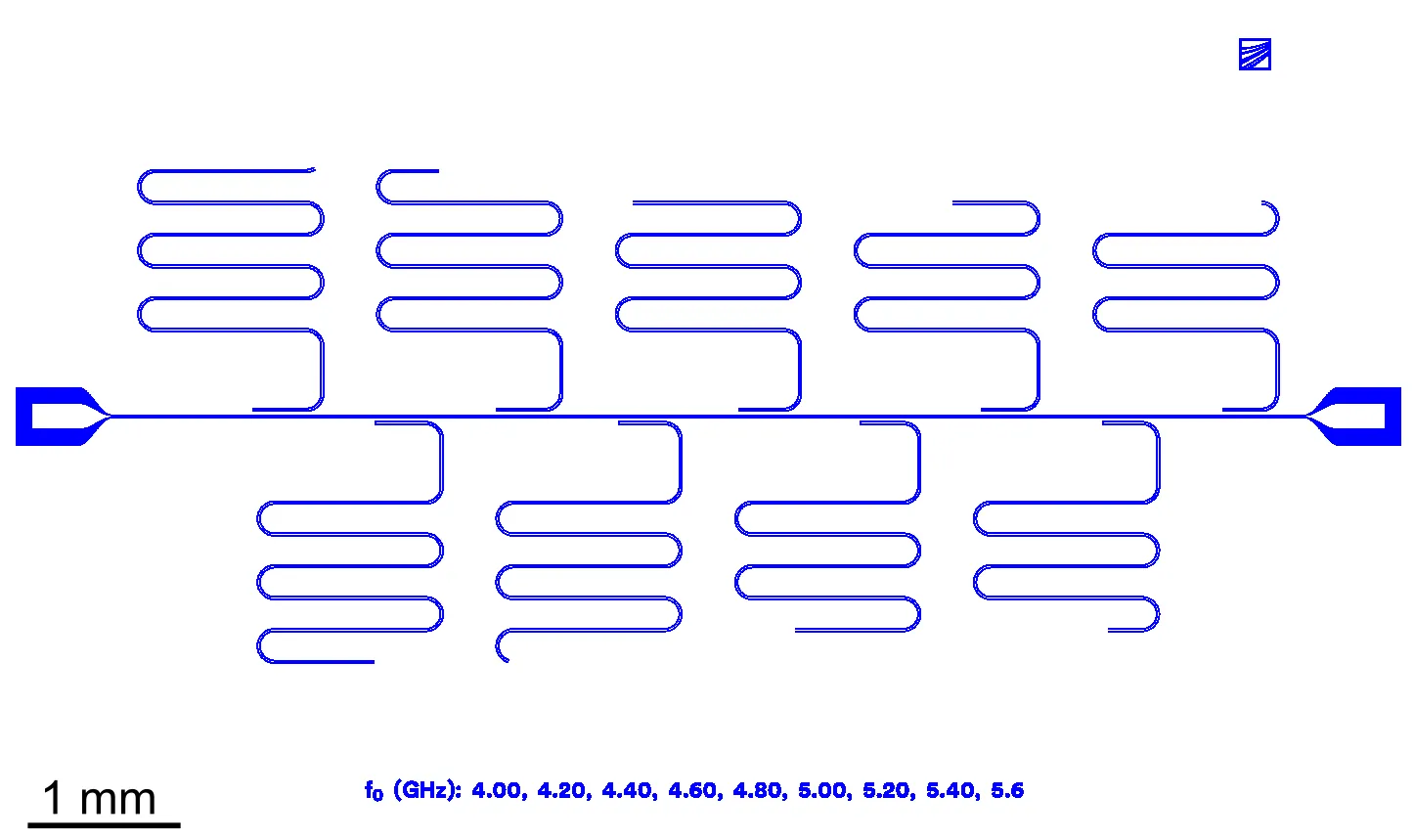
Aluminum remains the central material for superconducting qubits, and considerable effort has been devoted to optimizing its deposition and patterning for quantum devices. However, while post-processing of Nb- and Ta-based resonators has been widely explored, primarily focusing on oxide removal using buffered oxide etch (BOE), post-treatment strategies for Al resonators remain underdeveloped. This challenge becomes particularly relevant for industry-scale fabrication with multichip bonding, where delays between sample preparation and cooldown require surface treatments that preserve low dielectric loss during extended exposure to ambient conditions. In this work, we investigate surface modification approaches for Al resonators subjected to a 24-hour delay prior to cryogenic measurement. Passivation using self-limiting oxygen and fluorine chemistries was evaluated utilizing different plasma processes. Remote oxygen plasma treatment reduced dielectric losses, in contrast to direct plasma, likely due to additional ashing of residual resist despite the formation of a thicker oxide layer on both Si and Al surfaces. A fluorine-based plasma process was developed that passivated the Al surface with fluorine for subsequent BOE treatment. However, increasing fluorine incorporation in the aluminum oxide correlated with higher loss, identifying fluorine as an unsuitable passivation material for Al resonators. Finally, selective oxide removal using HF vapor and phosphoric acid was assessed for surface preparation. HF vapor selectively etched SiO2 while preserving Al2O3, whereas phosphoric acid exhibited the opposite selectivity. Sequential application of both etches yielded dielectric losses as low as $δ_\mathrm{LP} = 5.2 \times 10^{-7}$ ($Q\mathrm{i} \approx 1.9\,\mathrm{M}$) in the single photon regime, demonstrating a promising pathway for robust Al-based resonator fabrication.

2601.04082Jan 2026

View

Phase-Randomized Laser Pulse Generation at 10 GHz for Quantum Photonic Applications

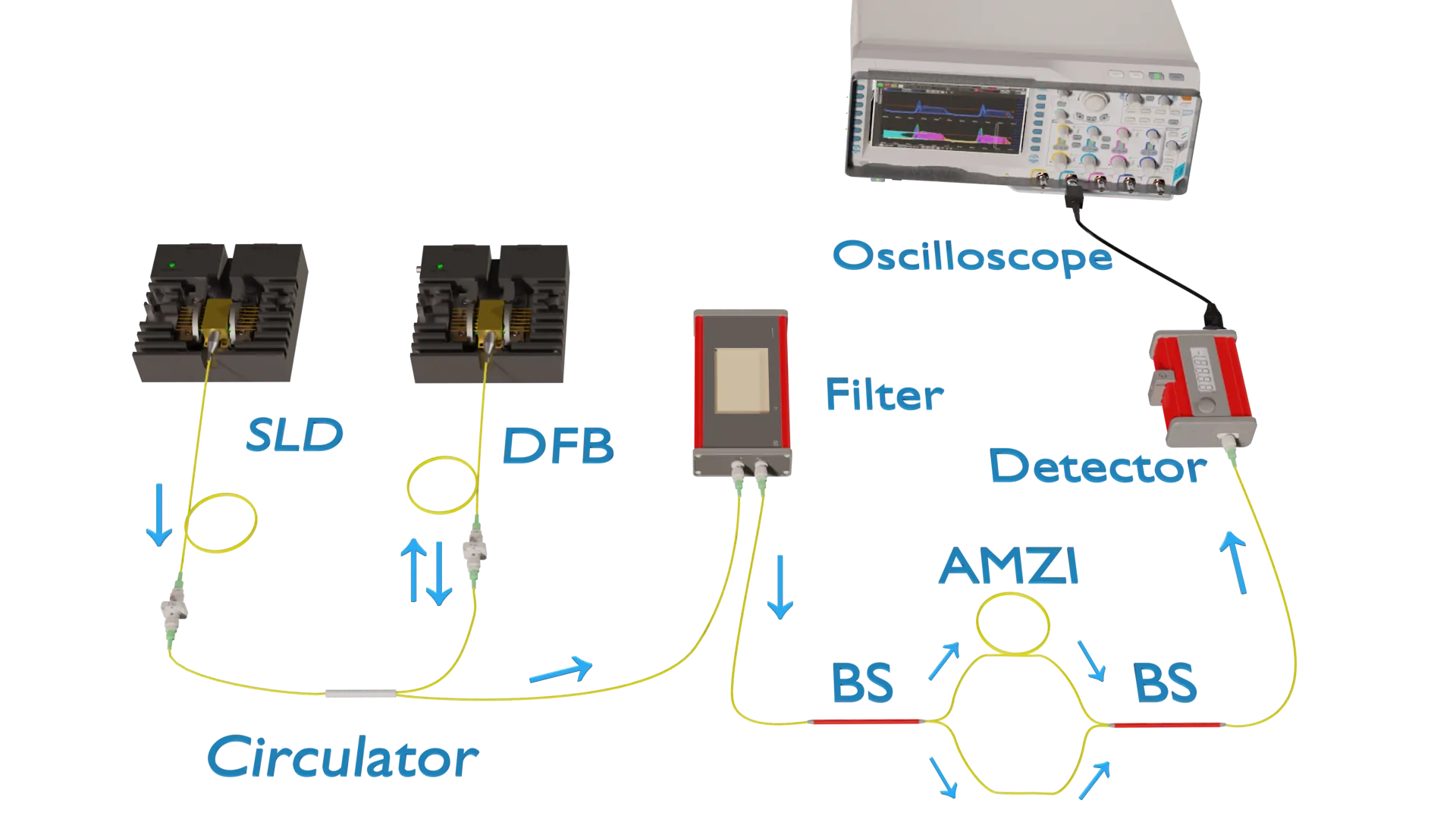
Gain-switching laser diodes is a well-established technique for generating optical pulses with random phases, where the quantum randomness arises naturally from spontaneous emission. However, the maximum switching rate is limited by phase diffusion: at high repetition rates, residual photons in the cavity seed subsequent pulses, leading to phase correlations, which degrade randomness. We present a method to overcome this limitation by employing an external source of spontaneous emission in conjunction with the laser. Our results show that this approach effectively removes interpulse phase correlations and restores phase randomization at repetition rates as high as 10 GHz. This technique opens new opportunities for high-rate quantum key distribution and quantum random number generation.

2601.04031Jan 2026

View

Limitations for adaptive quantum state tomography in the presence of detector noise

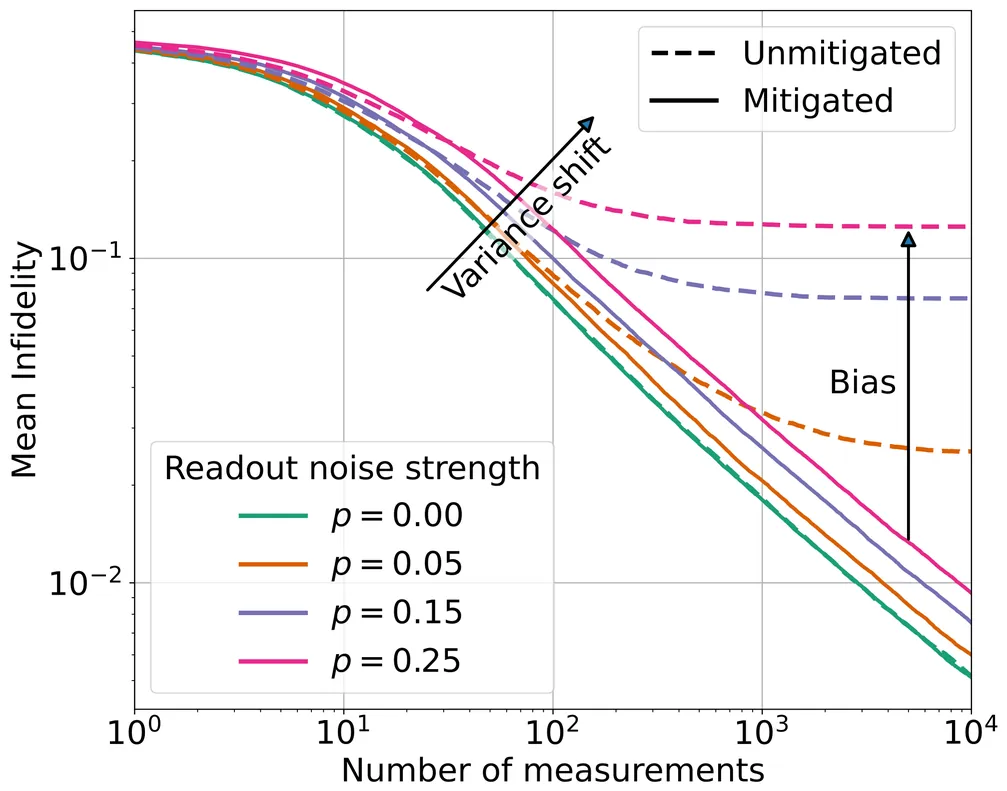
Assumption-free reconstruction of quantum states from measurements is essential for benchmarking and certifying quantum devices, but it remains difficult due to the extensive measurement statistics and experimental resources it demands. An approach to alleviating these demands is provided by adaptive measurement strategies, which can yield up to a quadratic improvement in reconstruction accuracy for pure states by dynamically optimizing measurement settings during data acquisition. A key open question is whether these asymptotic advantages remain in realistic experiments, where readout is inevitably noisy. In this work, we analyze the impact of readout noise on adaptive quantum state tomography with readout-error mitigation, focusing on the challenging regime of reconstructing pure states using mixed-state estimators. Using analytical arguments based on Fisher information optimization and extensive numerical simulations using Bayesian inference, we show that any nonzero readout noise eliminates the asymptotic quadratic scaling advantage of adaptive strategies. We numerically investigate the behavior for finite measurement statistics for single- and two-qubit systems with exact readout-error mitigation and find a gradual transition from ideal to sub-optimal scaling. We furthermore investigate realistic scenarios where detector tomography is performed with a limited number of state copies for calibration, showing that insufficient detector characterization leads to estimator bias and limited reconstruction accuracy. Although our result imposes an upper bound on the reconstruction accuracy that can be achieved with adaptive strategies, we nevertheless observe numerically a constant-factor gain in reconstruction accuracy, which becomes larger as the readout noise decreases. This indicates potential practical benefits in using adaptive measurement strategies in well-calibrated experiments.

2601.04020Jan 2026

View

Cavity-Driven Multispectral Gain for High-Sensitivity NV Center Magnetometers

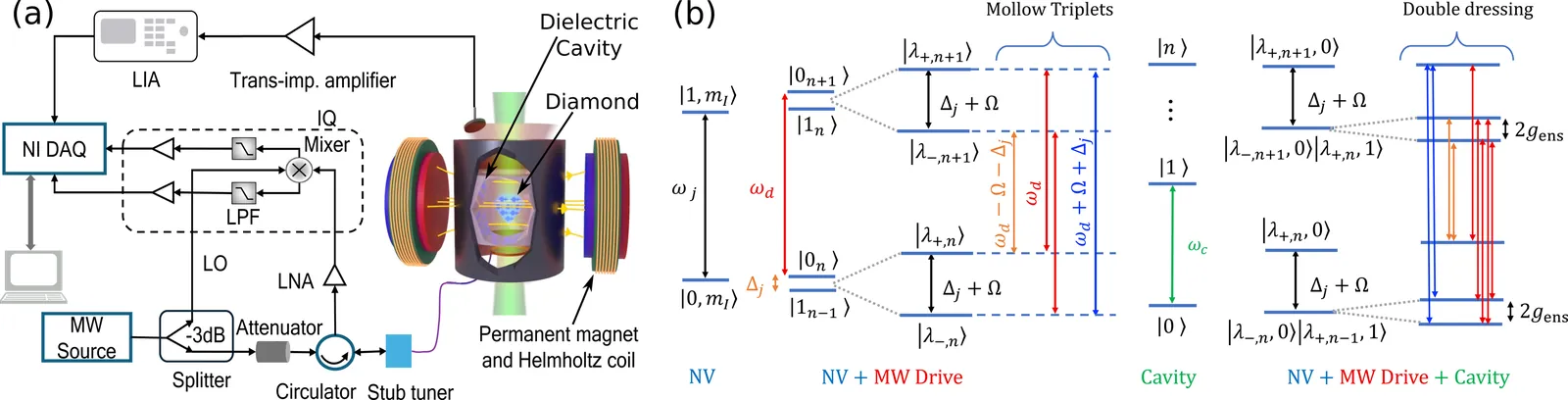
We report a cavity-enabled solid-state magnetometer based on an NV ensemble coupled with a dielectric cavity, achieving 12 pT/$\sqrt{\rm{Hz}}$ sensitivity and a nearly threefold gain from multispectral features. The features originate from cavity-induced splitting of the NV hyperfine levels and leverages robust quantum coherence in the doubly dressed states of the system to achieve high sensitivity. We project simulated near-term sensitivities approaching 100 fT/$\sqrt{\rm{Hz}}$, close to the Johnson-Nyquist limit. Our results establish frequency multiplexing as a new operational paradigm, offering a robust and scalable quantum resource for metrology under ambient conditions.

2601.03975Jan 2026

View

Integration and Resource Estimation of Cryoelectronics for Superconducting Fault-Tolerant Quantum Computers

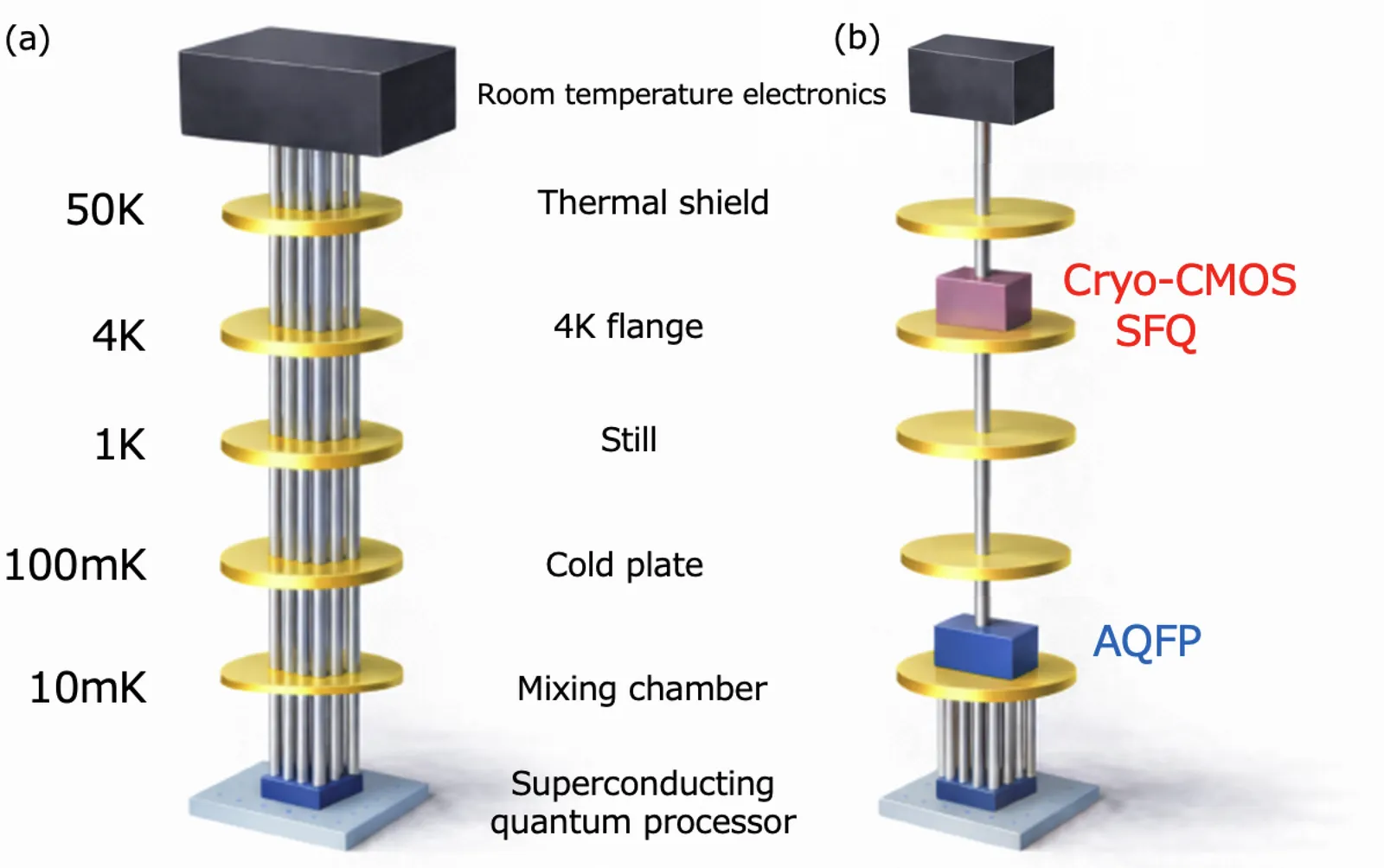
Scaling superconducting quantum computers to the fault-tolerant regime calls for a commensurate scaling of the classical control and readout stack. Today's systems largely rely on room-temperature, rack-based instrumentation connected to dilution-refrigerator cryostats through many coaxial cables. Looking ahead, superconducting fault-tolerant quantum computers (FTQCs) will likely adopt a heterogeneous quantum-classical architecture that places selected electronics at cryogenic stages -- for example, cryo-CMOS at 4~K and superconducting digital logic at 4~K and/or mK stages -- to curb wiring and thermal-load overheads. This review distills key requirements, surveys representative room-temperature and cryogenic approaches, and provides a transparent first-order accounting framework for cryoelectronics. Using an RSA-2048-scale benchmark as a concrete reference point, we illustrate how scaling targets motivate constraints on multiplexing and stage-wise cryogenic power, and discuss implications for functional partitioning across room-temperature electronics, cryo-CMOS, and superconducting logic.

2601.03922Jan 2026

View

MPM-QIR: Measurement-Probability Matching for Quantum Image Representation and Compression via Variational Quantum Circuit

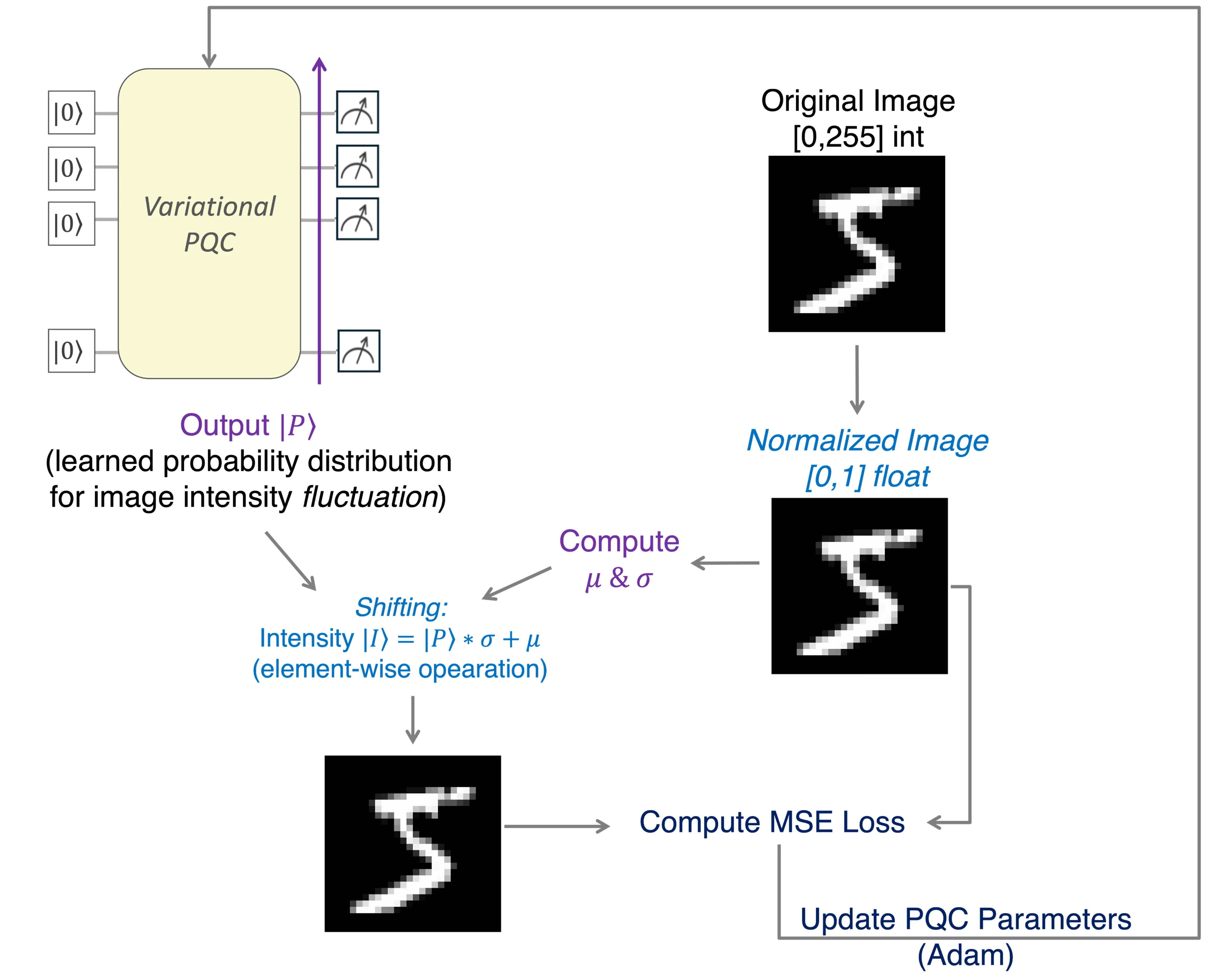
We present MPM-QIR, a variational-quantum-circuit (VQC) framework for classical image compression and representation whose core objective is to achieve equal or better reconstruction quality at a lower Parameter Compression Ratio (PCR). The method aligns a generative VQC's measurement-probability distribution with normalized pixel intensities and learns positional information implicitly via an ordered mapping to the flattened pixel array, thus eliminating explicit coordinate qubits and tying compression efficiency directly to circuit (ansatz) complexity. A bidirectional convolutional architecture induces long-range entanglement at shallow depth, capturing global image correlations with fewer parameters. Under a unified protocol, the approach attains PSNR $\geq$ 30 dB with lower PCR across benchmarks: MNIST 31.80 dB / SSIM 0.81 at PCR 0.69, Fashion-MNIST 31.30 dB / 0.91 at PCR 0.83, and CIFAR-10 31.56 dB / 0.97 at PCR 0.84. Overall, this compression-first design improves parameter efficiency, validates VQCs as direct and effective generative models for classical image compression, and is amenable to two-stage pipelines with classical codecs and to extensions beyond 2D imagery.

2601.03855Jan 2026

View

Iterative Matrix Product State Simulation for Scalable Grover's Algorithm

Grover's algorithm is a cornerstone of quantum search algorithm, offering quadratic speedup for unstructured problems. However, limited qubit counts and noise in today's noisy intermediate-scale quantum (NISQ) devices hinder large-scale hardware validation, making efficient classical simulation essential for algorithm development and hardware assessment. We present an iterative Grover simulation framework based on matrix product states (MPS) to efficiently simulate large-scale Grover's algorithm. Within the NVIDIA CUDA-Q environment, we compare iterative and common (non-iterative) Grover's circuits across statevector and MPS backends. On the MPS backend at 29 qubits, the iterative Grover's circuit runs about 15x faster than the common (non-iterative) Grover's circuit, and about 3-4x faster than the statevector backend. In sampling experiments, Grover's circuits demonstrate strong low-shot stability: as the qubit number increases beyond 13, a single-shot measurement still closely mirrors the results from 4,096 shots, indicating reliable estimates with minimal sampling and significant potential to cut measurement costs. Overall, an iterative MPS design delivers speed and scalability for Grover's circuit simulation, enabling practical large-scale implementations.

2601.03832Jan 2026

View

Finite-size security of QKD: comparison of three proof techniques

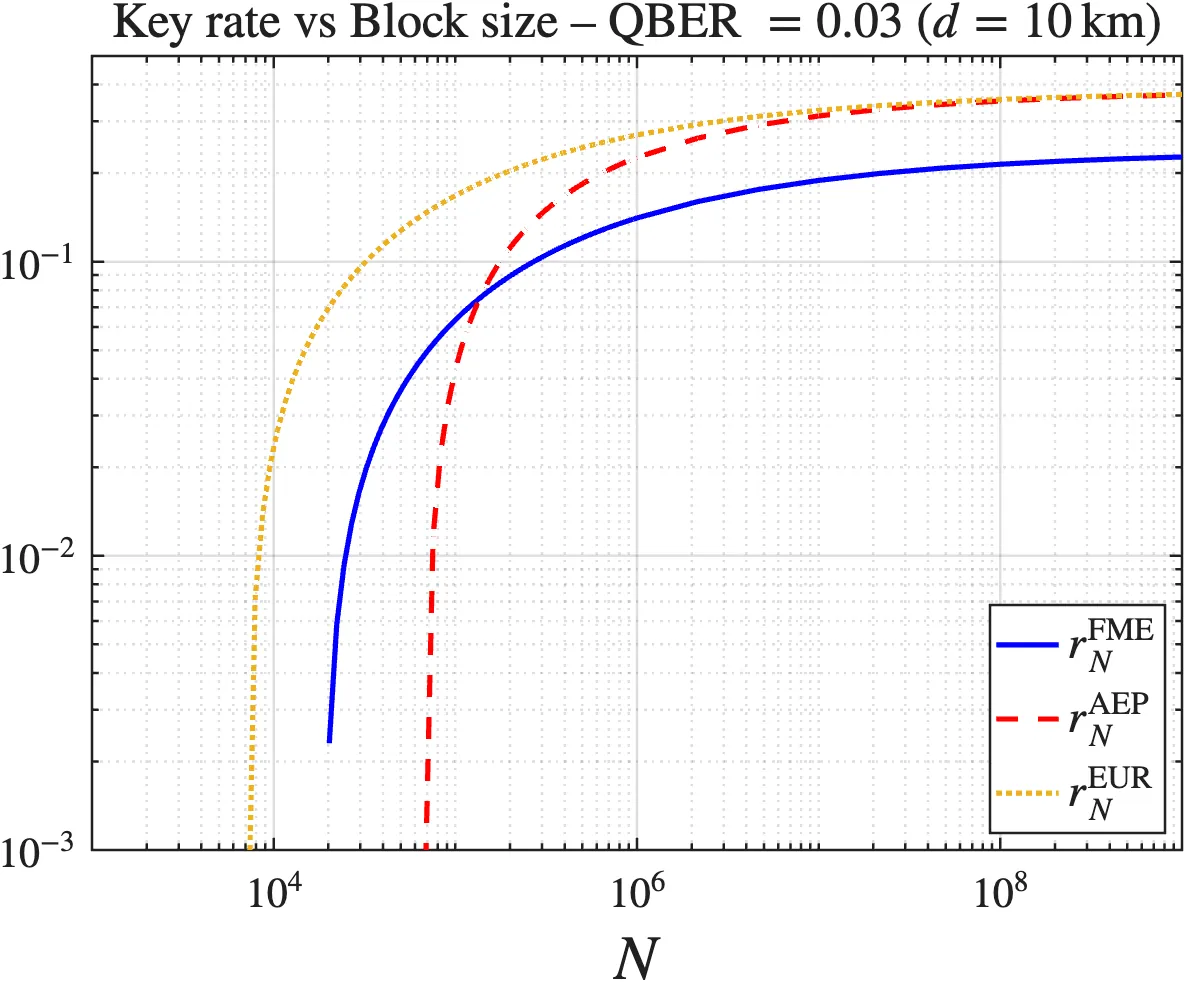
We compare three proof techniques for composable finite-size security of quantum key distribution under collective attacks, with emphasis on how the resulting secret-key rates behave at practically relevant block lengths. As a benchmark, we consider the BB84 protocol and evaluate finite-size key-rate estimates obtained from entropic uncertainty relations (EUR), from the asymptotic equipartition property (AEP), and from a direct finite-block analysis based on the conditional min-entropy, which we refer to as the finite-size min-entropy (FME) approach. For BB84 we show that the EUR-based bound provides the most favorable performance across the considered parameter range, while the AEP bound is asymptotically tight but can become overly pessimistic at moderate and small block sizes, where it may fail to certify a positive key. The FME approach remains effective in this small-block regime, yielding nonzero rates in situations where the AEP estimate vanishes, although it is not asymptotically optimal for BB84. These results motivate the use of FME-type analyses for continuous-variable protocols in settings where tight EUR-based bounds are unavailable, notably for coherent-state schemes where current finite-size analyses typically rely on AEP-style corrections.

2601.03829Jan 2026

View

Topological Sensing in the Dynamics of Quantum Walks with Defects

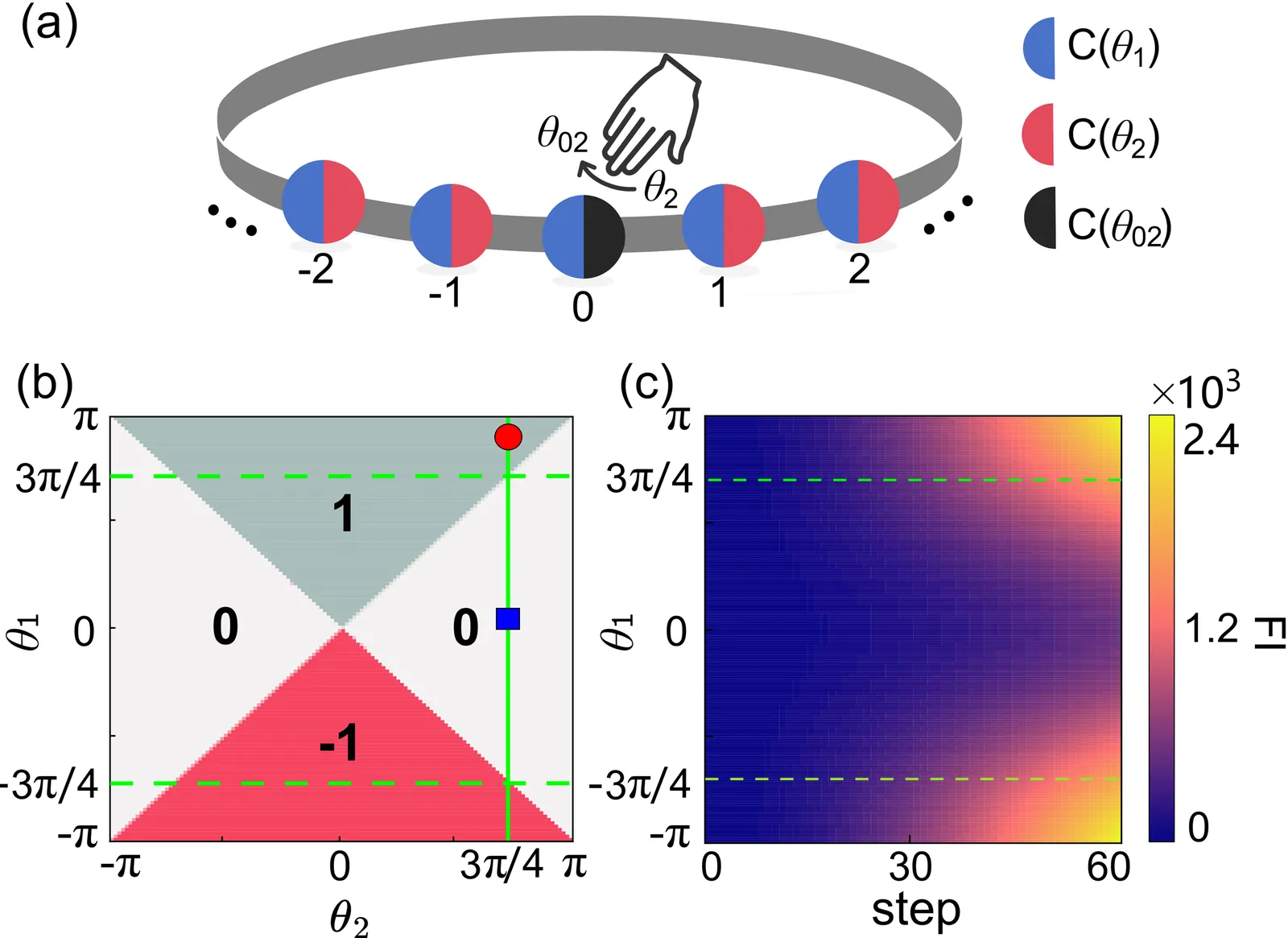
Topological quantum sensing leverages unique topological features to suppress noise and improve the precision of parameter estimation, emerging as a promising tool in both fundamental research and practical application. In this Letter, we propose a sensing protocol that exploits the dynamics of topological quantum walks incorporating localized defects. Unlike conventional schemes that rely on topological protection to suppress disorder and defects, our protocol harnesses the evolution time as a resource to enable precise estimation of the defect parameter. By utilizing topologically nontrivial properties of the quantum walks, the sensing precision can approach the Heisenberg limit. We further demonstrate the performance and robustness of the protocol through Bayesian estimation. Our results show that this approach maintains high precision over a broad range of parameters and exhibits strong robustness against disorder, offering a practical pathway for topologically enhanced quantum metrology.

2601.03821Jan 2026

View

Detection-loophole-free nonlocality in the simplest scenario

Loophole-free quantum nonlocality often demands experiments with high complexity (defined by all parties' settings and outcomes) and multiple efficient detectors. Here, we identify the fundamental efficiency and complexity thresholds for quantum steering using two-qubit entangled states. Remarkably, it requires only one photon detector on the untrusted side, with efficiency $ε> 1/X$, where $X \geq 2$ is the number of settings on that side. This threshold applies to all pure entangled states, in contrast to analogous Bell-nonlocality tests, which require almost unentangled states to be loss-tolerant. We confirm these predictions in a minimal-complexity ($X = 2$ for the untrusted party and a single three-outcome measurement for the trusted party), detection-loophole-free photonic experiment with $ε= (51.6 \pm 0.4)\% $.

2601.03817Jan 2026

View

2601.03734

Computational hardness of estimating quantum entropies via binary entropy bounds

We investigate the computational hardness of estimating the quantum $α$-Rényi entropy ${\rm S}^{\tt R}_α(ρ) = \frac{\ln {\rm Tr}(ρ^α)}{1-α}$ and the quantum $q$-Tsallis entropy ${\rm S}^{\tt T}_q(ρ) = \frac{1-{\rm Tr}(ρ^q)}{q-1}$, both converging to the von Neumann entropy as the order approaches $1$. The promise problems Quantum $α$-Rényi Entropy Approximation (RényiQEA$_α$) and Quantum $q$-Tsallis Entropy Approximation (TsallisQEA$_q$) ask whether $ {\rm S}^ {\tt R}_α(ρ)$ or ${\rm S}^{\tt T}_q(ρ)$, respectively, is at least $τ_{\tt Y}$ or at most $τ_{\tt N}$, where $τ_{\tt Y} - τ_{\tt N}$ is typically a positive constant. Previous hardness results cover only the von Neumann entropy (order $1$) and some cases of the quantum $q$-Tsallis entropy, while existing approaches do not readily extend to other orders. We establish that for all positive real orders, the rank-$2$ variants Rank2RényiQEA$_α$ and Rank2TsallisQEA$_q$ are ${\sf BQP}$-hard. Combined with prior (rank-dependent) quantum query algorithms in Wang, Guan, Liu, Zhang, and Ying (TIT 2024), Wang, Zhang, and Li (TIT 2024), and Liu and Wang (SODA 2025), our results imply: - For all real orders $α> 0$ and $0 < q \leq 1$, LowRankRényiQEA$_α$ and LowRankTsallisQEA$_q$ are ${\sf BQP}$-complete, where both are restricted versions of RényiQEA$_α$ and TsallisQEA$_q$ with $ρ$ of polynomial rank. - For all real order $q>1$, TsallisQEA$_q$ is ${\sf BQP}$-complete. Our hardness results stem from reductions based on new inequalities relating the $α$-Rényi or $q$-Tsallis binary entropies of different orders, where the reductions differ substantially from previous approaches, and the inequalities are also of independent interest.

2601.03734Jan 2026

View

Double interval entanglement in quasiparticle excited states

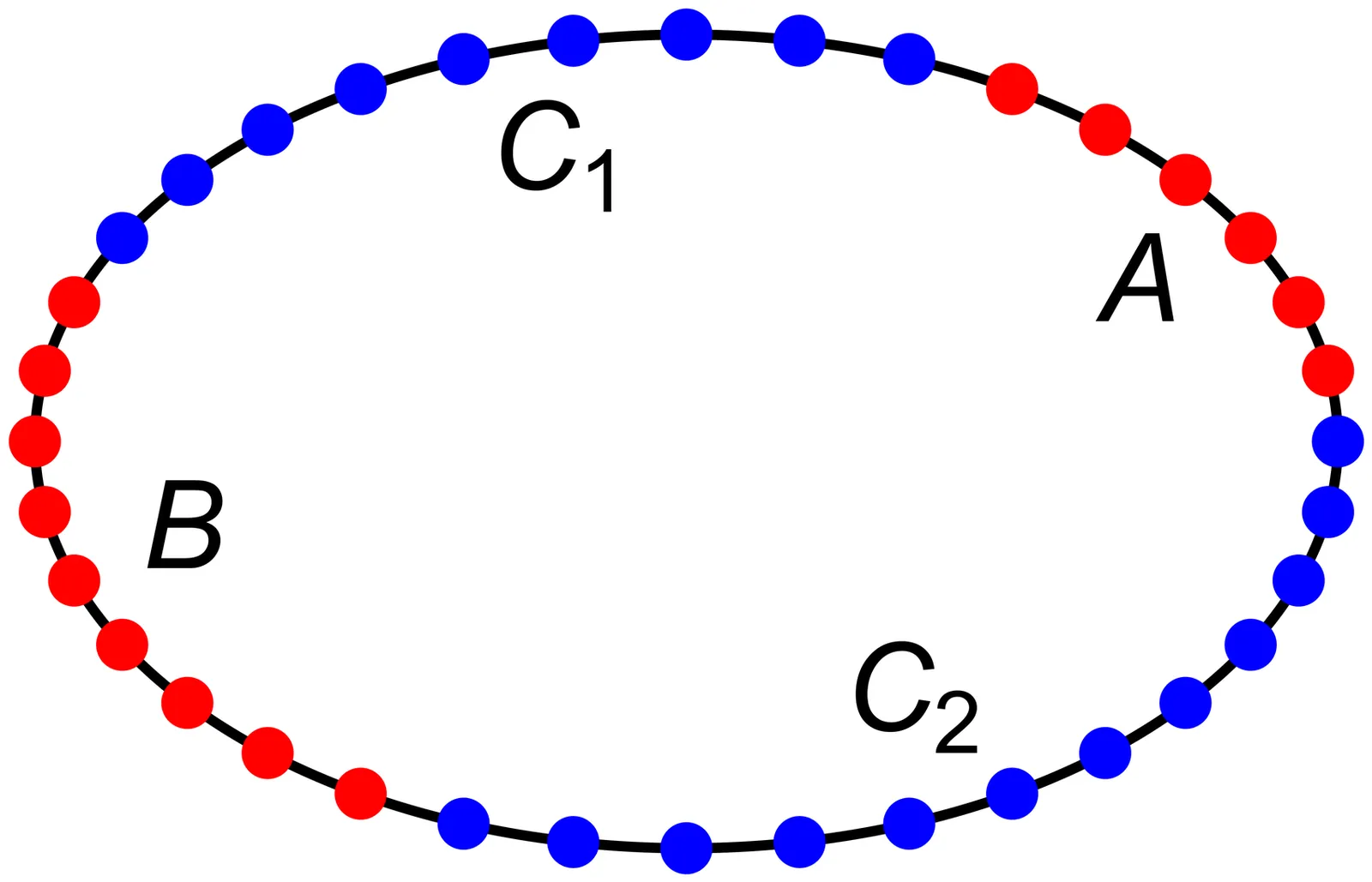
We investigate double-interval entanglement measures, specifically reflected entropy, mutual information, and logarithmic negativity, in quasiparticle excited states for classical, bosonic, and fermionic systems. We develop an algorithm that efficiently calculates these measures from density matrices expressed in a non-orthonormal basis, enabling straightforward numerical implementation. We find a universal additivity property that emerges at large momentum differences, where the entanglement measures for states with distinct quasiparticle sets equal the sum of their individual contributions. The classical limit arises as a special case of this additivity, with both bosonic and fermionic results converging to classical behavior when all momentum differences are large.

2601.03651Jan 2026

View

Strip-Symmetric Quantum Codes for Biased Noise: Z-Decoupling in Stabilizer and Floquet Codes

Bias-tailored codes such as the XZZX surface code and the domain wall color code achieve high dephasing-biased thresholds because, in the infinite-bias limit, their $Z$ syndromes decouple into one-dimensional repetition-like chains; the $X^3Z^3$ Floquet code shows an analogous strip-wise structure for detector events in spacetime. We capture this common mechanism by defining strip-symmetric biased codes, a class of static stabilizer and dynamical (Floquet) codes for which, under pure dephasing and perfect measurements, each elementary $Z$ fault is confined to a strip and the Z-detector--fault incidence matrix is block diagonal. For such codes the Z-detector hypergraph decomposes into independent strip components and maximum-likelihood $Z$ decoding factorizes across strips, yielding complexity savings for matching-based decoders. We characterize strip symmetry via per-strip stabilizer products, viewed as a $\mathbb{Z}_2$ 1-form symmetry, place XZZX, the domain wall color code, and $X^3Z^3$ in this framework, and introduce synthetic strip-symmetric detector models and domain-wise Clifford constructions that serve as design tools for new bias-tailored Floquet codes.

2601.03623Jan 2026

View

Transmutation based Quantum Simulation for Non-unitary Dynamics

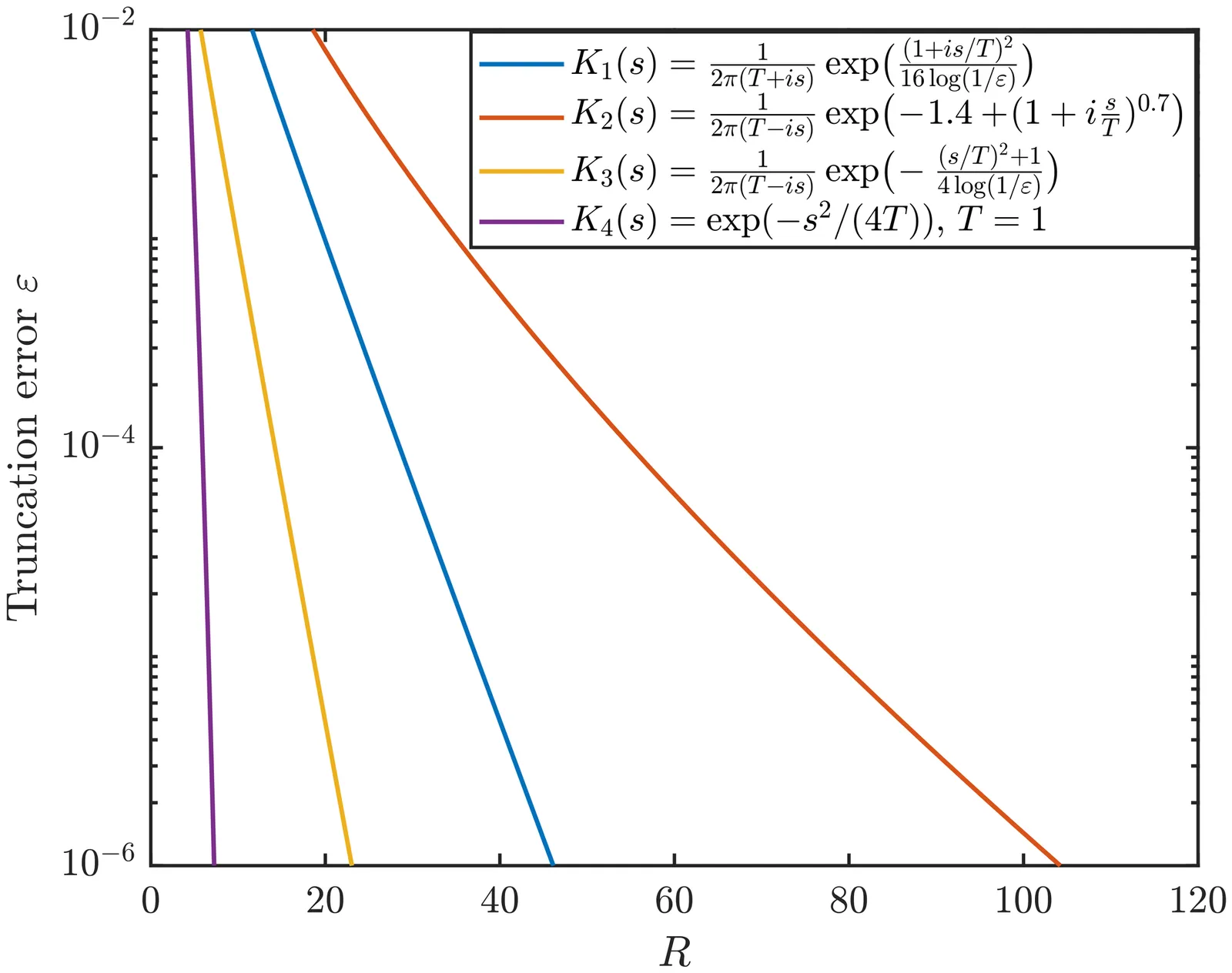
We present a quantum algorithm for simulating dissipative diffusion dynamics generated by positive semidefinite operators of the form $A=L^\dagger L$, a structure that arises naturally in standard discretizations of elliptic operators. Our main tool is the Kannai transform, which represents the diffusion semigroup $e^{-TA}$ as a Gaussian-weighted superposition of unitary wave propagators. This representation leads to a linear-combination-of-unitaries implementation with a Gaussian tail and yields query complexity $\tilde{\mathcal{O}}(\sqrt{\|A\| T \log(1/\varepsilon)})$, up to standard dependence on state-preparation and output norms, improving the scaling in $\|A\|, T$ and $\varepsilon$ compared with generic Hamiltonian-simulation-based methods. We instantiate the method for the heat equation and biharmonic diffusion under non-periodic physical boundary conditions, and we further use it as a subroutine for constant-coefficient linear parabolic surrogates arising in entropy-penalization schemes for viscous Hamilton--Jacobi equations. In the long-time regime, the same framework yields a structured quantum linear solver for $A\mathbf{x}=\mathbf{b}$ with $A=L^\dagger L$, achieving $\tilde{\mathcal{O}}(κ^{3/2}\log^2(1/\varepsilon))$ queries and improving the condition-number dependence over standard quantum linear-system algorithms in this factorized setting.

2601.03616Jan 2026

View

Local Scale Invariance in Quantum Theory: A Non-Hermitian Pilot-Wave Formulation

We show that Weyl's abandoned idea of local scale invariance has a natural realization at the quantum level in pilot-wave (deBroglie-Bohm) theory. We obtain the Weyl covariant derivative by complexifying the electromagnetic gauge coupling parameter. The resultant non-hermiticity has a natural interpretation in terms of local scale invariance of the quantum state in pilot-wave theory. The conserved current density is modified from $|ψ|^2$ to the local scale invariant, trajectory-dependent ratio $|ψ|^2/ \mathbf{1}^2[\mathcal{C}]$, where $\mathbf 1[\mathcal C]$ is a scale factor that depends on the pilot-wave trajectory $\mathcal C$ in configuration space. Our approach is general, and we implement it for the Schrödinger, Pauli, and Dirac equations coupled to an external electromagnetic field. We also implement it in quantum field theory for the case of a quantized axion field interacting with a quantized electromagnetic field. We discuss the equilibrium probability density and show that the corresponding trajectories are unique.

2601.03567Jan 2026

View

Tailoring Dynamical Quantum Phase Transitions via Double-Mode Squeezing Manipulation

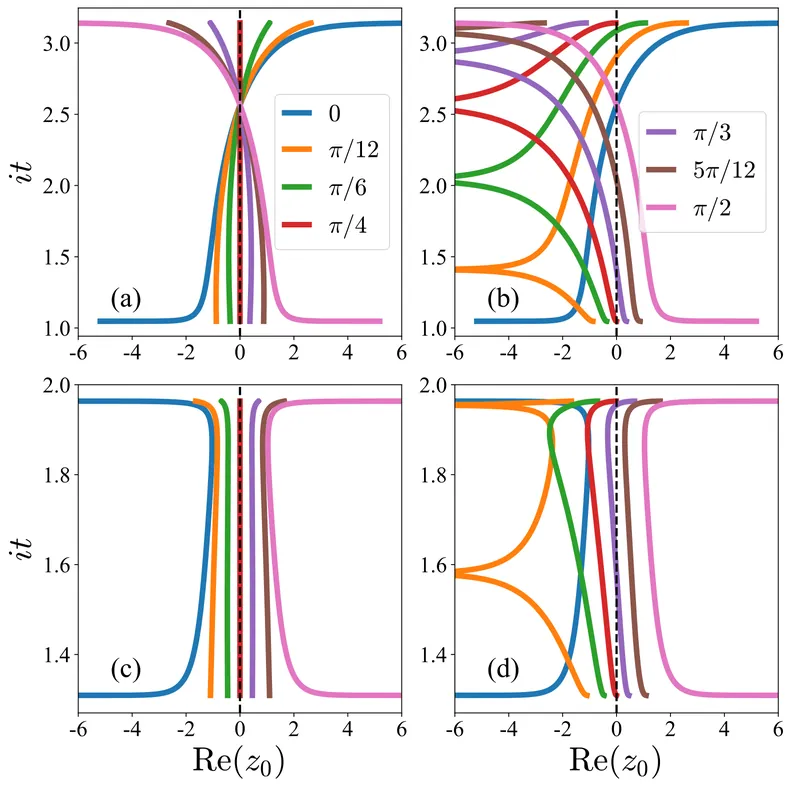
We propose a protocol to tailor dynamical quantum phase transitions (DQPTs) by double-mode squeezing onto the initial state in the XY chain. The effect of squeezing depends critically on the system's symmetry and parameters. When the squeezing operator breaks particle-hole symmetry (PHS), DQPTs become highly tunable, allowing one to either induce transitions within a single phase or suppress them. Remarkably, when PHS is preserved and the squeezing strength reaches $r=π/4$, a universal class of DQPTs emerges, independent of the quench path. This universality is characterized by two key features: (i) the collapse of all Fisher zeros onto the real-time axis, and (ii) the saturation of intermode entanglement to its maximum in each $(k,-k)$ modes. Moreover, the critical momenta governing the DQPTs coincide exactly with the modes attaining the maximal entanglement. At this universal point, the dynamical phase vanishes, leading to a purely geometric evolution marked by $π$-jumps in the Pancharatnam geometric phase. Our work establishes initial-state squeezing as a versatile tool for tailoring far-from-equilibrium criticality and reveals a direct link between entanglement saturation and universal nonanalytic dynamics.

2601.03494Jan 2026

View

Many-body Quantum Score: a scalable benchmark for digital and analog quantum processors and first test on a commercial neutral atom device

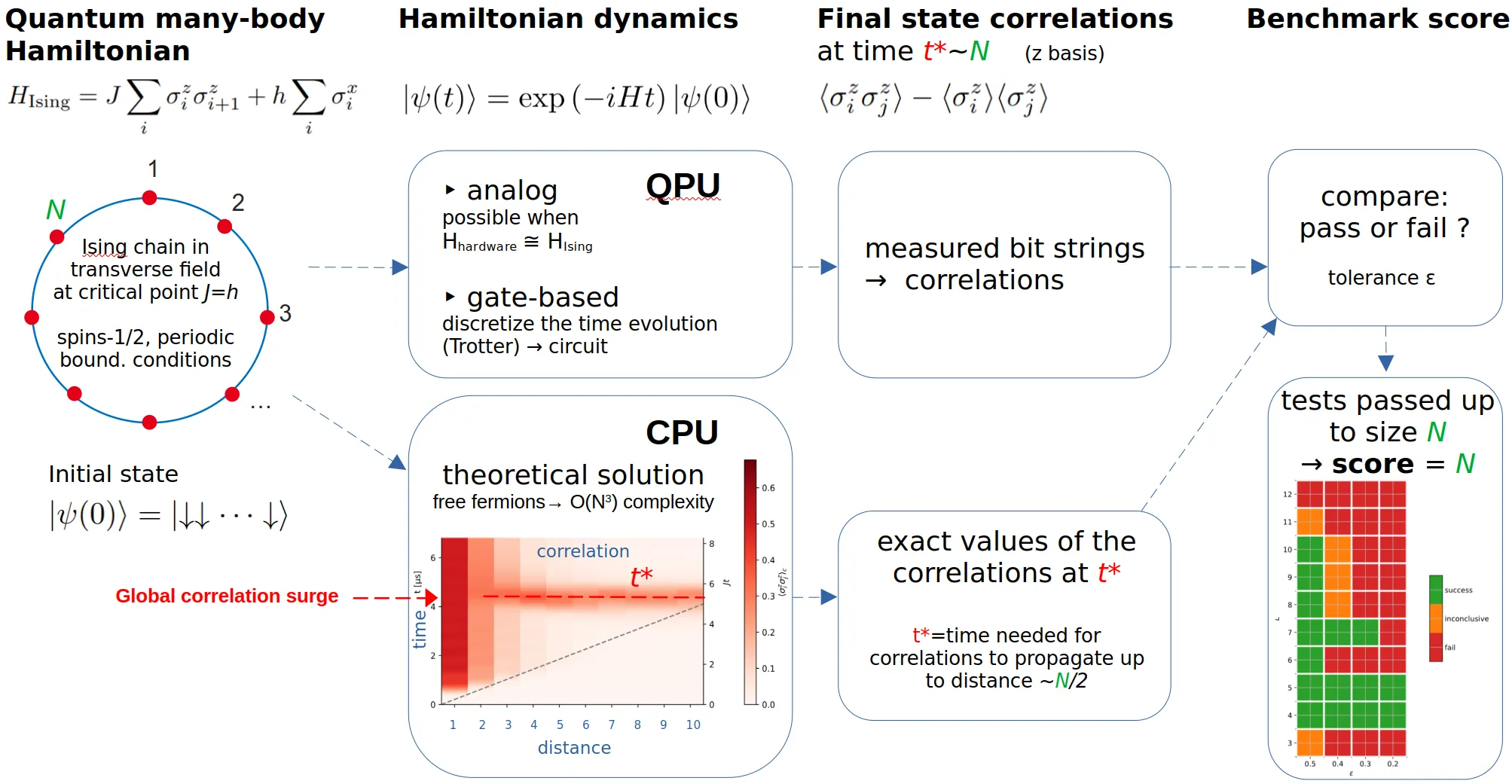
We propose the Many-body Quantum Score (MBQS), a practical and scalable application-level benchmark protocol designed to evaluate the capabilities of quantum processing units (QPUs)--both gate-based and analog--for simulating many-body quantum dynamics. MBQS quantifies performance by identifying the maximum number of qubits with which a QPU can reliably reproduce correlation functions of the transverse-field Ising model following a specific quantum quench. This paper presents the MBQS protocol and highlights its design principles, supported by analytical insights, classical simulations, and experimental data. It also displays results obtained with Ruby, an analog QPU based on Rydberg atoms developed by the Pasqal company. These findings demonstrate MBQS's potential as a robust and informative tool for benchmarking near-term quantum devices for many-body physics.

2601.03461Jan 2026

View

Page 1 of 244