Disordered Systems and Neural Networks

arXiv:cond-mat.dis-nn

Glasses and spin glasses, random graphs, neural networks, localization, stochastic processes.

Trending in Disordered Systems and Neural Networks

Nonequilibrium Thermodynamics of Associative Memory Continuous-Time Recurrent Neural Networks

Continuous-Time Recurrent Neural Networks (CTRNNs) have been widely used for their capacity to model complex temporal behaviour. However, their internal dynamics often remain difficult to interpret. In this paper, we propose a new class of CTRNNs based on Hopfield-like associative memories with asymmetric couplings. This model combines the expressive power of associative memories with a tractable mathematical formalism to characterize fluctuations in nonequilibrium dynamics. We show that this mathematical description allows us to directly compute the evolution of its macroscopic observables (the encoded features), as well as the instantaneous entropy and entropy dissipation of the system, thereby offering a bridge between dynamical systems descriptions of low-dimensional observables and the statistical mechanics of large nonequilibrium networks. Our results suggest that these nonequilibrium associative CTRNNs can serve as more interpretable models for complex sequence-encoding networks.

2511.11150

Nov 2025Disordered Systems and Neural Networks

Related categories:

Mesoscale and Nanoscale Physics Materials Science Other Condensed Matter Quantum Gases Soft Condensed Matter

163 papers

Exact Mobility Edges in a Disorder-Free Dimerized Stark Lattice with Effective Unbounded Hopping

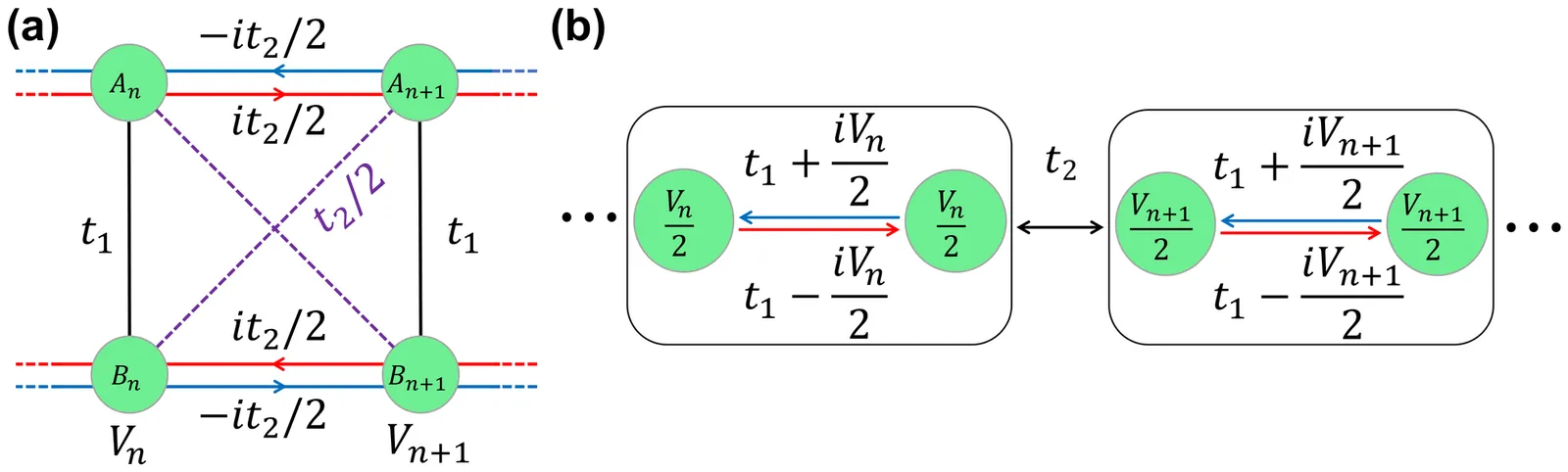
We propose a disorder-free one-dimensional single-particle Hamiltonian hosting an exact mobility edge (ME), placing the system outside the assumptions of no-go theorems regarding unbounded potentials. By applying a linear Stark potential selectively to one sublattice of a dimerized chain, we generate an effective Hamiltonian with unbounded, staggered hopping amplitudes. The unbounded nature of the hopping places the model outside the scope of the Simon-Spencer theorem, while the staggered scaling allows it to evade broader constraints on Jacobi matrices. We analytically derive the bulk spectrum in reciprocal space, identifying a sharp ME where the energy magnitude equals the inter-cell hopping strength. This edge separates a continuum of extended states from two distinct localized branches: a standard unbounded Wannier-Stark ladder and an anomalous bounded branch accumulating at the ME. The existence of extended states is supported by finite-size scaling of the inverse participation ratio up to system sizes $L \sim 10^9$. Furthermore, we propose an experimental realization using photonic frequency synthetic dimensions. Our numerical results indicate that the ME is robust against potential experimental imperfections, including frequency detuning errors and photon loss, establishing a practical path for observing MEs in disorder-free systems.

2601.02259Jan 2026

View

Anderson localisation in spatially structured random graphs

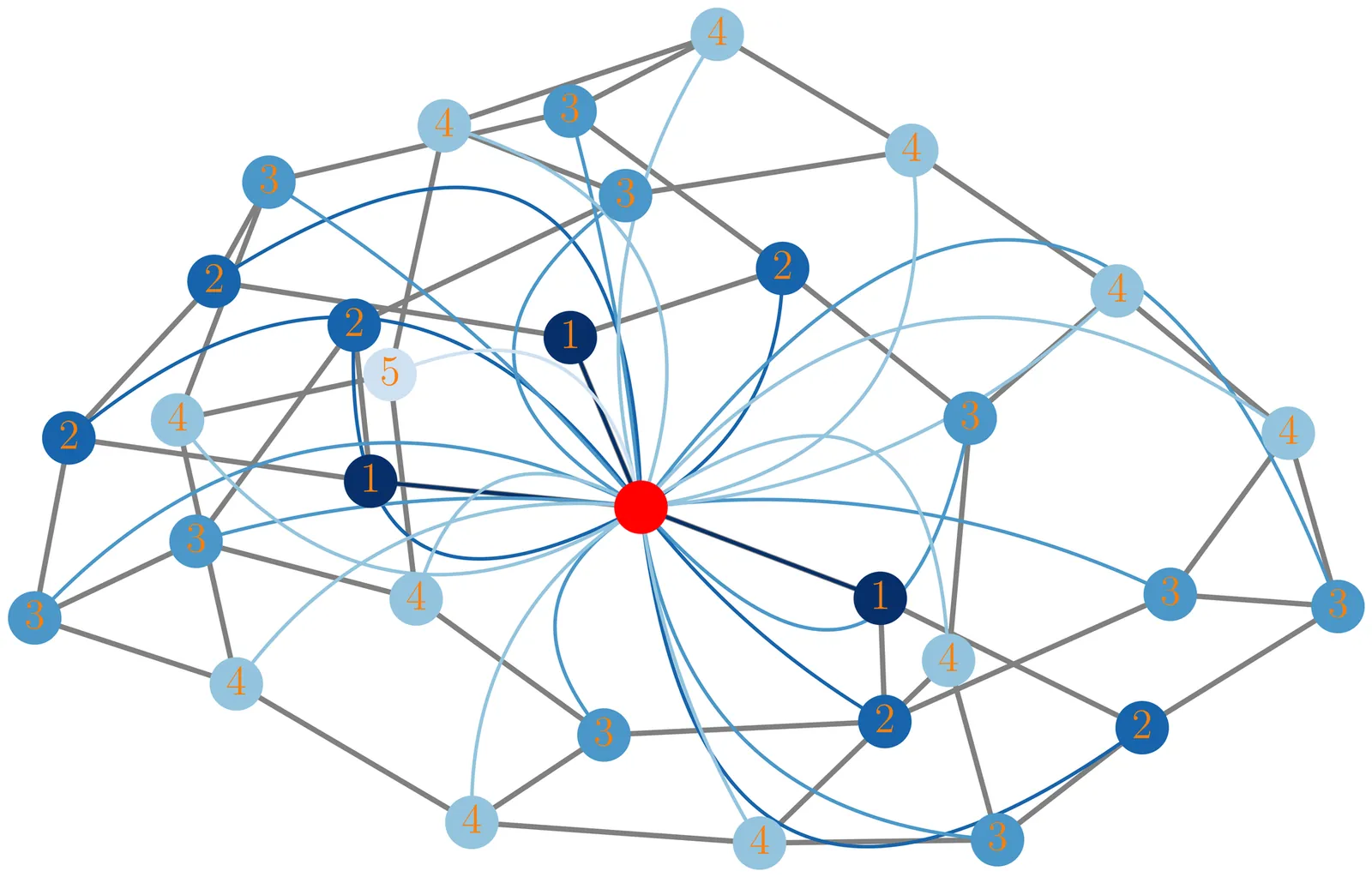
We study Anderson localisation on high-dimensional graphs with spatial structure induced by long-ranged but distance-dependent hopping. To this end, we introduce a class of models that interpolate between the short-range Anderson model on a random regular graph and fully connected models with statistically uniform hopping, by embedding a random regular graph into a complete graph and allowing hopping amplitudes to decay exponentially with graph distance. The competition between the exponentially growing number of neighbours with graph distance and the exponentially decaying hopping amplitude positions our models effectively as power-law hopping generalisation of the Anderson model on random regular graphs. Using a combination of numerical exact diagonalisation and analytical renormalised perturbation theory, we establish the resulting localisation phase diagram emerging from the interplay of the lengthscale associated to the hopping range and the onsite disorder strength. We find that increasing the hopping range shifts the localisation transition to stronger disorder, and that beyond a critical range the localised phase ceases to exist even at arbitrarily strong disorder. Our results indicate a direct Anderson transition between delocalised and localised phases, with no evidence for an intervening multifractal phase, for both deterministic and random hopping models. A scaling analysis based on inverse participation ratios reveals behaviour consistent with a Kosterlitz-Thouless-like transition with two-parameter scaling, in line with Anderson transitions on high-dimensional graphs. We also observe distinct critical behaviour in average and typical correlation functions, reflecting the different scaling properties of generalised inverse participation ratios.

2601.00220Jan 2026

View

Localization-landscape generalized Mott-Berezinskiĭ formula

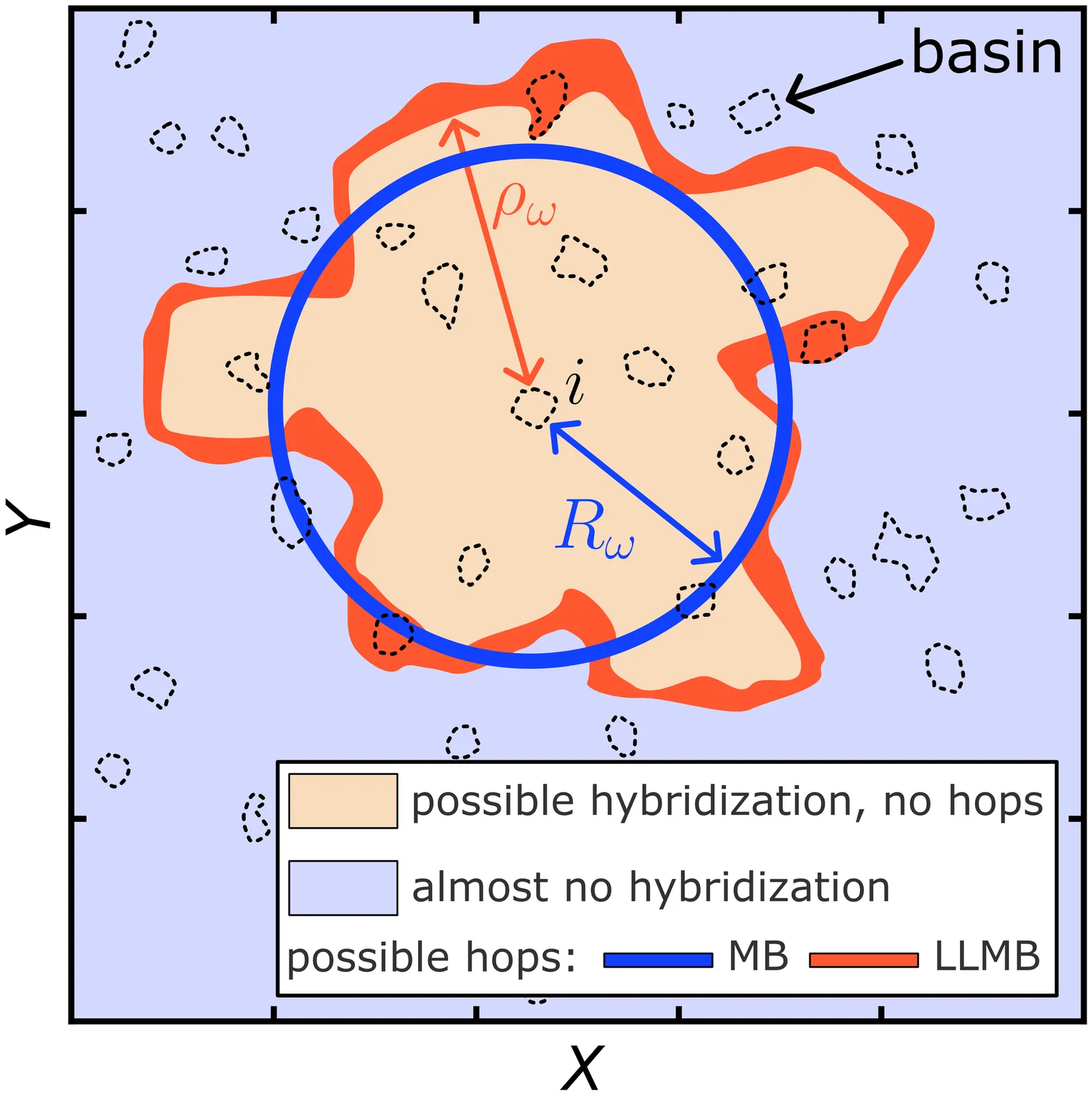
We introduce a conceptual reformulation of the Mott-Berezinskiĭ (MB) theory of low-frequency AC conductivity in disordered systems based on localization landscape theory. Instead of assuming uniform localization and fixed hopping distances, transport is described through an effective potential whose geometry encodes the spatial organization and energy-dependent localization of quantum states. Using the associated Agmon metric, we define a generalized Mott scale that replaces the classical hopping length with a geometric criterion set by the disorder landscape. This framework naturally incorporates strong spatial inhomogeneity and yields the AC conductivity directly from the effective potential. The standard MB result is recovered as a limiting case. Our approach extends the conceptual foundation of MB theory to arbitrary disordered media and energies approaching the mobility edge, providing a unified description of AC transport in complex quantum materials.

2512.23240Dec 2025

View

Density of scattering resonances in a disordered system

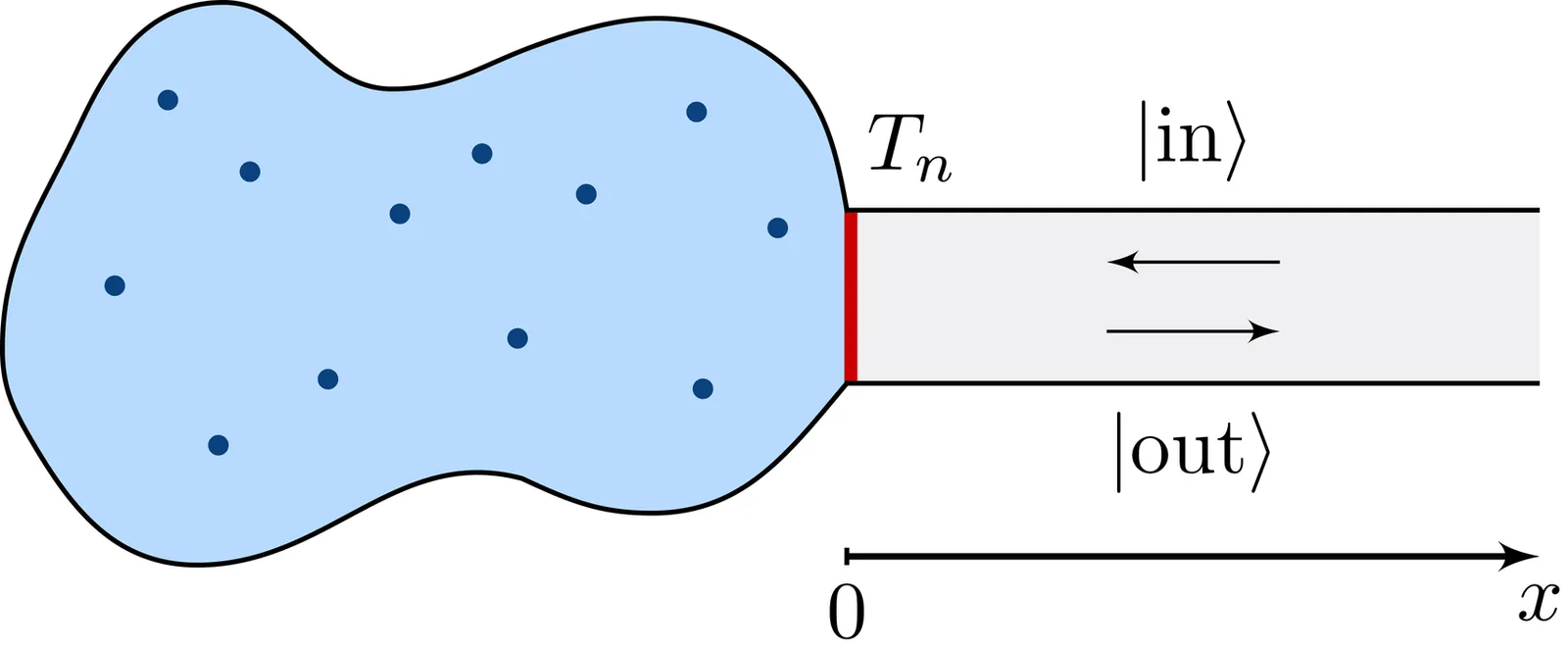
Reflection of particles from a disordered or chaotic medium is characterized by a scattering matrix that can be represented as a superposition of resonances. Each resonance corresponds to an eigenstate inside the medium and has a width related to the decay time of this eigenstate. We develop a general approach to study the distribution function of these resonance widths based on the nonlinear sigma model. We derive an integral representation of the distribution function that works equally well for systems of any symmetry and for any type of coupling to the measuring device. From this integral representation we find explicit analytic expressions for the distribution function in the case of disordered metallic grains. We also compare the analytic results to large-scale numerical simulations and observe their perfect agreement.

2512.18717Dec 2025

View

Consecutive-gap ratio distribution for crossover ensembles

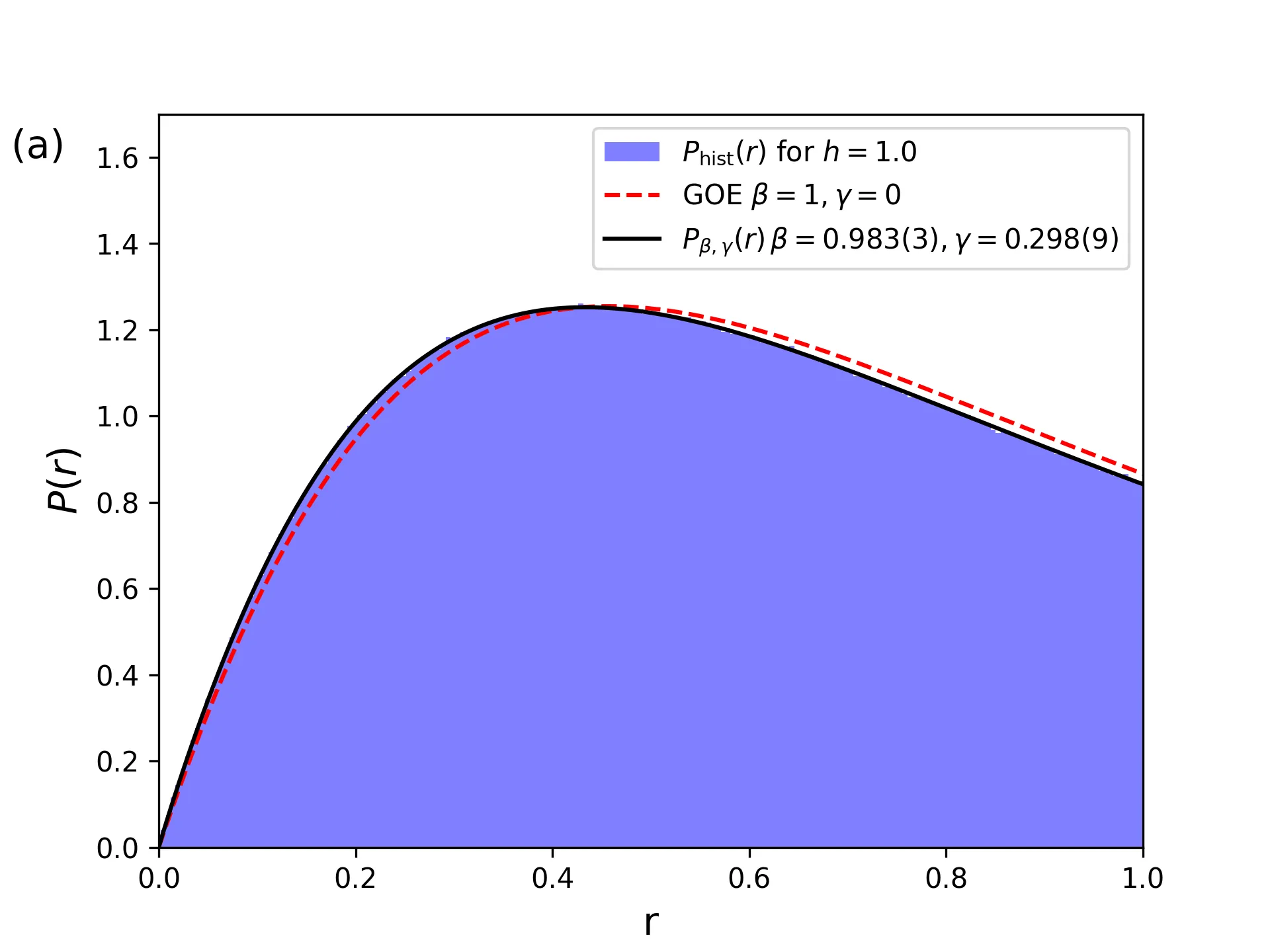
The study of spectrum statistics, such as the consecutive-gap ratio distribution, has revealed many interesting properties of many-body complex systems. Here we propose a two-parameter surmise expression for such distribution to describe the crossover between the Gaussian orthogonal ensemble (GOE) and Poisson statistics. This crossover is observed in the isotropic Heisenberg spin-$1/2$ chain with disordered local field, exhibiting the Many-Body Localization (MBL) transition. Inspired by the analysis of stability in dynamical systems, this crossover is presented as a flow pattern in the parameter space, with the Poisson statistics being the fixed point of the system, which represents the MBL phase. We also analyze an isotropic Heisenberg spin-$1/2$ chain with disordered local exchange coupling and a zero magnetic field. In this case, the system never achieves the MBL phase because of the spin rotation symmetry. This case is more sensitive to finite-size effects than the previous one, and thus the flow pattern resembles a two-dimensional random walk close to its fixed point. We propose a system of linearized stochastic differential equations to estimate this fixed point. We study the continuous-state Markov process that governs the probability of finding the system close to this fixed point as the disorder strength increases. In addition, we discuss the conditions under which the stationary probability distribution is given by a bivariate normal distribution.

2512.15390Dec 2025

View

Unreasonable effectiveness of unsupervised learning in identifying Majorana topology

In unsupervised learning, the training data for deep learning does not come with any labels, thus forcing the algorithm to discover hidden patterns in the data for discerning useful information. This, in principle, could be a powerful tool in identifying topological order since topology does not always manifest in obvious physical ways (e.g., topological superconductivity) for its decisive confirmation. The problem, however, is that unsupervised learning is a difficult challenge, necessitating huge computing resources, which may not always work. In the current work, we combine unsupervised and supervised learning using an autoencoder to establish that unlabeled data in the Majorana splitting in realistic short disordered nanowires may enable not only a distinction between `topological' and `trivial', but also where their crossover happens in the relevant parameter space. This may be a useful tool in identifying topology in Majorana nanowires.

2512.13825Dec 2025

View

Diffusive geodesics wandering in networks of rigid chains

We introduce an ensemble of spatial networks built from the junctions of hindered-rotation chains, incorporating directional correlations between bonds, an aspect ignored in the standard network modeling paradigm. The emergent random networks support geodesics with a wandering exponent $ξ= 1/2$, and a travel-time fluctuation exponent $χ= 0$, consistent with the KPZ relation, yet violating the bound~$χ\geq1/8$ predicted in the Poissonian framework. Transverse deviations follow the Kolmogorov distribution, indicating similarities between Brownian bridge excursions and geodesics in a random medium with correlated edges orientations. These results reveal a new universality class of Euclidean first-passage percolation, where local orientational memory reshapes transport properties and challenges existing bounds for random spatial networks.

2512.04682Dec 2025

View

Tuning Universality in Deep Neural Networks

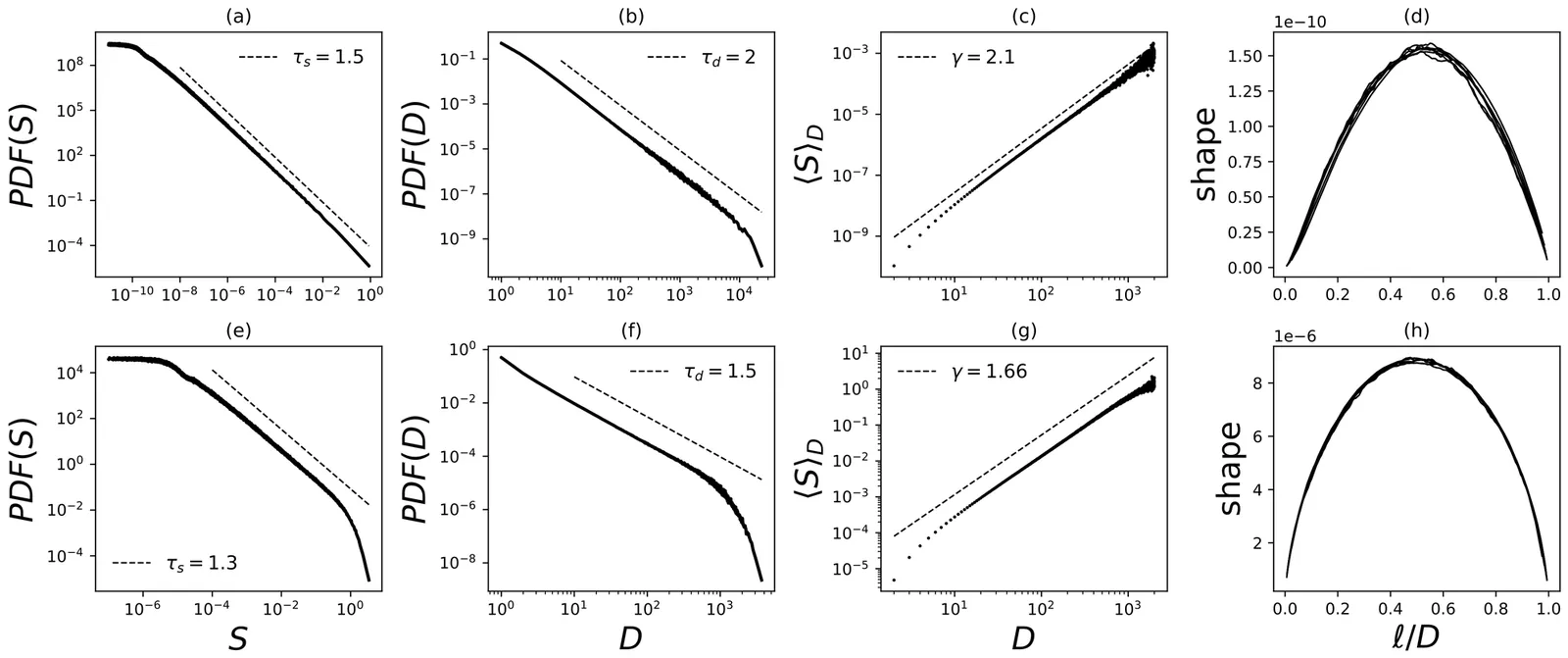
Deep neural networks (DNNs) exhibit crackling-like avalanches whose origin lacks a mechanistic explanation. Here, I derive a stochastic theory of deep information propagation (DIP) by incorporating Central Limit Theorem (CLT)-level fluctuations. Four effective couplings $(r, h, D_1, D_2)$ characterize the dynamics, yielding a Landau description of the static exponents and a Directed Percolation (DP) structure of activity cascades. Tuning the couplings selects between avalanche dynamics generated by a Brownian Motion (BM) in a logarithmic trap and an absorbed free BM, each corresponding to a distinct universality classes. Numerical simulations confirm the theory and demonstrate that activation function design controls the collective dynamics in random DNNs.

2512.00168Nov 2025

View

Local Geometric and Transport Properties of Networks that are Generated from Hyperuniform Point Patterns

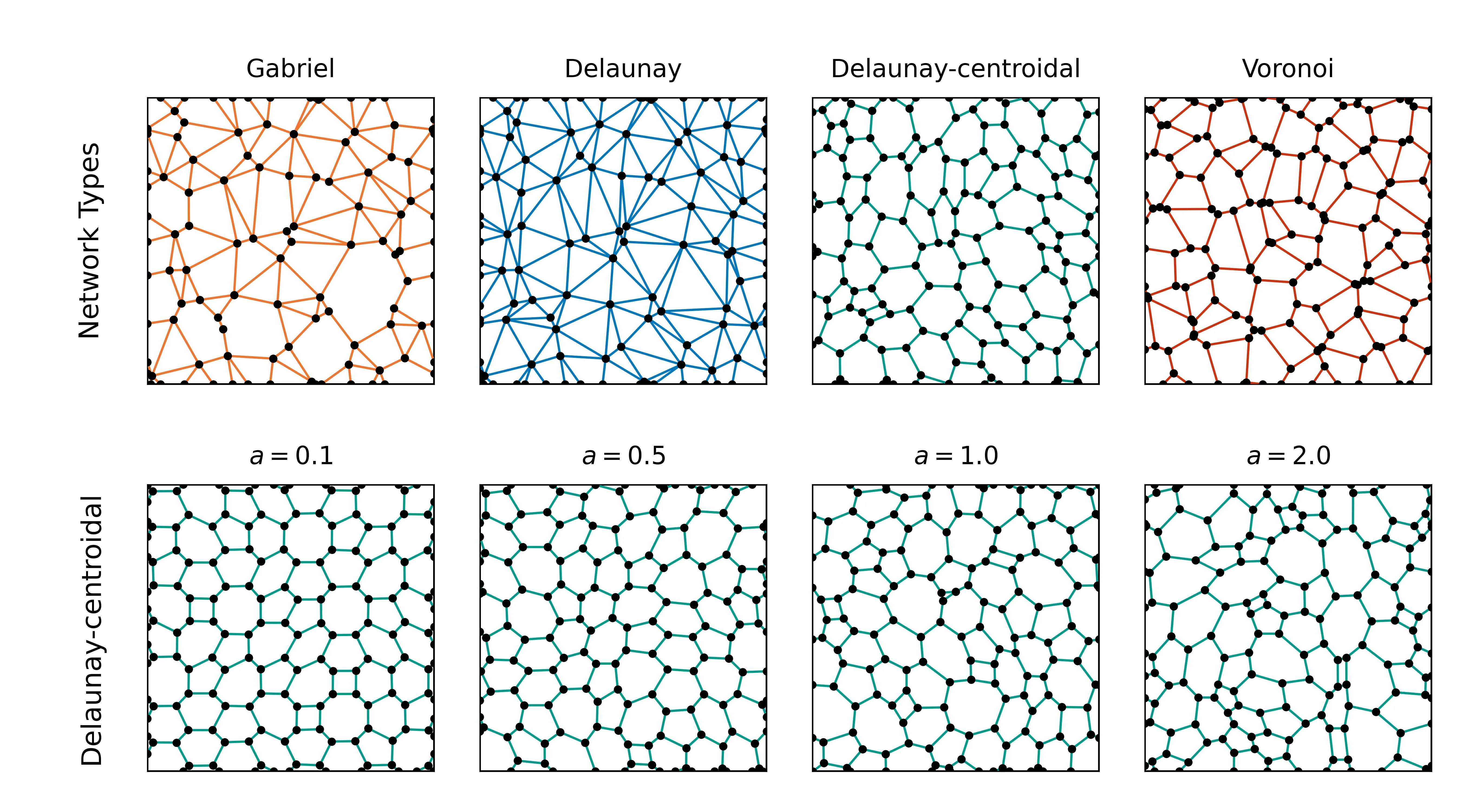
Hyperuniformity, which is a type of long-range order that is characterized by the suppression of long-range density fluctuations in comparison to the fluctuations in standard disordered systems, has emerged as a powerful concept to aid in the understanding of diverse natural and engineered phenomena. In the present paper, we harness hyperuniform point patterns to generate a class of disordered, spatially embedded networks that are distinct from both perfectly ordered lattices and uniformly random geometric graphs. We refer to these networks as \emph{hyperuniform-point-pattern-induced (HuPPI) networks}, and we compare them to their counterpart \emph{Poisson-point-pattern-induced (PoPPI) networks}. By computing the local geometric and transport properties of HuPPI networks, we demonstrate how hyperuniformity imparts advantages in both transport efficiency and robustness. Specifically, we show that HuPPI networks have systematically smaller total effective resistances, slightly faster random-walk mixing times, and fewer extreme-curvature edges than PoPPI networks. Counterintuitively, we also find that HuPPI networks simultaneously have more negative mean Ollivier--Ricci curvatures and smaller total effective resistances than PoPPI networks, indicating that edges with moderately negative curvatures need not create severe bottlenecks to transport. Moreover, HuPPI networks are consistently more robust under both random edge removals and curvature-based targeted edge removals, maintaining larger connected components for larger fractions of removed edges than their PoPPI counterparts. We also demonstrate that the network-generation method strongly influences these properties and in particular that it often overshadows differences that arise from underlying point patterns.

2511.21082Nov 2025

View

Analog Physical Systems Can Exhibit Double Descent

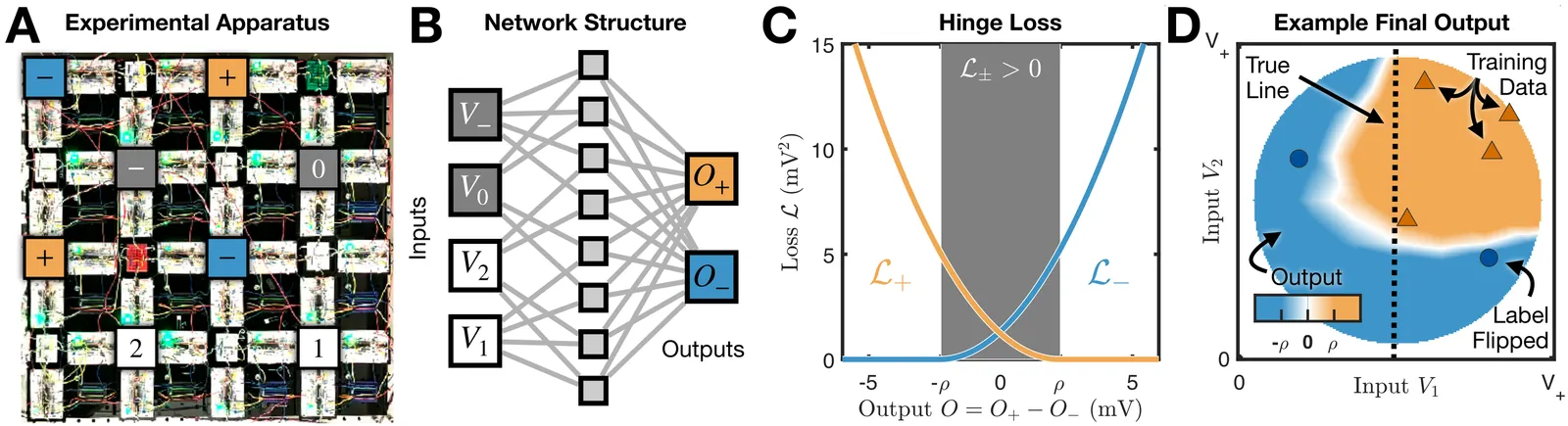
An important component of the success of large AI models is double descent, in which networks avoid overfitting as they grow relative to the amount of training data, instead improving their performance on unseen data. Here we demonstrate double descent in a decentralized analog network of self-adjusting resistive elements. This system trains itself and performs tasks without a digital processor, offering potential gains in energy efficiency and speed -- but must endure component non-idealities. We find that standard training fails to yield double descent, but a modified protocol that accommodates this inherent imperfection succeeds. Our findings show that analog physical systems, if appropriately trained, can exhibit behaviors underlying the success of digital AI. Further, they suggest that biological systems might similarly benefit from over-parameterization.

2511.17825Nov 2025

View

Empirical universality and non-universality of local dynamics in the Sherrington-Kirkpatrick model

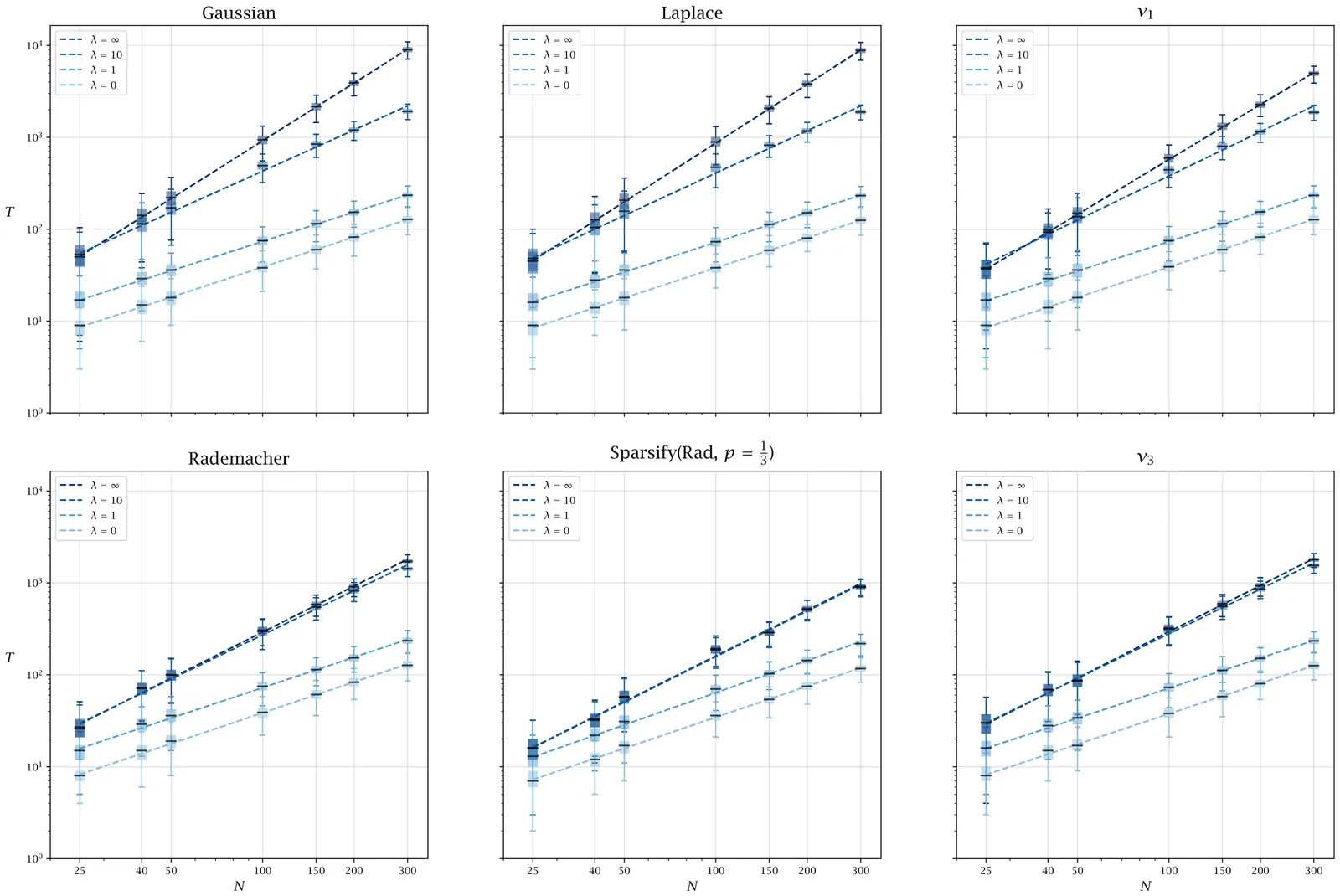
Several recent works have aimed to design algorithms for optimizing the Hamiltonians of spin glass models from statistical physics. While Montanari (2018) eventually gave a sophisticated message-passing algorithm to do this nearly optimally for the Sherrington-Kirkpatrick (SK) model, Parisi (2003) observed earlier that a simple yet unusual algorithm seems to perform just as well: perform local reluctant search, repeatedly making the local adjustment improving the objective function by the smallest possible amount. This is in contrast to the more intuitive local greedy search that repeatedly makes the local adjustment improving the objective by the largest possible amount. We study empirically how the performance of these algorithms depends on the distribution of entries of the coupling matrix in the SK model. We find evidence that, while the runtime of greedy search enjoys universality over a broad range of distributions, the runtime of reluctant search surprisingly is not universal, sometimes depending quite sensitively on the entry distribution. We propose that one mechanism leading to this non-universality is a change in the behavior of reluctant search when the couplings have discrete support on an evenly-spaced grid, and give experimental results supporting this proposal and investigating other properties of a distribution that might affect the performance of reluctant search.

2511.17428Nov 2025

View

Nonequilibrium Thermodynamics of Associative Memory Continuous-Time Recurrent Neural Networks

2511.11150Nov 2025

View

High-Winding-Number Zero-Energy Edge States in Rhombohedral-Stacked Su-Schrieffer-Heeger Multilayers

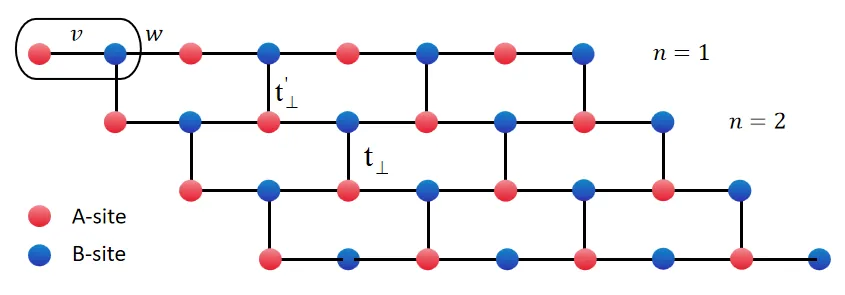
We study the topological properties of rhombohedral-stacked N-layer Su-Schrieffer-Heeger networks with interlayer coupling. We find that these systems exhibit $2N$-fold degenerate zero-energy edge states with winding number $W=N$, providing a direct route to high-winding-number topological phases where $W$ equals the layer number. Using effective Hamiltonian theory and Zak phase calculations, we demonstrate that the winding number scales linearly with $N$ through a layer-by-layer topological amplification mechanism. We introduce the Wigner entropy as a novel detection method for these edge states, showing that topological boundary states exhibit significantly enhanced Wigner entropy compared to bulk states. Our results establish rhombohedral stacking as a systematic approach for engineering high-winding-number topological insulators with potential applications in quantum information processing.

2511.08167Nov 2025

View

Tunable phononic transparency and opacity with isotopic defects

In an isotopically disordered harmonic chain, phonon transmission attenuates exponentially with distance because of multiple scattering by the isotopic defects. We propose a simple method, which is based on the static structure factor, for arranging the isotopic defects to suppress or enhance phonon scattering within a targeted frequency window, resulting in maximization or minimization of phonon transmission. The phononic transparency and opacity effects are demonstrated numerically from the frequency dependence of the transmission coefficient. We briefly discuss how the underlying concept can be extended to the design of aperiodic superlattices to improve or block phononic transmission.

2511.06829Nov 2025

View

Machine learning intermolecular transfer integrals with compact atomic cluster representations

Calculating intermolecular charge transfer integrals in organic semiconductors requires substantial computer resource for each individual calculation. We might alternatively construct a machine learning model for transfer integrals, which model the full six-degrees of freedom for the relative position of dimer pairs, trained on representative calculations for the molecules of interest. Recent developments have produced effective machine learning force fields, which model the total energy of atomic assemblies. We extend the Atomic Cluster Expansion (ACE) with the correct symmetries for transfer (kinetic-energy) integrals. Combined with a spherical harmonic basis makes, this forms a strong inductive bias and makes for a data efficient model. We introduce coarse-grained and heavy-atom representations, and assess the methodology on representative conjugated semiconductors: ethylene, thiophene, and naphthalene.

2511.06551Nov 2025

View

Cluster percolation in the three-dimensional $\pm J$ random-bond Ising model

Based on extensive parallel-tempering Monte Carlo simulations, we investigate the relationship between cluster percolation and equilibrium ordering phenomena in the three-dimensional $\pm J$ random-bond Ising model as one varies the fraction of antiferromagnetic bonds. We consider a range of cluster definitions, most of which are constructed in the space of overlaps between two independent real replicas of the system. In the pure ferromagnet that is contained as a limiting case in the class of problems considered, the relevant percolation point coincides with the thermodynamic ordering transition. For the disordered ferromagnet encountered first on introducing antiferromagnetic bonds and the adjacent spin-glass phase of strong disorder this connection is altered, and one finds a percolation transition above the thermodynamic ordering point that is accompanied by the appearance of /two/ percolating clusters of equal density. Only at the lower (disordered) ferromagnetic or spin-glass transition points the densities of these two clusters start to diverge, thus providing a percolation signature of these thermodynamic transitions. We compare the scaling behavior at this secondary percolation transition with the thermodynamic behavior at the corresponding ferromagnetic and spin-glass phase transitions.

2511.05748Nov 2025

View

Interpretable disorder-promoted synchronization and coherence in coupled laser networks

Coupled lasers offer a promising approach to scaling the power output of photonic devices for applications demanding high frequency precision and beam coherence. However, maintaining coherence among lasers remains a fundamental challenge due to desynchronizing instabilities arising from time delay in the optical coupling. Here, we depart from the conventional notion that disorder is detrimental to synchronization and instead propose an interpretable mechanism through which heterogeneity in the laser parameters can be harnessed to promote synchronization. Our approach allows stabilization of pre-specified synchronous states that, while abundant, are often unstable in systems of identical lasers. The results show that stable synchronization enabling coherence can be frequently achieved by introducing intermediate levels of random mismatches in any of several laser constructive parameters. Our results establish a principled framework for enhancing coherence in large laser networks, offering a robust strategy for power scaling in photonic systems.

2511.047491Nov 2025

View

On the supra-linear storage in dense networks of grid and place cells

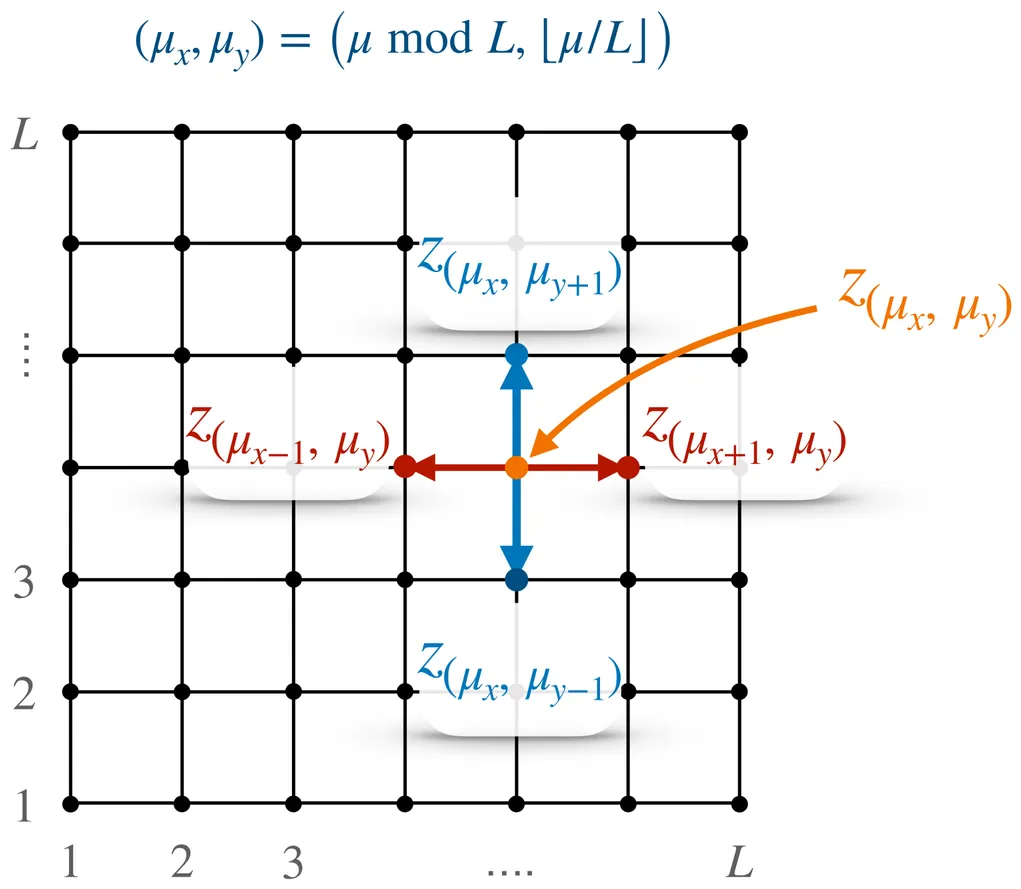
Place-cell networks, typically forced to pairwise synaptic interactions, are widely studied as models of cognitive maps: such models, however, share a severely limited storage capacity, scaling linearly with network size and with a very small critical storage. This limitation is a challenge for navigation in 3-dimensional space because, oversimplifying, if encoding motion along a one-dimensional trajectory embedded in 2-dimensions requires $O(K)$ patterns (interpreted as bins), extending this to a 2-dimensional manifold embedded in a 3-dimensional space -- yet preserving the same resolution -- requires roughly $O(K^2)$ patterns, namely a supra-linear amount of patterns. In these regards, dense Hebbian architectures, where higher-order neural assemblies mediate memory retrieval, display much larger capacities and are increasingly recognized as biologically plausible, but have never linked to place cells so far. Here we propose a minimal two-layer model, with place cells building a layer and leaving the other layer populated by neural units that account for the internal representations (so to qualitatively resemble grid cells in the MEC of mammals): crucially, by assuming that each place cell interacts with pairs of grid cells, we show how such a model is formally equivalent to a dense Battaglia-Treves-like Hebbian network of grid cells only endowed with four-body interactions. By studying its emergent computational properties by means of statistical mechanics of disordered systems, we prove -- analytically -- that such effective higher-order assemblies (constructed under the guise of biological plausibility) can support supra-linear storage of continuous attractors; furthermore, we prove -- numerically -- that the present neural network is capable of recognition and navigation on general surfaces embedded in a 3-dimensional space.

2511.02441Nov 2025

View

2511.01105

Glass Patterns in Twisted Disordered Crystals

Twisting and stacking two copies of a 2D crystal can produce a long-wavelength periodic interference pattern known as a moiré pattern. Performing the same procedure with an aperiodic structure instead generates a single moiré spot at the rotation center, known as a Glass pattern. We explore the implications of these patterns across a variety of models: they allow measurement of microscopic parameters from mesoscopic resistivity measurements; they generate an impurity that modifies the properties of a moiré lattice at the rotation center; and they allow for domain formation in amorphous magnets. These results establish Glass patterns as a generic feature of twisted disordered systems and provide a framework for future theoretical and experimental exploration.

2511.01105Nov 2025

View

Correspondence Between Ising Machines and Neural Networks

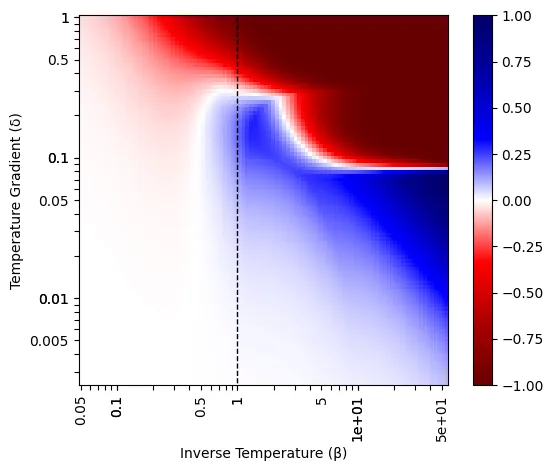
Computation with the Ising model is central to future computing technologies like quantum annealing, adiabatic quantum computing, and thermodynamic classical computing. Traditionally, computed values have been equated with ground states. This paper generalizes computation with ground states to computation with spin averages, allowing computations to take place at high temperatures. It then introduces a systematic correspondence between Ising devices and neural networks and a simple method to run trained feed-forward neural networks on Ising-type hardware. Finally, a mathematical proof is offered that these implementations are always successful.

2511.00746Nov 2025

View

Page 1 of 9