Soft Condensed Matter

arXiv:cond-mat.soft

Polymers, liquid crystals, membranes, colloids, foams, active matter.

Trending in Soft Condensed Matter

Orientational lineage memory and mechanical ordering during diffusion-limited growth

Growth and shape formation in crowded multicellular assemblies arise from the interplay of chemical gradients, single-cell expansion and mechanical interactions, making it essential to understand how these processes jointly shape collective organization. Using a particle-based model that resolves nutrient fields as well as cellular orientations and their inheritance, we investigate how orientational order emerges within expanding fronts whose morphology is set by nutrient limitation. We identify a transition in nematic order controlled by front morphology, with orientational memory influencing alignment only on one side of this transition. Under strong inheritance, orientational order varies non-monotonically: both thin active layers (fingering morphologies) and thick active layers (flat fronts) produce strong alignment, whereas intermediate cases are less ordered. Analysis of velocities, reorientation statistics, and stress anisotropies shows that this behavior reflects a shift from inheritance-dominated to mechanically driven alignment that overrides lineage memory. The resulting differences in front speed produce a fitness advantage of orientational memory only in the diffusion-limited, memory-dominated regime. These findings elucidate how nutrient supply, mechanical interactions, and single-cell expansion together shape self-organization during growth.

2512.01981

Dec 2025Soft Condensed Matter

Related categories:

Disordered Systems and Neural Networks Mesoscale and Nanoscale Physics Materials Science Other Condensed Matter Quantum Gases

363 papers

Mechanics of axis formation in $\textit{Hydra}$

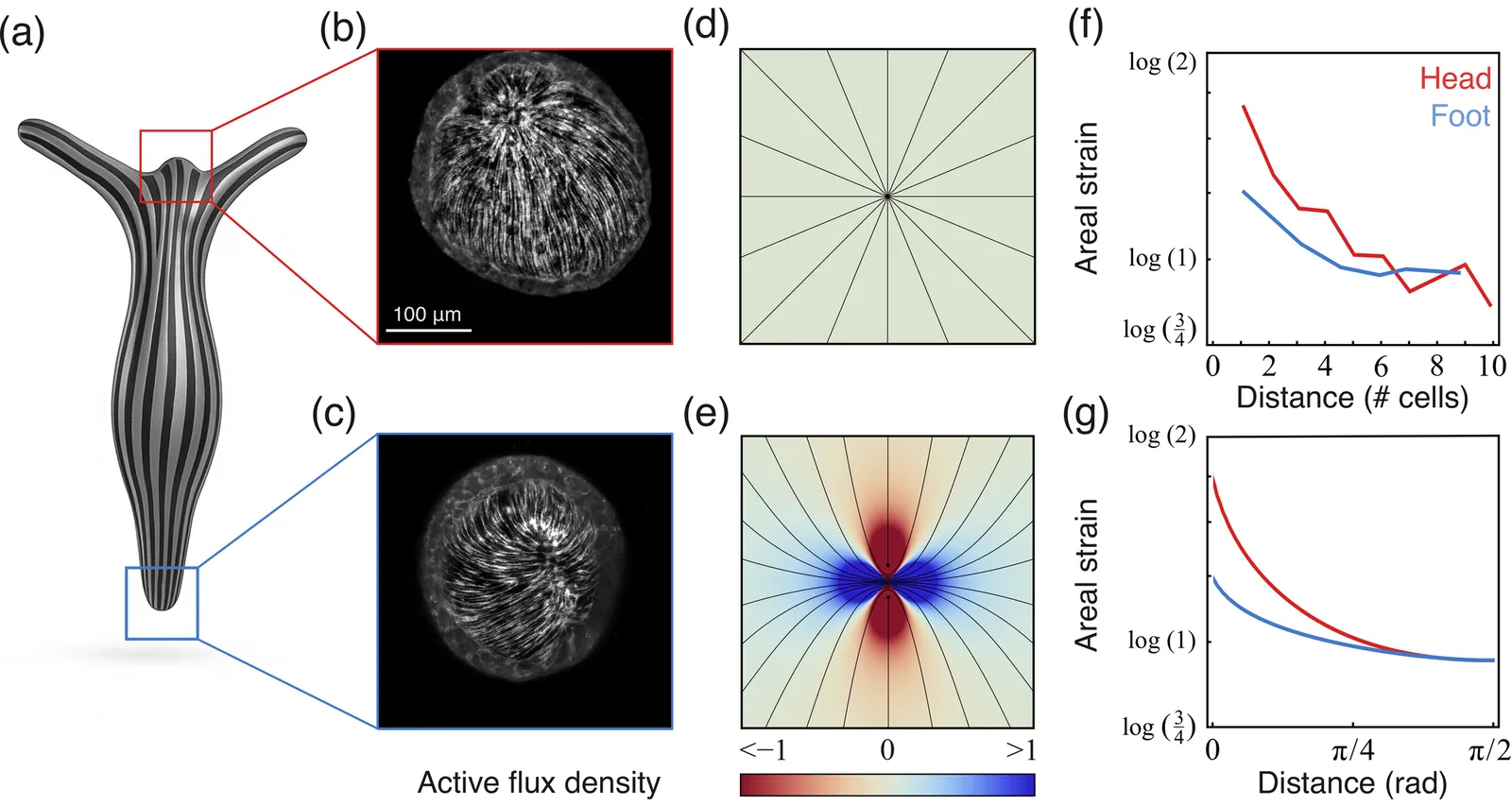
The emergence of a body axis is a fundamental step in the development of multicellular organisms. In simple systems such as $\textit{Hydra}$, growing evidence suggests that mechanical forces generated by collective cellular activity play a central role in this process. Here, we explore a physical mechanism for axis formation based on the coupling between active stresses and tissue elasticity. We analyse the elastic deformation induced by activity-generated stresses and show that, owing to the spherical topology of the tissue, forces globally condense toward configurations in which both elastic strain and nematic defect localise at opposite poles. These mechanically selected states define either a polar or apolar head-food axis. To characterize the condensed regime, we introduce a compact parametrization of of the active force and flux distributions, enabling analytical predictions and direct comparison with experiments. Using this framework, we calculate experimentally relevant observables, including areal strain, lateral pressure, and normal displacements during muscular contraction, as well as the detailed structure of topological defect complexes in head and foot regions. Together, our results identify a mechanical route by which active tissues can spontaneously break symmetry at the organismal scale, suggesting a general physical principle underlying body-axis specification during morphogenesis.

2601.05220Jan 2026

View

Mesoscale flows in active baths dictate the dynamics of semi-flexible filaments

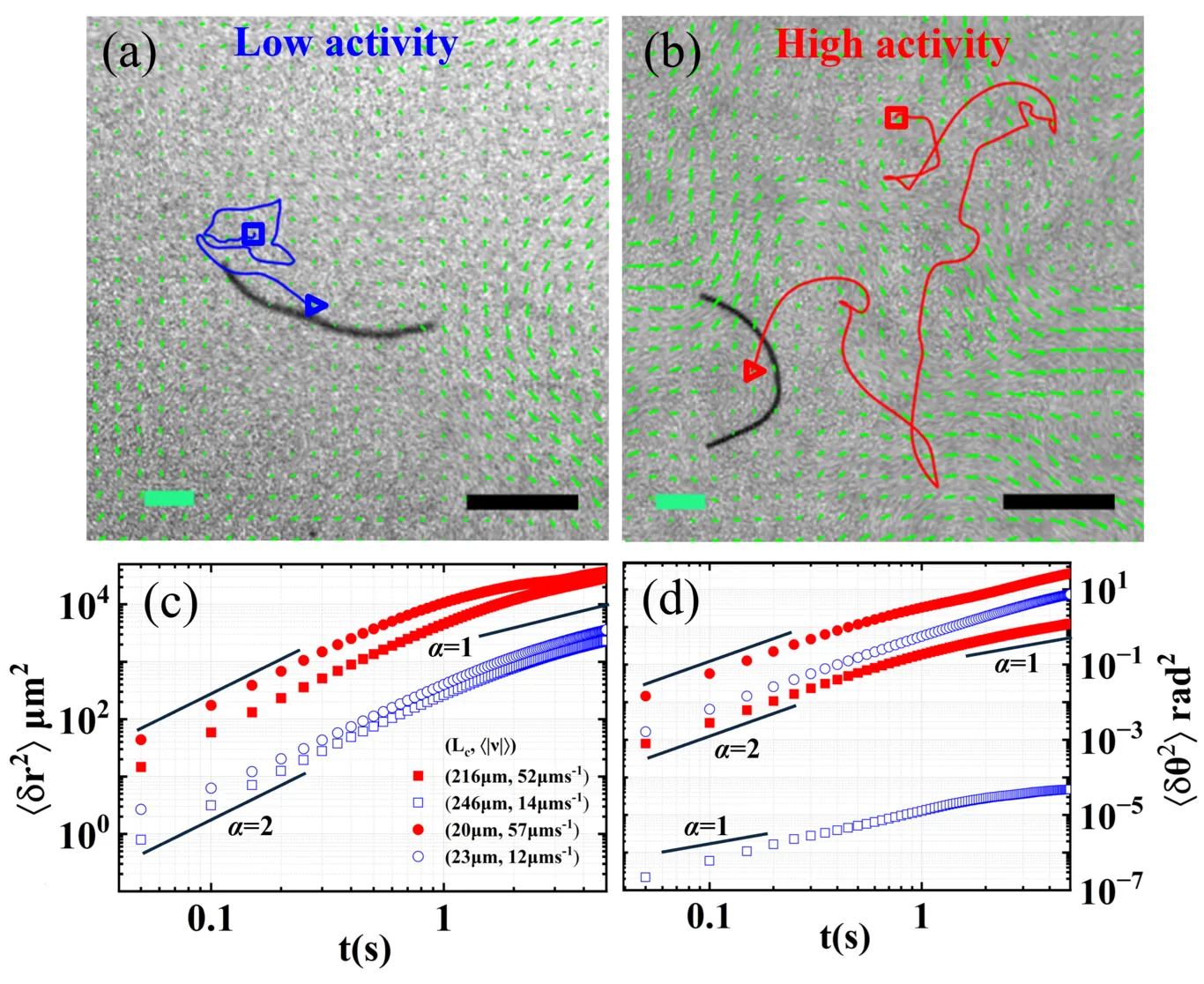
Semi-flexible filaments in living systems are constantly driven by active forces that often organize into mesoscale coherent flows. Although theory and simulations predict rich filament dynamics, experimental studies of passive filaments in collective active baths remain scarce. Here we present an experimental study on passive colloidal filaments confined to the air-liquid interface beneath a free-standing, quasi-two-dimensional bacterial film featuring jet-like mesoscale flows. By varying filament contour length and bacterial activity, we demonstrate that filament dynamics are governed by its length relative to the characteristic size of the bath. Filaments shorter than the jet width exhibit greatly enhanced translation and rotation with minimal deformation, while long filaments show dramatic deformation but less enhanced transport. We explain our findings through the competition between the active viscous drag of the bath and passive elastic resistance of the filaments, using a modified elastoviscous number that considers the mesoscale flows.

2601.04420Jan 2026

View

2601.04026

Transport properties in a model of confined granular mixtures at moderate densities

This work derives the Navier--Stokes hydrodynamic equations for a model of a confined, quasi-two-dimensional, $s$-component mixture of inelastic, smooth, hard spheres. Using the inelastic version of the revised Enskog theory, macroscopic balance equations for mass, momentum, and energy are obtained, and constitutive equations for the fluxes are determined through a first-order Chapman--Enskog expansion. As for elastic collisions, the transport coefficients are given in terms of the solutions of a set of coupled linear integral equations. Approximate solutions to these equations for diffusion transport coefficients and shear viscosity are achieved by assuming steady-state conditions and considering leading terms in a Sonine polynomial expansion. These transport coefficients are expressed in terms of the coefficients of restitution, concentration, the masses and diameters of the mixture's components, and the system's density. The results apply to moderate densities and are not limited to particular values of the coefficients of restitution, concentration, mass, and/or diameter ratios. As an application, the thermal diffusion factor is evaluated to analyze segregation driven by temperature gradients and gravity, providing criteria that distinguish whether larger particles accumulate near the hotter or colder boundaries.

2601.04026Jan 2026

View

Kinetic theory of dilute granular gases with hard-core and inverse power-law potentials under uniform shear flow: comparison with simplified model

We develop a kinetic-theory framework to investigate the steady rheology of a dilute gas interacting via a repulsive potential under uniform shear flow. Starting from the Boltzmann equation with a restitution coefficient that depends on the impact velocity and potential strength, we derive evolution equations for the stress tensor based on Grad's moment expansion. The resulting expressions for the collisional rates and transport coefficients are fitted with simple analytical functions that capture their temperature dependence over a wide range of shear rates. Comparison with direct simulation Monte Carlo (DSMC) results shows excellent quantitative agreement for the shear stress, temperature anisotropy, and steady viscosity. We also analyze the velocity distribution functions, revealing that the system remains nearly Maxwellian even under strong shear.

2601.03472Jan 2026

View

Polymorph Selection in Charged Colloids in the Second Nucleation Step

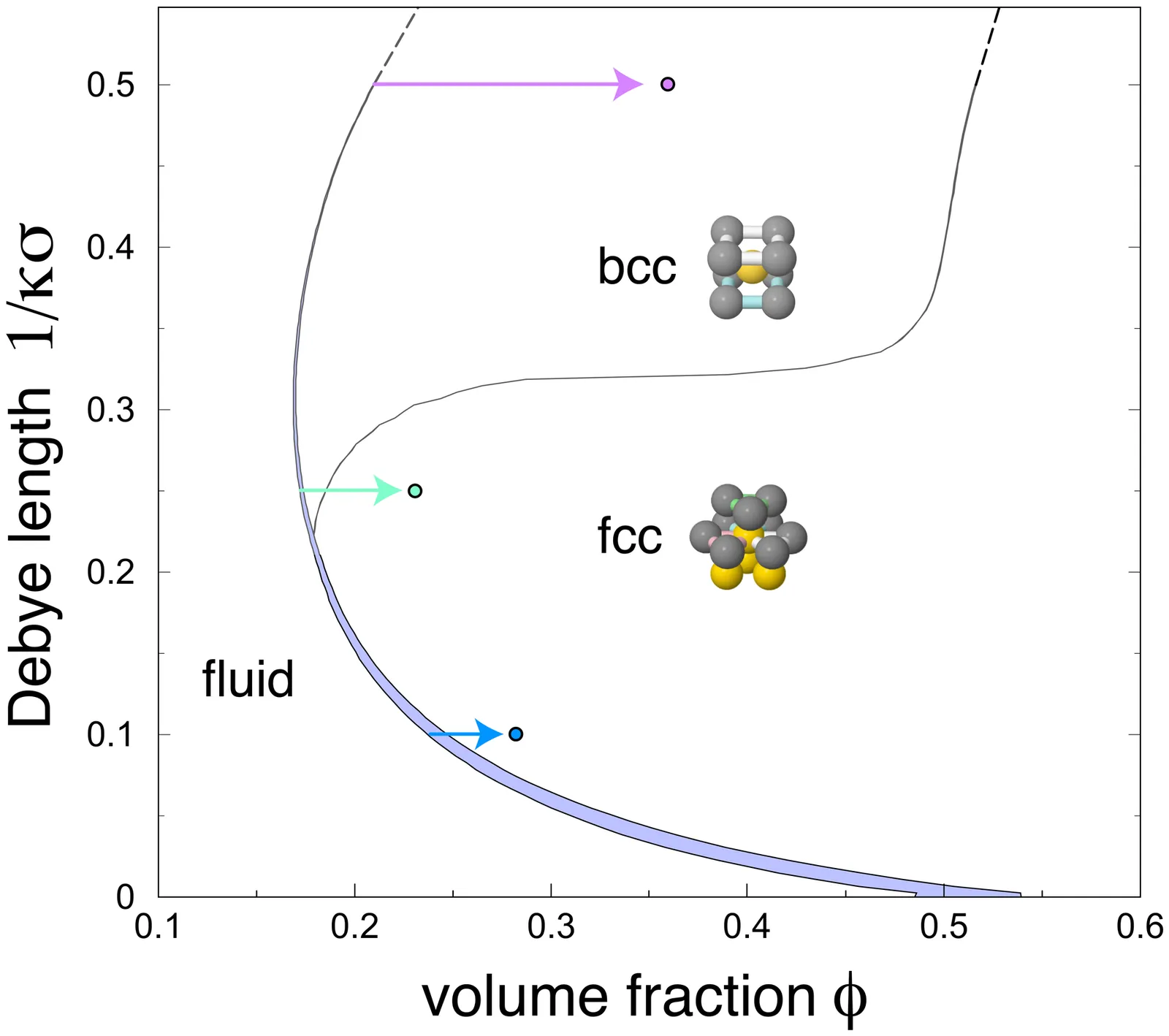
We study polymorph selection in a model of charged colloids, with a focus on the higher-order structure prior to and during nucleation. Specifically, we carry out molecular dynamics simulations of a repulsive Yukawa system with a slightly softened (Weeks-Chandler-Andersen) core. We consider the case where the interaction is long-ranged and the BCC crystal is stable, and also intermediate- and short-ranged cases where the FCC crystal is stable. We use two methods for structure identification, the topological cluster classification (TCC) [A. Malins et al., J. Chem. Phys. 139, 234506 (2013)] and the bond orientational order parameter analysis of W. Lechner and C. Dellago [J. Chem. Phys.129, 114707 (2008)]. Under conditions of high supersaturation, appropriate to experiments with colloids, we find that the system forms a precursor state in which the particles are hexagonally ordered. ~That is to say, the precursors are indistinguishable from an HCP crystal using the bond orientational order parameters. This ordering occurs at state points both when the body-centred cubic crystal is the stable phase, and also when the face-centred cubic crystal is stable. In all cases, the stable polymorph forms from the precursor phase in a second stage. Although at freezing, the fluid is very much more ordered when the interactions are short-ranged (when FCC is stable), at the supersaturations where nucleation occurs in our simulations, the higher-order structure of the metastable fluids is almost identical for the long-, short-, and intermediate-ranged systems when measured with the TCC.

2601.03419Jan 2026

View

Protein-Water Energy Transfer via Anharmonic Low-Frequency Vibrations

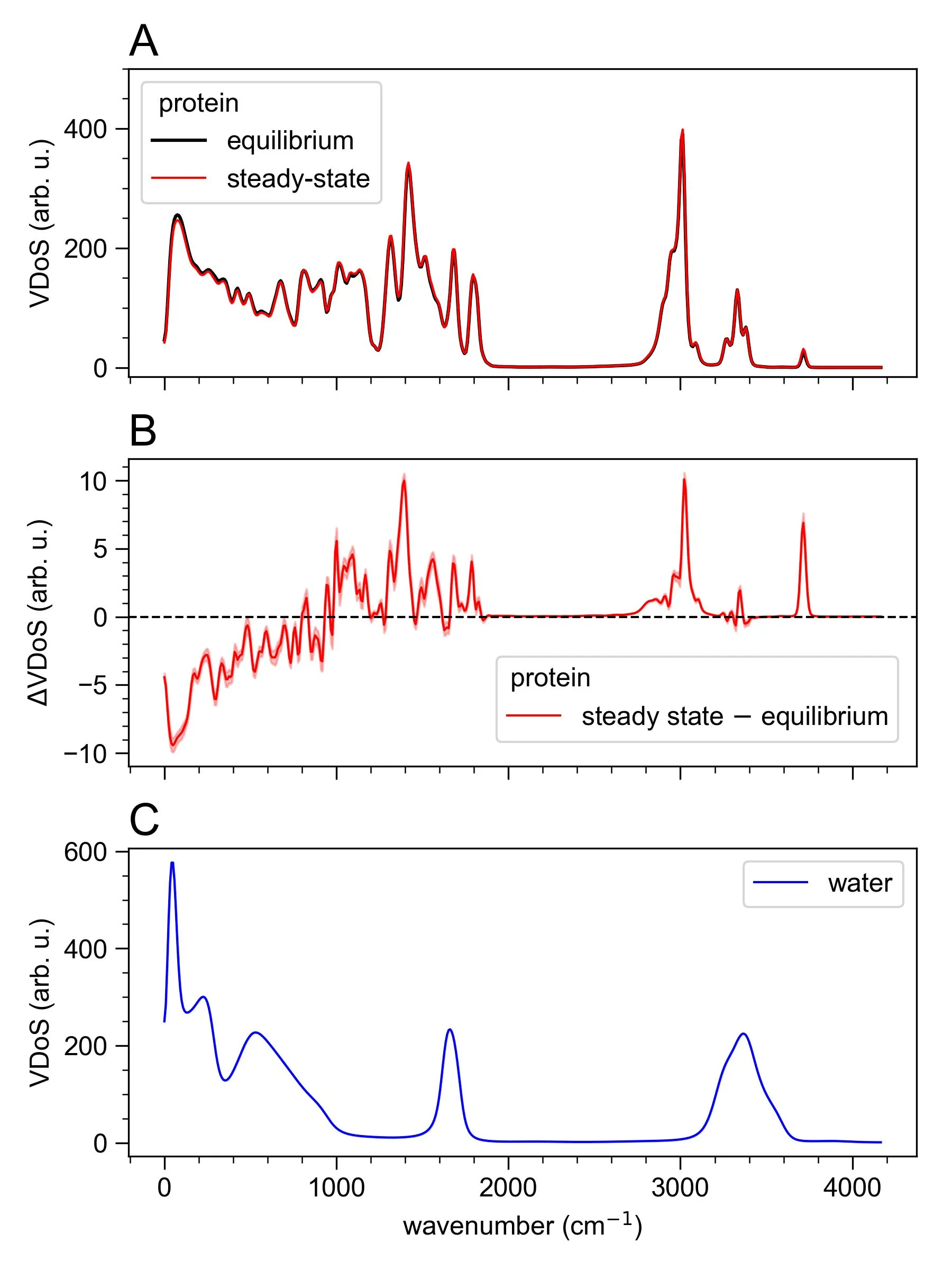
Heat dissipation is ubiquitous in living systems, which constantly convert distinct forms of energy into each other. The transport of thermal energy in liquids and even within proteins is well understood but kinetic energy transfer across a heterogeneous molecular boundary provides additional challenges. Here, we use atomistic molecular dynamics simulations under steady-state conditions to analyze how a protein dissipates surplus thermal energy into the surrounding solvent. We specifically focus on collective degrees of freedom that govern the dynamics of the system from the diffusive regime to mid-infrared frequencies. Using a fully anharmonic analysis of molecular vibrations, we analyzed their vibrational spectra, temperatures, and heat transport efficiencies. We find that the most efficient energy transfer mechanisms are associated with solvent-mediated friction. However, this mechanism only applies to a small number of degrees of freedom of a protein. Instead, less efficient vibrational energy transfer in the far-infrared dominates heat transfer overall due to a large number of vibrations in this frequency range. A notable by-product of this work is a highly sensitive measure of deviations from energy equi-partition in equilibrium systems, which can be used to analyze non-ergodic properties.

2601.02699Jan 2026

View

Fluids at an electrostatically active surface: Optimum in interfacial friction and electrohydrodynamic drag

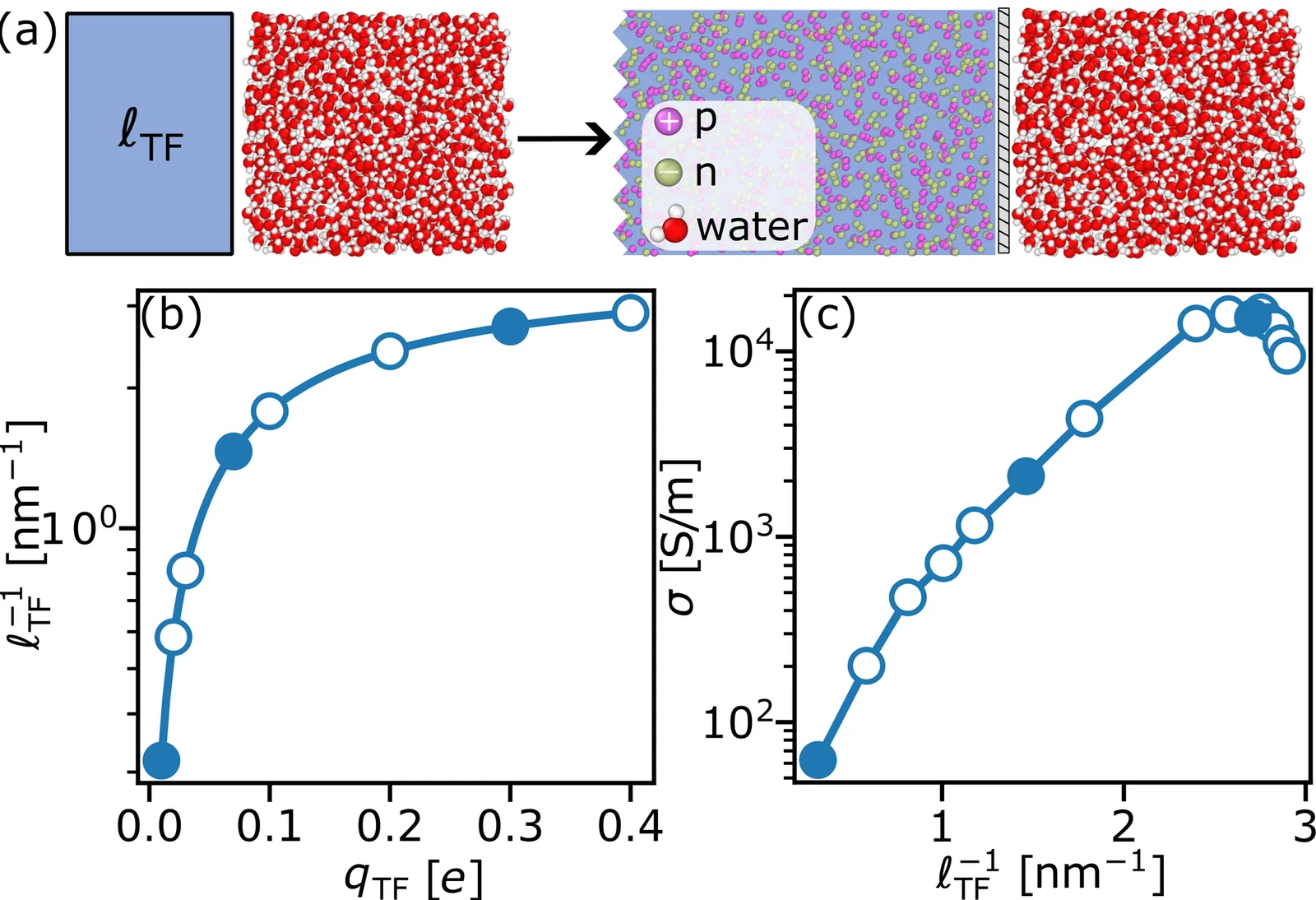
While fluids near a solid surface are at the core of applications in energy storage/conversion, electrochemistry/electrowetting and adsorption/catalysis, their nanoscale behavior remains only partially deciphered. Beyond conventional effects (e.g. adsorption/reaction, interfacial transport, phase transition shifts), recent experimental and theoretical studies on metallic surfaces have unraveled exotic peculiarities such as complex electrostatic screening, unexpected wetting transition, and interfacial quantum friction. These novel features require developing and embarking new tools to tackle the coupling between charge relaxation in the metal and molecular behavior in the vicinal fluid. Here, using the concept of Virtual Thomas-Fermi fluids, we employ a molecular simulation approach to investigate interfacial transport of fluid molecules and metal charge carriers at their interface--including the underlying electrostatically-driven dynamic friction and the coupling between charge current/hydrodynamic flow (the so-called electrohydrodynamic drag). While conventional numerical techniques consider either insulating materials or metallic materials described as polarizable, non-conducting media, our atom-scale strategy provides an effective yet realistic description of the solid excitation spectrum--including charge relaxation modes and conductivity. By applying this approach to water near metallic surfaces of various electrostatic screening lengths, we unveil a non-monotonous dependence of the fluid/solid friction on the metallicity with a maximum occurring as the charge dynamic structure factors of the solid and fluid strongly overlap. Moreover, we report a direct observation of the electrohydrodynamic drag which arises from the momentum transfer between the solid and liquid through dynamic electrostatic interactions and the underlying interfacial friction.

2601.02539Jan 2026

View

Beyond the Static Kuhn Length: Conformational Substructures and Relaxation Dynamics in Flexible Chains

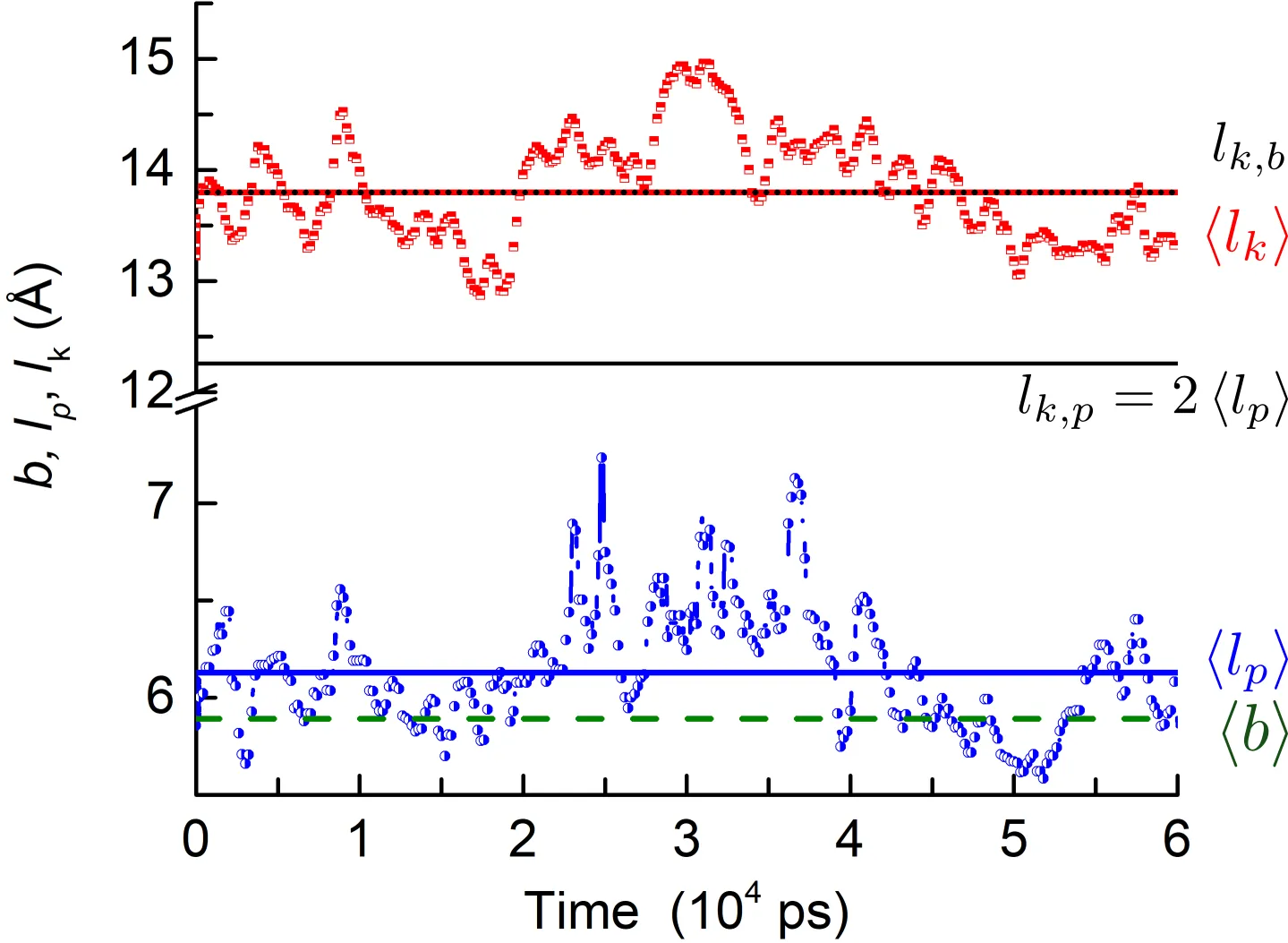
The statistical "monomer-based" segment length $b$ and the Kuhn length $l_k$ are central to polymer physics, yet the minimal size required for a truly statistical segment - Gaussian, uncorrelated, and valid as an entropic spring - is not rigorously established. Using atomistic simulations of entangled polyethylene, we re-evaluate these foundational quantities. By fitting end-to-end distance distributions of C--C bond blocks and validating with higher-moment analyses, we identify for the first time the minimal sizes corresponding to a statistical segment and an entropic spring. A single Kuhn segment (approximately 11 bonds) is the smallest statistically uncorrelated unit, but its distance distribution is strongly non-Gaussian, while the monomer-based segment $b$, used in rheology and classical tube-theory formulations, is not statistical at all. True Gaussianity emerges only for blocks containing multiple Kuhn segments. At the Kuhn scale, we uncover a previously unresolved conformational heterogeneity. Each segment samples a broad range of conformations, from coiled (approximately 4~Å) to extended (approximately 14~Å), giving rise to three distinct substructures: aligned chain segments (ACS), random conformational sequences (RCS), and chain ends (CE). These exhibit distinct dynamical signatures. ACS relax with a stretched-exponential exponent $β\approx 0.5$, consistent with quasi-one-dimensional, defect-mediated localized modes, whereas RCS and CE relax with $β\approx 0.7$. By connecting these results to localized-mode theory and continuous-time random-walk models, we provide a molecular interpretation of stretched-exponential relaxation in polymer melts.

2601.02127Jan 2026

View

Information supercurrents and spin waves in chiral active matter: Universality of the Landau-Lifshitz-Gilbert equation

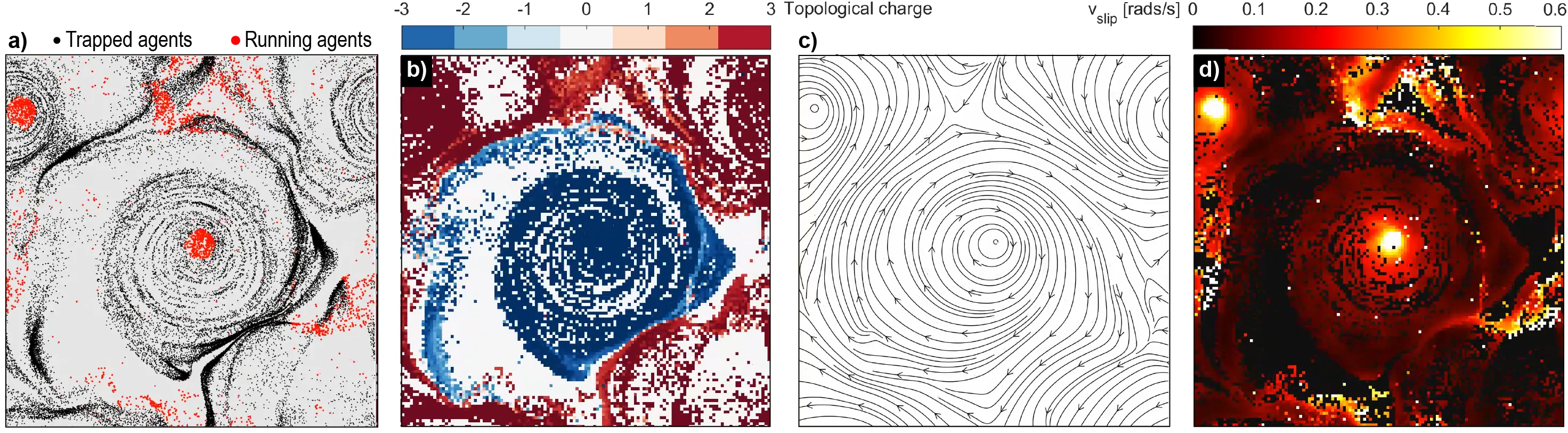
Recent minimalist modeling indicates that overdamped polar chiral active matter can support inviscid Euler turbulence, despite the system's strictly dissipative microscopic nature. In this article, we establish the statistical mechanical foundation for this emergent inertial regime by deriving a formal isomorphism between the model's agent dynamics and the overdamped Langevin equation for disordered Josephson junctions. We identify the trapped agent state as carrying non-dissipative phase rigidity supercurrents, a mapping we confirm empirically by demonstrating a disorder-broadened Adler-Ohmic crossover in the system's slip velocity. Generalizing this framework to three dimensions ($S^1\to S^2$), we show that polar alignment on the unit sphere is geometrically equivalent to the Gilbert damping term in spintronics, and that the two-dimensional Kuramoto coupling term naturally appears in the tangent-plane projection of spin relaxation. This constraint generates inertial spin waves (ferromagnetic magnons) from the overdamped active bath, recovering the macroscopic transport predicted by Toner-Tu theory without invoking microscopic inertia. Our results show that all polar chiral agents who seek to align on the unit sphere strictly constitute a dissipative spintronic fluid, where phase gradient transport is ensured by the Goldstone modes of the underlying broken symmetry.

2512.168841Dec 2025

View

Intelligent matter consisting of active particles

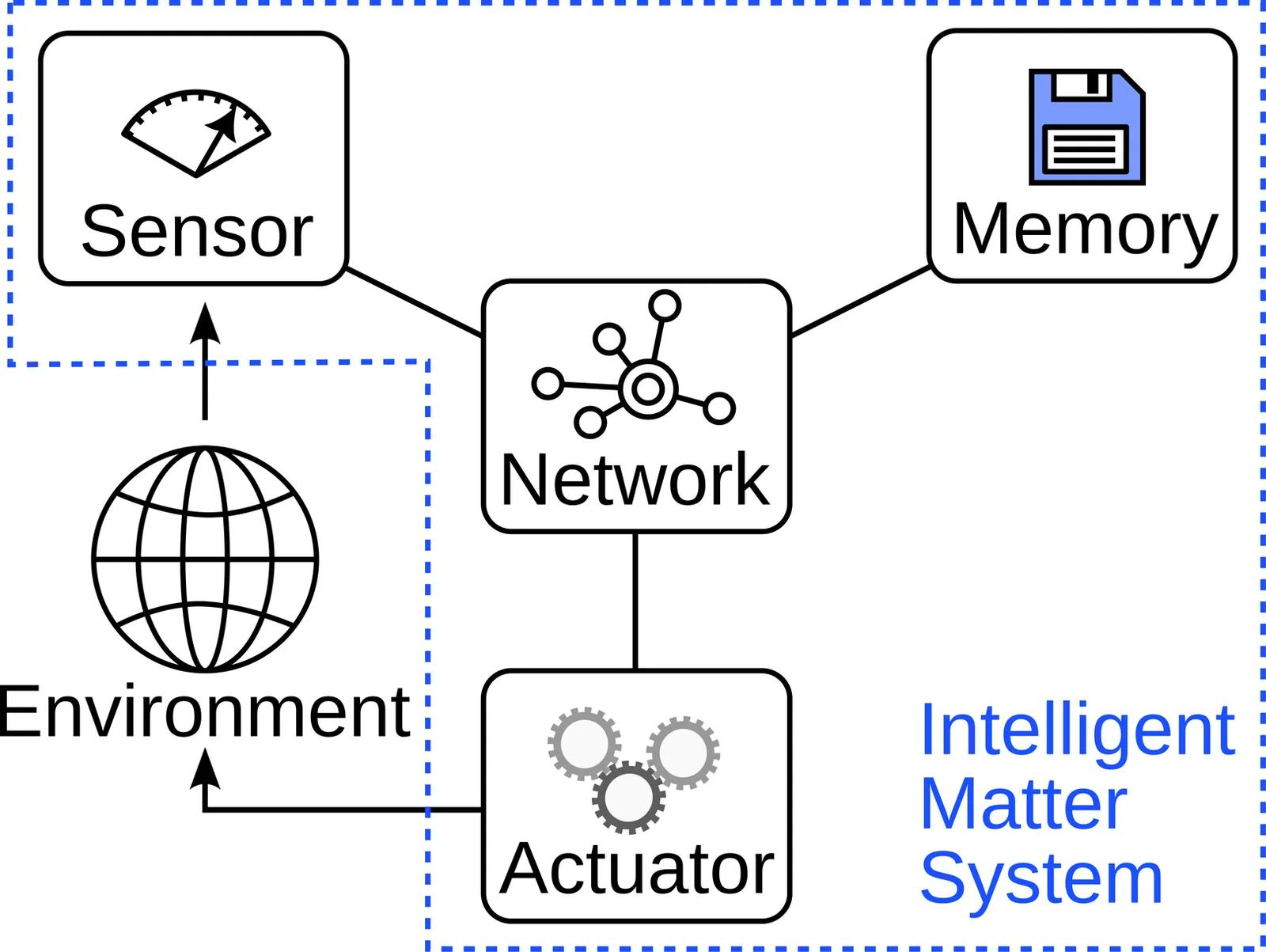
In this book chapter, we review how systems of simple motile agents can be used as a pathway to intelligent systems. It is a well known result from nature that large groups of entities following simple rules, such as swarms of animals, can give rise to much more complex collective behavior in a display of emergence. This begs the question whether we can emulate this behavior in synthetic matter and drive it to a point where the collective behavior reaches the complexity level of intelligent systems. Here, we will use a formalized notion of "intelligent matter" and compare it to recent results in the field of active matter. First, we will explore the approach of emergent computing in which specialized active matter systems are designed to directly solve a given task through emergent behavior. This we will then contrast with the approach of physical reservoir computing powered by the dynamics of active particle systems. In this context, we will also describe a novel reservoir computing scheme for active particles driven ultrasonically or via light refraction.

2512.13912Dec 2025

View

Onsager's Real Cavity model near solid interfaces

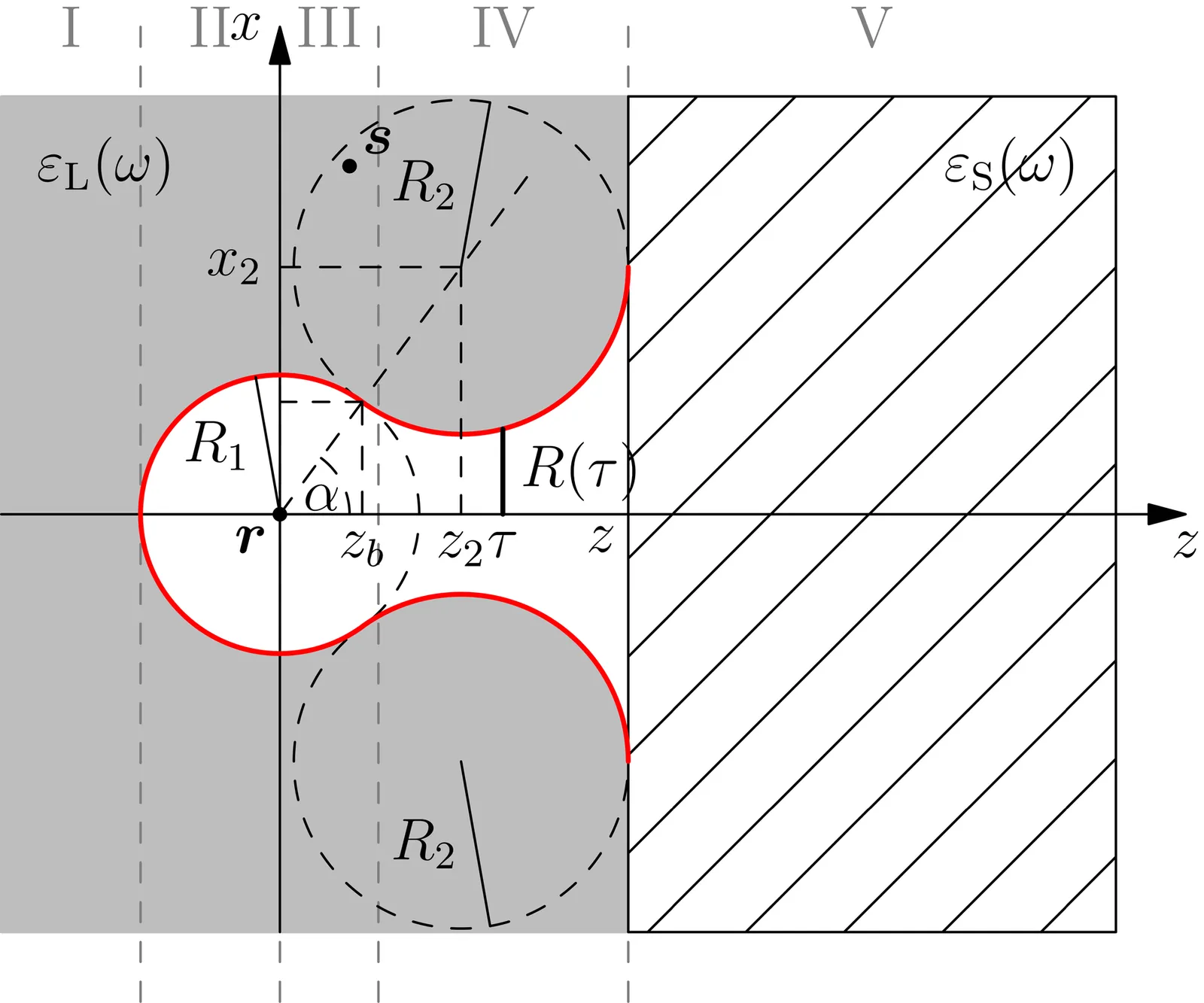
We develop an extended Onsager real-cavity framework to describe the Casimir-Polder interaction of small molecules dissolved in dielectric liquids near planar interfaces. By analytically resolving the geometry of the cavity opening, we derive a closed expression that arises when the molecule approaches a surface and connects them smoothly to the asymptotic medium-assisted interaction. Using experimentally established dielectric functions for water, propanol, and PTFE together with accurate molecular polarisabilities for O2 and N2, we compute the full distance-dependent potential for four molecule (O2 and N2)-liquid (water and propanol)-surface (PTFE) combinations. The results reveal how local-field screening inside the cavity, molecular polarisability, and liquid permittivity jointly determine the magnitude and shape of the interaction, including the characteristic transition from the open cavity (small separations) and closed cavity (large separations). The framework provides a transparent baseline for dispersion forces in liquids, while highlighting limitations associated with the point-dipole description, the absence of repulsive contributions, and the breakdown of the dipole approximation at ultrashort separations.

2512.19714Dec 2025

View

Elastocapillary adhesion of soft gel microspheres

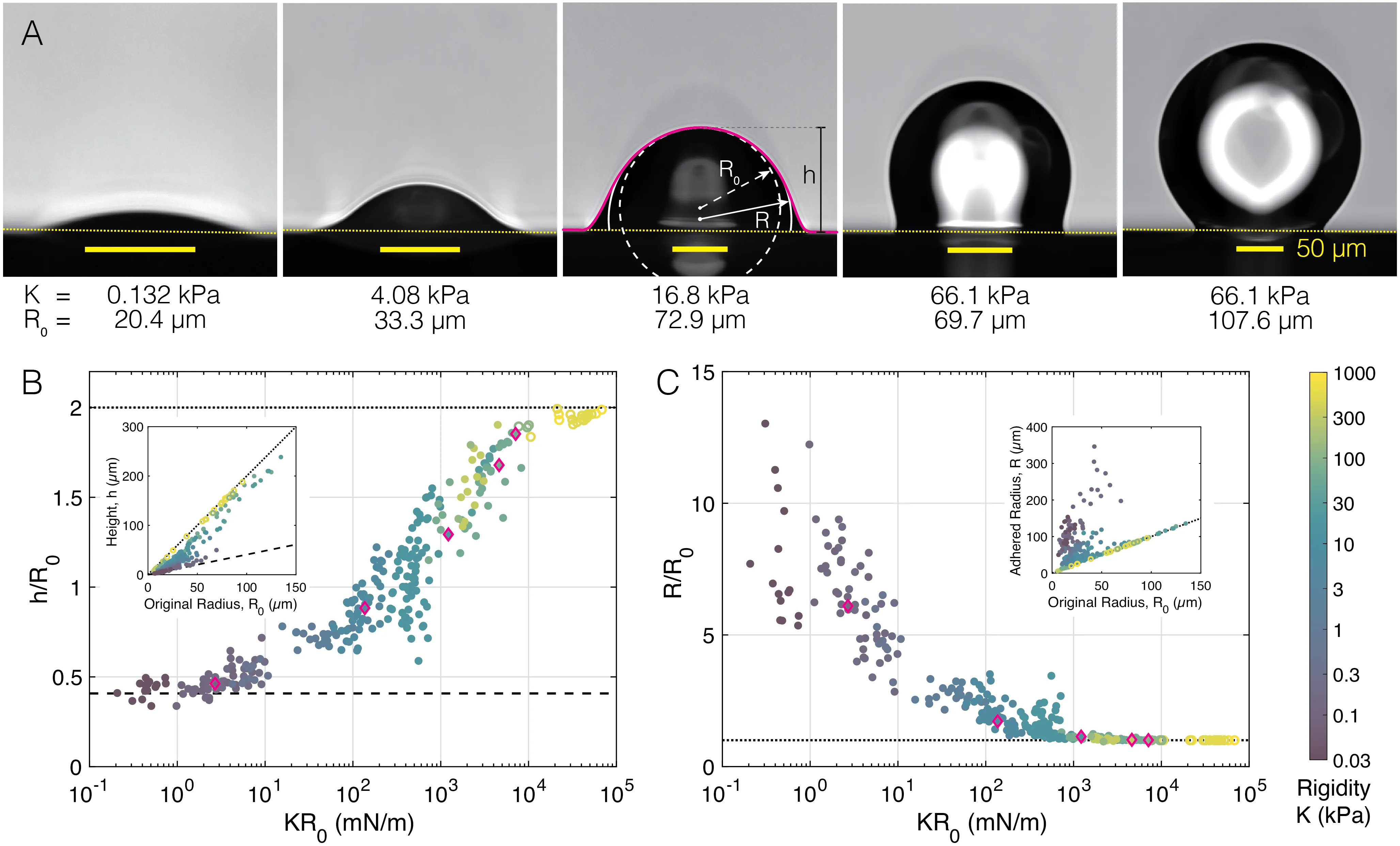
Softer means stickier for solid adhesives, because material compliance facilitates close contact between non-conformal surfaces. Recent discoveries have revealed that soft materials can exhibit a rich array of new physics arising from competing effects of continuum elasticity, fluid-like surface mechanics, and internal poroelastic flows, all of which can directly impact interfacial interactions. In this work, we investigate this complex interplay across several orders of magnitude of elastic stiffness by measuring the complete adhesive contact geometry between compliant silicone gel microspheres and flat, rigid substrates. We observe a continuous elastocapillary transition in adhesion mechanics, with novel features revealed by both the breadth of data and the detailed contact geometries. Importantly, soft gel spheres exhibit a remarkably broad range of near-equilibrium contact morphologies and their contact line deformation is always mediated by a fluid contact zone that phase separates from the gel. To explain this, we develop a new model incorporating elastocapillary and poroelastic mechanics that predicts the complete range of adhesive behavior and elucidates energetic tradeoffs. The data and model together reveal a shallow energy landscape that may contribute to the robustness of everyday adhesives.

2512.11752Dec 2025

View

Heat capacity of dense liquids: A link between two-phase model and melting temperature scaling

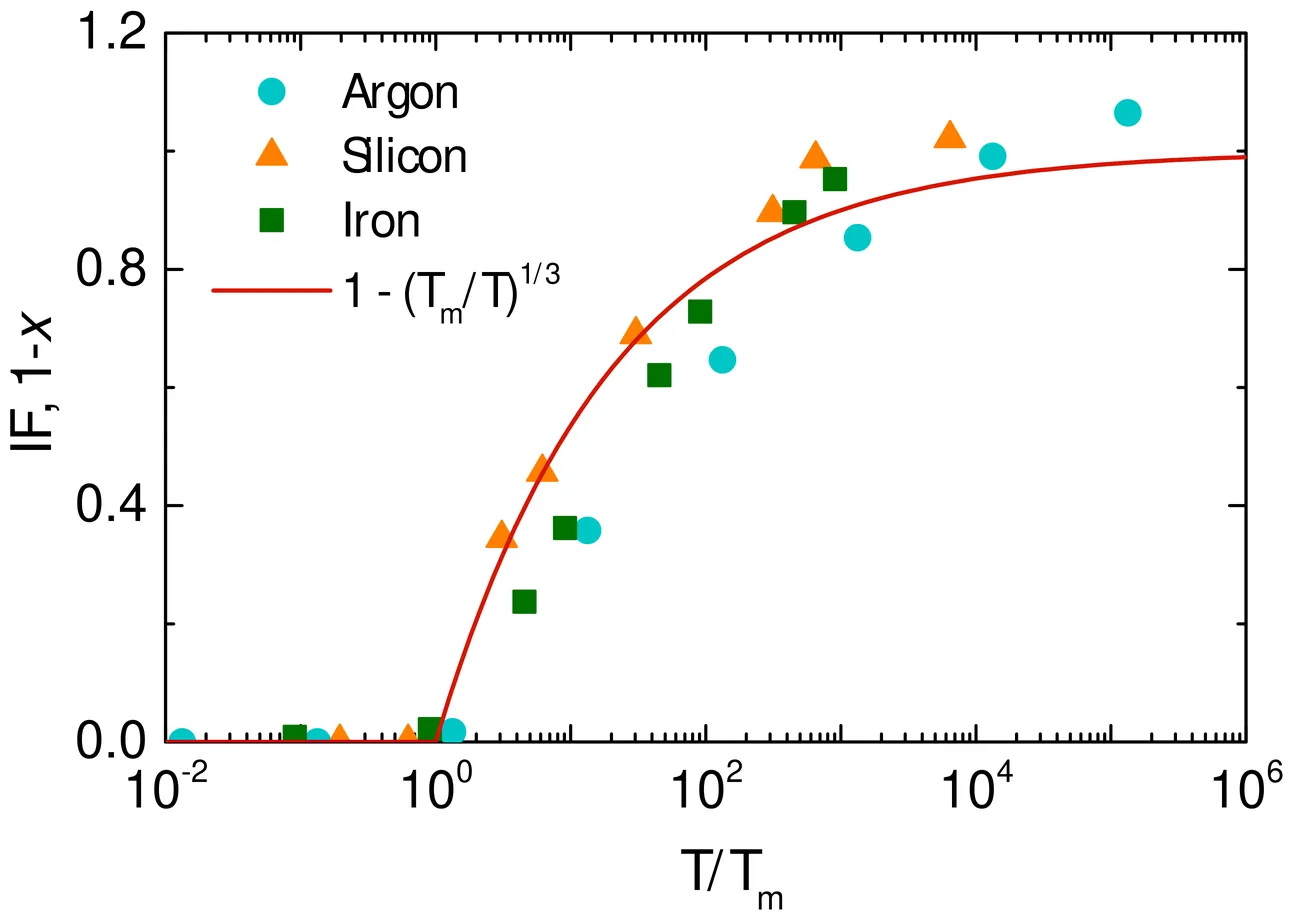
Generalized Rosenfeld-Tarazona scaling predicts the power-law dependence of the excess heat capacity of simple liquids on temperature. The two-phase model treats a liquid as a superposition of gas- and solid-like components whose relative abundance is quantified by a liquid rigidity parameter. We demonstrate here that the generalized Rosenfeld-Tarazona scaling emerges naturally in the two-phase model from the scale invariance of the liquid rigidity parameter.

2512.115203Dec 2025

View

Hydrodynamic permeability of fluctuating porous membranes

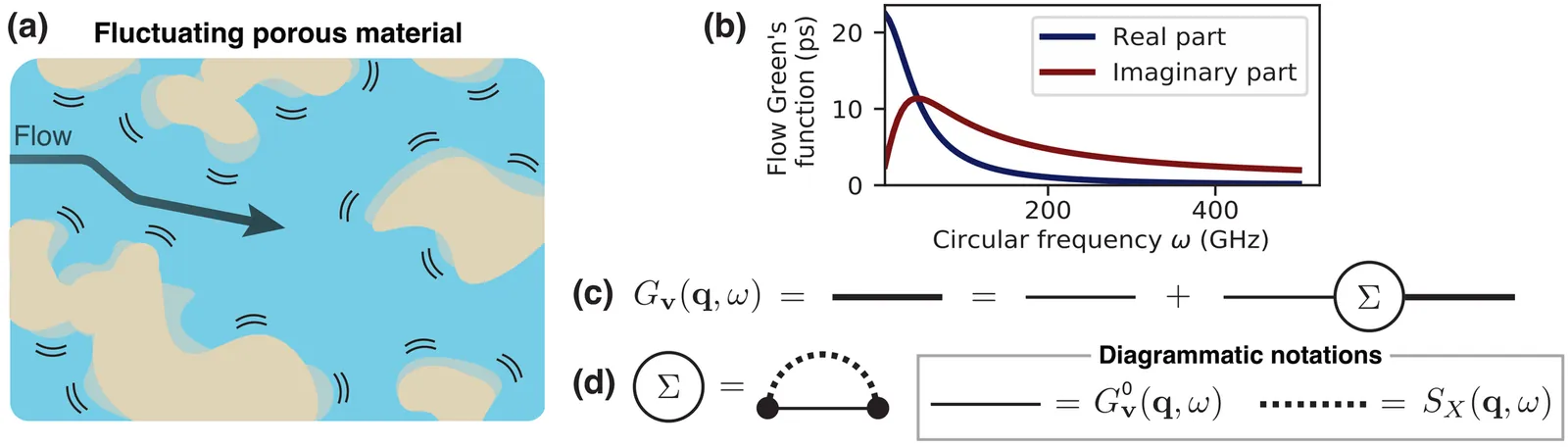
In this paper we examine how porosity fluctuations affect the hydrodynamic permeability of a porous matrix or membrane. We introduce a fluctuating Darcy model, which couples the Navier-Stokes equation to the space- and time-dependent porosity fluctuations via a Darcy friction term. Using a perturbative approach, a Dyson equation for hydrodynamic fluctuations is derived and solved to express the permeability in terms of the matrix fluctuation spectrum. Surprisingly, the model reveals strong modifications of the fluid permeability in fluctuating matrices compared to static ones. Applications to various matrix excitation models - breathing matrix, phonons, active forcing - highlight the significant influence of matrix fluctuations on fluid transport, offering insights for optimizing membrane design for separation applications.

2512.11368Dec 2025

View

Shear-induced pressure anisotropy in granular materials of nonspherical particles

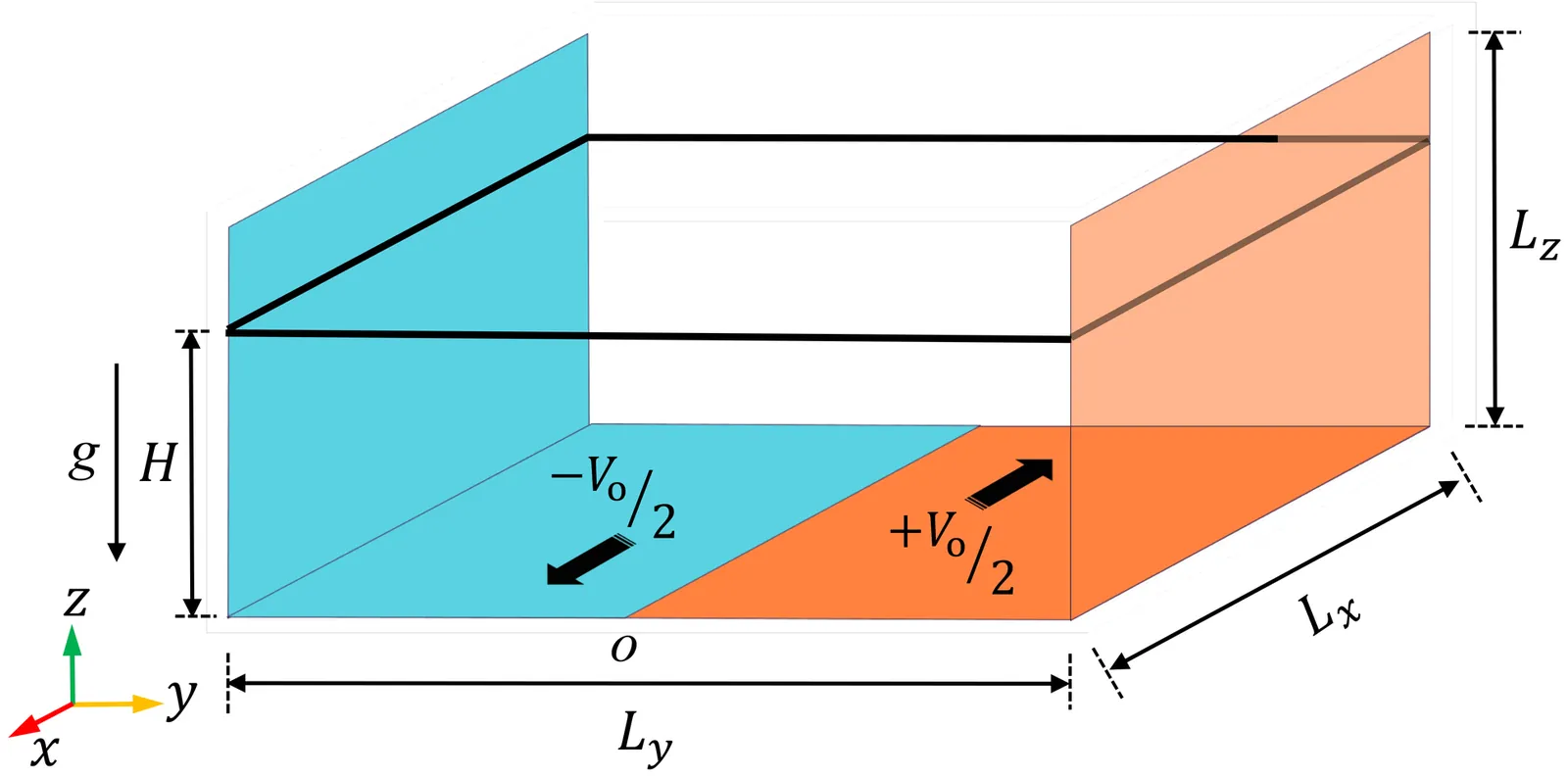
When a granular material composed of elongated grains is sheared in a split-bottom shear cell, a pressure difference develops within the material. This pressure difference depends on the interparticle friction ($μ$), which affects shear localization and particle alignment. For large $μ$, alignment is confined to a narrow shear band, leading to localized increases in packing density and pressure. For small $μ$, particles align over a wider region, leading to a nearly uniform packing density and pressure throughout the material. In contrast, spherical particles, regardless of $μ$, maintain a uniform packing density and pressure throughout the material. We observe a phenomenological similarity to the Weissenberg effect in non-Newtonian fluids, where normal stress differences induce radial pressure gradients, unlike the uniform pressure in Newtonian fluids.

2512.11157Dec 2025

View

2512.11123

Heterogeneity-Induced Oscillations in Active Nematics

One of the defining features of active nematics is that above a critical activity the quiescent state becomes unstable to a distorted, flowing one. We show that spatial variations in activity can fundamentally change the nature of this instability, affecting the symmetry of the unstable mode and producing spontaneous oscillations. We analytically identify a dynamical system for the evolution of the odd and even director modes, with the leading-order coefficients dependent on the activity profile, allowing a quantitative connection between the spatially-heterogeneous activity and dynamics, which we verify numerically. In the context of constant gradients in activity, we determine a phase diagram for the active response and highlight how variation of the activity profile causes the oscillations to vary from almost harmonic to relaxational. Our results indicate a novel route to spatio-temporal structure in active nematics and suggest experiments on controllable light-activated systems.

2512.11123Dec 2025

View

Curved Odd Elasticity

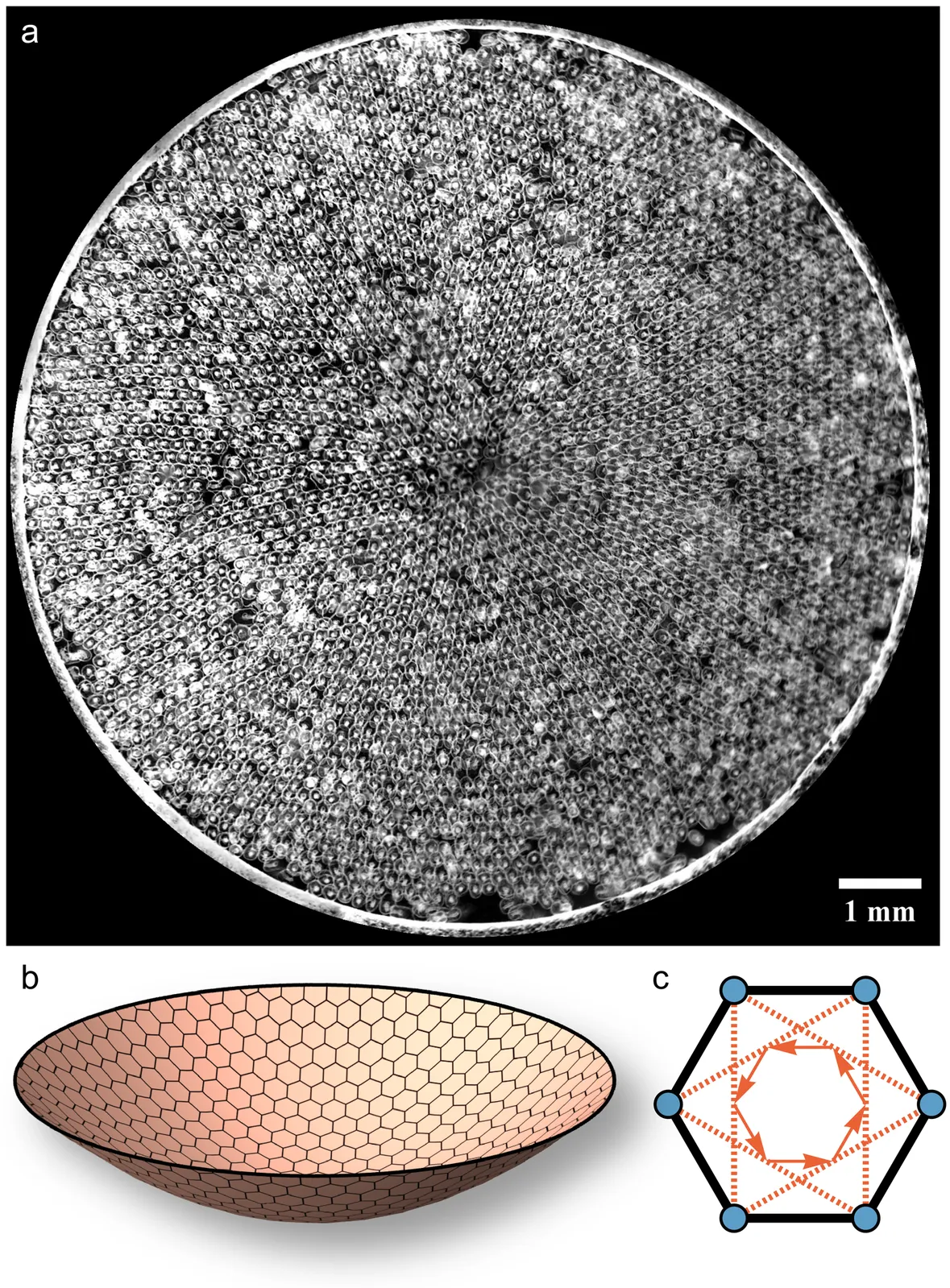
Living materials such as membranes, cytoskeletal assemblies, cell collectives and tissues can often be described as active solids -- materials that are energized from within, with elastic response about a well defined reference configuration. These materials often live in complex and curved manifolds, yet most descriptions of active solids are flat. Here, we explore the interplay between curvature and non-reciprocal elasticity via a covariant effective theory on curved manifolds in combination with numerical simulations. We find that curvature spatially patterns activity, gaps the spectrum, modifies exceptional points and introduces non-Hermitian defect modes. Together these results establish a foundation for hydrodynamic and rheological models on curved manifolds, with direct implications for living matter and active metamaterials.

2512.11037Dec 2025

View

Modeling Complex Multiphysics Systems with Discrete Element Method Enriched with the Kernel-Independent Fast Multipole Method

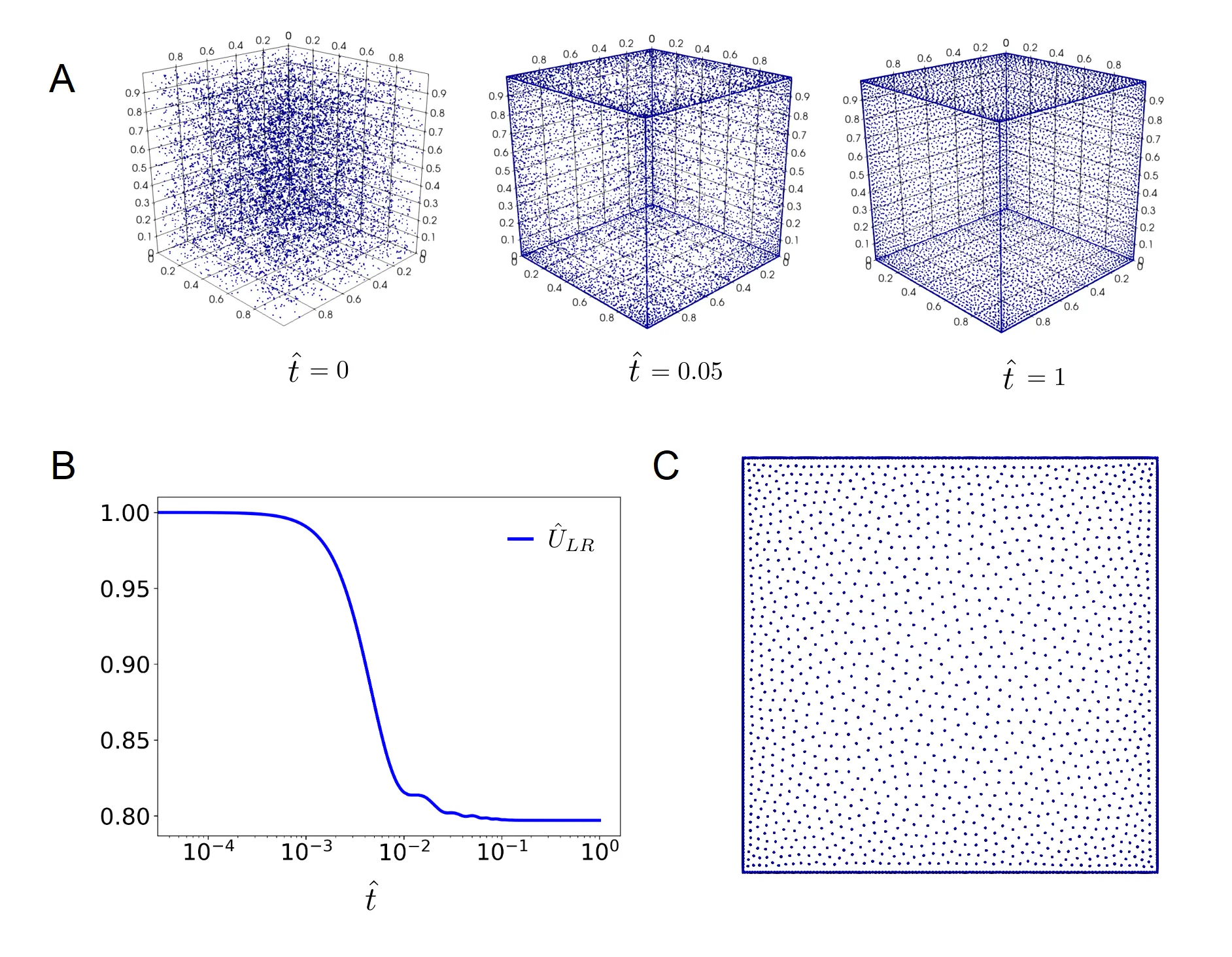
The paper describes the coupling of the MercuryDPM discrete element method (DEM) code and the implementation of the kernel-independent fast multipole method (KIFMM). The combined simulation framework allows addressing the large class of multiscale problems, including both the mechanical interactions of particulates at the fine scale and the long-range interactions of various natures at the coarse scale. Among these are electrostatic interactions in powders, clays, and particulates, magnetic interactions in ferromagnetic granulates, and gravitational interactions in asteroid clouds. The formalism of rigid clumps is successfully combined with KIFMM, enabling addressing problems involving complex long-large interactions between non-spherical particles with arbitrary charge distributions. The capabilities of our technique are demonstrated in several application examples.

2512.09478Dec 2025

View

Calibration of a DEM contact model for wet industrial granular materials

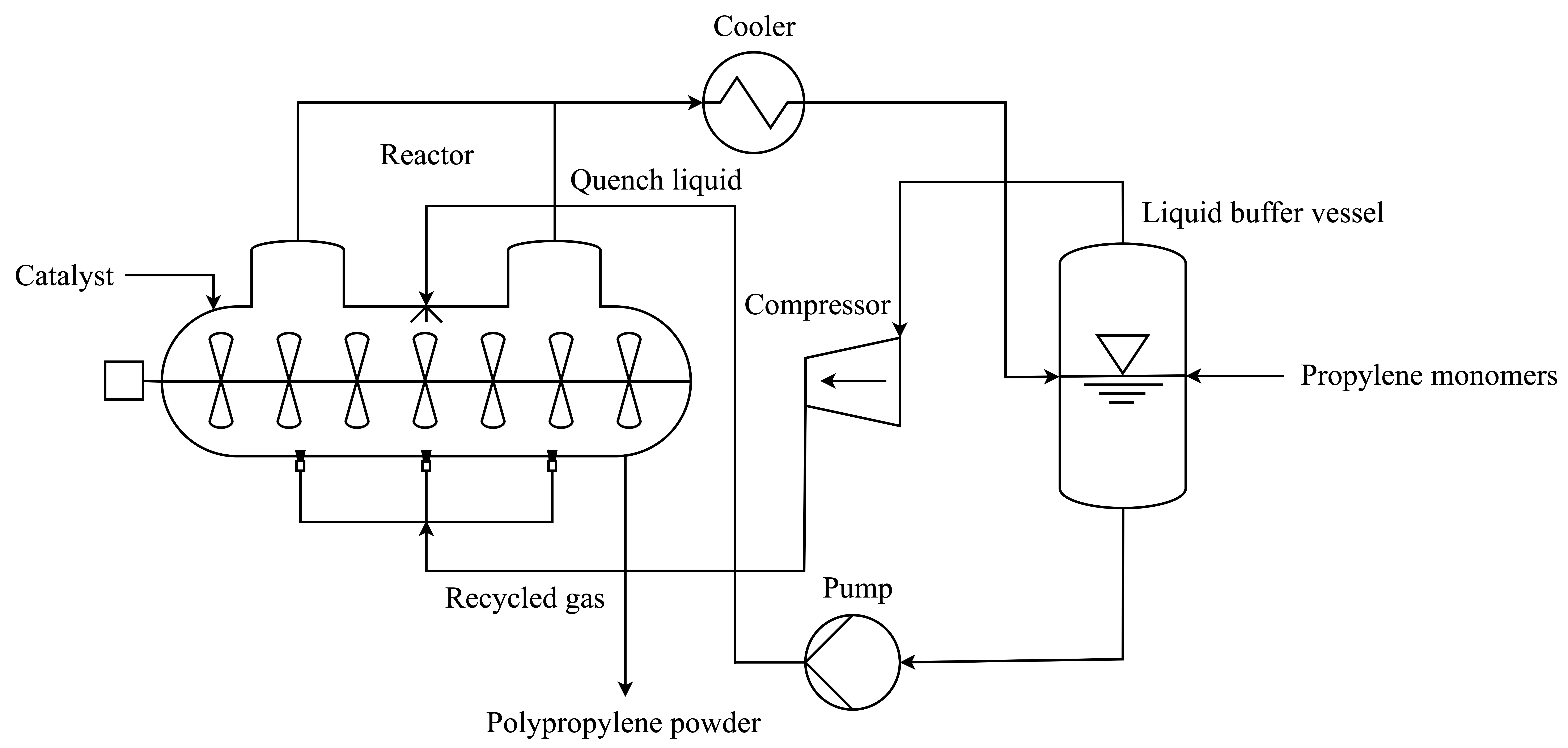
This study presents and calibrates a Discrete Element Method (DEM) contact model for wet granular materials in the pendular regime. The model extends a previously calibrated dry contact formulation by incorporating liquid bridges that generate capillary adhesion between particles, while liquid migration is represented through evolving bridge volumes. Two reactor-grade polypropylene powders with different particle size distributions, bulk densities, and surface morphologies are investigated, resulting in distinct wetting behavior. A schematic framework is introduced to relate increasing liquid content to the transition from dry to wet contacts using two key parameters: the minimum liquid film volume and the maximum liquid bridge volume. These parameters are calibrated using dynamic angle of repose measurements from rotating drum experiments. The calibrated model reproduces the experimental flow behavior of both powders: full agreement is obtained for the coarser, more porous powder across all liquid contents, while for the finer, denser powder, agreement is achieved at low to moderate liquid contents. At higher liquid contents, discrepancies arise due to agglomeration effects amplified by particle scaling. These results demonstrate the effectiveness of the dynamic angle of repose as a calibration target and highlight the limitations of particle scaling for strongly cohesive wet granular systems. The proposed framework provides a practical basis for DEM-based modeling of wet powder flow in industrial processes.

2512.08685Dec 2025

View

Many interacting particles in solution. I. Screening-ranged expansions of electrostatic potential and energy

We present an analytical many-body formalism for systems of spherical particles carrying arbitrary free charge distributions and interacting in a polarizable electrolyte solution, that we model within the linearized Poisson--Boltzmann framework. Building on the detailed spectral analysis of the associated nonstandard Neumann--Poincaré-type operators developed in our companion study arXiv:2512.08684, we construct exact explicit expansions of the electrostatic potential and energy in ascending orders of Debye screening thereby obtaining systematic "screening-ranged" series for potentials and energies. These screening-ranged expansions provide a unified and tractable description of many-body electrostatics. We demonstrate the versatility of the approach by showing how it generalizes and improves upon both classical and modern methods, enabling rigorous treatment of heterogeneously charged systems (such as Janus particles) and accurate modeling of higher-order phenomena (such as asymmetric dielectric screening, opposite-charge repulsion, like-charge attraction) as well as yielding many-body generalizations to analytical explicit results previously known only in the two-body setting.

2512.084073Dec 2025

View

Page 1 of 19