Trending in Condensed Matter
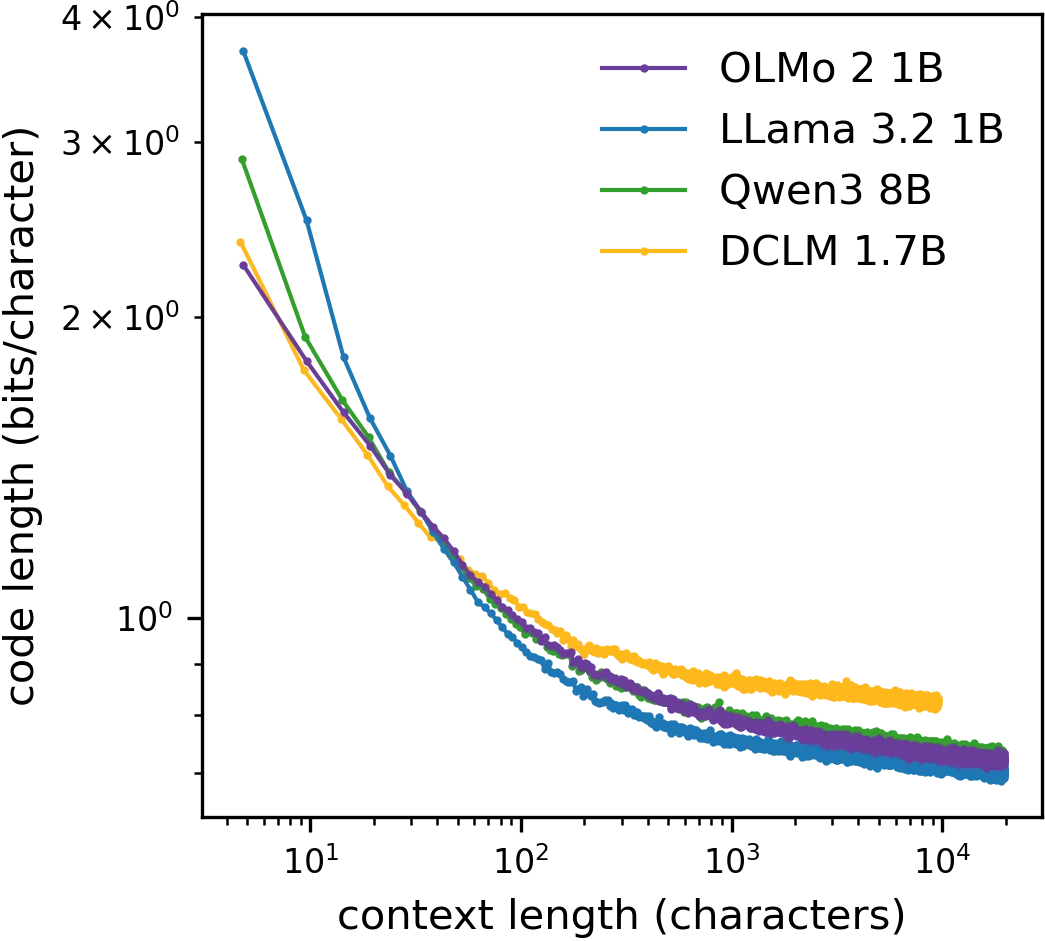
Large language models and the entropy of English
We use large language models (LLMs) to uncover long-ranged structure in English texts from a variety of sources. The conditional entropy or code length in many cases continues to decrease with context length at least to $N\sim 10^4$ characters, implying that there are direct dependencies or interactions across these distances. A corollary is that there are small but significant correlations between characters at these separations, as we show from the data independent of models. The distribution of code lengths reveals an emergent certainty about an increasing fraction of characters at large $N$. Over the course of model training, we observe different dynamics at long and short context lengths, suggesting that long-ranged structure is learned only gradually. Our results constrain efforts to build statistical physics models of LLMs or language itself.
2512.24969
Dec 2025Statistical Mechanics
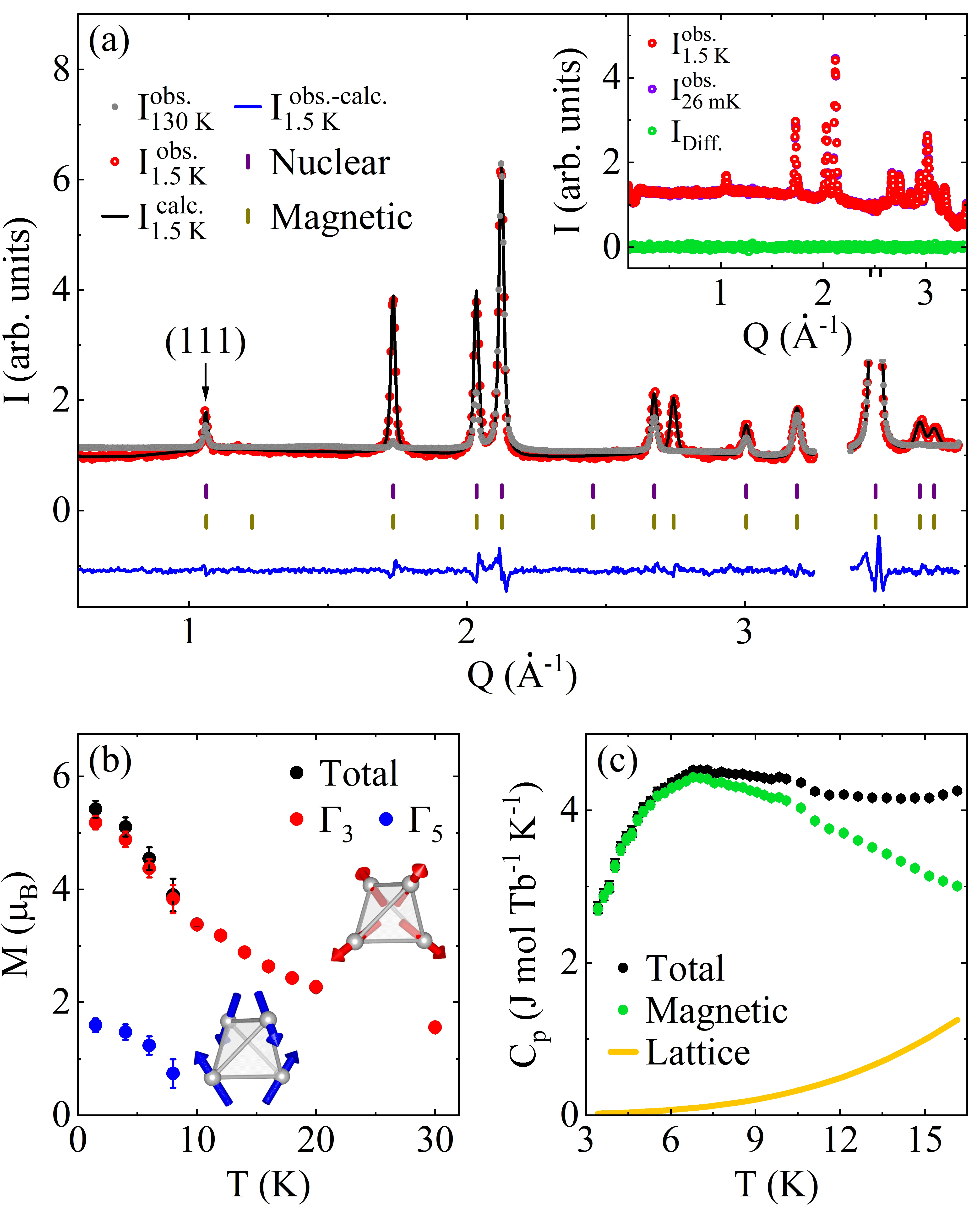
About the origin of the magnetic ground state of Tb$_{2}$Ir$_{2}$O$_{7}$
Magnetic-rare-earth pyrochlore iridates exhibit a rich variety of unconventional phases, driven by the complex interactions within and between the rare-earth and the iridium sublattices. In this study, we investigate the peculiar magnetic state of Tb$_{2}$Ir$_{2}$O$_{7}$, where a component of the Tb$^{3+}$ moment orders perpendicular to its local Ising anisotropy axis. By means of neutron diffraction and inelastic neutron scattering down to dilution temperatures, complemented by specific heat measurements, we show that this intriguing magnetic state is fully established at 1.5 K and we characterize its excitation spectrum across a broad range of energies. Our calculations reveal that bilinear interactions between Tb$^{3+}$ ions subjected to the Ir molecular field capture several key features of the experiments, but need to be supplemented to fully reproduce the observed behavior.
2601.00749
Jan 2026Strongly Correlated Electrons
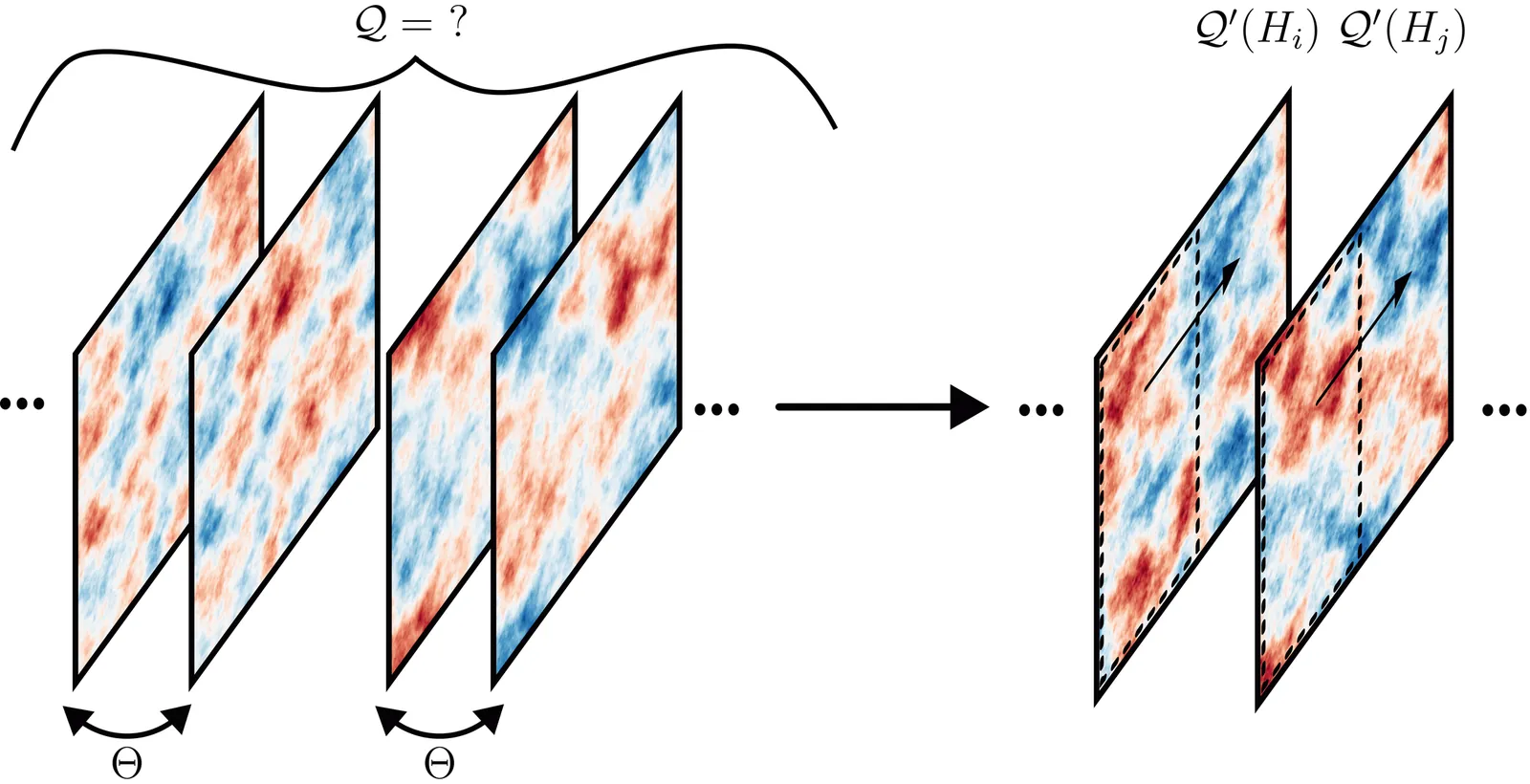
Symmetric approximant formalism for statistical topological matter
The standard approach to characterizing topological matter, computing topological invariants, fails when the symmetry protecting the topological phase is preserved only on average in a disordered system. Because topological invariants rely on enforcing the symmetry exactly, they can overcount phases by incorrectly identifying certain non-robust features as robust. Moreover, in intrinsic statistical topological insulators, enforcing the symmetry exactly is guaranteed to destroy the topological phase. We define a mapping that addresses both issues and provides a unified framework for describing disordered topological matter.
2601.00784
Jan 2026Mesoscale and Nanoscale Physics
 2601.00294
2601.00294Bridging Commutant and Polynomial Methods for Hilbert Space Fragmentation
A quantum model exhibits Hilbert space fragmentation (HSF) if its Hilbert space decomposes into exponentially many dynamically disconnected subspaces, known as Krylov subspaces. A model may however have different HSFs depending on the method for identifying them. Here we establish a connection between two vastly distinct methods recently proposed for identifying HSF: the commutant algebra (CA) method and integer characteristic polynomial factorization (ICPF) method. For a Hamiltonian consisting of operators admitting rational number matrix representations, we prove a theorem that, if its center of commutant algebra have all eigenvalues being rational, the HSF from the ICPF method must be equal to or finer than that from the CA method. We show that this condition is satisfied by most known models exhibiting HSF, for which we demonstrate the validity of our theorem. We further discuss representative models for which ICPF and CA methods yield different HSFs. Our results may facilitate the exploration of a unified definition of HSF.
2601.00294
Jan 2026Statistical Mechanics
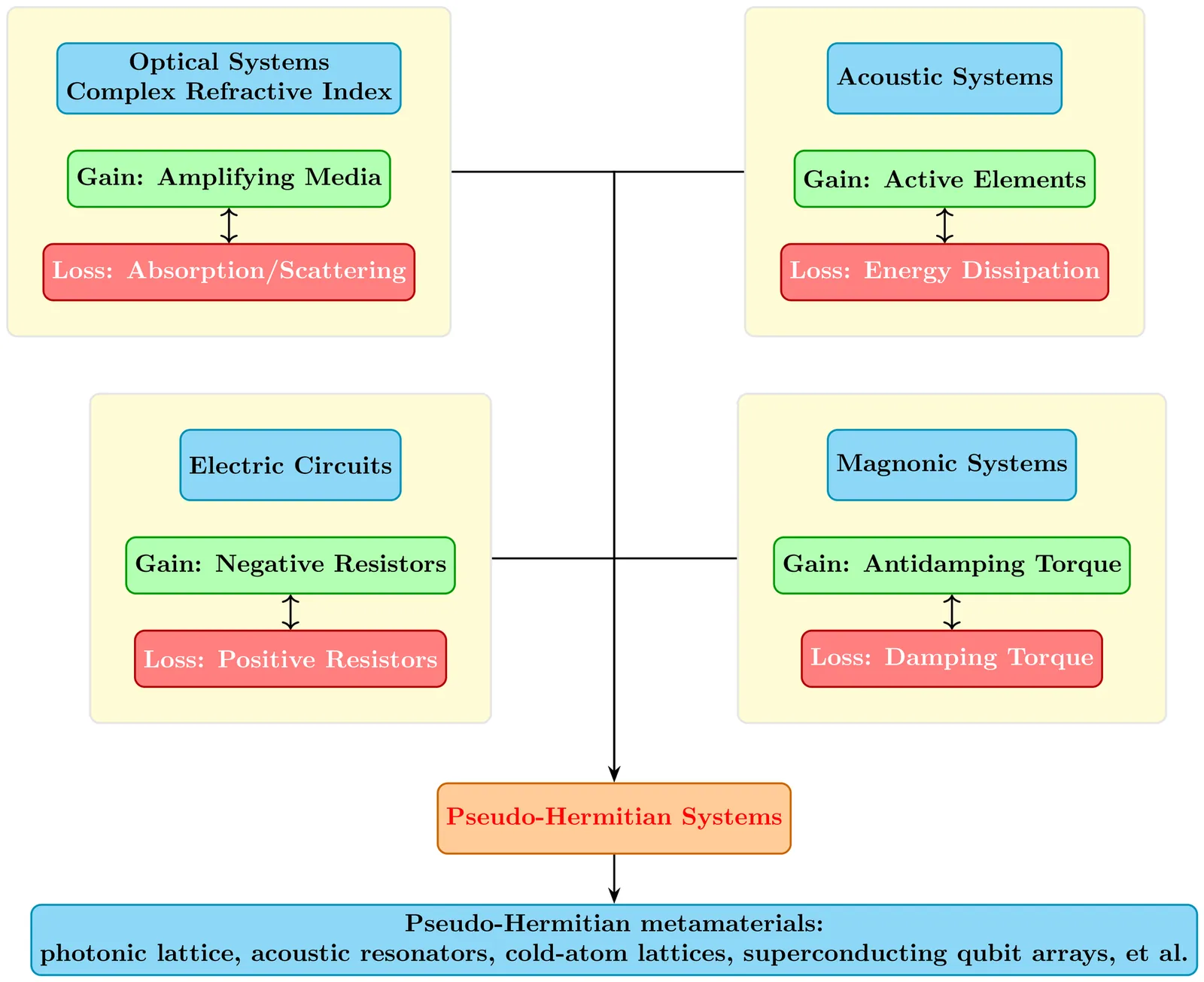
Pseudo-Hermitian Magnon Dynamics
A defining quantity of a physical system is its energy which is represented by the Hamiltonian. In closed quantum mechanical or/and coherent wave-based systems the Hamiltonian is introduced as a Hermitian operator which ensures real energy spectrum and secures the decomposition of any state over a complete basis set spanning the space where the states live. Pseudo-Hermitian, or PT symmetric, systems are a special class of non-Hermitian ones. They describe open systems but may still have real energy spectrum. The eigenmodes are however not orthogonal in general. This qualitative difference to Hermitian physics has a range of consequences for the physical behaviour of the system in the steady state or when it is subjected to external perturbations. This overview reviews the recent progress in the field of pseudo-Hermitian physics as it unfolds when applied to low-energy excitations of magnetically ordered materials. The focus is mainly on long wave length spin excitations (spin waves) with magnons being the energy quanta of these excitations. Various setups including ferromagnetic, antiferromagnetic, magnonic crystals, and hybride structures with different types of coupling to the environments as well as spatio-temporally engineered systems will be discussed with a focus on the particular aspects that are brought about by the pseudo-Hermiticity such as mode amplifications, non-reciprocal propagation, magnon cloaking, non-Hermitian skin effect, PT-symmetric assisted Floquet engineering, topological energy transfer, and field-induced enhanced sensitivity.
2601.00701
Jan 2026Mesoscale and Nanoscale Physics
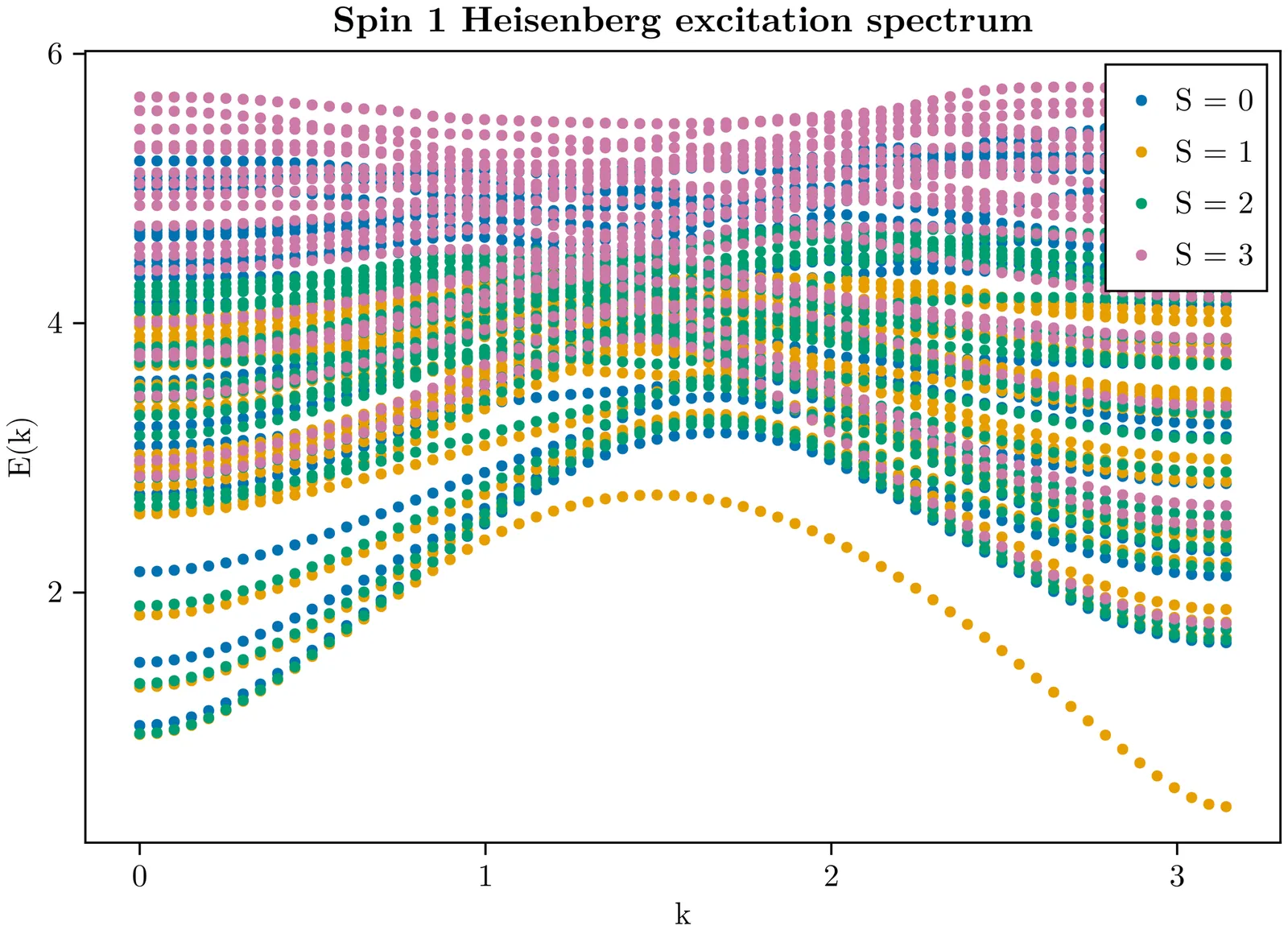
Les Houches Lectures Notes on Tensor Networks
Tensor networks provide a powerful new framework for classifying and simulating correlated and topological phases of quantum matter. Their central premise is that strongly correlated matter can only be understood by studying the underlying entanglement structure and its associated (generalised) symmetries. In essence, tensor networks provide a compressed, holographic description of the complicated vacuum fluctuations in strongly correlated systems, and as such they break down the infamous many-body exponential wall. These lecture notes provide a concise overview of the most important conceptual, computational and mathematical aspects of this theory.
2512.24390
Dec 2025Strongly Correlated Electrons
Lectures on insulating and conducting quantum spin liquids
Two of the iconic phases of the hole-doped cuprate materials are the intermediate temperature pseudogap metal and the lower temperature $d$-wave superconductor. Following the prescient suggestion of P.W. Anderson, there were numerous early theories of these phases as doped quantum spin liquids. However, these theories have had difficulties with two prominent observations: (i) angle-dependent magnetoresistance measurements (ADMR), including observation of the Yamaji effect, present convincing evidence of small hole pockets which can tunnel coherently between square lattice layers, and (ii) the velocities of the nodal Bogoliubov quasiparticles in the $d$-wave superconductor are highly anisotropic, with $v_F \gg v_Δ$. These lecture notes review how the fractionalized Fermi Liquid (FL*) state, which dopes quantum spin liquids with gauge-neutral electron-like quasiparticles, resolves both difficulties. Theories of insulating quantum spin liquids employing fractionalization of the electron spin into bosonic or fermionic partons are discussed. Doping the bosonic parton theory leads to a holon metal theory: while not appropriate for the cuprate pseudogap, this theory is argued to apply to the Lieb lattice. Doping the fermionic parton theory leads to a $d$-wave superconductor with nearly isotropic quasiparticle velocities. The construction of the FL* state is described using a quantum dimer model, followed by a more realistic description using the Ancilla Layer Model (ALM), which is then used to obtain the theory of the pseudogap and the $d$-wave superconductor.
2512.23962
Dec 2025Strongly Correlated Electrons
Emergence of 3D Superconformal Ising Criticality on the Fuzzy Sphere
Supersymmetric conformal field theories (SCFTs) form a unique subset of quantum field theories which provide powerful insights into strongly coupled critical phenomena. Here, we present a microscopic and non-perturbative realization of the three-dimensional $\mathcal{N}=1$ superconformal Ising critical point, based on a Yukawa-type coupling between a 3D Ising CFT and a gauged Majorana fermion. Using the recently developed fuzzy sphere regularization, we directly extract the scaling dimensions of low-lying operators via the state-operator correspondence. At the critical point, we demonstrate conformal multiplet structure together with the hallmark of emergent spacetime supersymmetry through characteristic relations between fermionic and bosonic operators. Moreover, by tuning the Yukawa coupling, we explicitly track the evolution of operator spectra from the decoupled Ising-Majorana fixed point to the interacting superconformal fixed point, revealing renormalization-group flow at the operator level. Our results establish a controlled, non-perturbative microscopic route to 3D SCFTs.
2512.25054
Dec 2025Strongly Correlated Electrons
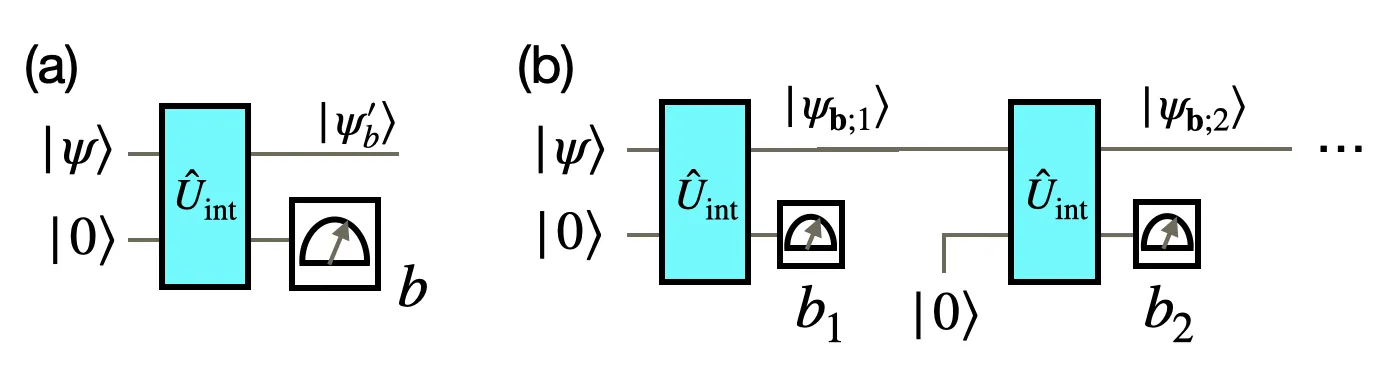
An introduction to monitored quantum systems and quantum trajectories: spectrum, typicality, and phases
Thanks to recent experimental advances in simulating and detecting quantum dynamics with high precision and controllability, our understanding of the physics of monitored quantum systems has considerably deepened over the past decades. In this article, we provide an introductory theoretical review on the basic formalisms governing open quantum dynamics under measurement, along with recent developments in their spectral and typical aspects. After reviewing quantum measurement theory, we introduce the concept of quantum trajectories, which are the conditional dynamics of monitored states shaped by a set of measurement outcomes. We then discuss the spectral properties of the dynamical map describing the evolution averaged over measurement outcomes. As has recently been recognized, these spectral features are intimately connected to whether quantum trajectories exhibit typical behaviors, such as the ergodicity and purification. Moreover, we introduce Lyapunov exponents of typical quantum trajectories and discuss how these quantities serve as indicators of measurement-induced phase transitions in monitored quantum many-body systems.
2512.19922
Dec 2025Statistical Mechanics
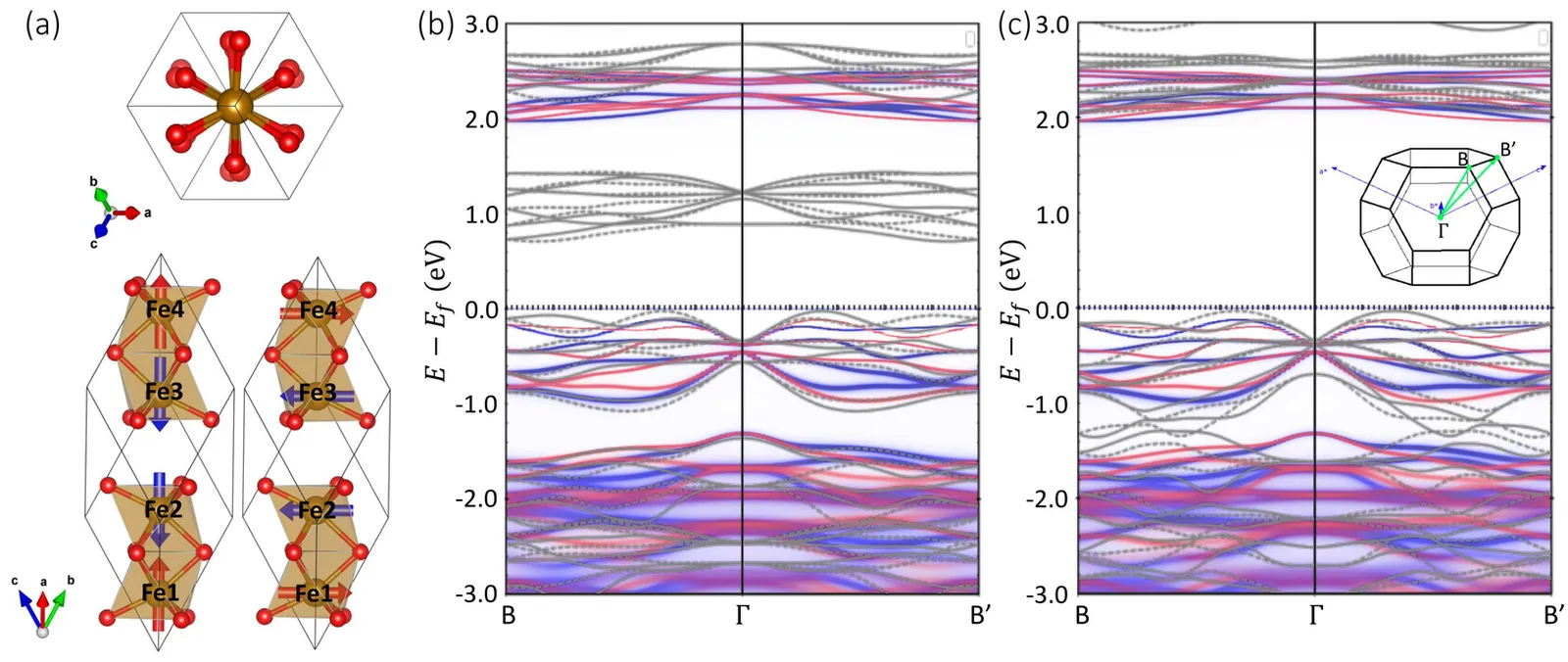
X-ray magnetic circular dichroism of altermagnet $α$-Fe$_2$O$_3$ based on multiplet ligand-field theory using Wannier orbitals
Hematite $α$-Fe$_2$O$_3$ is a $g$-wave altermagnetic material, which has an easy-axis phase and easy-plane weak ferromagnetic phase below and above Morin transition temperature, respectively. The presence of these phases renders it a good candidate to study the characteristic spin splitting in altermagnets under the impacts of relativistic effect and finite temperature. In this regard, we have calculated the band structure of $α$-Fe$_2$O$_3$ based on density functional theory (DFT) which also considers the Hubbard-U correction and spin-orbit coupling (SOC) effects. Additionally, the charge self-consistent DFT + dynamical mean-field theory (DMFT) calculations have been performed at finite temperatures. It is found that the altermagnetic spin splitting in $α$-Fe$_2$O$_3$ preserves with either SOC or temperature effect taken into account. Furthermore, we present a numerical simulation of the x-ray magnetic circular dichroism (XMCD) of the L$_{2,3}$ edge of Fe using a combination of DFT with multiplet ligand-field theory (MLFT). In terms of the different Néel vectors present in $α$-Fe$_2$O$_3$, we calculate the x-ray absorption spectroscopy (XAS) of the L$_{2,3}$ edge of Fe in the form of conductivity tensor and analyze the XMCD response from a perspective of symmetry. A characteristic XMCD line shape is expected when the Néel vector is along [010] direction (magnetic point group $2^\prime/m^\prime$) and the light propagation vector is perpendicular to the Néel vector, which can be further distinguished from the XMCD response originated from weak ferromagnetism with the light propagation vector parallel to the Néel vector.
2512.11664
Dec 2025Materials Science
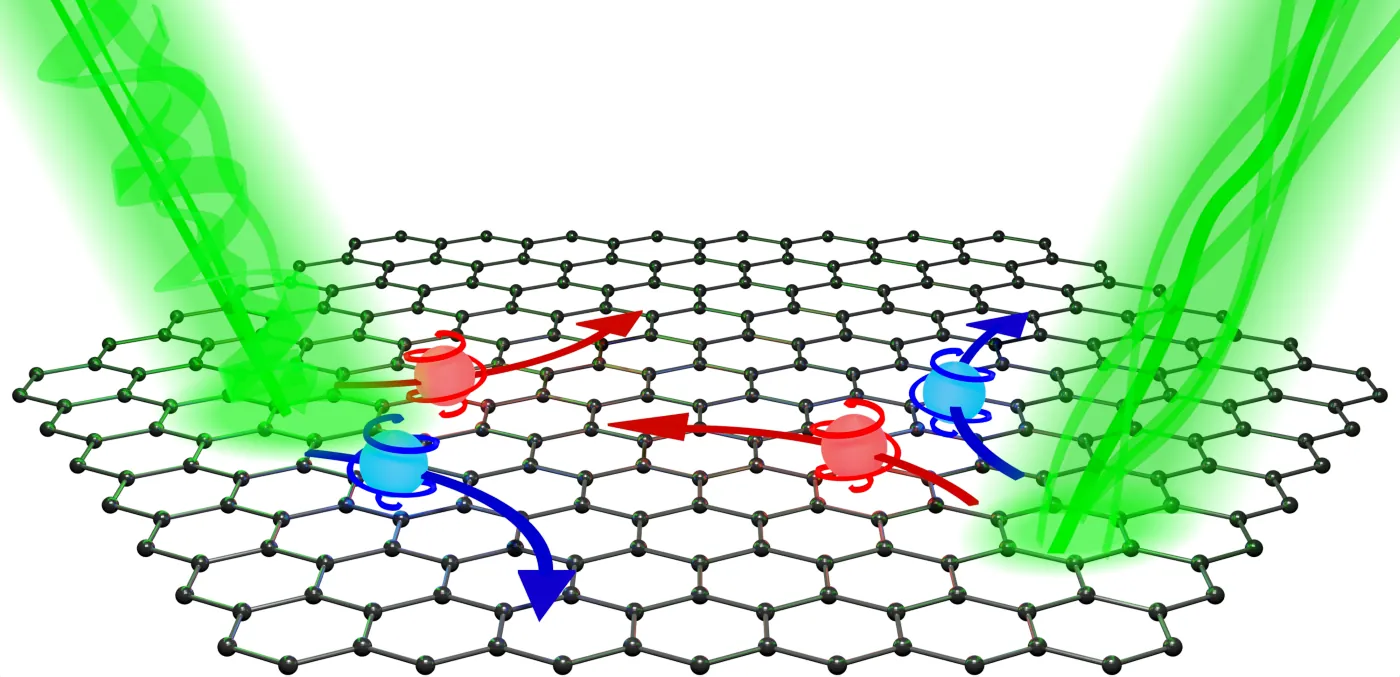
Electric and spin-valley currents induced by structured light in 2D Dirac materials
Structured optical fields can be used for the injection and control of charge and spin-valley currents. Here, we present a systematical study of these phenomena for interband absorption of structured light in 2D Dirac materials. We derive general expressions for the current density and the quasi-classical generation rate of photoelectrons in the momentum, coordinate, and spin-valley spaces. We reveal mechanisms of the current formation determined by the local and non-local contributions to the optical generation, including the mechanisms related to optical alignment of electron momenta by linearly polarized light, optical orientation by circularly polarized light, and the class of charge and spin-valley photon drags sensitive to the phase and polarization profiles of the optical field. We develop a kinetic theory of electric and spin-valley currents driven by the optical field with spatially inhomogeneous intensity, polarization, and phase and obtain analytical expressions for the current contributions. The theory is applied to analyze the photocurrents emerging in TMDC layers and graphene excited by polarization gratings.
2512.11677
Dec 2025Mesoscale and Nanoscale Physics
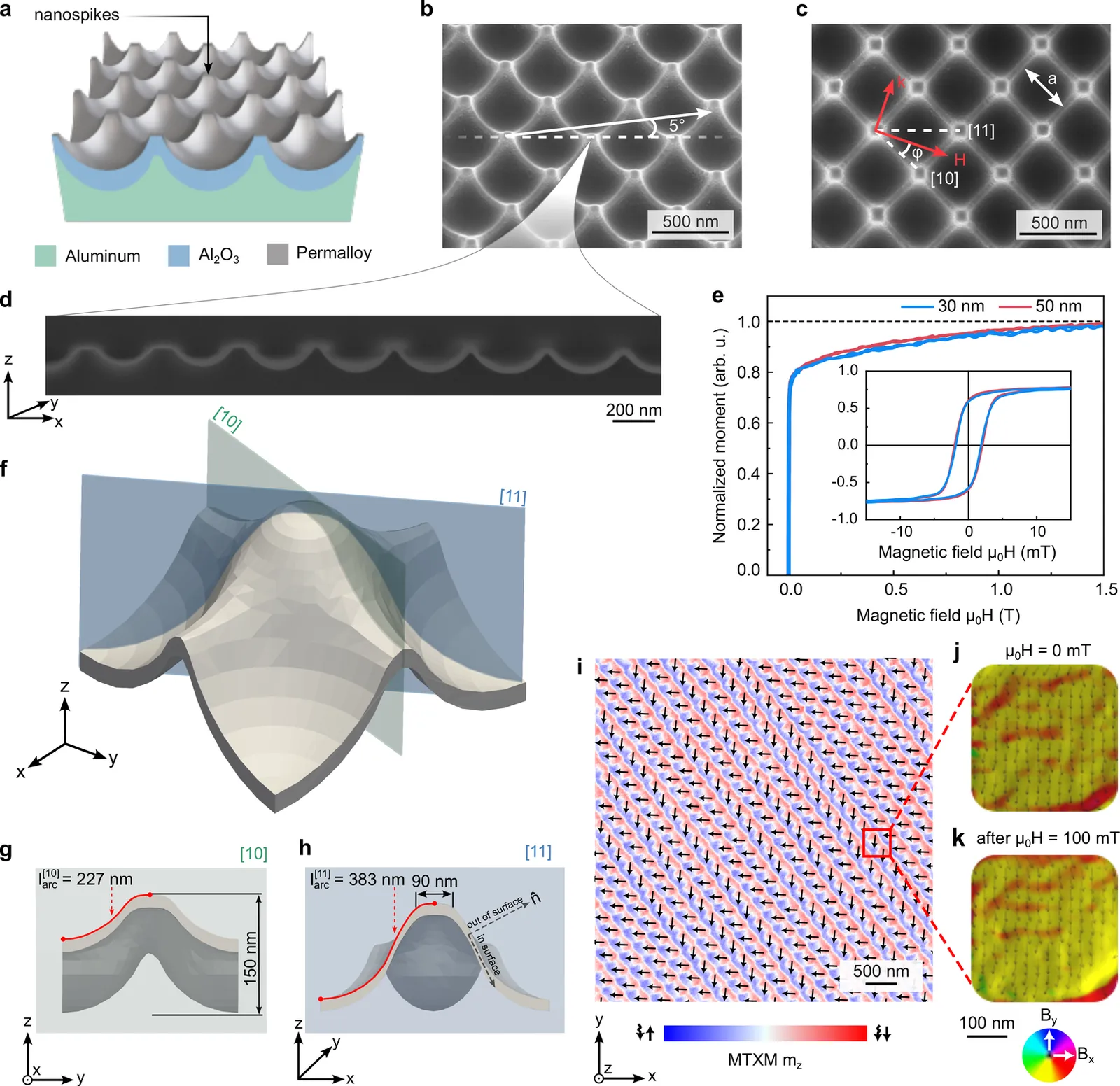
Curvilinear magnonic crystal based on 3D hierarchical nanotemplates
Curvilinear magnetic nanostructures enable control of magnetization dynamics through geometry-induced anisotropy and chiral interactions as well as magnetic field modulation. In this work, we report a curvilinear magnonic crystal based on large-area square arrays of truncated nanospikes fabricated by conformal coating of 3D hierarchical templates with permalloy thin films. Brillouin light scattering spectroscopy reveals anisotropic band structure with multiple dispersive and folded Bloch-type dispersive spin-wave modes as well as non-dispersive modes exhibiting direction-dependent frequency shifts and intensity asymmetries along lattice principal axes. Finite element micromagnetic simulations indicate that curvature-induced variations of the demagnetizing field govern the magnonic response, enabling the identification of modes propagating in nanochannels and other localized on nanospike apexes or along the ridges connecting adjacent nanospikes. The combination of geometric curvature and optical probing asymmetry produces directional dependence of magnonic bands, establishing 3D hierarchical templates as a versatile platform for curvature-engineered magnonics.
2512.11663
Dec 2025Strongly Correlated Electrons
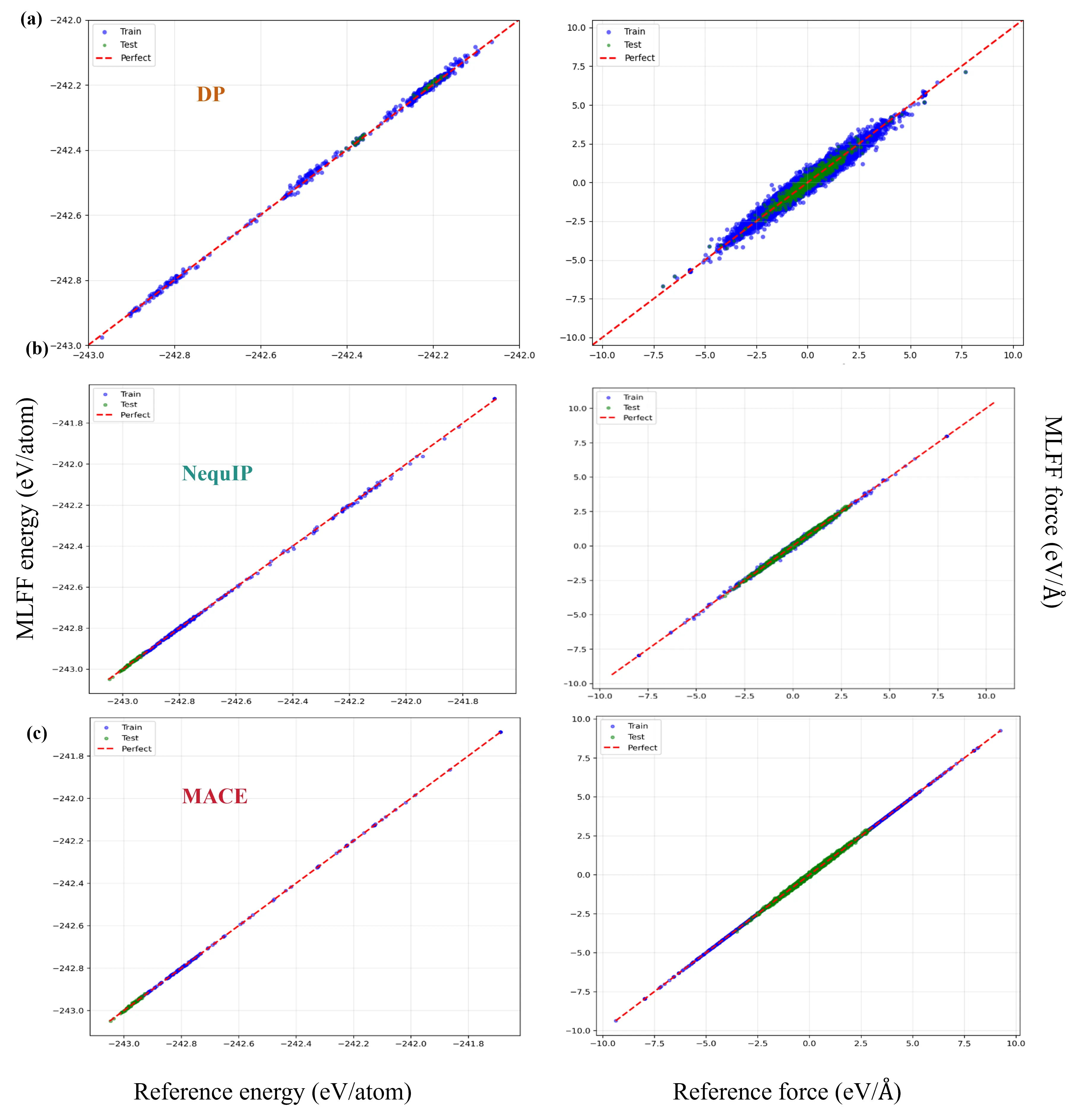
Influence of Exchange-Correlation Functionals and Neural Network Architectures on Li$^+$-Ion Conductivity in Solid-State Electrolyte from Molecular Dynamics Simulations with Machine-Learning Force Fields
With the rapid advancement of machine learning techniques for materials simulations, machine-learned force fields (MLFFs) have become a powerful tool that complements first-principles calculations by enabling high-accuracy molecular dynamics simulations over extended timescales. Typically, MLFFs are trained on data generated from density functional theory (DFT) using a specific exchange-correlation (XC) functional, with the goal of reproducing DFT-level properties. However, the uncertainties in MLFF-based simulations--arising from variations in both MLFF model architectures and the choice of XC functionals--remain insufficiently understood. In this work, we construct MLFF models of different architectures trained on DFT data from both semilocal and hybrid functionals to describe Li$^+$ diffusion in the solid-state electrolyte Li$_6$PS$_5$Cl. We systematically investigate how different XC functionals influence the Li$^+$ diffusion coefficient. To reduce statistical uncertainty, the mean squared displacements are averaged over 300 independent molecular dynamics (MD) trajectories of 70 ps each, yielding statistical variations below $1\%$. This enables a clear assessment of the respective influences of the functional and the MLFF model. Due to its tendency to underestimate band gaps and migration barriers, the semilocal functional predicts consistently higher Li$^+$ diffusion coefficients, compared to the hybrid functional. Furthermore, comparisons among various neural network methods reveal that the differences in predicted diffusion coefficients arising from different network architectures are of the same order of magnitude as those caused by different functionals, indicating that the choice of the network model itself substantially influences the MLFF predictions. This observation calls from an urgent need for standardized protocols to minimize model-dependent biases in MLFF-based MD.
2512.11650
Dec 2025Materials Science
 2512.03148
2512.03148Proof that Momentum Mixing Hatsugai Kohmoto equals the Twisted Hubbard Model
We prove formally that the momentum-mixing Hatsugai-Kohmoto model (MMHK) is the Hubbard model with a twist. With this result in tow, we rely on the proof of Watanabe's that two models which differ by a twist must have the same bulk physics. Consequently, we have proven that MMHK=Hubbard in the charge sector.
2512.03148
Dec 2025Strongly Correlated Electrons
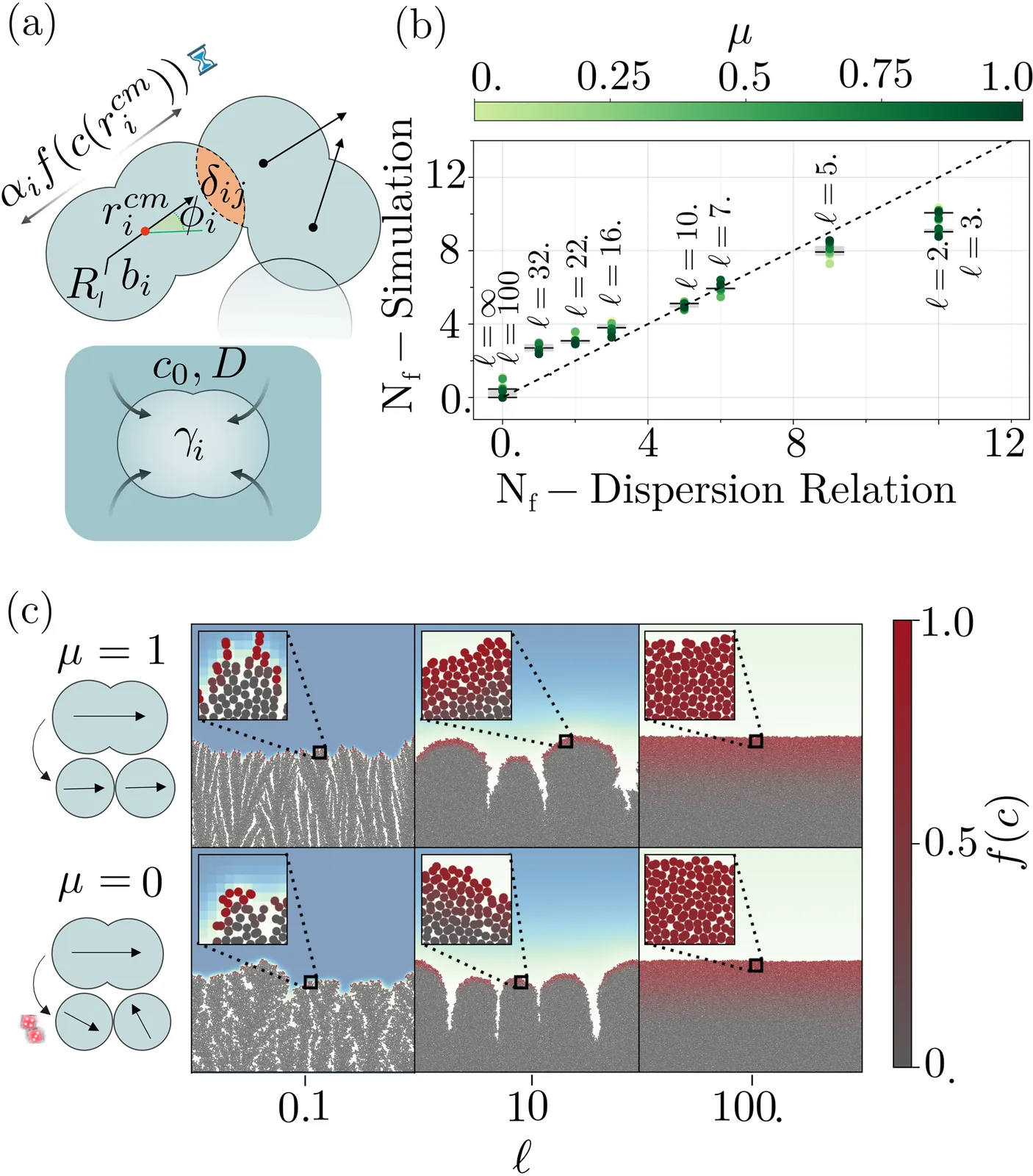
Orientational lineage memory and mechanical ordering during diffusion-limited growth
Growth and shape formation in crowded multicellular assemblies arise from the interplay of chemical gradients, single-cell expansion and mechanical interactions, making it essential to understand how these processes jointly shape collective organization. Using a particle-based model that resolves nutrient fields as well as cellular orientations and their inheritance, we investigate how orientational order emerges within expanding fronts whose morphology is set by nutrient limitation. We identify a transition in nematic order controlled by front morphology, with orientational memory influencing alignment only on one side of this transition. Under strong inheritance, orientational order varies non-monotonically: both thin active layers (fingering morphologies) and thick active layers (flat fronts) produce strong alignment, whereas intermediate cases are less ordered. Analysis of velocities, reorientation statistics, and stress anisotropies shows that this behavior reflects a shift from inheritance-dominated to mechanically driven alignment that overrides lineage memory. The resulting differences in front speed produce a fitness advantage of orientational memory only in the diffusion-limited, memory-dominated regime. These findings elucidate how nutrient supply, mechanical interactions, and single-cell expansion together shape self-organization during growth.
2512.01981
Dec 2025Soft Condensed Matter
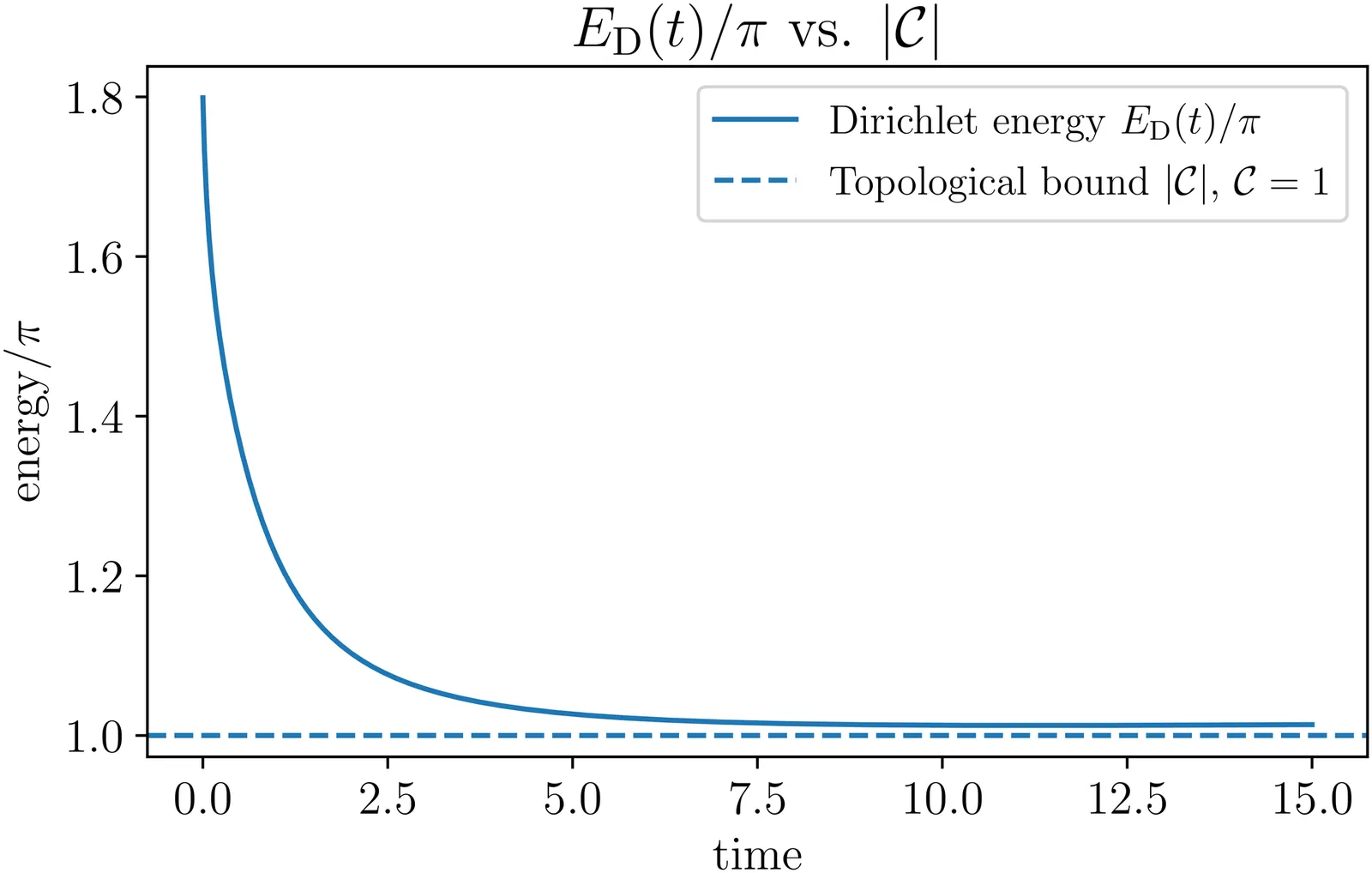
Relaxation to an Ideal Chern Band through Coupling to a Markovian Bath
We propose a microscopic, weak-coupling mechanism by which generic Chern bands relax toward ideal bands. We consider coupling interacting electrons to a Caldeira-Leggett like Ohmic bosonic bath. Using the Born-Markov approximation, Slater determinant states of a Chern band under Hartree-Fock approximation evolve toward Slater determinant states corresponding to an ideal Chern band. We validate our proposal by performing numerical simulation of a massive Dirac model, showing that the Berry curvature and quantum metric indeed co-evolve to saturate the trace condition. Our proposal provides a concrete dissipative route to realize ideal Chern bands, a fundamental building block for the stabilization of fractional Chern insulators.
2511.11394
Nov 2025Mesoscale and Nanoscale Physics
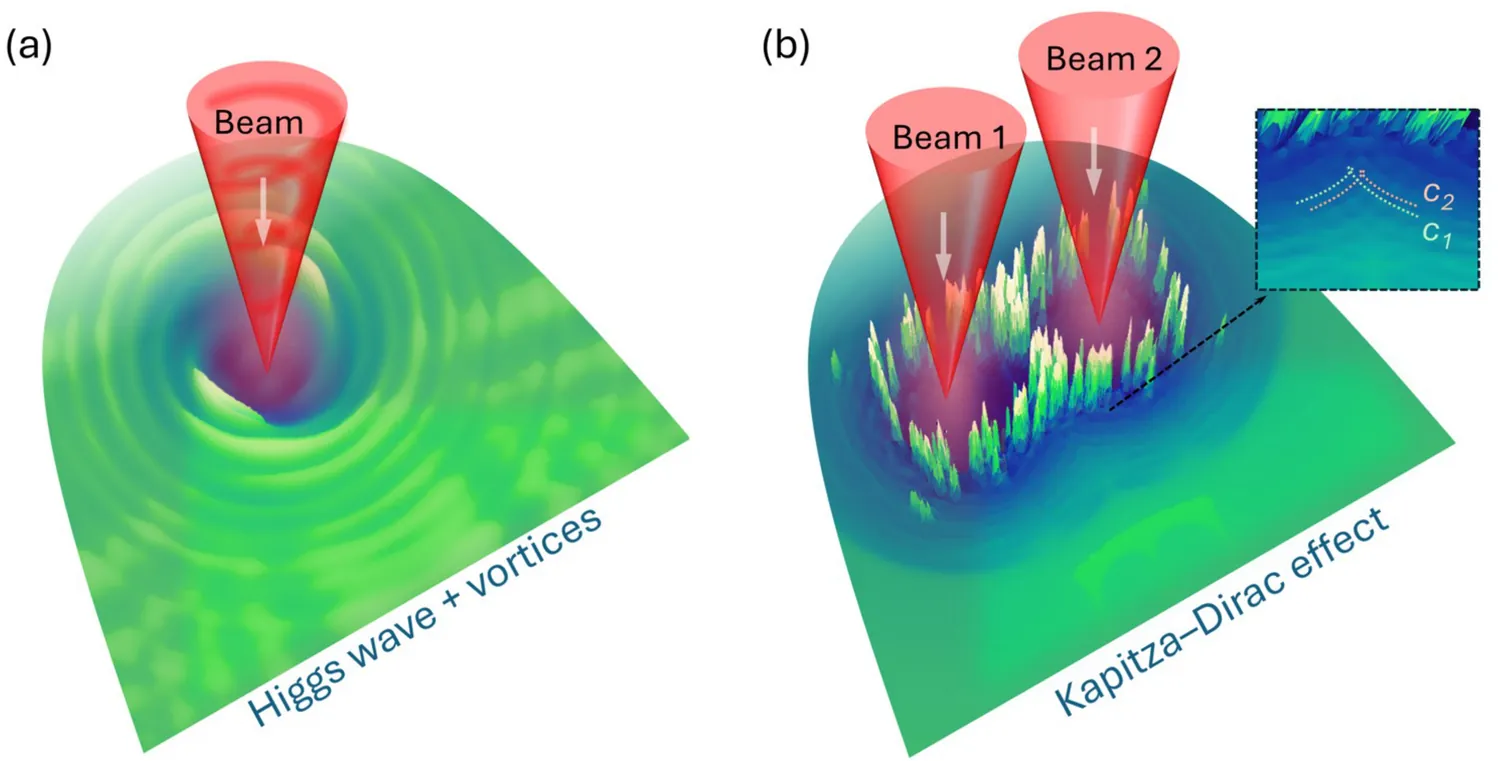
Kapitza-Dirac interference of Higgs waves in superconductors
We present a novel framework for controlling Higgs mode and vortex dynamics in superconductors using structured light. We propose a phenomenon analog of the Kapitza-Dirac effect in superconductors, where Higgs waves scatter off light-induced vortex lattices, generating interference patterns akin to matter wave diffraction. We also find that the vortices enable the linear coupling of Higgs mode to the electromagnetic field. This interplay between light-engineered Higgs excitations and emergent vortex textures opens a pathway to probe nonequilibrium superconductivity with unprecedented spatial and temporal resolution. Our results bridge quantum optics and condensed matter physics, offering new examples of quantum printing where one uses structured light to manipulate the collective modes in correlated quantum fluids.
2511.10954
Nov 2025Strongly Correlated Electrons
Nonequilibrium Thermodynamics of Associative Memory Continuous-Time Recurrent Neural Networks
Continuous-Time Recurrent Neural Networks (CTRNNs) have been widely used for their capacity to model complex temporal behaviour. However, their internal dynamics often remain difficult to interpret. In this paper, we propose a new class of CTRNNs based on Hopfield-like associative memories with asymmetric couplings. This model combines the expressive power of associative memories with a tractable mathematical formalism to characterize fluctuations in nonequilibrium dynamics. We show that this mathematical description allows us to directly compute the evolution of its macroscopic observables (the encoded features), as well as the instantaneous entropy and entropy dissipation of the system, thereby offering a bridge between dynamical systems descriptions of low-dimensional observables and the statistical mechanics of large nonequilibrium networks. Our results suggest that these nonequilibrium associative CTRNNs can serve as more interpretable models for complex sequence-encoding networks.
2511.11150
Nov 2025Disordered Systems and Neural Networks
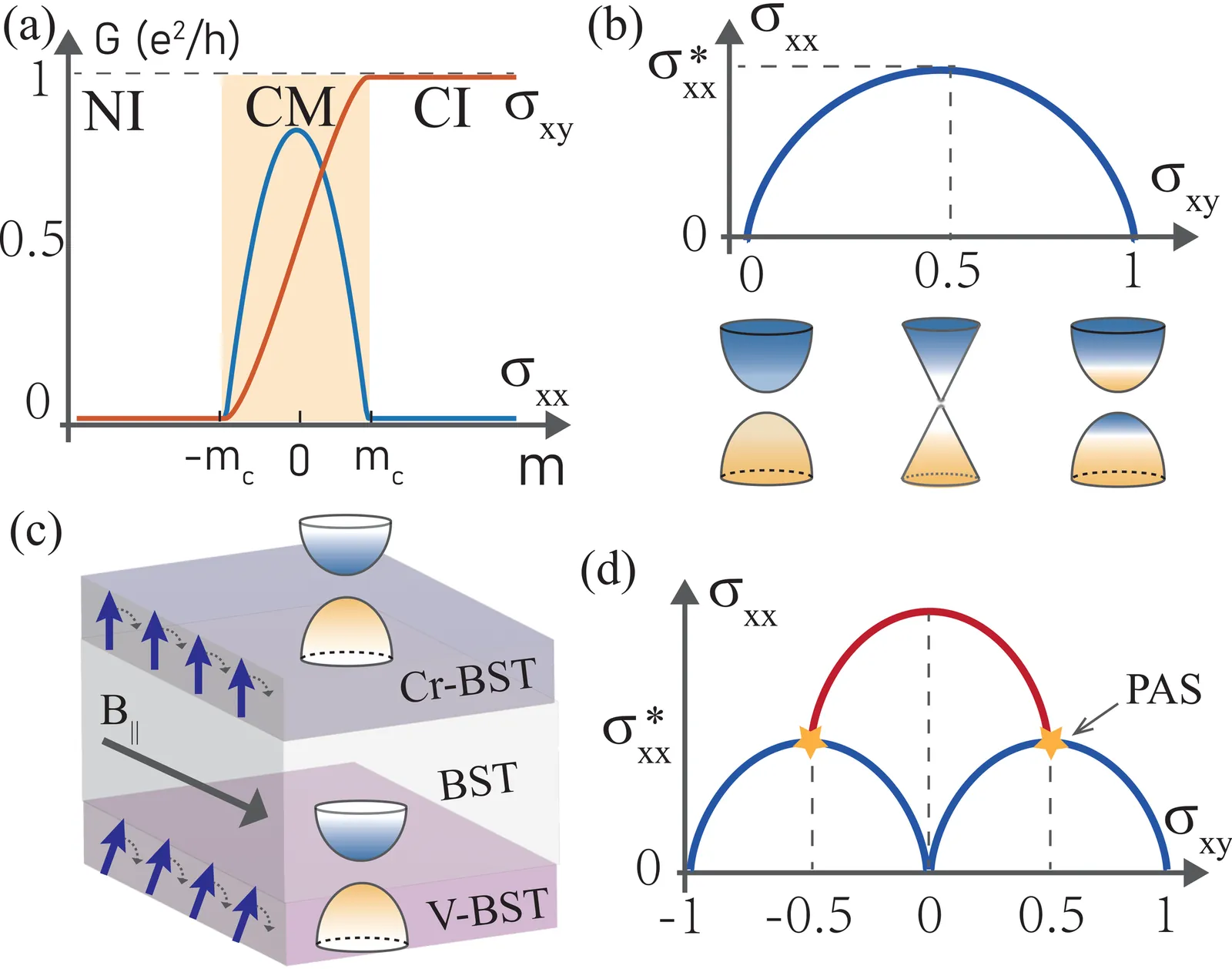
Nearly semi-elliptic relation between the minimal conductivity and Hall conductivity in unpaired Dirac fermions
Electric conductivities may reveal the topological and magnetic properties of band structures in solids, especially for two-dimensional unpaired Dirac fermions. In this work, we evaluate the longitudinal and Hall conductivity for unpaired Dirac fermions in the framework of the self-consistent Born approximation and find a nearly semi-elliptic relation between the minimal conductivity and Hall conductivities in the Dirac fermions. Near the charge neutrality point, disorder may drive a metal-insulator transition, and enhance the longitudinal conductivity. For the massless case, the minimal conductivity $σ_{xx}^*$ coexists with the half-quantized Hall conductivity $e^2/2h$, forming an indicator for the parity anomalous semimetal. The relation signals a disorder-induced metallic phase that bridges two topologically distinct insulating phases, and agrees with the recent experimental observation in magnetic topological insulators.
2511.10972
Nov 2025Mesoscale and Nanoscale Physics
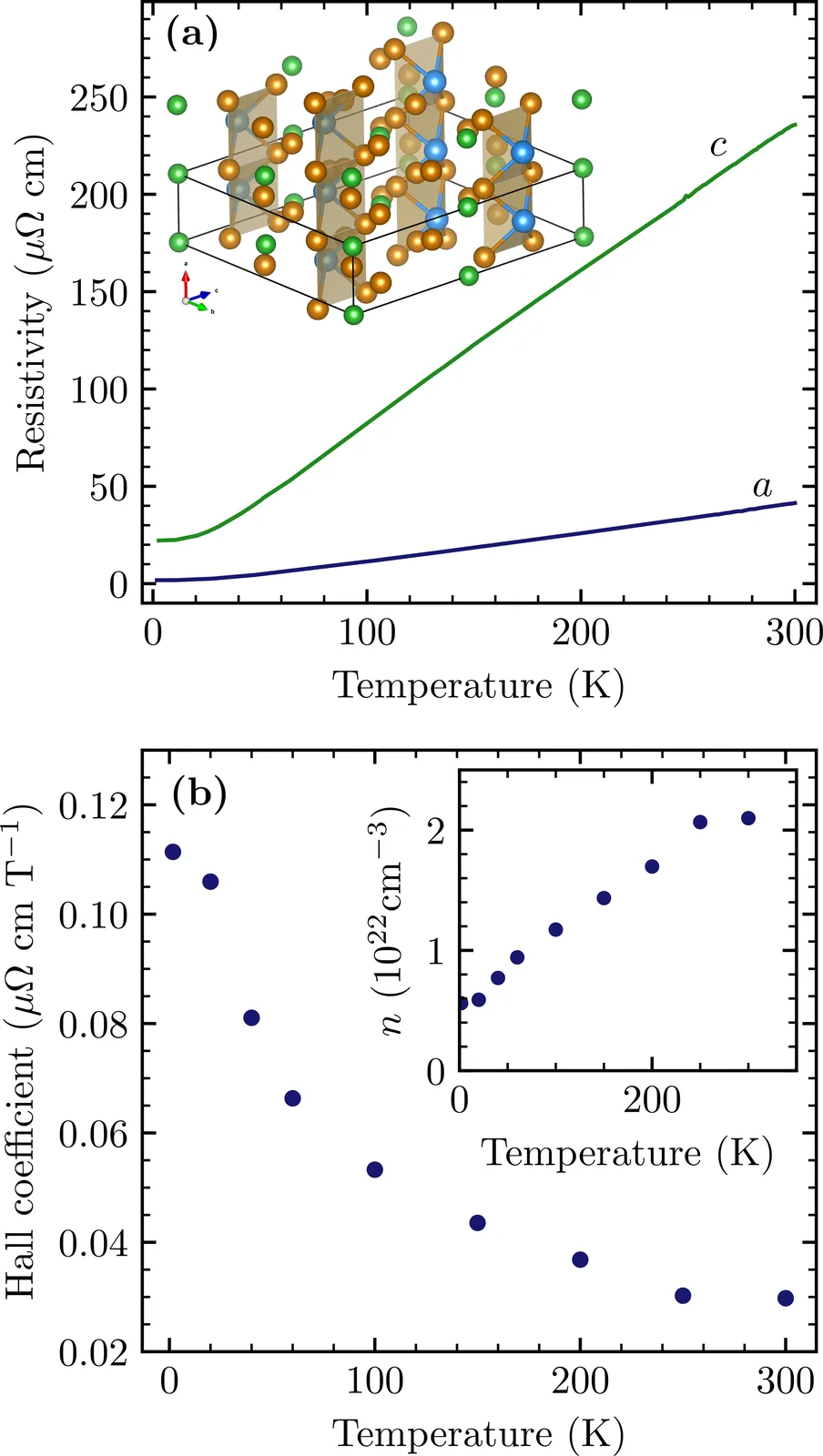
Optical conductivity of layered topological semimetal TaNiTe$_5$
We present an infrared spectroscopy study of the layered topological semimetal TaNiTe$_5$, a material with a quasi-one-dimensional structure and strong in-plane anisotropy. Despite its structural features, infrared reflectivity and electronic transport measurements along the $a$ and $c$ crystallographic axes show metallic behavior without evidence of reduced dimensionality. Optical conductivity reveals an anisotropic but conventional metallic response with low scattering rates and a single sharp infrared-active phonon mode at $396$ cm$^{-1}$ ($49$ meV). Ab initio calculations closely match the experimental optical data and confirm a three-dimensional electronic structure. Our results demonstrate that TaNiTe$_5$ behaves as a three-dimensional anisotropic semimetal in its electronic and optical properties.
2511.11105
Nov 2025Strongly Correlated Electrons