Strongly Correlated Electrons
Quantum magnetism, non-Fermi liquids, spin liquids, Mott insulators, heavy fermions.
Looking for a broader view? This category is part of:
Quantum magnetism, non-Fermi liquids, spin liquids, Mott insulators, heavy fermions.
Looking for a broader view? This category is part of:
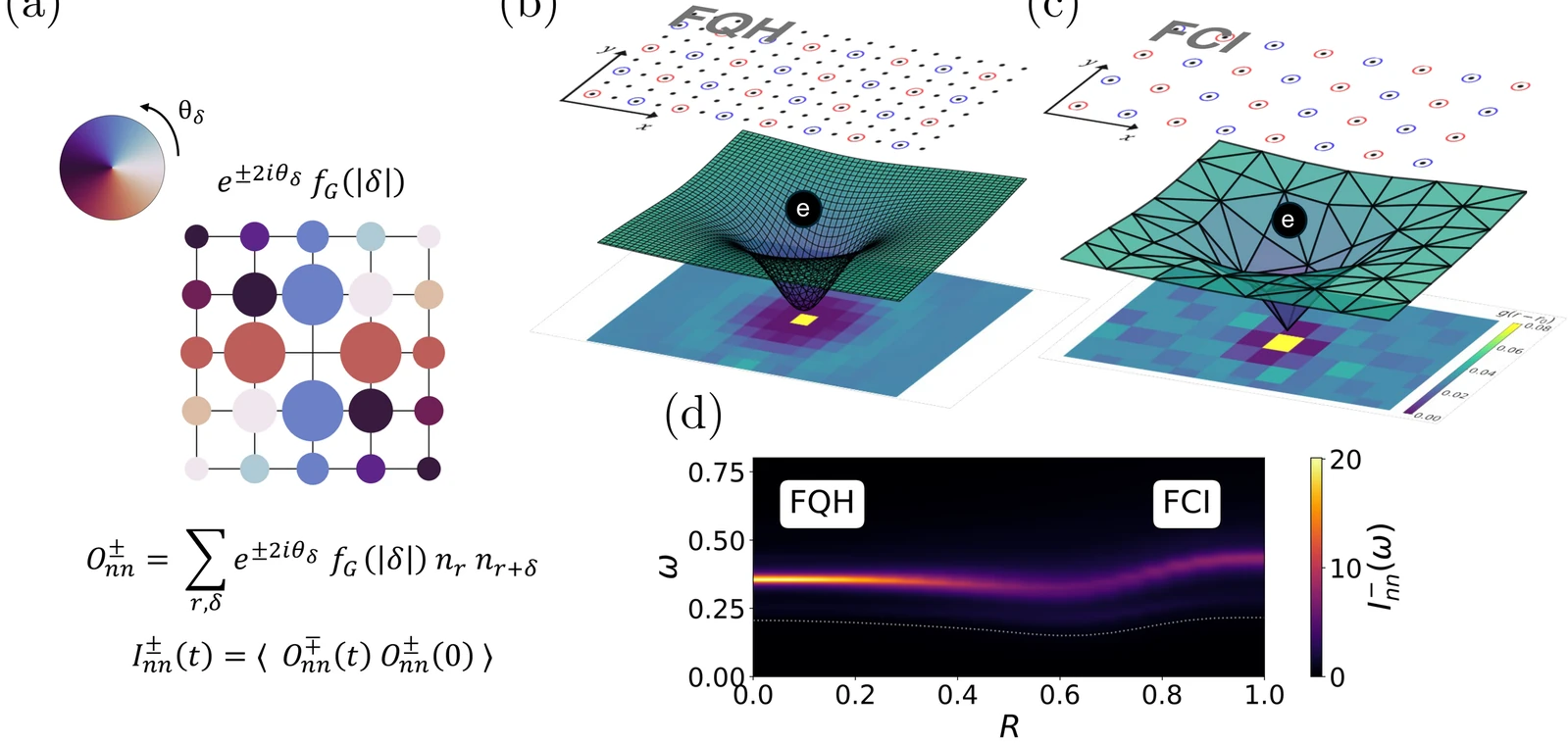
Chiral graviton modes are hallmark collective excitations of Fractional Quantum Hall (FQH) liquids. However, their existence on the lattice, where continuum symmetries that protect them from decay are lost, is still an open and urgent question, especially considering the recent advances in the realization of Fractional Chern Insulators (FCI) in transition metal dichalcogenides and rhombohedral pentalayer graphene. Here we present a comprehensive theoretical and numerical study of graviton-modes in fermionic FCI, and thoroughly demonstrate their existence. We first derive a lattice stress tensor operator in the context of the fermionic Harper-Hofstadter(HH) model which captures the graviton in the flat band limit. Importantly, we discover that such lattice stress-tensor operators are deeply connected to lattice quadrupolar density correlators, readily generalizable to generic Chern bands. We then explicitly show the adiabatic connection between FQH and FCI chiral graviton modes by interpolating from a low flux HH model to a Checkerboard lattice model that hosts a topological flat band. In particular, using state-of-the-art matrix product state and exact diagonalization simulations, we provide strong evidence that chiral graviton modes are long-lived excitations in FCIs despite the lack of continuous symmetries and the scattering with a two-magnetoroton continuum. By means of a careful finite-size analysis, we show that the lattice generates a finite but small intrinsic decay rate for the graviton mode. We discuss the relevance of our results for the exploration of graviton modes in FCI phases realized in solid state settings, as well as cold atom experiments.
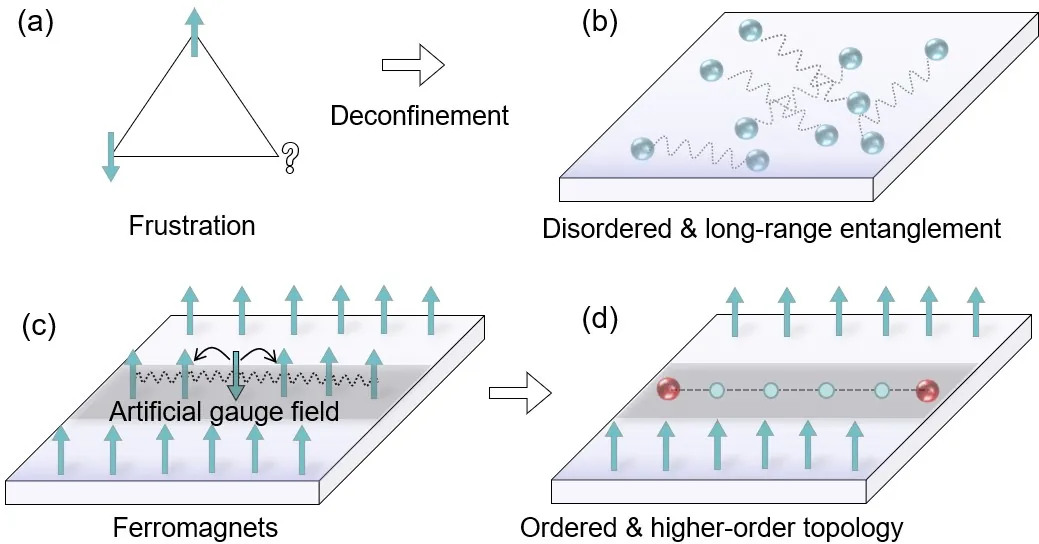
Spinons are elementary excitations at the core of frustrated quantum magnets. Although it is well-established that a pair of spinons can emerge from a magnon via deconfinement, controlled manipulation of individual spinons and direct observation of their deconfinement remain elusive. We propose an artificial gauge field scenario that enables the engineering of specific excited states in quantum spin models. This generates spatially localized individual spinons with high controllability. By applying time-dependent gauge fields, we realize adiabatic braiding of these spinons, as well as their dynamical evolution in a controllable manner. These results not only provide the first direct visualization of individual spinons localized in the bulk, but also point to new possibilities to simulate their confinement process. Finally, we demonstrate the feasibility of our scenario in Rydberg atoms, which suggests an experimentally viable direction--gauge field engineering of correlated phenomena in excited states.
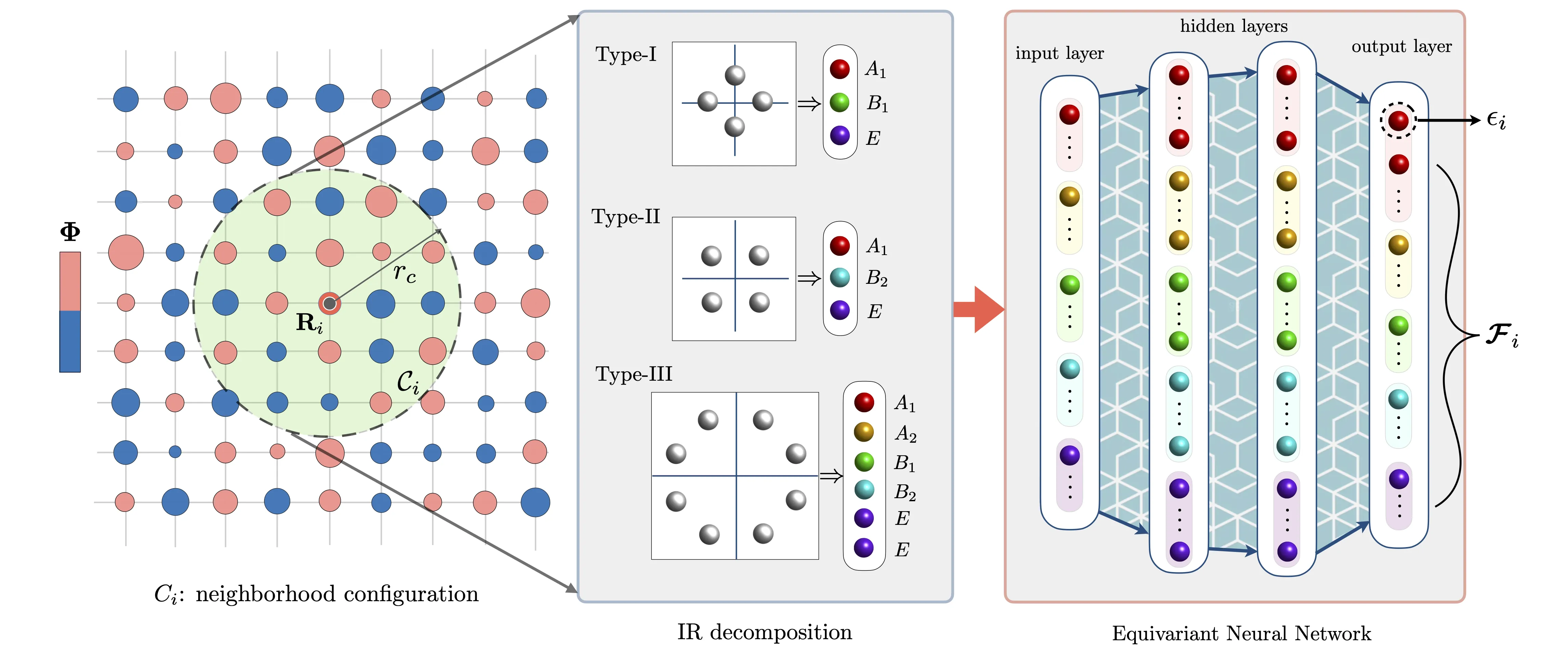
Machine-learning (ML) force fields enable large-scale simulations with near-first-principles accuracy at substantially reduced computational cost. Recent work has extended ML force-field approaches to adiabatic dynamical simulations of condensed-matter lattice models with coupled electronic and structural or magnetic degrees of freedom. However, most existing formulations rely on hand-crafted, symmetry-aware descriptors, whose construction is often system-specific and can hinder generality and transferability across different lattice Hamiltonians. Here we introduce a symmetry-preserving framework based on equivariant neural networks (ENNs) that provides a general, data-driven mapping from local configurations of dynamical variables to the associated on-site forces in a lattice Hamiltonian. In contrast to ENN architectures developed for molecular systems -- where continuous Euclidean symmetries dominate -- our approach aims to embed the discrete point-group and internal symmetries intrinsic to lattice models directly into the neural-network representation of the force field. As a proof of principle, we construct an ENN-based force-field model for the adiabatic dynamics of the Holstein Hamiltonian on a square lattice, a canonical system for electron-lattice physics. The resulting ML-enabled large-scale dynamical simulations faithfully capture mesoscale evolution of the symmetry-breaking phase, illustrating the utility of lattice-equivariant architectures for linking microscopic electronic processes to emergent dynamical behavior in condensed-matter lattice systems.
We highlight that integer Heisenberg groups at level 2 underlie topological quantum phenomena: their group algebras coincide with the algebras of quantum observables of abelian anyons in fractional quantum Hall (FQH) systems on closed surfaces. Decades ago, these groups were shown to arise as the fundamental groups of the space of maps from the surface to the 2-sphere -- which has recently been understood as reflecting an effective FQH flux quantization in 2-Cohomotopy. Here we streamline and generalize this theorem using the homotopy theory of H-groups, showing that for $k \in \{1,2,4\}$, the non-torsion part of $π_1 \mathrm{Map}\big({(S^{2k-1})^2, S^{2k}}\big)$ is an integer Heisenberg group of level 2, where we identify this level with 2 divided by the Hopf invariant of the generator of $π_{4k-1}(S^{2k})$. This result implies the existence of higher-dimensional analogs of FQH anyons in the cohomotopical completion of 11D supergravity ("Hypothesis H").
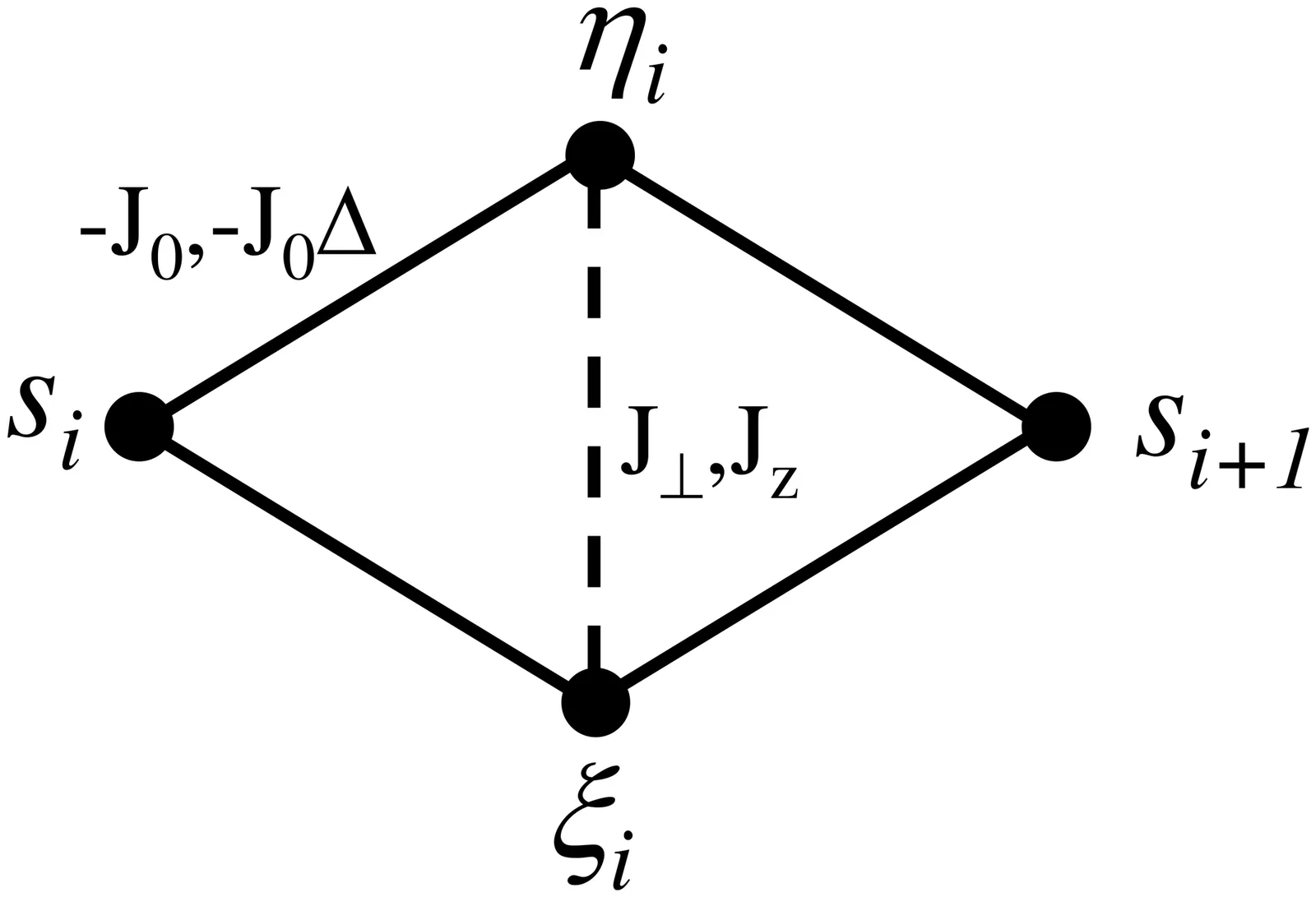
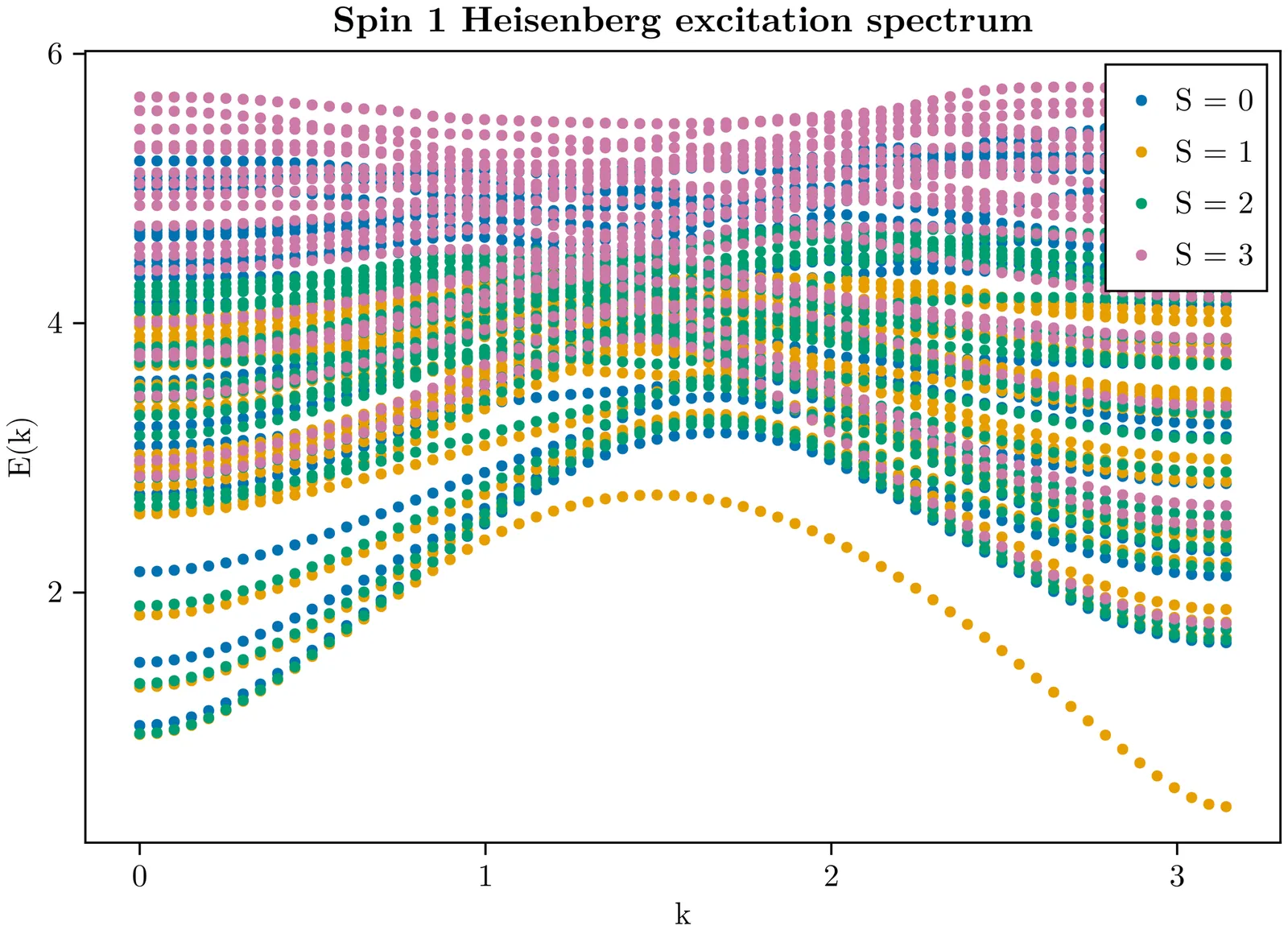
We study the ground state properties of the anisotropic spin-1/2 Heisenberg model on lattices built from ideal diamond units with competing ferro- and antiferromagnetic interactions. The study covers the one-dimensional diamond chain and its two- and three-dimensional generalizations. The ground-state phase diagram contains four distinct phases: ferromagnetic (F), critical (C), monomer-dimer (MD), and tetramer-dimer (TD), which converge at a quadruple point. We demonstrate the presence of macroscopic ground-state degeneracy and corresponding residual entropy, which is maximal at the quadruple point and also extends throughout the MD phase and its boundaries with TD and F phases. For the diamond chain, we derive exact degeneracies, while for higher-dimensional lattices, we map the problem onto a bond percolation model or used transfer-matrix approach, enabling the numerical computation of the ground state degeneracy.
 2601.01523
2601.01523..In this work, we investigate generalized symmetries, with particular emphasis on non-invertible ones, in three-dimensional non-Abelian topological orders hosting both particle- and loop-like excitations. We adopt a continuum topological field theory description, focusing on twisted $BF$ theories with gauge group $G=\prod_i \mathbb{Z}_{N_i}$ and an $a \wedge a \wedge b$ twisted term. This field theory supports Borromean-Rings braiding and realizes non-Abelian topological order, which for $G=(\mathbb{Z}_2)^3$ admits a microscopic realization via the $\mathbb{D}_4$ Kitaev quantum double lattice model. We systematically identify all generalized symmetry operators by extracting conserved currents from the equations of motion. Two distinct classes of currents emerge: type-I currents, which generate invertible higher-form symmetries, and type-II currents, which give rise to non-invertible higher-form symmetries. The non-invertibility originates from projectors accompanying the symmetry operators, which restrict admissible gauge-field configurations. We further analyze the fusion rules of these symmetries, showing that invertible symmetries admit inverses, while non-invertible symmetries fuse through multiple channels. Finally, we study mixed anomalies among these generalized symmetries by simultaneously coupling multiple currents to proper types of background gauge fields and examining their gaugeability. We identify two types of mixed anomalies: one cancellable by topological field theories in one higher dimension, and another representing an intrinsic gauging obstruction encoded in the $(3+1)$D continuum topological field theory...
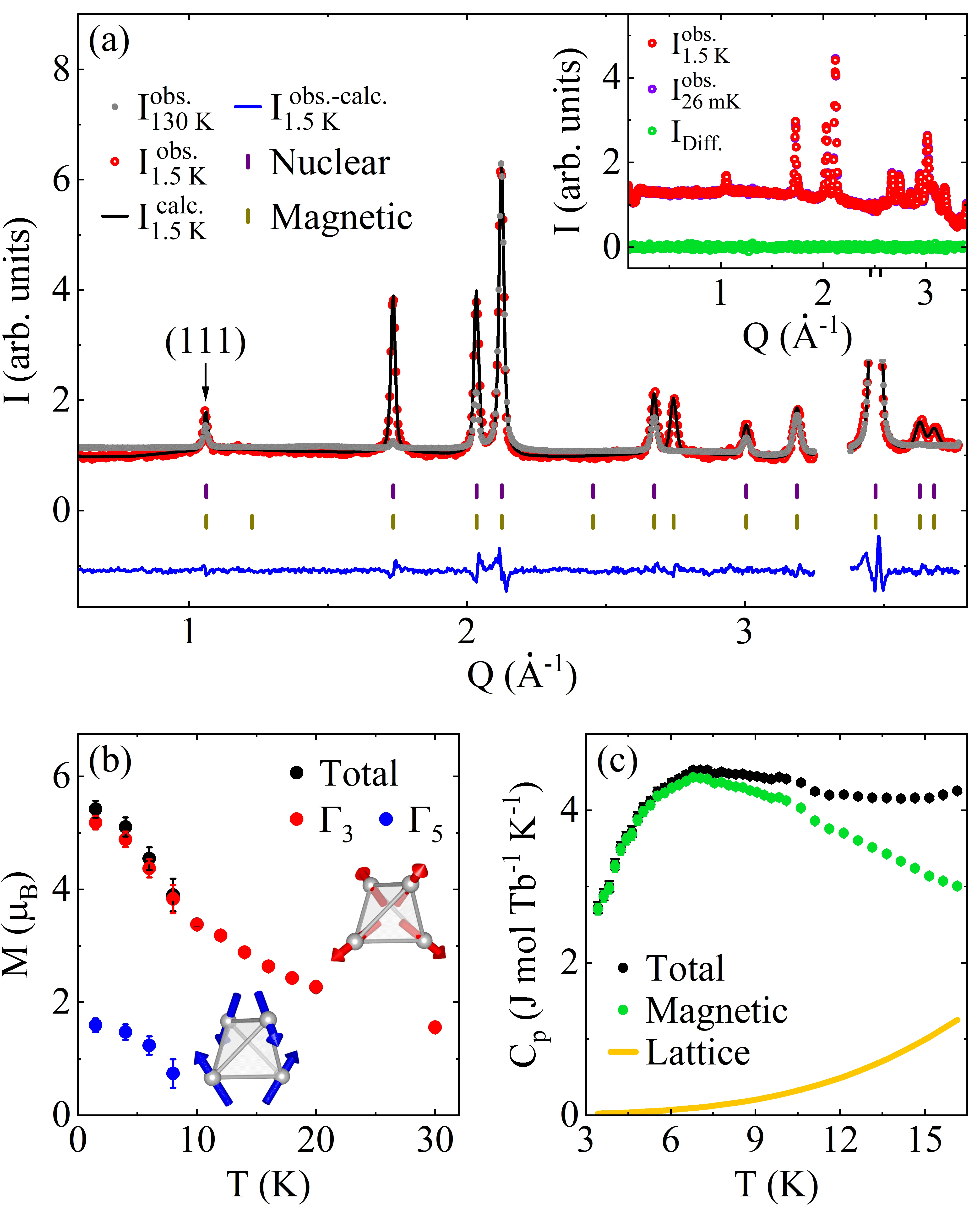
Magnetic-rare-earth pyrochlore iridates exhibit a rich variety of unconventional phases, driven by the complex interactions within and between the rare-earth and the iridium sublattices. In this study, we investigate the peculiar magnetic state of Tb$_{2}$Ir$_{2}$O$_{7}$, where a component of the Tb$^{3+}$ moment orders perpendicular to its local Ising anisotropy axis. By means of neutron diffraction and inelastic neutron scattering down to dilution temperatures, complemented by specific heat measurements, we show that this intriguing magnetic state is fully established at 1.5 K and we characterize its excitation spectrum across a broad range of energies. Our calculations reveal that bilinear interactions between Tb$^{3+}$ ions subjected to the Ir molecular field capture several key features of the experiments, but need to be supplemented to fully reproduce the observed behavior.
Supersymmetric conformal field theories (SCFTs) form a unique subset of quantum field theories which provide powerful insights into strongly coupled critical phenomena. Here, we present a microscopic and non-perturbative realization of the three-dimensional $\mathcal{N}=1$ superconformal Ising critical point, based on a Yukawa-type coupling between a 3D Ising CFT and a gauged Majorana fermion. Using the recently developed fuzzy sphere regularization, we directly extract the scaling dimensions of low-lying operators via the state-operator correspondence. At the critical point, we demonstrate conformal multiplet structure together with the hallmark of emergent spacetime supersymmetry through characteristic relations between fermionic and bosonic operators. Moreover, by tuning the Yukawa coupling, we explicitly track the evolution of operator spectra from the decoupled Ising-Majorana fixed point to the interacting superconformal fixed point, revealing renormalization-group flow at the operator level. Our results establish a controlled, non-perturbative microscopic route to 3D SCFTs.
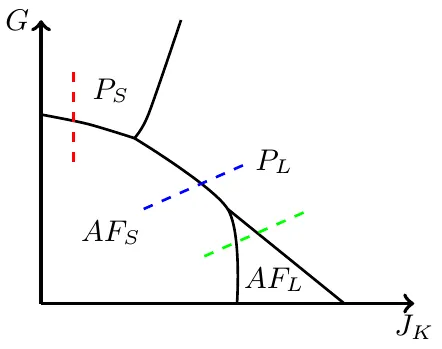
Strange metals represent a foundational problem in quantum condensed matter physics, and heavy fermion systems provide a canonical setting to advance a general understanding. The concept of a Kondo destruction quantum critical point is widely invoked to describe the competition of the Kondo effect and the local-moment magnetism. Here, we develop a unified field-theoretic approach, analyzing this competition from a rare approach that is anchored by the magnetically ordered side. Our analysis reveals, for the first time within a renormalization group framework, a quantum critical point across which the Kondo effect goes from being destroyed to dominating. Our findings elucidate not only the Kondo destruction quantum criticality but also an accompanying global phase diagram of heavy fermion metals.
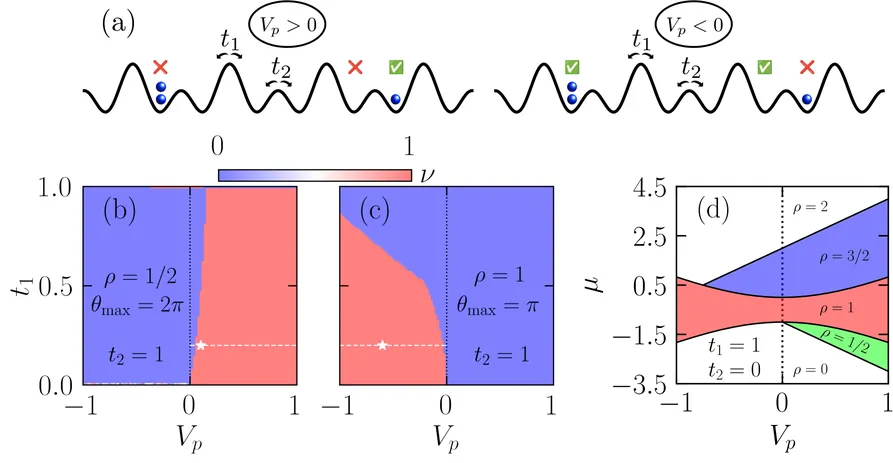
Symmetry-protected topological (SPT) phases in interacting bosonic systems have been extensively studied, yet most realizations rely on fine-tuned interactions or enlarged symmetries. Here we show that a qualitatively different mechanism--parity order coupled to bond dimerization--acts as a fundamental driver of bosonic topology. Using density matrix renormalization group simulations, we identify two distinct topological phases absent in the purely dimerized model: an SPT phase at half filling stabilized by positive parity coupling, and a topological phase at unit filling stabilized by negative coupling that can be adiabatically connected to a trivial phase without breaking any symmetry. Our results establish parity order as a new organizing principle for correlation-driven bosonic topology.
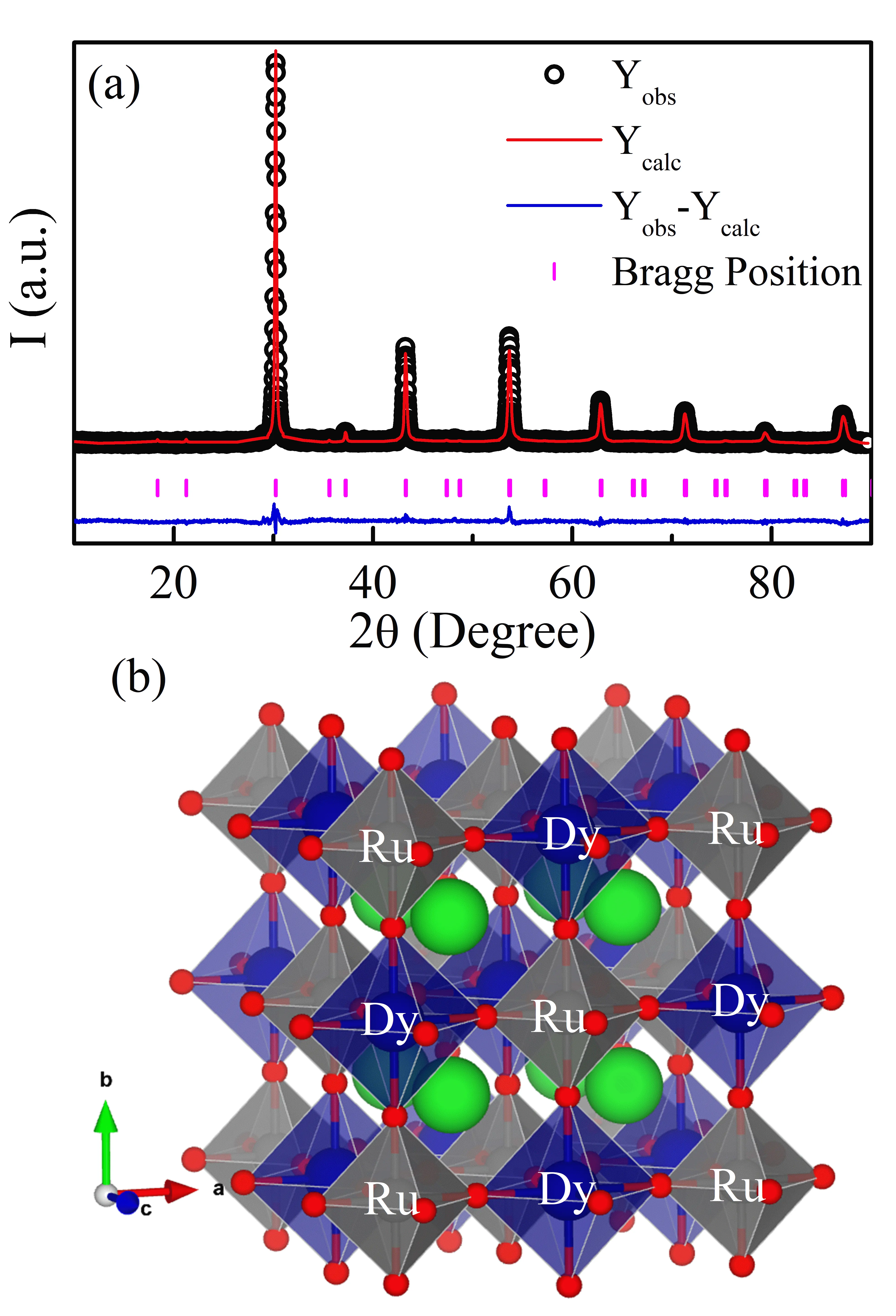
Double perovskites containing 4d--4f interactions provide a platform to study complex magnetic phenomena in correlated systems. Here, we investigate the magnetic ground state and quasiparticle excitations of the fascinating double perovskite system, Ba$_2$DyRuO$_6$, through Time of flight (TOF) neutron diffraction (TOF), inelastic neutron scattering (INS), and theoretical modelling. The compound Ba$_2$DyRuO$_6$ is reported to exhibit a single magnetic transition, in sharp contrast to most of the other rare-earth (R) members in this family, A$_2$RRuO$_6$ (A = Ca/Sr/Ba), which typically show magnetic ordering of the Ru ions, followed by R-ion ordering. Our neutron diffraction results confirm that long-range antiferromagnetic order emerges at $T_\mathrm{N} \approx 47$~K, primarily driven by 4d--4f Ru$^{5+}$--Dy$^{3+}$ exchange interactions, where both Dy and Ru moments start to order simultaneously. The ordered ground state is a collinear antiferromagnet with Ising character, carrying ordered moments of $μ_{\mathrm{Ru}} = 1.6(1)~μ_\mathrm{B}$ and $μ_{\mathrm{Dy}} = 5.1(1)~μ_\mathrm{B}$ at 1.5~K. Low-temperature INS reveals well-defined magnon excitations below 10~meV. SpinW modelling of the INS spectra evidences complex exchange interactions and the presence of magnetic anisotropy, which governs the Ising ground state and accounts for the observed magnon spectrum. Combined INS and Raman spectroscopy reveal crystal-electric-field (CEF) excitations of Dy$^{3+}$ at 46.5 and 71.8~meV in the paramagnetic region. The observed CEF levels are reproduced by point-charge calculations consistent with the $O_h$ symmetry of Dy$^{3+}$. A complementary machine-learning approach is used to analyse the phonon spectrum and compare with INS data. Together, these results clarify the origin of phonon and magnon excitations and their role in the ground-state magnetism of Ba$_2$DyRuO$_6$.
We apply methods of equivariant homotopy theory, which may not previously have found due attention in condensed matter physics, to classify first the fragile/unstable topological phases of 2D crystalline Chern insulator materials, and second the possible topological order of their fractional cousins. We highlight that the phases are given by the equivariant 2-Cohomotopy of the Brillouin torus of crystal momenta (with respect to wallpaper point group actions) -- which, despite the attention devoted to crystalline Chern insulators, seems not to have been considered before. Arguing then that any topological order must be reflected in the adiabatic monodromy of gapped quantum ground states over the covariantized space of these band topologies, we compute the latter in examples where this group is non-abelian, showing that any potential FQAH anyons must be localized in momentum space. We close with an outlook on the relevance for the search for topological quantum computing hardware. Mathematical details are spelled out in a supplement.
Tensor networks provide a powerful new framework for classifying and simulating correlated and topological phases of quantum matter. Their central premise is that strongly correlated matter can only be understood by studying the underlying entanglement structure and its associated (generalised) symmetries. In essence, tensor networks provide a compressed, holographic description of the complicated vacuum fluctuations in strongly correlated systems, and as such they break down the infamous many-body exponential wall. These lecture notes provide a concise overview of the most important conceptual, computational and mathematical aspects of this theory.
Two of the iconic phases of the hole-doped cuprate materials are the intermediate temperature pseudogap metal and the lower temperature $d$-wave superconductor. Following the prescient suggestion of P.W. Anderson, there were numerous early theories of these phases as doped quantum spin liquids. However, these theories have had difficulties with two prominent observations: (i) angle-dependent magnetoresistance measurements (ADMR), including observation of the Yamaji effect, present convincing evidence of small hole pockets which can tunnel coherently between square lattice layers, and (ii) the velocities of the nodal Bogoliubov quasiparticles in the $d$-wave superconductor are highly anisotropic, with $v_F \gg v_Δ$. These lecture notes review how the fractionalized Fermi Liquid (FL*) state, which dopes quantum spin liquids with gauge-neutral electron-like quasiparticles, resolves both difficulties. Theories of insulating quantum spin liquids employing fractionalization of the electron spin into bosonic or fermionic partons are discussed. Doping the bosonic parton theory leads to a holon metal theory: while not appropriate for the cuprate pseudogap, this theory is argued to apply to the Lieb lattice. Doping the fermionic parton theory leads to a $d$-wave superconductor with nearly isotropic quasiparticle velocities. The construction of the FL* state is described using a quantum dimer model, followed by a more realistic description using the Ancilla Layer Model (ALM), which is then used to obtain the theory of the pseudogap and the $d$-wave superconductor.
 2512.23706
2512.23706Gapless quantum phases can become distinct when internal symmetries are enforced, in analogy with gapped symmetry-protected topological (SPT) phases. However, this distinction does not always lead to protected edge modes, raising the question of how the bulk-boundary correspondence is generalized to gapless cases. We propose that the spatial interface between gapless phases -- rather than their boundaries -- provides a more robust fingerprint. We show that whenever two 1+1d conformal field theories (CFTs) differ in symmetry charge assignments of local operators or twisted sectors, any symmetry-preserving spatial interface between the theories must flow to a non-invertible defect. We illustrate this general result for different versions of the Ising CFT with $\mathbb{Z}_2 \times \mathbb{Z}_2^T$ symmetry, obtaining a complete classification of allowed conformal interfaces. When the Ising CFTs differ by nonlocal operator charges, the interface hosts 0+1d symmetry-breaking phases with finite-size splittings scaling as $1/L^3$, as well as continuous phase transitions between them. For general gapless phases differing by an SPT entangler, the interfaces between them can be mapped to conformal defects with a certain defect 't Hooft anomaly. This classification also gives implications for higher-dimensional examples, including symmetry-enriched variants of the 2+1d Ising CFT. Our results establish a physical indicator for symmetry-enriched criticality through symmetry-protected interfaces, giving a new handle on the interplay between topology and gapless phases.
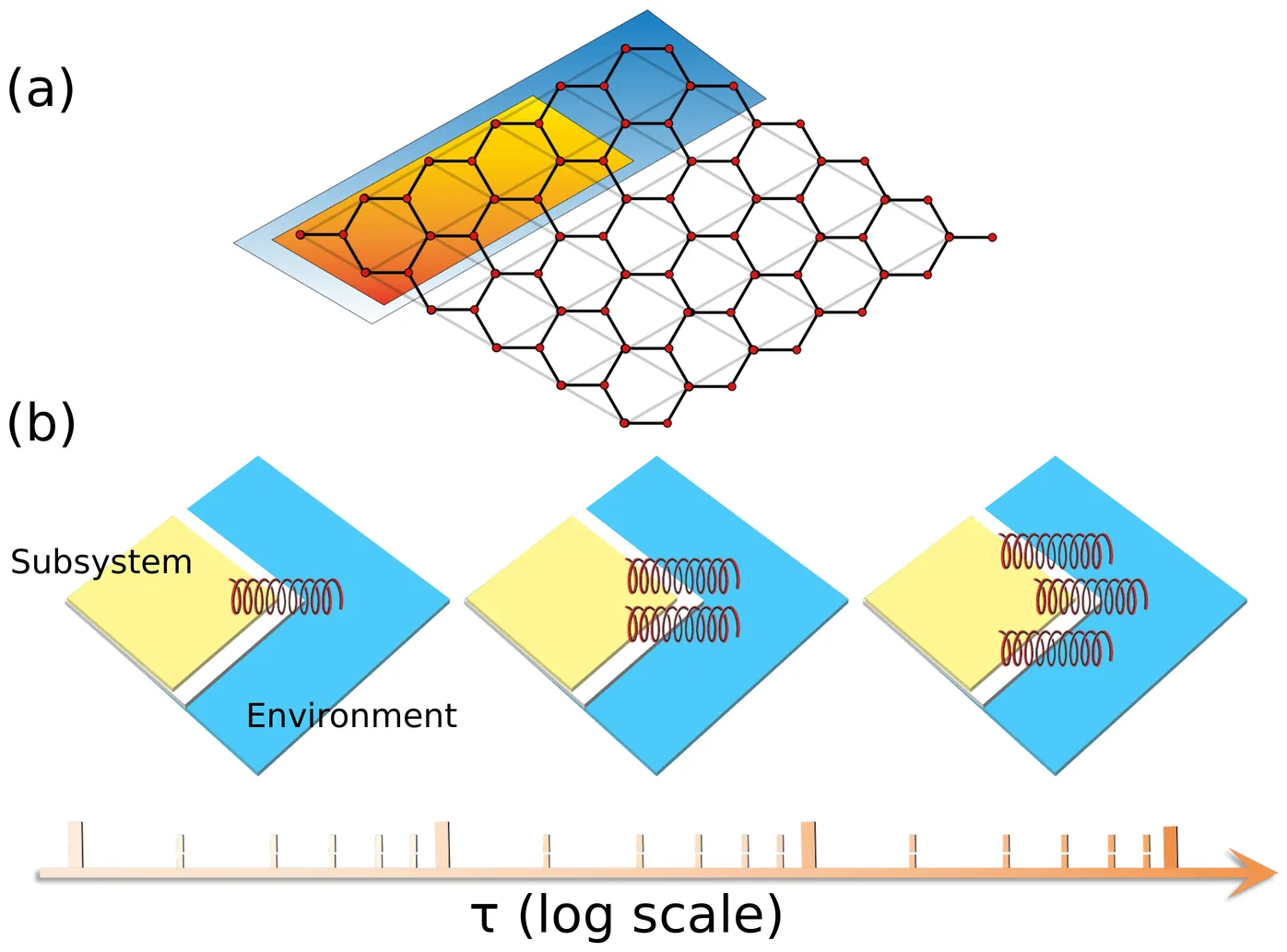
Characterizing universal entanglement features in higher-dimensional quantum matter is a central goal of quantum information science and condensed matter physics. While the subleading corner terms in two-dimensional quantum systems encapsulate essential universal information of the underlying conformal field theory, our understanding of these features remains remarkably limited compared to their one-dimensional counterparts. We address this challenge by investigating the entanglement dynamics of fermionic systems along the imaginary-time evolution. We uncover a pioneering non-equilibrium scaling law where the corner entanglement entropy grows linearly with the logarithm of imaginary time, dictated solely by the universality class of the quantum critical point. Through unbiased Quantum Monte Carlo simulations, we verify this scaling in the interacting Gross-Neveu-Yukawa model, demonstrating that universal data can be accurately recovered from the early stages of relaxation. Our findings significantly circumvent the computational bottlenecks inherent in reaching full equilibrium convergence. This work establishes a direct link between the fundamental theory of non-equilibrium critical phenomena and the high-precision determination of universal entanglement properties on both classical and quantum platforms, paving the way for probing the rich entanglement structure of quantum critical systems.
Charge-$4e$ superconductors are phases where quartets of electrons condense in the absence of Cooper pairing condensation. They exhibit distinctive signatures including fractional flux quantization and anomalous Josephson effects, and are actively being explored in strongly correlated systems, such as moiré materials. In this work we develop a general framework for \emph{topological} charge-$2ne$ superconductors based on both wavefunction and field theory approaches. In particular, we generate topological charge-$2ne$ superconductors from charge-$2e$ ingredients, and by breaking the charge $U(1)$ symmetry in certain classes of quantum Hall states. Via bulk-edge correspondence, we further construct the corresponding edge conformal field theory and bulk topological quantum field theory for topological charge-$2ne$ superconductors that suggests fermionic nonabelian topological orders. Our results provide a unified low energy description of the topological charge-$2ne$ superconductivity, offer a concrete platform for studying symmetry breaking and enrichment in interacting topological phases of matter, and have direct implications for experimental probes such as quasiparticle interferometry.
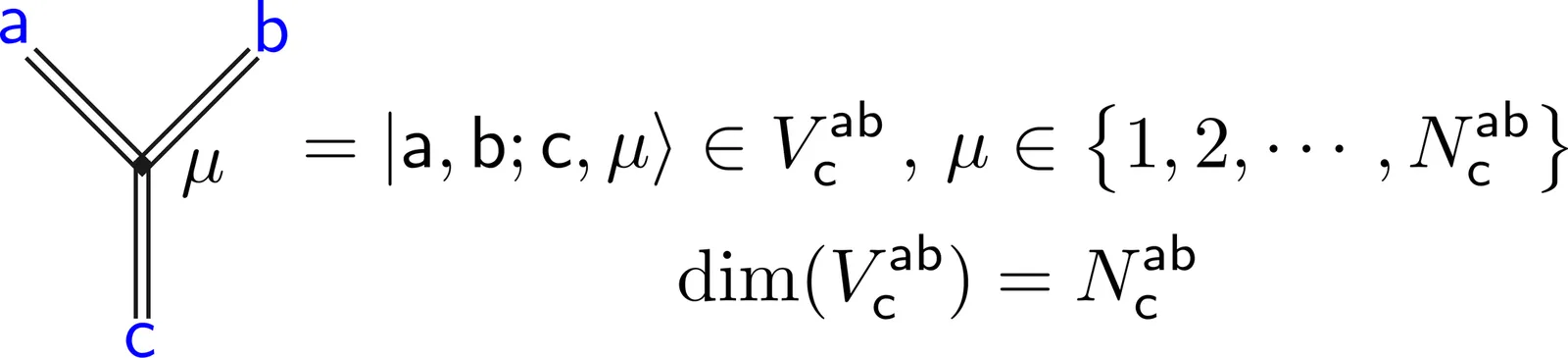
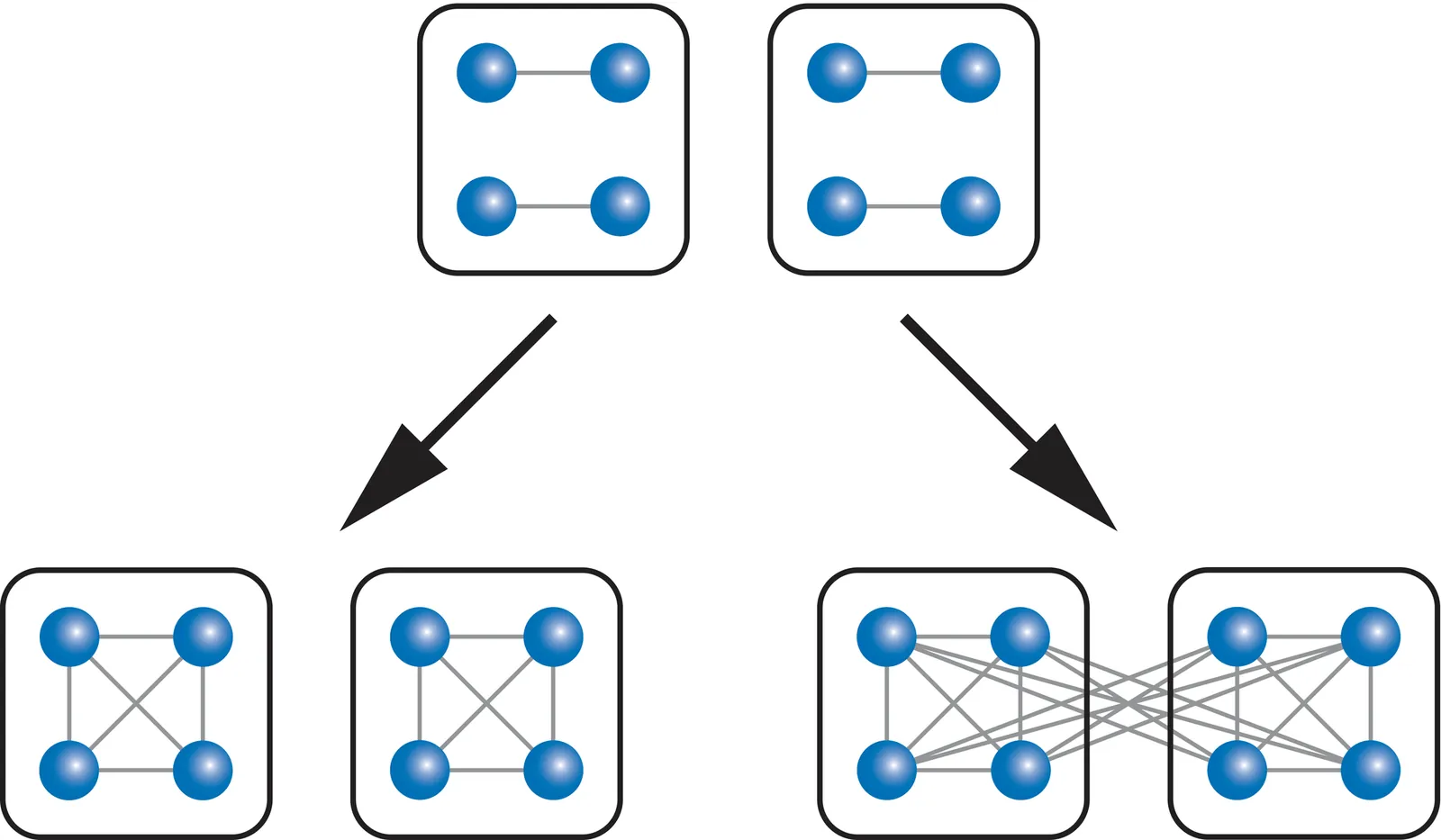
Here we provide a microscopic lattice construction of excitations, fusion, and shrinking in a non-Abelian topological order by studying the three-dimensional quantum double model. We explicitly construct lattice operators that create, fuse, and shrink particle and loop excitations, systematically derive their fusion and shrinking rules, and demonstrate that non-Abelian shrinking channels can be controllably selected through internal degrees of freedom of loop operators. Most importantly, we show that the lattice shrinking rules obey the fusion--shrinking consistency relations predicted by twisted $BF$ field theory, providing solid evidence for the validity of field-theoretical principles developed over the past years. In particular, we compute the full set of excitations, fusion, and shrinking data at the microscopic lattice level and verify exact agreement between the microscopic $\mathbb{D}_4$ quantum double lattice model and the continuum $BF$ field theory with an $AAB$ twist and $(\mathbb{Z}_2)^3$ gauge group, thereby placing the latter field theory, originally discovered in 2018 in connection with Borromean-ring braiding, on a solid microscopic footing. Our results bridge continuum topological field theory and exactly solvable lattice models, elevate fusion--shrinking consistency from a continuum field-theoretical principle to a genuine topological phenomenon defined at the microscopic lattice scale, and provide a concrete microscopic foundation for experimentally engineering higher-dimensional non-Abelian topological orders in controllable quantum simulators, such as trapped-ion systems.
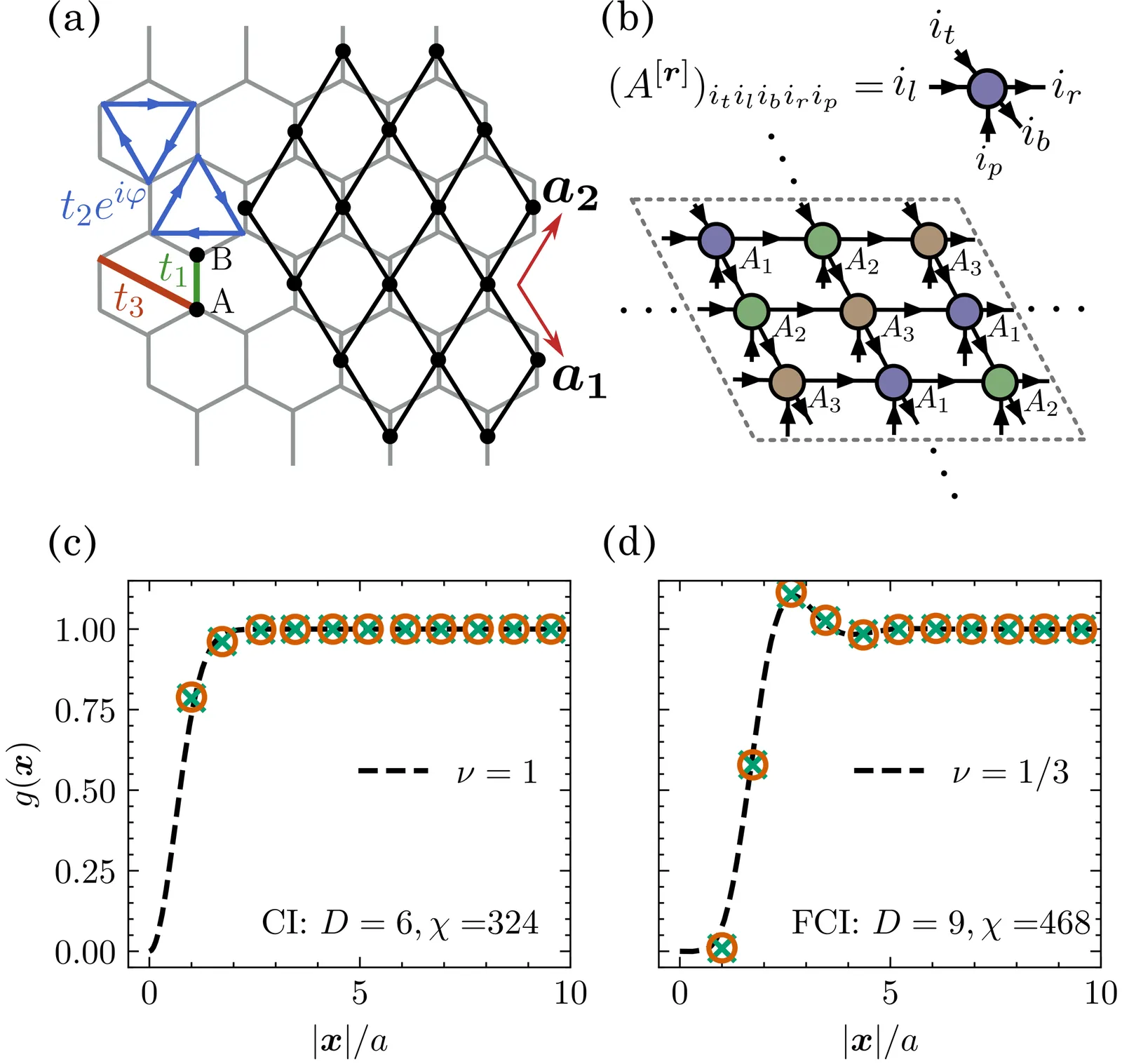
Infinite projected entangled-pair states (iPEPS) provide a powerful variational framework for two-dimensional quantum matter and have been widely used to capture bosonic topological order, including chiral spin liquids. Here we extend this approach to \emph{fermionic} topological order by variationally optimizing $U(1)$-symmetric fermionic iPEPS for a fractional Chern insulator (FCI), with bond dimensions up to $D=9$. We find evidence for a critical bond dimension, above which the ansatz faithfully represents the FCI phase. The FCI state is characterized using bulk observables, including the equal-time single-particle Green's function and the pair-correlation function, as well as the momentum-resolved edge entanglement spectrum. To enable entanglement-spectrum calculations for large iPEPS unit cells, we introduce a compression scheme and show that the low-lying part of the spectrum is already well converged at relatively small cutoff dimensions.
 2512.20608
2512.20608We propose a ground state entanglement probe for gapped, two-dimensional quantum many-body systems that involves taking powers of reduced density matrices in a particular geometric configuration. This quantity, which we denote by $ω_{α,β}$, is parameterized by two positive real numbers $α, β$, and can be seen as a ``Rényi-like" generalization of the modular commutator -- another entanglement probe proposed as a way to compute the chiral central charge from a bulk wave function. We obtain analytic expressions for $ω_{α,β}$ for gapped ground states of non-interacting fermion Hamiltonians as well as ground states of string-net models. In both cases, we find that $ω_{α,β}$ takes a universal value related to the chiral central charge. For integer values of $α$ and $β$, our quantity $ω_{α,β}$ can be expressed as an expectation value of permutation operators acting on an appropriate replica system, providing a natural route to measuring $ω_{α,β}$ in numerical simulations and potentially, experiments.