Condensed Matter

Materials science, superconductivity, mesoscale physics, and quantum materials

Includes:Mesoscale and Nanoscale Physics(cond-mat.mes-hall)Materials Science(cond-mat.mtrl-sci)Strongly Correlated Electrons(cond-mat.str-el)Superconductivity(cond-mat.supr-con)Statistical Mechanics(cond-mat.stat-mech)

Trending in Condensed Matter

Large language models and the entropy of English

We use large language models (LLMs) to uncover long-ranged structure in English texts from a variety of sources. The conditional entropy or code length in many cases continues to decrease with context length at least to $N\sim 10^4$ characters, implying that there are direct dependencies or interactions across these distances. A corollary is that there are small but significant correlations between characters at these separations, as we show from the data independent of models. The distribution of code lengths reveals an emergent certainty about an increasing fraction of characters at large $N$. Over the course of model training, we observe different dynamics at long and short context lengths, suggesting that long-ranged structure is learned only gradually. Our results constrain efforts to build statistical physics models of LLMs or language itself.

2512.24969

Dec 2025Statistical Mechanics

About the origin of the magnetic ground state of Tb$_{2}$Ir$_{2}$O$_{7}$

Magnetic-rare-earth pyrochlore iridates exhibit a rich variety of unconventional phases, driven by the complex interactions within and between the rare-earth and the iridium sublattices. In this study, we investigate the peculiar magnetic state of Tb$_{2}$Ir$_{2}$O$_{7}$, where a component of the Tb$^{3+}$ moment orders perpendicular to its local Ising anisotropy axis. By means of neutron diffraction and inelastic neutron scattering down to dilution temperatures, complemented by specific heat measurements, we show that this intriguing magnetic state is fully established at 1.5 K and we characterize its excitation spectrum across a broad range of energies. Our calculations reveal that bilinear interactions between Tb$^{3+}$ ions subjected to the Ir molecular field capture several key features of the experiments, but need to be supplemented to fully reproduce the observed behavior.

2601.00749

Jan 2026Strongly Correlated Electrons

Symmetric approximant formalism for statistical topological matter

The standard approach to characterizing topological matter, computing topological invariants, fails when the symmetry protecting the topological phase is preserved only on average in a disordered system. Because topological invariants rely on enforcing the symmetry exactly, they can overcount phases by incorrectly identifying certain non-robust features as robust. Moreover, in intrinsic statistical topological insulators, enforcing the symmetry exactly is guaranteed to destroy the topological phase. We define a mapping that addresses both issues and provides a unified framework for describing disordered topological matter.

2601.00784

Jan 2026Mesoscale and Nanoscale Physics

2601.00294

Bridging Commutant and Polynomial Methods for Hilbert Space Fragmentation

A quantum model exhibits Hilbert space fragmentation (HSF) if its Hilbert space decomposes into exponentially many dynamically disconnected subspaces, known as Krylov subspaces. A model may however have different HSFs depending on the method for identifying them. Here we establish a connection between two vastly distinct methods recently proposed for identifying HSF: the commutant algebra (CA) method and integer characteristic polynomial factorization (ICPF) method. For a Hamiltonian consisting of operators admitting rational number matrix representations, we prove a theorem that, if its center of commutant algebra have all eigenvalues being rational, the HSF from the ICPF method must be equal to or finer than that from the CA method. We show that this condition is satisfied by most known models exhibiting HSF, for which we demonstrate the validity of our theorem. We further discuss representative models for which ICPF and CA methods yield different HSFs. Our results may facilitate the exploration of a unified definition of HSF.

2601.00294

Jan 2026Statistical Mechanics

Pseudo-Hermitian Magnon Dynamics

A defining quantity of a physical system is its energy which is represented by the Hamiltonian. In closed quantum mechanical or/and coherent wave-based systems the Hamiltonian is introduced as a Hermitian operator which ensures real energy spectrum and secures the decomposition of any state over a complete basis set spanning the space where the states live. Pseudo-Hermitian, or PT symmetric, systems are a special class of non-Hermitian ones. They describe open systems but may still have real energy spectrum. The eigenmodes are however not orthogonal in general. This qualitative difference to Hermitian physics has a range of consequences for the physical behaviour of the system in the steady state or when it is subjected to external perturbations. This overview reviews the recent progress in the field of pseudo-Hermitian physics as it unfolds when applied to low-energy excitations of magnetically ordered materials. The focus is mainly on long wave length spin excitations (spin waves) with magnons being the energy quanta of these excitations. Various setups including ferromagnetic, antiferromagnetic, magnonic crystals, and hybride structures with different types of coupling to the environments as well as spatio-temporally engineered systems will be discussed with a focus on the particular aspects that are brought about by the pseudo-Hermiticity such as mode amplifications, non-reciprocal propagation, magnon cloaking, non-Hermitian skin effect, PT-symmetric assisted Floquet engineering, topological energy transfer, and field-induced enhanced sensitivity.

2601.00701

Jan 2026Mesoscale and Nanoscale Physics

Les Houches Lectures Notes on Tensor Networks

Tensor networks provide a powerful new framework for classifying and simulating correlated and topological phases of quantum matter. Their central premise is that strongly correlated matter can only be understood by studying the underlying entanglement structure and its associated (generalised) symmetries. In essence, tensor networks provide a compressed, holographic description of the complicated vacuum fluctuations in strongly correlated systems, and as such they break down the infamous many-body exponential wall. These lecture notes provide a concise overview of the most important conceptual, computational and mathematical aspects of this theory.

2512.24390

Dec 2025Strongly Correlated Electrons

Lectures on insulating and conducting quantum spin liquids

Two of the iconic phases of the hole-doped cuprate materials are the intermediate temperature pseudogap metal and the lower temperature $d$-wave superconductor. Following the prescient suggestion of P.W. Anderson, there were numerous early theories of these phases as doped quantum spin liquids. However, these theories have had difficulties with two prominent observations: (i) angle-dependent magnetoresistance measurements (ADMR), including observation of the Yamaji effect, present convincing evidence of small hole pockets which can tunnel coherently between square lattice layers, and (ii) the velocities of the nodal Bogoliubov quasiparticles in the $d$-wave superconductor are highly anisotropic, with $v_F \gg v_Δ$. These lecture notes review how the fractionalized Fermi Liquid (FL*) state, which dopes quantum spin liquids with gauge-neutral electron-like quasiparticles, resolves both difficulties. Theories of insulating quantum spin liquids employing fractionalization of the electron spin into bosonic or fermionic partons are discussed. Doping the bosonic parton theory leads to a holon metal theory: while not appropriate for the cuprate pseudogap, this theory is argued to apply to the Lieb lattice. Doping the fermionic parton theory leads to a $d$-wave superconductor with nearly isotropic quasiparticle velocities. The construction of the FL* state is described using a quantum dimer model, followed by a more realistic description using the Ancilla Layer Model (ALM), which is then used to obtain the theory of the pseudogap and the $d$-wave superconductor.

2512.23962

Dec 2025Strongly Correlated Electrons

Emergence of 3D Superconformal Ising Criticality on the Fuzzy Sphere

Supersymmetric conformal field theories (SCFTs) form a unique subset of quantum field theories which provide powerful insights into strongly coupled critical phenomena. Here, we present a microscopic and non-perturbative realization of the three-dimensional $\mathcal{N}=1$ superconformal Ising critical point, based on a Yukawa-type coupling between a 3D Ising CFT and a gauged Majorana fermion. Using the recently developed fuzzy sphere regularization, we directly extract the scaling dimensions of low-lying operators via the state-operator correspondence. At the critical point, we demonstrate conformal multiplet structure together with the hallmark of emergent spacetime supersymmetry through characteristic relations between fermionic and bosonic operators. Moreover, by tuning the Yukawa coupling, we explicitly track the evolution of operator spectra from the decoupled Ising-Majorana fixed point to the interacting superconformal fixed point, revealing renormalization-group flow at the operator level. Our results establish a controlled, non-perturbative microscopic route to 3D SCFTs.

2512.25054

Dec 2025Strongly Correlated Electrons

An introduction to monitored quantum systems and quantum trajectories: spectrum, typicality, and phases

Thanks to recent experimental advances in simulating and detecting quantum dynamics with high precision and controllability, our understanding of the physics of monitored quantum systems has considerably deepened over the past decades. In this article, we provide an introductory theoretical review on the basic formalisms governing open quantum dynamics under measurement, along with recent developments in their spectral and typical aspects. After reviewing quantum measurement theory, we introduce the concept of quantum trajectories, which are the conditional dynamics of monitored states shaped by a set of measurement outcomes. We then discuss the spectral properties of the dynamical map describing the evolution averaged over measurement outcomes. As has recently been recognized, these spectral features are intimately connected to whether quantum trajectories exhibit typical behaviors, such as the ergodicity and purification. Moreover, we introduce Lyapunov exponents of typical quantum trajectories and discuss how these quantities serve as indicators of measurement-induced phase transitions in monitored quantum many-body systems.

2512.19922

Dec 2025Statistical Mechanics

X-ray magnetic circular dichroism of altermagnet $α$-Fe$_2$O$_3$ based on multiplet ligand-field theory using Wannier orbitals

Hematite $α$-Fe$_2$O$_3$ is a $g$-wave altermagnetic material, which has an easy-axis phase and easy-plane weak ferromagnetic phase below and above Morin transition temperature, respectively. The presence of these phases renders it a good candidate to study the characteristic spin splitting in altermagnets under the impacts of relativistic effect and finite temperature. In this regard, we have calculated the band structure of $α$-Fe$_2$O$_3$ based on density functional theory (DFT) which also considers the Hubbard-U correction and spin-orbit coupling (SOC) effects. Additionally, the charge self-consistent DFT + dynamical mean-field theory (DMFT) calculations have been performed at finite temperatures. It is found that the altermagnetic spin splitting in $α$-Fe$_2$O$_3$ preserves with either SOC or temperature effect taken into account. Furthermore, we present a numerical simulation of the x-ray magnetic circular dichroism (XMCD) of the L$_{2,3}$ edge of Fe using a combination of DFT with multiplet ligand-field theory (MLFT). In terms of the different Néel vectors present in $α$-Fe$_2$O$_3$, we calculate the x-ray absorption spectroscopy (XAS) of the L$_{2,3}$ edge of Fe in the form of conductivity tensor and analyze the XMCD response from a perspective of symmetry. A characteristic XMCD line shape is expected when the Néel vector is along [010] direction (magnetic point group $2^\prime/m^\prime$) and the light propagation vector is perpendicular to the Néel vector, which can be further distinguished from the XMCD response originated from weak ferromagnetism with the light propagation vector parallel to the Néel vector.

2512.11664

Dec 2025Materials Science

Electric and spin-valley currents induced by structured light in 2D Dirac materials

Structured optical fields can be used for the injection and control of charge and spin-valley currents. Here, we present a systematical study of these phenomena for interband absorption of structured light in 2D Dirac materials. We derive general expressions for the current density and the quasi-classical generation rate of photoelectrons in the momentum, coordinate, and spin-valley spaces. We reveal mechanisms of the current formation determined by the local and non-local contributions to the optical generation, including the mechanisms related to optical alignment of electron momenta by linearly polarized light, optical orientation by circularly polarized light, and the class of charge and spin-valley photon drags sensitive to the phase and polarization profiles of the optical field. We develop a kinetic theory of electric and spin-valley currents driven by the optical field with spatially inhomogeneous intensity, polarization, and phase and obtain analytical expressions for the current contributions. The theory is applied to analyze the photocurrents emerging in TMDC layers and graphene excited by polarization gratings.

2512.11677

Dec 2025Mesoscale and Nanoscale Physics

Curvilinear magnonic crystal based on 3D hierarchical nanotemplates

Curvilinear magnetic nanostructures enable control of magnetization dynamics through geometry-induced anisotropy and chiral interactions as well as magnetic field modulation. In this work, we report a curvilinear magnonic crystal based on large-area square arrays of truncated nanospikes fabricated by conformal coating of 3D hierarchical templates with permalloy thin films. Brillouin light scattering spectroscopy reveals anisotropic band structure with multiple dispersive and folded Bloch-type dispersive spin-wave modes as well as non-dispersive modes exhibiting direction-dependent frequency shifts and intensity asymmetries along lattice principal axes. Finite element micromagnetic simulations indicate that curvature-induced variations of the demagnetizing field govern the magnonic response, enabling the identification of modes propagating in nanochannels and other localized on nanospike apexes or along the ridges connecting adjacent nanospikes. The combination of geometric curvature and optical probing asymmetry produces directional dependence of magnonic bands, establishing 3D hierarchical templates as a versatile platform for curvature-engineered magnonics.

2512.11663

Dec 2025Strongly Correlated Electrons

Influence of Exchange-Correlation Functionals and Neural Network Architectures on Li$^+$-Ion Conductivity in Solid-State Electrolyte from Molecular Dynamics Simulations with Machine-Learning Force Fields

With the rapid advancement of machine learning techniques for materials simulations, machine-learned force fields (MLFFs) have become a powerful tool that complements first-principles calculations by enabling high-accuracy molecular dynamics simulations over extended timescales. Typically, MLFFs are trained on data generated from density functional theory (DFT) using a specific exchange-correlation (XC) functional, with the goal of reproducing DFT-level properties. However, the uncertainties in MLFF-based simulations--arising from variations in both MLFF model architectures and the choice of XC functionals--remain insufficiently understood. In this work, we construct MLFF models of different architectures trained on DFT data from both semilocal and hybrid functionals to describe Li$^+$ diffusion in the solid-state electrolyte Li$_6$PS$_5$Cl. We systematically investigate how different XC functionals influence the Li$^+$ diffusion coefficient. To reduce statistical uncertainty, the mean squared displacements are averaged over 300 independent molecular dynamics (MD) trajectories of 70 ps each, yielding statistical variations below $1\%$. This enables a clear assessment of the respective influences of the functional and the MLFF model. Due to its tendency to underestimate band gaps and migration barriers, the semilocal functional predicts consistently higher Li$^+$ diffusion coefficients, compared to the hybrid functional. Furthermore, comparisons among various neural network methods reveal that the differences in predicted diffusion coefficients arising from different network architectures are of the same order of magnitude as those caused by different functionals, indicating that the choice of the network model itself substantially influences the MLFF predictions. This observation calls from an urgent need for standardized protocols to minimize model-dependent biases in MLFF-based MD.

2512.11650

Dec 2025Materials Science

2512.03148

Proof that Momentum Mixing Hatsugai Kohmoto equals the Twisted Hubbard Model

We prove formally that the momentum-mixing Hatsugai-Kohmoto model (MMHK) is the Hubbard model with a twist. With this result in tow, we rely on the proof of Watanabe's that two models which differ by a twist must have the same bulk physics. Consequently, we have proven that MMHK=Hubbard in the charge sector.

2512.03148

Dec 2025Strongly Correlated Electrons

Relaxation to an Ideal Chern Band through Coupling to a Markovian Bath

We propose a microscopic, weak-coupling mechanism by which generic Chern bands relax toward ideal bands. We consider coupling interacting electrons to a Caldeira-Leggett like Ohmic bosonic bath. Using the Born-Markov approximation, Slater determinant states of a Chern band under Hartree-Fock approximation evolve toward Slater determinant states corresponding to an ideal Chern band. We validate our proposal by performing numerical simulation of a massive Dirac model, showing that the Berry curvature and quantum metric indeed co-evolve to saturate the trace condition. Our proposal provides a concrete dissipative route to realize ideal Chern bands, a fundamental building block for the stabilization of fractional Chern insulators.

2511.11394

Nov 2025Mesoscale and Nanoscale Physics

Kapitza-Dirac interference of Higgs waves in superconductors

We present a novel framework for controlling Higgs mode and vortex dynamics in superconductors using structured light. We propose a phenomenon analog of the Kapitza-Dirac effect in superconductors, where Higgs waves scatter off light-induced vortex lattices, generating interference patterns akin to matter wave diffraction. We also find that the vortices enable the linear coupling of Higgs mode to the electromagnetic field. This interplay between light-engineered Higgs excitations and emergent vortex textures opens a pathway to probe nonequilibrium superconductivity with unprecedented spatial and temporal resolution. Our results bridge quantum optics and condensed matter physics, offering new examples of quantum printing where one uses structured light to manipulate the collective modes in correlated quantum fluids.

2511.10954

Nov 2025Strongly Correlated Electrons

Nearly semi-elliptic relation between the minimal conductivity and Hall conductivity in unpaired Dirac fermions

Electric conductivities may reveal the topological and magnetic properties of band structures in solids, especially for two-dimensional unpaired Dirac fermions. In this work, we evaluate the longitudinal and Hall conductivity for unpaired Dirac fermions in the framework of the self-consistent Born approximation and find a nearly semi-elliptic relation between the minimal conductivity and Hall conductivities in the Dirac fermions. Near the charge neutrality point, disorder may drive a metal-insulator transition, and enhance the longitudinal conductivity. For the massless case, the minimal conductivity $σ_{xx}^*$ coexists with the half-quantized Hall conductivity $e^2/2h$, forming an indicator for the parity anomalous semimetal. The relation signals a disorder-induced metallic phase that bridges two topologically distinct insulating phases, and agrees with the recent experimental observation in magnetic topological insulators.

2511.10972

Nov 2025Mesoscale and Nanoscale Physics

Optical conductivity of layered topological semimetal TaNiTe$_5$

We present an infrared spectroscopy study of the layered topological semimetal TaNiTe$_5$, a material with a quasi-one-dimensional structure and strong in-plane anisotropy. Despite its structural features, infrared reflectivity and electronic transport measurements along the $a$ and $c$ crystallographic axes show metallic behavior without evidence of reduced dimensionality. Optical conductivity reveals an anisotropic but conventional metallic response with low scattering rates and a single sharp infrared-active phonon mode at $396$ cm$^{-1}$ ($49$ meV). Ab initio calculations closely match the experimental optical data and confirm a three-dimensional electronic structure. Our results demonstrate that TaNiTe$_5$ behaves as a three-dimensional anisotropic semimetal in its electronic and optical properties.

2511.11105

Nov 2025Strongly Correlated Electrons

Impact of spin-orbit coupling and Zeeman interaction on the subharmonic gap structure due to multiple Andreev reflections in nanoscopic Josephson junctions

Multiple Andreev reflections in voltage-biased Josephson junctions give rise to the subharmonic gap structure in the conductance, which is widely used to characterize transport properties and estimate the induced gap in the junctions. Here we theoretically investigate the evolution of the subharmonic gap structure in spinful Josephson junctions. Spin mixing introduced by the spin-orbit coupling opens avoided crossings in the dispersion relation of the leads, which, as we demonstrate, subsequently results in pronounced multiple Andreev reflection features in the conductance traces. We analyze how these features evolve under an external magnetic field and explain that their visibility in conductance is governed by the spin polarization of the bands.

2511.11277

Nov 2025Mesoscale and Nanoscale Physics

Interpretable descriptors enable prediction of hydrogen-based superconductors at moderate pressures

Room temperature superconductivity remains elusive, and hydrogen-base compounds despite remarkable transition temperatures(Tc) typically require extreme pressures that hinder application. To accelerate discovery under moderate pressures, an interpretable framework based on symbolic regression is developed to predict Tc in hydrogen-based superconductors. A key descriptor is an integrated density of states (IDOS) within 1 eV of the Fermi level (EF), which exhibits greater robustness than conventional single-point DOS features. The resulting analytic model links electronic-structure characteristics to superconducting performance, achieves high accuracy (RMSEtrain = 20.15 K), and generalizes well to external datasets. By relying solely on electronic structure calculations, the approach greatly accelerates materials screening. Guided by this model, four hydrogen-based candidates are identified and validated via calculation: Na2GaCuH6 with Tc =42.04 K at ambient pressure (exceeding MgB2), and NaCaH12, NaSrH12, and KSrH12 with Tc up to 162.35 K, 86.32 K, and 55.13 K at 100 GPa, 25 GPa, and 25 GPa, respectively. Beyond rapid screening, the interpretable form clarifies how hydrogen-projected electronic weight near EF and related features govern Tc in hydrides, offering a mechanism-aware route to stabilize high-Tc phases at reduced pressures.

2511.11284

Nov 2025Superconductivity

3,580 papers

Stochastic Path Compression for Spectral Tensor Networks on Cyclic Graphs

We develop a new approach to compress cyclic tensor networks called stochastic path compression (SPC) that uses an iterative importance sampling procedure to target edges with large bond-dimensions. Closed random walks in SPC form compression pathways that spatially localize large bond-dimensions in the tensor network. Analogous to the phase separation of two immiscible liquids, SPC separates the graph of bond-dimensions into spatially distinct high and low density regions. When combined with our integral decimation algorithm, SPC facilitates the accurate compression of cyclic tensor networks with continuous degrees of freedom. To benchmark and illustrate the methods, we compute the absolute thermodynamics of $q$-state clock models on two-dimensional square lattices and an XY model on a Watts-Strogatz graph, which is a small-world network with random connectivity between spins.

2601.04172Jan 2026

View

Universality in driven systems with a multiply-degenerate umbilic point

We investigate a driven particle system, a multilane asymmetric exclusion process, where the particle number in every lane is conserved, and stationary state is fully uncorrelated. The phase space has, starting from three lanes and more, an umbilic manifold where characteristic velocities of all the modes but one coincide, thus allowing us to study a weakly hyperbolic system with arbitrarily large degeneracy. We then study space-time fluctuations in the steady state, at the umbilic manifold, which are expected to exhibit universal scaling features. We formulate an effective mode-coupling theory (MCT) for the multilane model within the umbilic subspace and test its predictions. Unlike in the bidirectional two-lane model with an umbilic point studied earlier, here we find a robust $z=3/2$ dynamical exponent for the umbilic mode. The umbilic scaling function, obtained from Monte-Carlo simulations, for the simplest 3-lane scenario, appears to have an universal shape for a range of interaction parameters. Remarkably, the shape and dynamic exponent of the non-degenerate mode can be analytically predicted on the base of effective MCT, up to non-universal scaling factor. Our findings suggest the existence of novel universality classes with dynamical exponent $3/2$, appearing in long-lived hydrodynamic modes with equal characteristic velocities.

2601.04116Jan 2026

View

Equivariant Neural Networks for Force-Field Models of Lattice Systems

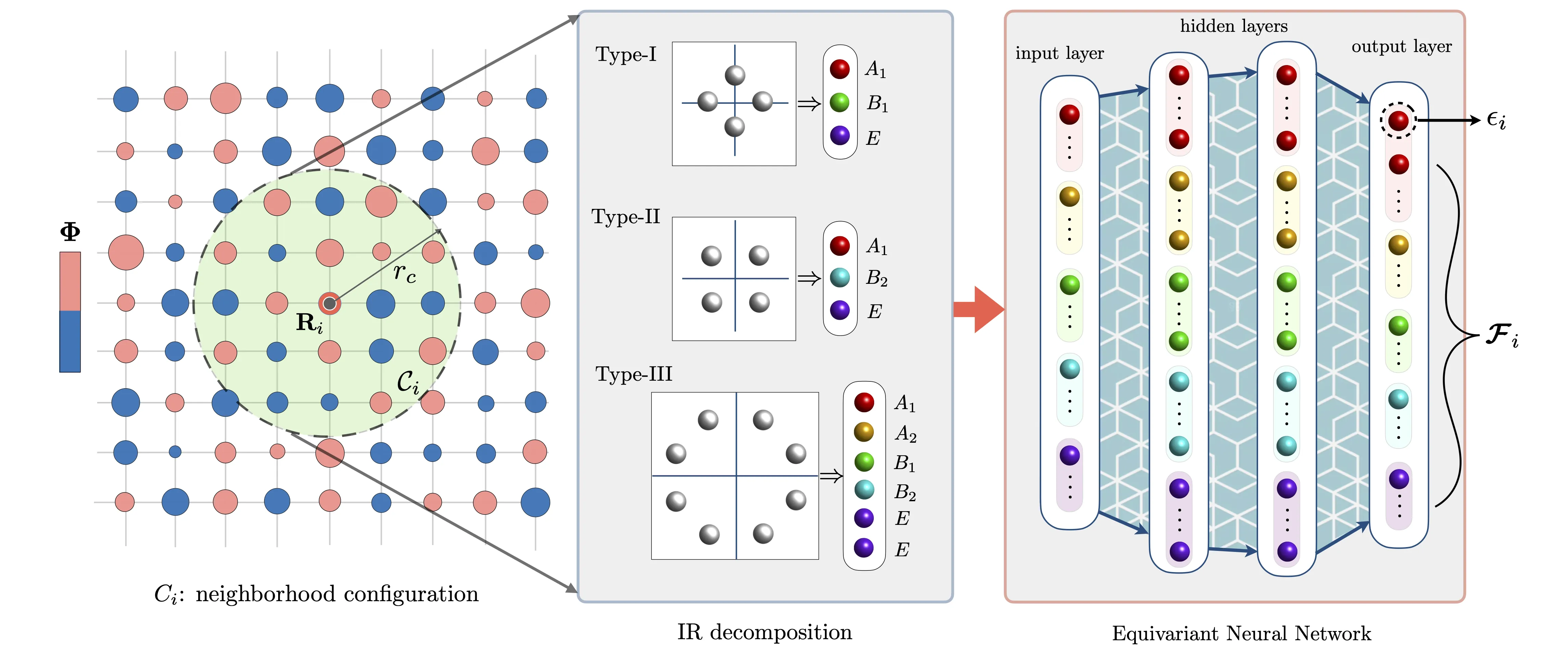
Machine-learning (ML) force fields enable large-scale simulations with near-first-principles accuracy at substantially reduced computational cost. Recent work has extended ML force-field approaches to adiabatic dynamical simulations of condensed-matter lattice models with coupled electronic and structural or magnetic degrees of freedom. However, most existing formulations rely on hand-crafted, symmetry-aware descriptors, whose construction is often system-specific and can hinder generality and transferability across different lattice Hamiltonians. Here we introduce a symmetry-preserving framework based on equivariant neural networks (ENNs) that provides a general, data-driven mapping from local configurations of dynamical variables to the associated on-site forces in a lattice Hamiltonian. In contrast to ENN architectures developed for molecular systems -- where continuous Euclidean symmetries dominate -- our approach aims to embed the discrete point-group and internal symmetries intrinsic to lattice models directly into the neural-network representation of the force field. As a proof of principle, we construct an ENN-based force-field model for the adiabatic dynamics of the Holstein Hamiltonian on a square lattice, a canonical system for electron-lattice physics. The resulting ML-enabled large-scale dynamical simulations faithfully capture mesoscale evolution of the symmetry-breaking phase, illustrating the utility of lattice-equivariant architectures for linking microscopic electronic processes to emergent dynamical behavior in condensed-matter lattice systems.

2601.04104Jan 2026

View

Random knotting in very long off-lattice self-avoiding polygons

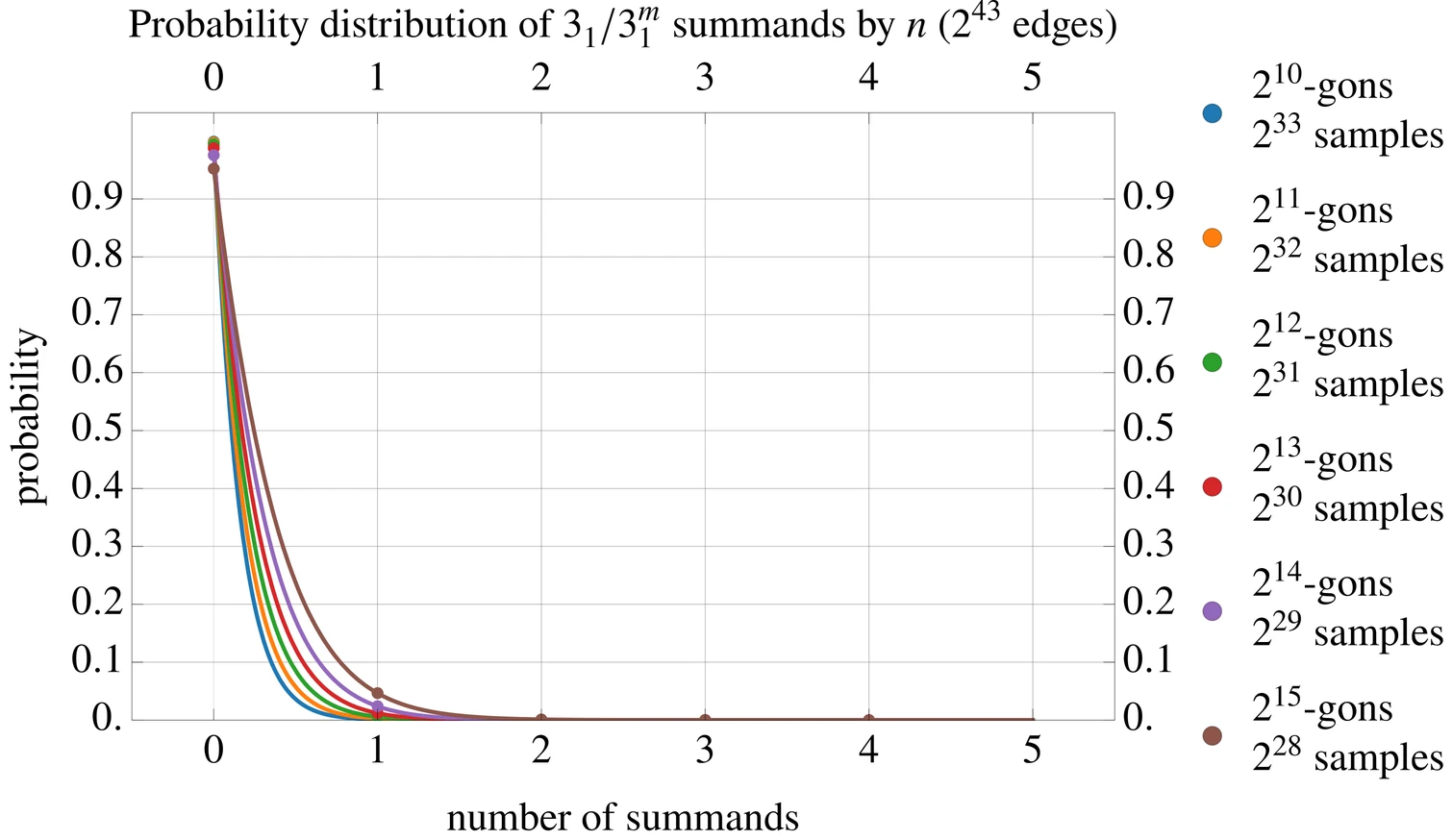
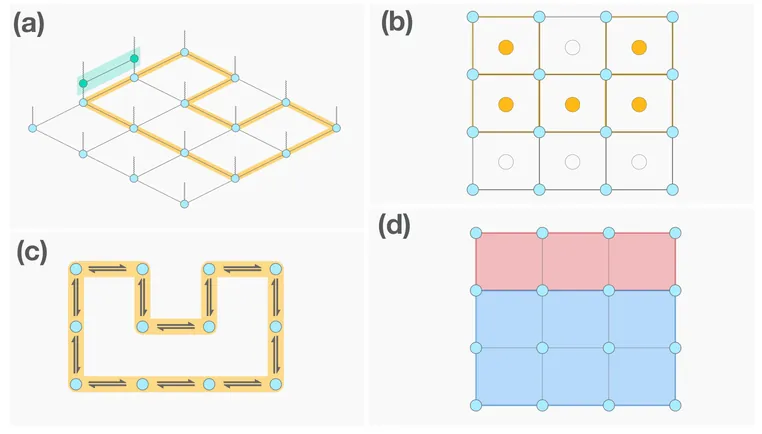
We present experimental results on knotting in off-lattice self-avoiding polygons in the bead-chain model. Using Clisby's tree data structure and the scale-free pivot algorithm, for each $k$ between $10$ and $27$ we generated $2^{43-k}$ polygons of size $n=2^k$. Using a new knot diagram simplification and invariant-free knot classification code, we were able to determine the precise knot type of each polygon. The results show that the number of prime summands of knot type $K$ in a random $n$-gon is very well described by a Poisson distribution. We estimate the characteristic length of knotting as $656500 \pm 2500$. We use the count of summands for large $n$ to measure knotting rates and amplitude ratios of knot probabilities more accurately than previous experiments. Our calculations agree quite well with previous on-lattice computations, and support both knot localization and the knot entropy conjecture.

2601.04102Jan 2026

View

Counterexamples to the conjectured ordering between the waiting-time bound and the thermodynamic uncertainty bound on entropy production

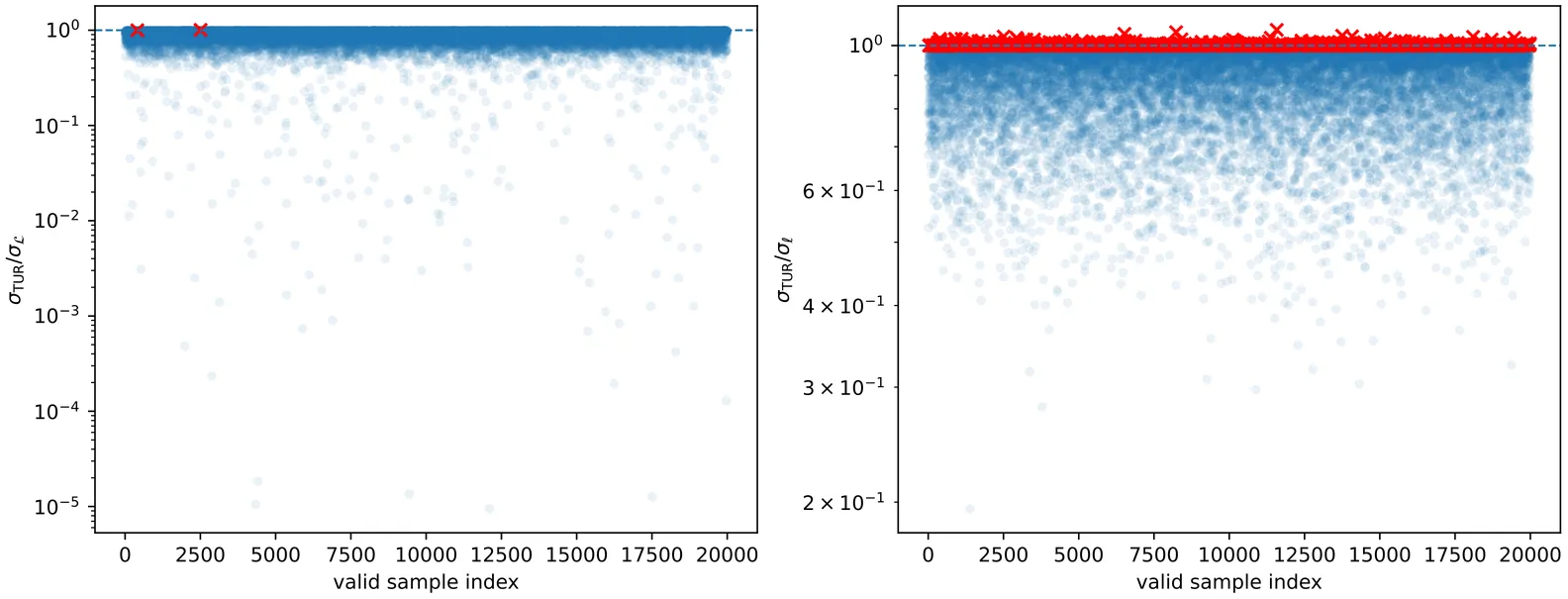
Two widely used model-free lower bounds on the steady-state entropy production rate of a continuous-time Markov jump process are the thermodynamic uncertainty relation (TUR) bound $σ_\text{TUR}$, derived from the mean and variance of a current, and the waiting-time distribution (WTD) bound $σ_\mathcal{L}$, derived from the irreversibility of partially observed transition sequences together with their waiting times. It has been conjectured that $σ_{\mathcal L}$ is always at least as tight as $σ_{\mathrm{TUR}}$ when both are constructed from the same partially observed link. Here we provide four-state counterexamples in a nonequilibrium steady state where $σ_{\mathcal L}<σ_{\mathrm{TUR}}$. This result shows that no universal ordering exists between these two inference bounds under partial observation.

2601.04039Jan 2026

View

Conveyor-mode electron shuttling through a T-junction in Si/SiGe

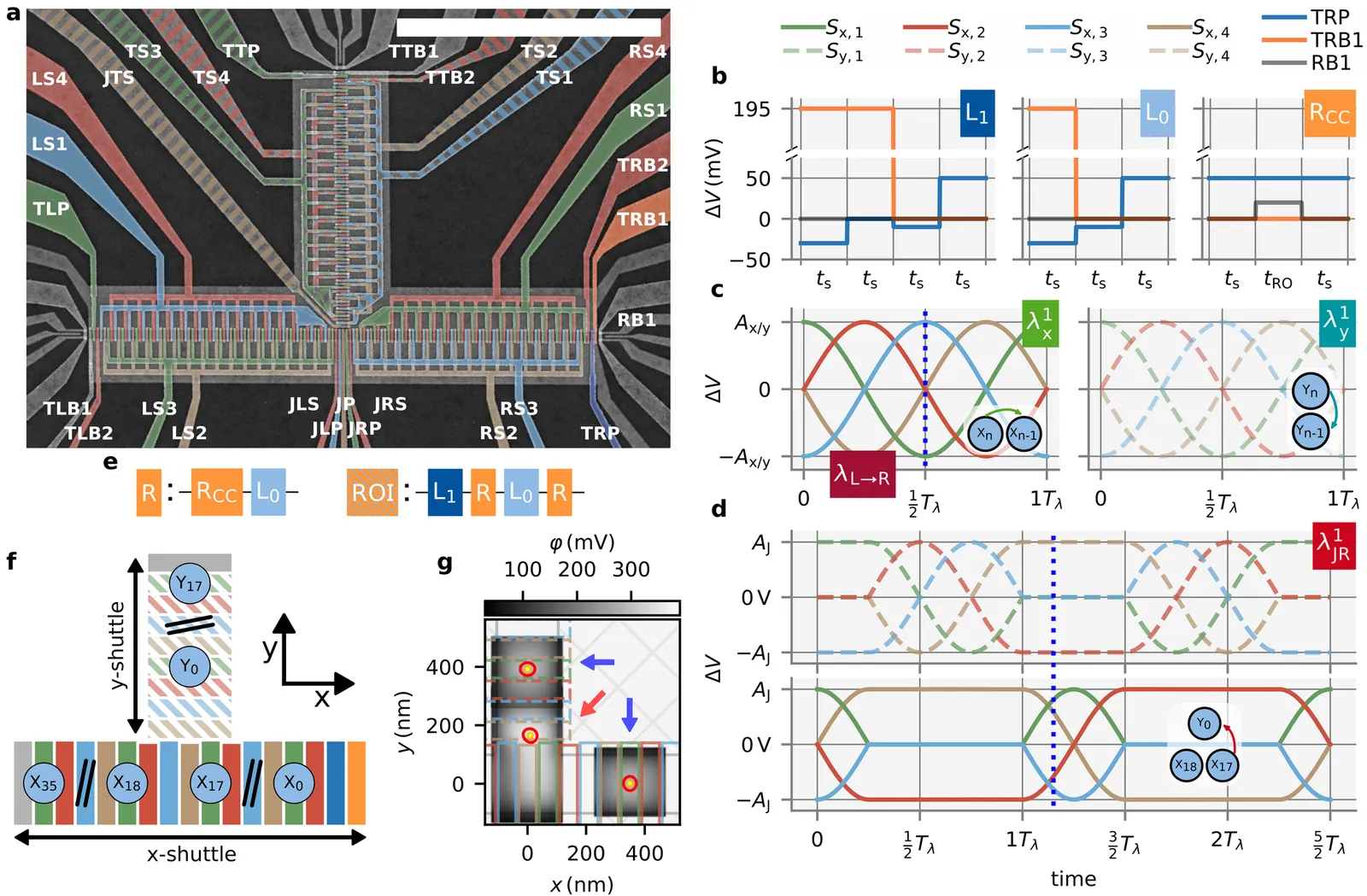
Conveyor-mode shuttling in gated Si/SiGe devices enables adiabatic transfer of single electrons, electron patterns and spin qubits confined in quantum dots across several microns with a scalable number of signal lines. To realize their full potential, linear shuttle lanes must connect into a two-dimensional grid with controllable routing. We introduce a T-junction device linking two independently driven shuttle lanes. Electron routing across the junction requires no extra control lines beyond the four channels per conveyor belt. We measure an inter-lane charge transfer fidelity of $F = 100.0000000^{+0}_{-9\times 10^{-7}}\,\%$ at an instantaneous electron velocity of $270\,\mathrm{mm}\,\mathrm{s}^{-1}$. The filling of 54 quantum dots is controlled by simple atomic pulses, allowing us to swap electron patterns, laying the groundwork for a native spin-qubit SWAP gate. This T-junction establishes a path towards scalable, two-dimensional quantum computing architectures with flexible spin qubit routing for quantum error correction.

2601.039421Jan 2026

View

Layer Hall effect induced by altermagnetism

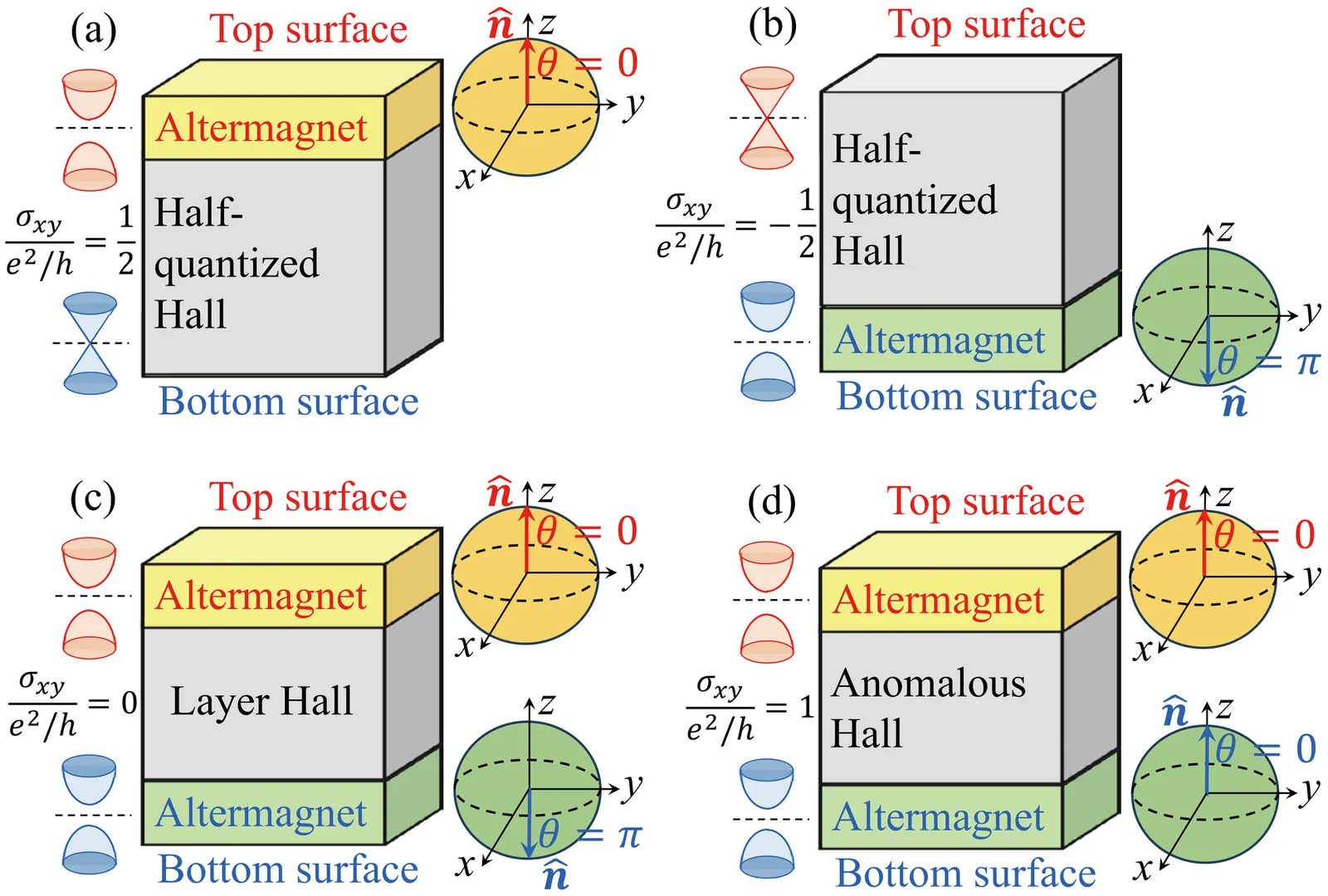
In this work, we propose a scheme to realize the layer Hall effect in the ferromagnetic topological insulator Bi$_2$Se$_3$ via proximity to $d$-wave altermagnets. We show that an altermagnet and an in-plane magnetic field applied near one surface gap the corresponding Dirac cone, yielding an altermagnet-induced half-quantized Hall effect. When altermagnets with antiparallel Néel vectors are placed near the top and bottom surfaces, giving rise to the layer Hall effect with vanishing net Hall conductance, i.e., the altermagnet-induced layer Hall effect. In contrast, altermagnets with parallel Néel vectors lead to a quantized Chern insulating state, i.e., the altermagnet-induced anomalous Hall effect. We further analyze the dependence of the Hall conductance on the orientation of the in-plane magnetic field and demonstrate that the layer Hall effect becomes observable under a perpendicular electric field. Our results establish a route to engineer altermagnet-induced topological phases in ferromagnetic topological insulators.

2601.03937Jan 2026

View

In-plane ferromagnetism-driven topological nodal-point superconductivity with tilted Weyl cones

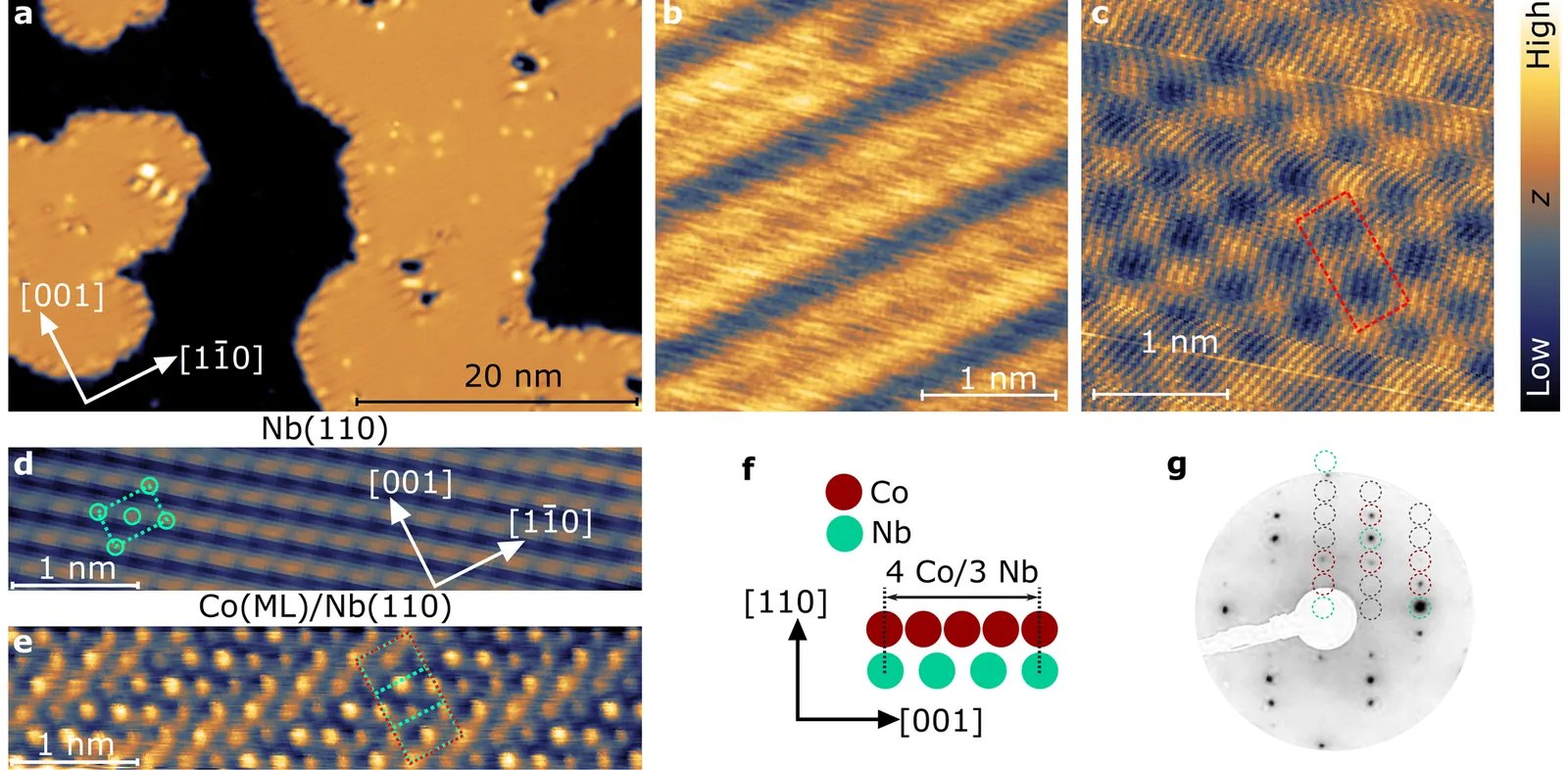
The potential application of topological superconductivity in quantum transport and quantum information has fueled an intense investigation of hybrid materials with emergent electronic properties, including magnet-superconductor heterostructures. Here, we report evidence of a topological nodal-point superconducting phase in a one-atom-thick in-plane ferromagnet in direct proximity to a conventional $s$-wave superconductor. Low-temperature scanning tunneling spectroscopy data reveal the presence of a double-peak low-energy feature in the local density of states of the hybrid system, which is rationalized via model calculations to be an emergent topological nodal-point superconducting phase with tilted Weyl cones. Our results further establish the combination of in-plane ferromagnetism and conventional superconductivity as a route to design two-dimensional topological quantum phases.

2601.03929Jan 2026

View

A current source with metrological precision made on a 300mm silicon MOS process

Although the measurement of current is now defined with respect to the electronic charge, producing a current standard based on a single-electron source remains challenging. The error rate of a source must be below 0.01 ppm, and many such sources must be operated in parallel to provide practically useful values of current in the nanoampere range. Achieving a single electron source using an industrial grade 300 mm wafer silicon metal oxide semiconductor (MOS) process could offer a powerful route for scaling, combined with the ability for integration with control and measurement electronics. Here, we present measurements of such a single-electron source indicating an error rate of 0.008 ppm, below the error threshold to satisfy the SI Ampere, and one of the lowest error rates reported, implemented using a gate-defined quantum dot device fabricated on an industry-grade silicon MOS process. Further evidence supporting the accuracy of the device is obtained by comparing the device performance to established models of quantum tunnelling, which reveal the mechanism of operation of our source at the single particle level. The low error rate observed in this device motivates the development of scaled arrays of parallel sources utilising Si MOS devices to realise a new generation of metrologically accurate current standards.

2601.03916Jan 2026

View

Quantum Otto heat-engine with Kitaev-Heisenberg cluster: Possible roles of frustration, magnons, and duality

We study the performance of Kitaev-Heisenberg (KH) clusters as working media realizing a quantum Otto engine (QOE). An external Zeeman field with linear time dependency is used as the driving mechanism. The efficiency strongly depends on Kitaev ($κ$) and Heisenberg ($J$) exchange interaction. Interestingly, efficiency is comparable when the relative magnitude of $κ$ and $J$ is the same but of opposite signs. The above results are explained due to a subtle interplay of frustration, quantum fluctuation, and duality of eigen-spectra for the KH system when both the signs of $κ$ and $J$ are reversed. The maximum efficiency is shown to be dynamically related to eigen-spectra forming discrete narrow bands, where total spin angular momentum becomes a good quantum number. We relate this optimum efficiency to the realization of weakly interacting magnons, where the system reduces to an approximate eigen-system of the external drive. Finally, we extend our study to the large spin Kitaev model and find a quantum advantage in efficiency for $S=1/2$. The results could be of practical interest for materials with KH interactions as a platform for QOE.

2601.03826Jan 2026

View

Koopman Nonlinear Non-Hermitian Skin Effect

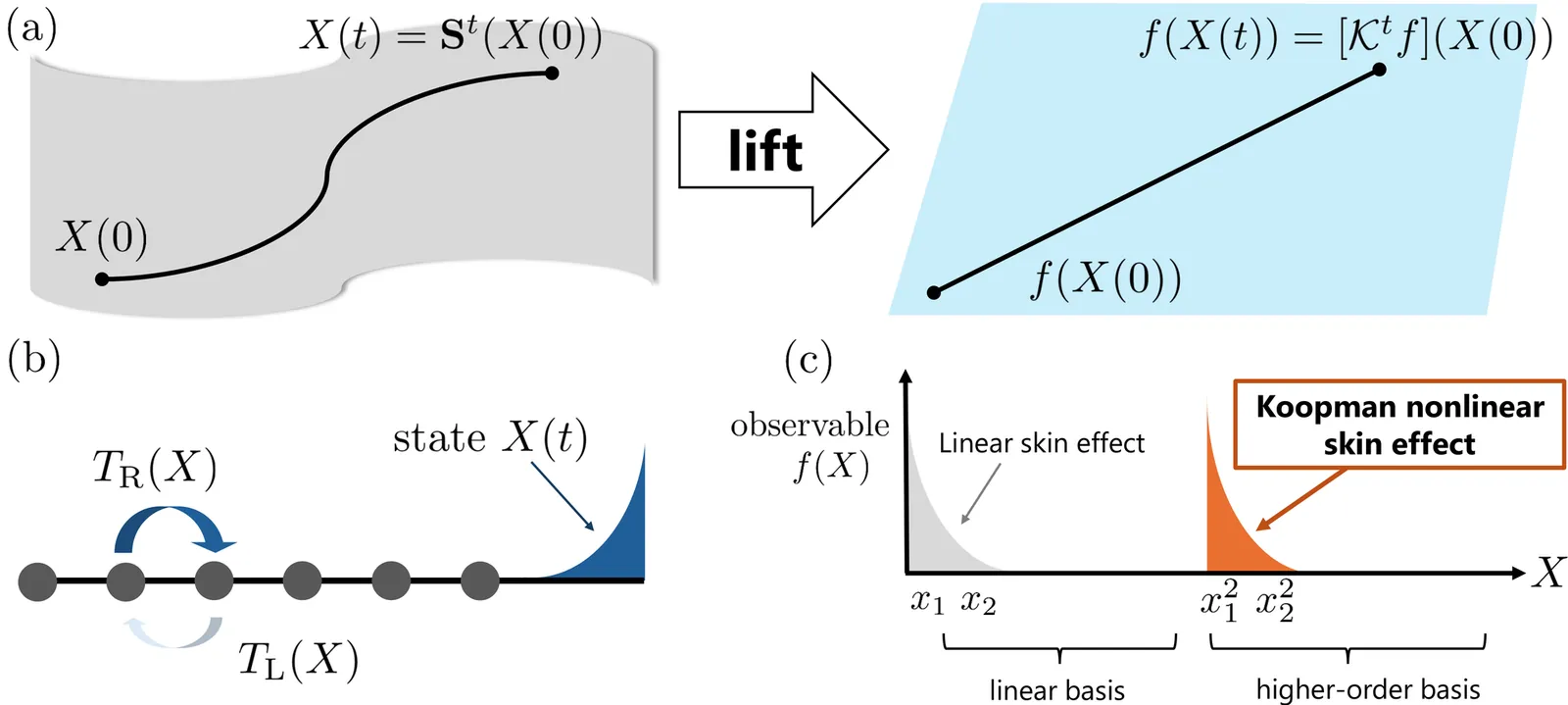
Non-Hermitian skin effects are conventionally manifested as boundary localization of eigenstates in linear systems. In nonlinear settings, however, where eigenstates are no longer well defined, it becomes unclear how skin effects should be faithfully characterized. Here, we propose a Koopman-based characterization of nonlinear skin effects, in which localization is defined in terms of Koopman eigenfunctions in a lifted observable space, rather than physical states. Using a minimal nonlinear extension of the Hatano-Nelson model, we show that dominant Koopman eigenfunctions localize sharply on higher-order observables, in stark contrast to linear skin effects confined to linear observables. This lifted-space localization governs the sensitivity to boundary amplitude perturbations, providing a distinct dynamical signature of the nonlinear skin effect. Our results establish the Koopman framework as a natural setting in which skin effects unique to nonlinear non-Hermitian systems can be identified.

2601.03636Jan 2026

View

Interplay of activity and non-reciprocity in tracer dynamics: From non-equilibrium fluctuation-dissipation to giant diffusion

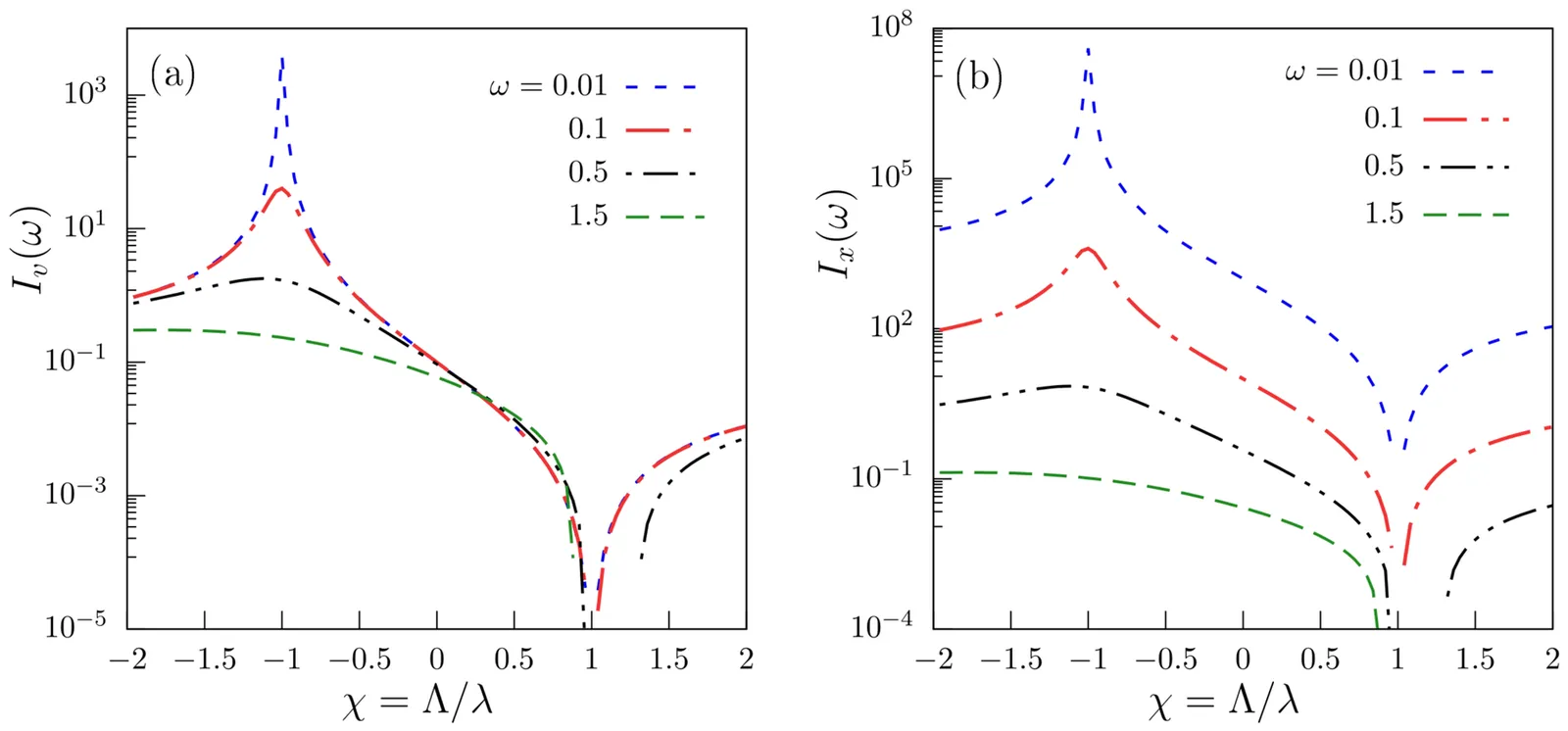
Non-reciprocal interactions play a key role in shaping transport in active and passive systems, giving rise to striking nonequilibrium behavior. Here, we study the dynamics of a tracer -- active or passive -- embedded in a bath of active or passive particles, coupled through non-reciprocal interactions. Starting from the microscopic stochastic dynamics of the full system, we derive an overdamped generalized Langevin equation for the tracer, incorporating a non-Markovian memory kernel that captures bath-mediated correlations. This framework enables us to compute the tracer's velocity and displacement response, derive a generalized nonequilibrium fluctuation-dissipation relation that quantifies deviations from equilibrium behavior, and determine the mean-squared displacement (MSD). We find that while the MSD becomes asymptotically diffusive, the effective diffusivity depends non-monotonically on the degree of non-reciprocity and diverges at an intermediate value. This regime of giant diffusivity provides a generic mechanism for enhanced transport in active soft matter and has direct implications for biological systems exhibiting chase-and-run or predator-prey interactions. Our analytical predictions are supported by numerical simulations of active Brownian particles, highlighting experimentally accessible signatures of non-reciprocal interactions in soft matter.

2601.03591Jan 2026

View

2601.03583

Comments on the formula to extract current-induced torques from the harmonic Hall voltage measurements

We examine the formulas commonly used to estimate current-induced spin-orbit torques from harmonic Hall voltage measurements. In particular, we focus on the factor of two discrepancy among expressions employed to fit harmonic Hall signals measured under an in-plane rotating magnetic field. By explicitly deriving the relevant relations, we clarify the origin of this discrepancy and present the correct form of the fitting formula. We further discuss the determination of the sign of the field-like torque from harmonic Hall voltage measurements, which depends on the assumed form of the current-induced torques.

2601.03583Jan 2026

View

The emergence of net chirality in two-dimensional Dirac fermions system with altermagnetic mass

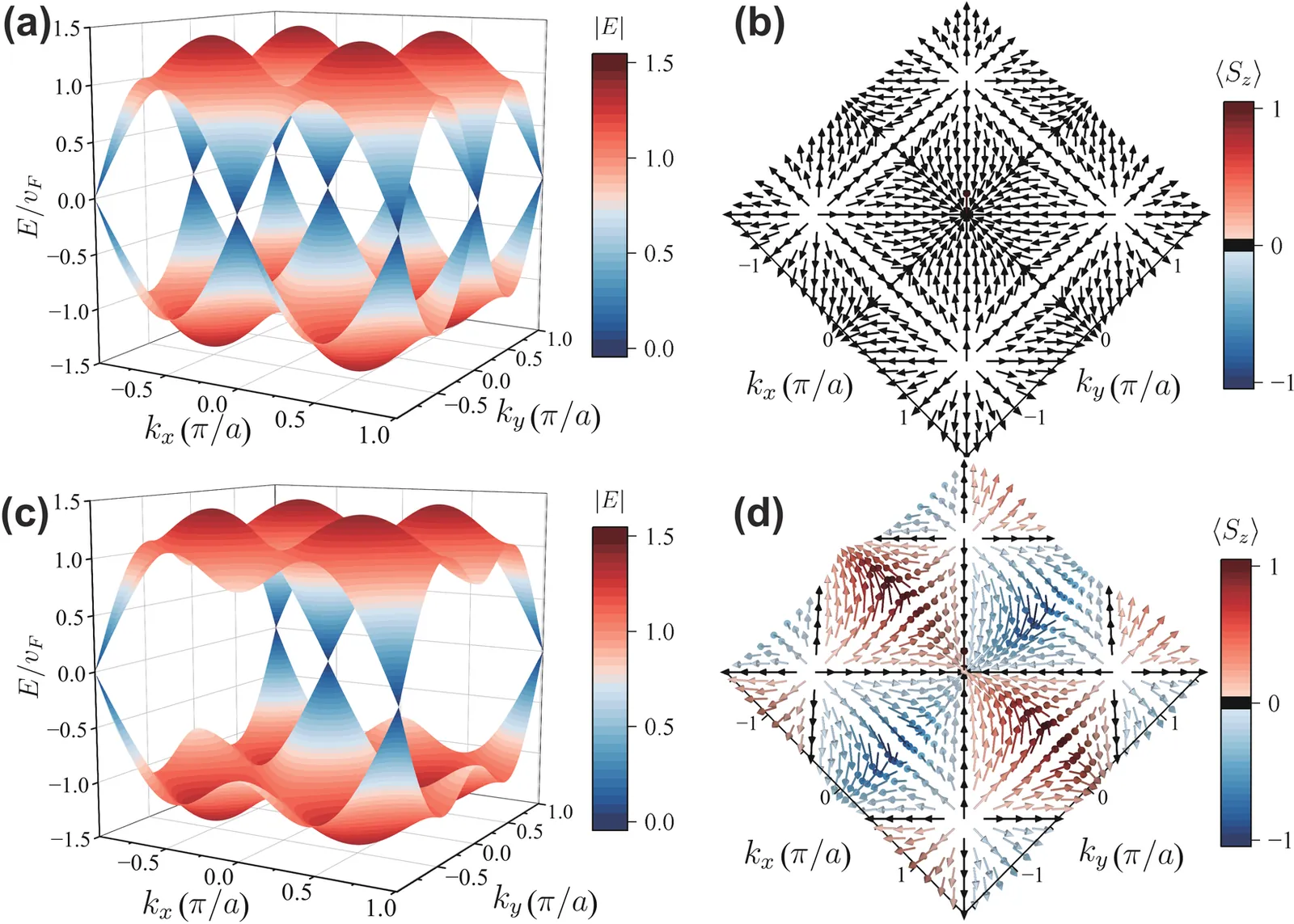
In two-dimensional lattice systems, massless Dirac fermions undergo doubling, leading to the cancellation of net chirality. We demonstrate that the recently discovered altermagnetism can induce a unique mass term, the altermagnetic mass term, which gaps out Dirac cones with one chirality while maintaining the other gapless, leading to the emergence of net chirality. The surviving gapless Dirac cones retain identical winding numbers and exhibit the quantum anomalous Hall effect in the presence of the trivial constant mass term. When subjected to an external magnetic field, the altermagnetic mass induces Landau level asymmetry in Dirac fermions, resulting in fully valley-polarized quantum Hall edge states. Our findings reveal that Dirac fermions with the altermagnetic mass harbor rich physical phenomena warranting further exploration.

2601.03564Jan 2026

View

Wigner solid or Anderson solid -- 2D electrons in strong disorder

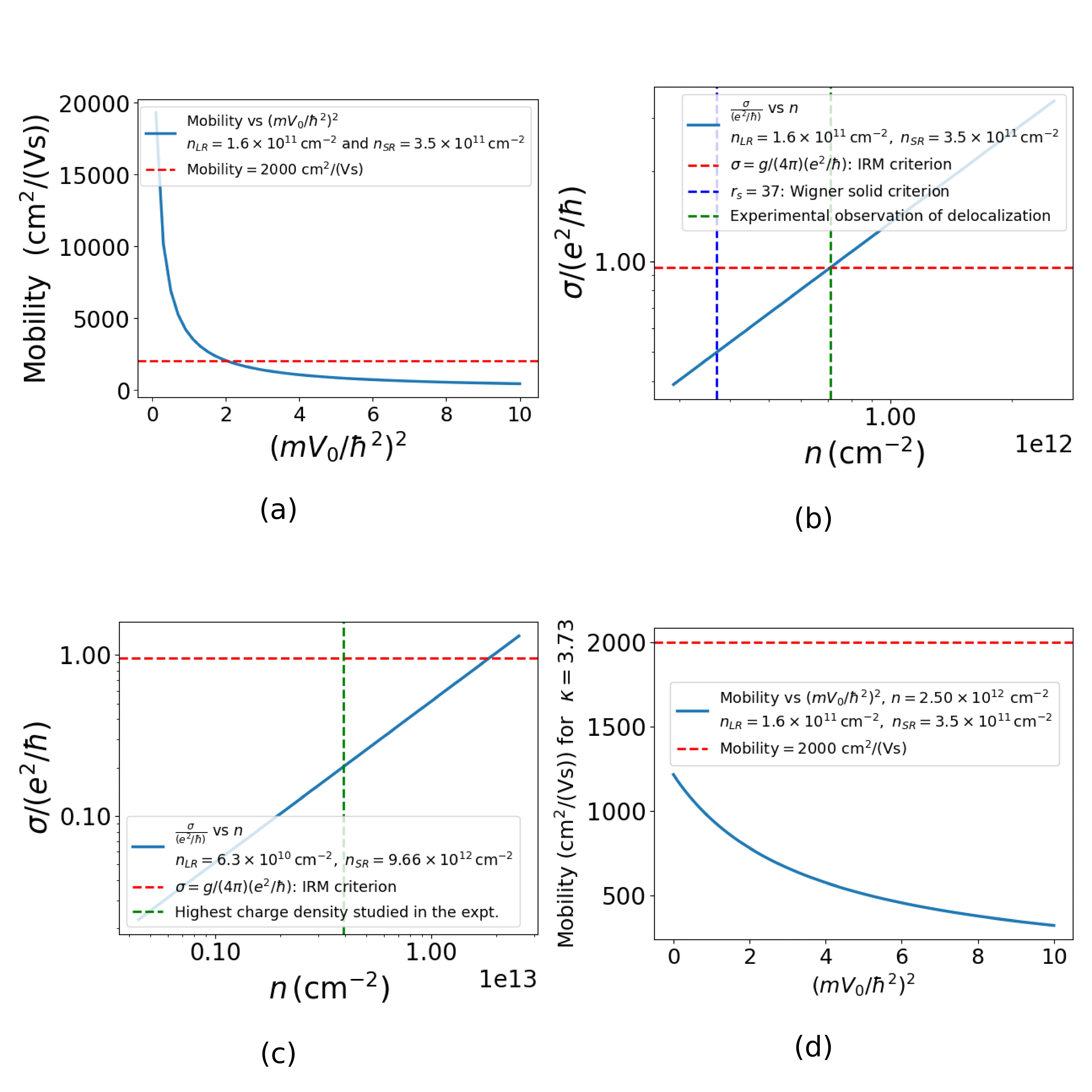
Critically analyzing recent STM and transport experiments [Z. Ge, et al, arXiv:2510.12009] on 2D electron systems in the presence of random quenched impurities, we argue that the resulting low-density putative "solid" phase reported experimentally is better described as an Anderson solid with the carriers randomly spatially localized by impurities than as a Wigner solid where the carriers form a crystal due to an interaction-induced spontaneous breaking of the translational symmetry. In strongly disordered systems, the resulting solid is amorphous, which is adiabatically connected to the infinite disorder Anderson fixed point rather than the zero disorder Wigner crystal fixed point.

2601.03521Jan 2026

View

Optical Spectroscopy of Waveguide coupled Er$^{3+}$ ensembles in CaWO$_4$ and YVO$_4$

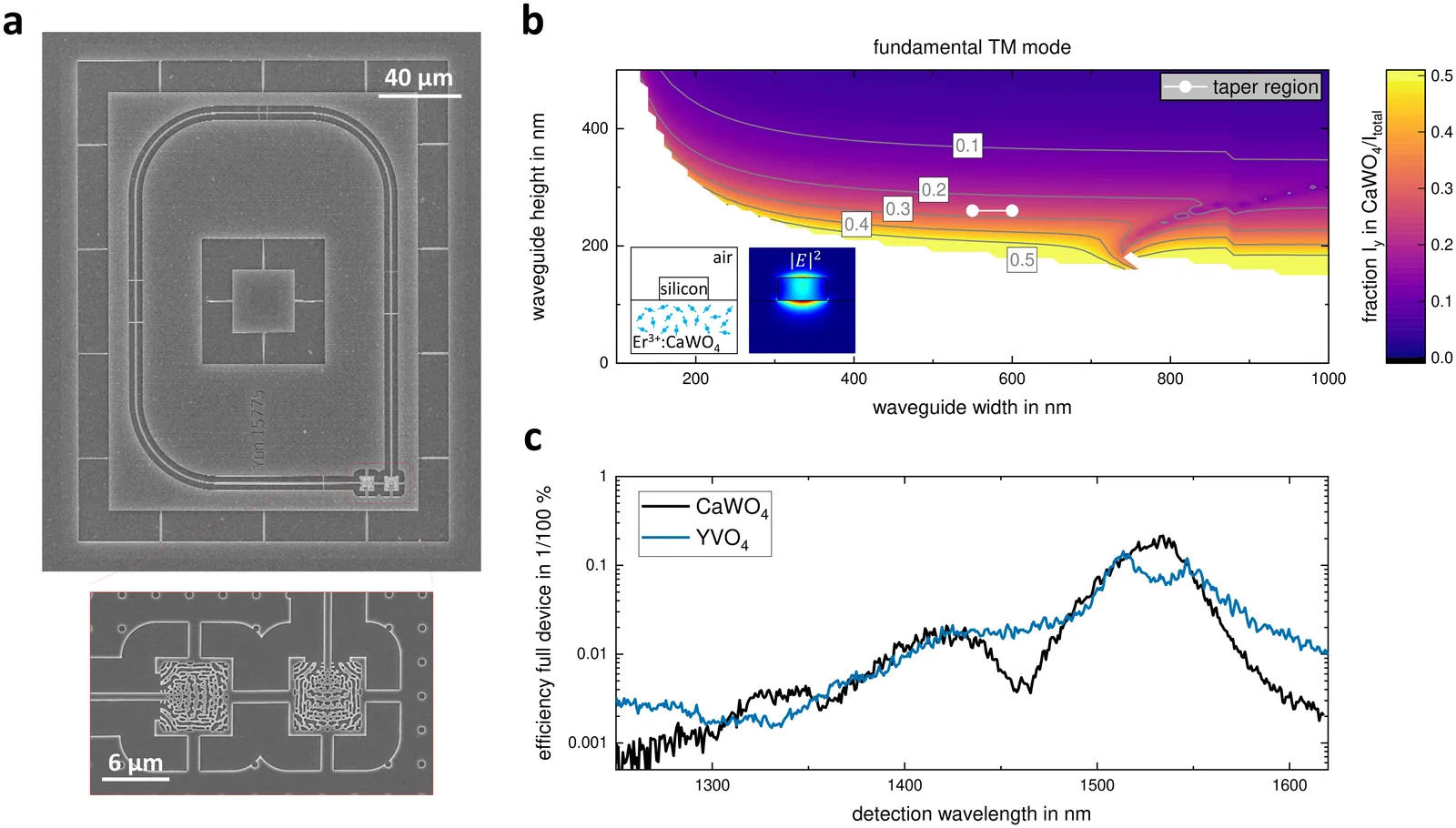
We present an optical study of near-surface Er$^{3+}$ ensembles in waveguide-integrated CaWO$_4$ and YVO$_4$, investigating how nanophotonic coupling modifies rare-earth spectroscopy. In particular, we compare bulk excitation with evanescently coupled TE and TM waveguide modes. In Er$^{3+}$:CaWO$_4$, we observe a pronounced polarization-dependent surface effect. TE-coupled spectra closely reproduce bulk behavior. In contrast, TM coupling induces strong inhomogeneous broadening and an asymmetric low-energy shoulder of the site S1 Y1Z1 transition, with linewidths exceeding those of the bulk by more than a factor of four. Temperature-dependent measurements and surface termination studies indicate that surface charges are the dominant mechanism. Er$^{3+}$:YVO$_4$ remains largely unaffected by mode polarization, and surface termination leads only to minor spectral shifts. These observations suggest that non-charge-neutral rare-earth systems are more susceptible to surface-induced decoherence sources than charge-neutral hosts.

2601.03455Jan 2026

View

The Zubarev Double Time Greens function-A Vintage Many Body Technique

These lecture notes present a comprehensive and powerful many-body technique pioneered in 1960 by D. N. Zubarev. The technique, known as the Zubarev Double Time Greens Function method, was used extensively by leading solid state physicists such as John Hubbard and Laura Roth in the 1960s. We present the technique and apply it to the non-interacting electron and boson gas. We next consider the (many-body) Hubbard model and show how it yields the Stoner criterion for ferromagnetism. It is easily extendable to superconductivity and related problems. Our treatment is pedagogical and understandable to those with just an elementary understanding of second quantization.

2601.03439Jan 2026

View

Altermagnetic Superconducting Diode Effect in Mn$_{3}$Pt/Nb Heterostructures

Compensated magnetic orders that can split the spin-degeneracy of electronic bands have become a very active field of research. As opposed to spin-orbit coupling, the splitting resulting from these "altermagnets" is not a small relativistic correction and, in contrast to ferromagnets, not accompanied by a net magnetization and large stray fields. In particular, the theoretical analysis of the interplay of altermagnetism and superconductivity has taken center stage, while experimental investigations of their coexistence remain in their infancy. We here study heterostructures consisting of Nb thins films interfaced with the $T_1$ and $T_2$ phases of Mn$_3$Pt. These non-collinear magnetic states can be thought of as descendants from the same altermagnetic order in the absence of spin-orbit coupling. We demonstrate the non-trivial impact on the superconducting state of Nb, which exhibits a zero-field superconducting diode effect, despite the compensated ($T_2$) and nearly-compensated ($T_1$) magnetic order; the diode efficiencies can reach large values (up to 50$\%$). The diode effect is found to be highly sensitive to the form of the magnetic order, illustrating its potential as a symmetry probe. The complex magnetic field and temperature dependence hint at a rich interplay of multiple contributing mechanisms. Our results define a new materials paradigm for dissipationless spintronics and magnetization-free diode functionality, while motivating further exploration of non-collinear altermagnetic superconductors.

2601.033661Jan 2026

View

Light-Induced Even-Parity Unidirectional Spin Splitting in Coplanar Antiferromagnets

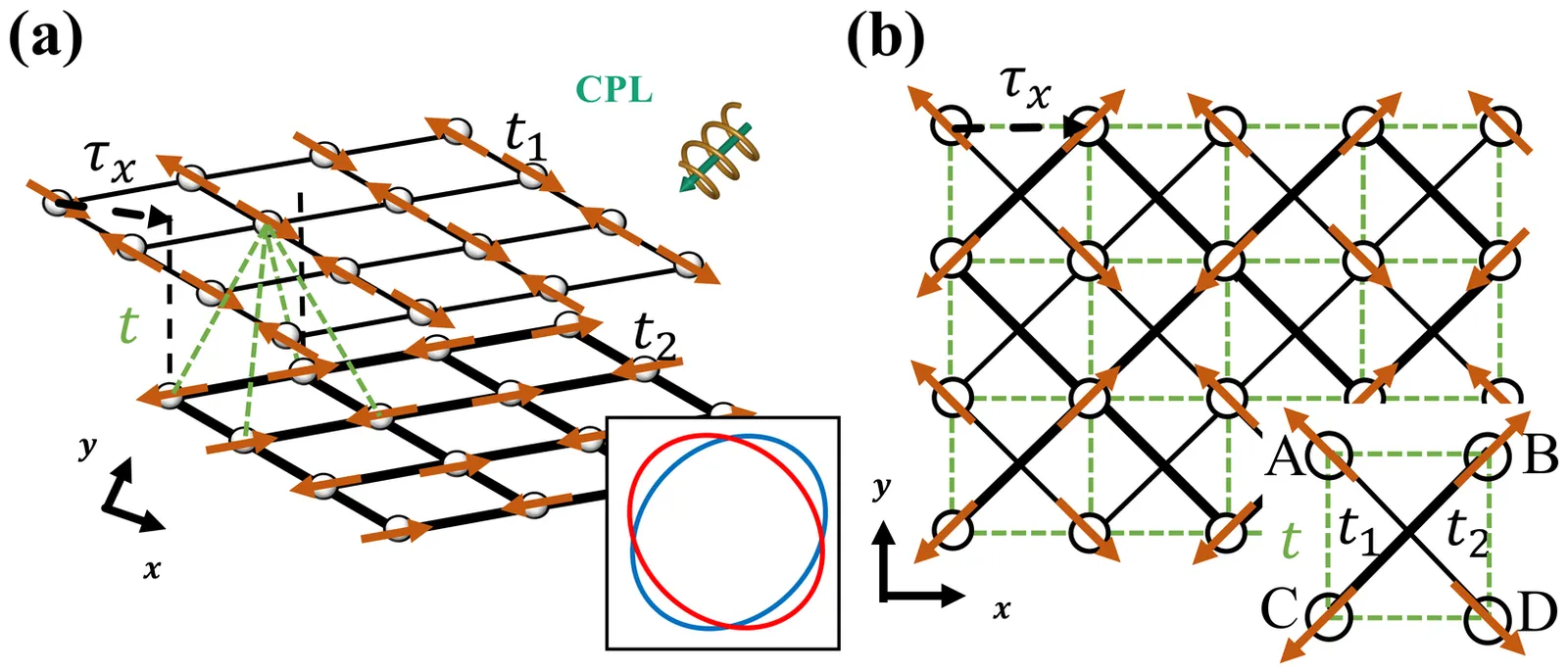
When a coplanar antiferromagnet (AFM) with $xy$-plane magnetic moments exhibits a spin-split band structure and unidirectional spin polarization along $z$, the spin polarization is forced to be an odd function of momentum by the fundamental symmetry $[\bar{C}_{2z}\|\mathcal{T}]$. Coplanar AFMs displaying such odd-parity unidirectional spin splittings are known as odd-parity magnets. In this work, we propose the realization of their missing even-parity counterparts. We begin by deriving the symmetry conditions required for an even-parity, out-of-plane spin splitting. We then show that irradiating a spin-degenerate coplanar AFM with circularly polarized light lifts the $[\bar{C}_{2z}|\mathcal{T}]$ constraint, dynamically generating this even-parity state. Specifically, the light-induced unidirectional spin splitting exhibits a $d$-wave texture in momentum space, akin to that of a $d$-wave altermagnet. We prove this texture's robustness against spin canting and show it yields a unique clover-like angular dependence in the Drude spin conductivity. Our work demonstrates that optical driving can generate novel spin-split phases in coplanar AFMs, thereby diversifying the landscape of materials exhibiting distinct spin splittings.

2601.03358Jan 2026

View

Critical aging and relaxation dynamics in long-range systems

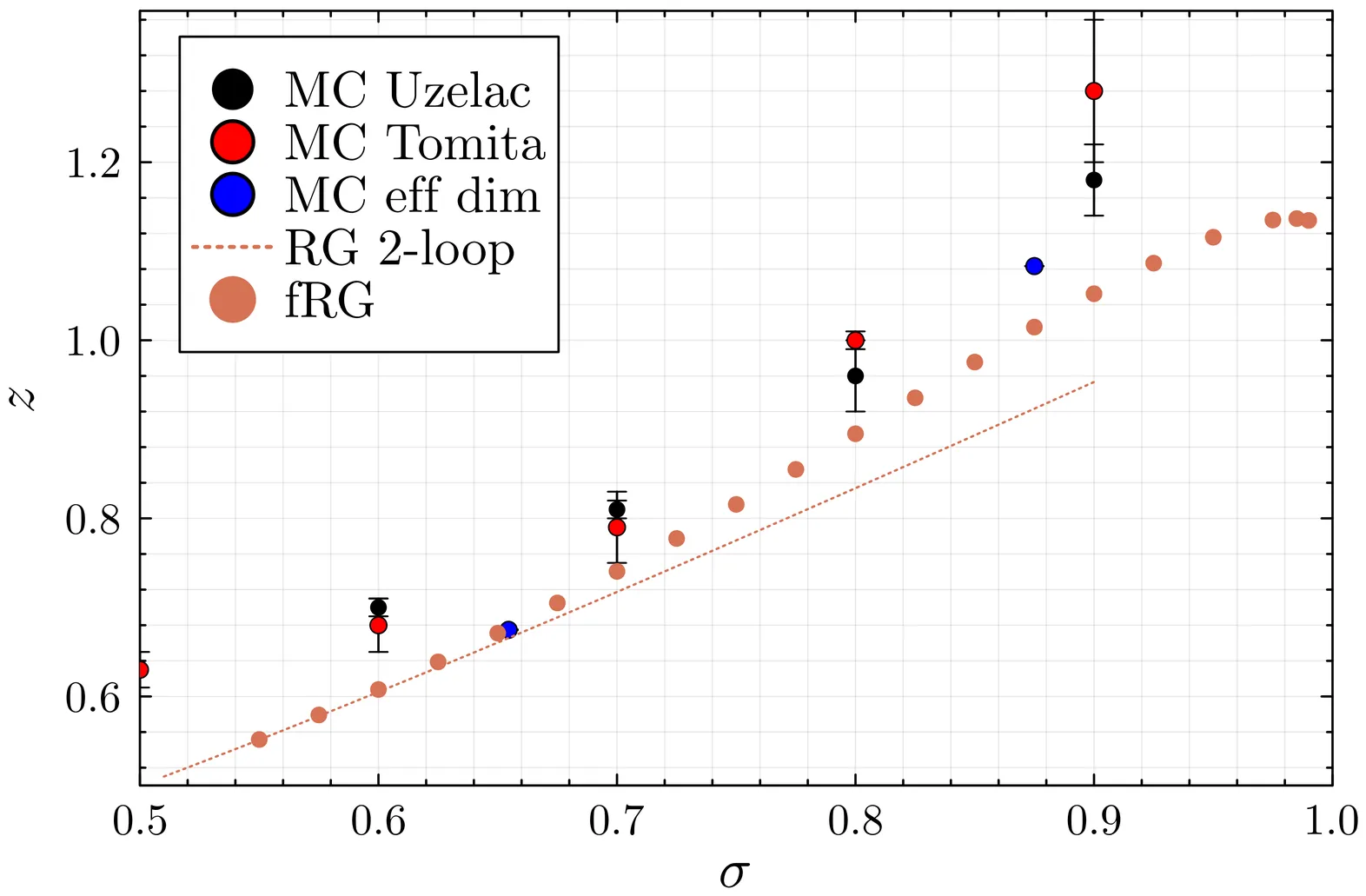
We study the dynamical scaling of long-range $\mathrm{O}(N)$ models after a sudden quench to the critical temperature, using the functional renormalization group approach. We characterize both short-time aging and long-time relaxation as a function of the symmetry index $N$, the interaction range decay exponent $σ$ and the dimension $d$. Our results substantially improve on perturbative predictions, as demonstrated by benchmarks against Monte Carlo simulations and the large-$N$ limit. Finally, we demonstrate that long-range systems increase the performance of critical heat engines with respect to a local active medium.

2601.03355Jan 2026

View

Page 1 of 179