Statistical Mechanics

arXiv:cond-mat.stat-mech

Phase transitions, thermodynamics, field theory, non-equilibrium phenomena, renormalization group, percolation.

Looking for a broader view? This category is part of:

Trending in Statistical Mechanics

Large language models and the entropy of English

We use large language models (LLMs) to uncover long-ranged structure in English texts from a variety of sources. The conditional entropy or code length in many cases continues to decrease with context length at least to $N\sim 10^4$ characters, implying that there are direct dependencies or interactions across these distances. A corollary is that there are small but significant correlations between characters at these separations, as we show from the data independent of models. The distribution of code lengths reveals an emergent certainty about an increasing fraction of characters at large $N$. Over the course of model training, we observe different dynamics at long and short context lengths, suggesting that long-ranged structure is learned only gradually. Our results constrain efforts to build statistical physics models of LLMs or language itself.

2512.24969

Dec 2025Statistical Mechanics

2601.00294

Bridging Commutant and Polynomial Methods for Hilbert Space Fragmentation

A quantum model exhibits Hilbert space fragmentation (HSF) if its Hilbert space decomposes into exponentially many dynamically disconnected subspaces, known as Krylov subspaces. A model may however have different HSFs depending on the method for identifying them. Here we establish a connection between two vastly distinct methods recently proposed for identifying HSF: the commutant algebra (CA) method and integer characteristic polynomial factorization (ICPF) method. For a Hamiltonian consisting of operators admitting rational number matrix representations, we prove a theorem that, if its center of commutant algebra have all eigenvalues being rational, the HSF from the ICPF method must be equal to or finer than that from the CA method. We show that this condition is satisfied by most known models exhibiting HSF, for which we demonstrate the validity of our theorem. We further discuss representative models for which ICPF and CA methods yield different HSFs. Our results may facilitate the exploration of a unified definition of HSF.

2601.00294

Jan 2026Statistical Mechanics

An introduction to monitored quantum systems and quantum trajectories: spectrum, typicality, and phases

Thanks to recent experimental advances in simulating and detecting quantum dynamics with high precision and controllability, our understanding of the physics of monitored quantum systems has considerably deepened over the past decades. In this article, we provide an introductory theoretical review on the basic formalisms governing open quantum dynamics under measurement, along with recent developments in their spectral and typical aspects. After reviewing quantum measurement theory, we introduce the concept of quantum trajectories, which are the conditional dynamics of monitored states shaped by a set of measurement outcomes. We then discuss the spectral properties of the dynamical map describing the evolution averaged over measurement outcomes. As has recently been recognized, these spectral features are intimately connected to whether quantum trajectories exhibit typical behaviors, such as the ergodicity and purification. Moreover, we introduce Lyapunov exponents of typical quantum trajectories and discuss how these quantities serve as indicators of measurement-induced phase transitions in monitored quantum many-body systems.

2512.19922

Dec 2025Statistical Mechanics

Scaling of free cumulants in closed system-bath setups

The Eigenstate Thermalization Hypothesis (ETH) has been established as a cornerstone for understanding thermalization in quantum many-body systems. Recently, there has been growing interest in the full ETH, which extends the framework of the conventional ETH and postulates a smooth function to describe the multi-point correlations among matrix elements. Within this framework, free cumulants play a central role, and most previous studies have primarily focused on closed systems. In this paper, we extend the analysis to a system-bath setup, considering both an idealized case with a random-matrix bath and a more realistic scenario where the bath is modeled as a defect Ising chain. In both cases, we uncover a universal scaling of microcanonical free cumulants of system observables with respect to the interaction strength. Furthermore we establish a connection between this scaling behavior and the thermalization dynamics of the thermal free cumulants of corresponding observables.

2511.113331

Nov 2025Statistical Mechanics

Related categories:

Disordered Systems and Neural Networks Mesoscale and Nanoscale Physics Materials Science Other Condensed Matter Quantum Gases

619 papers

How many-body chaos emerges in the presence of quasiparticles

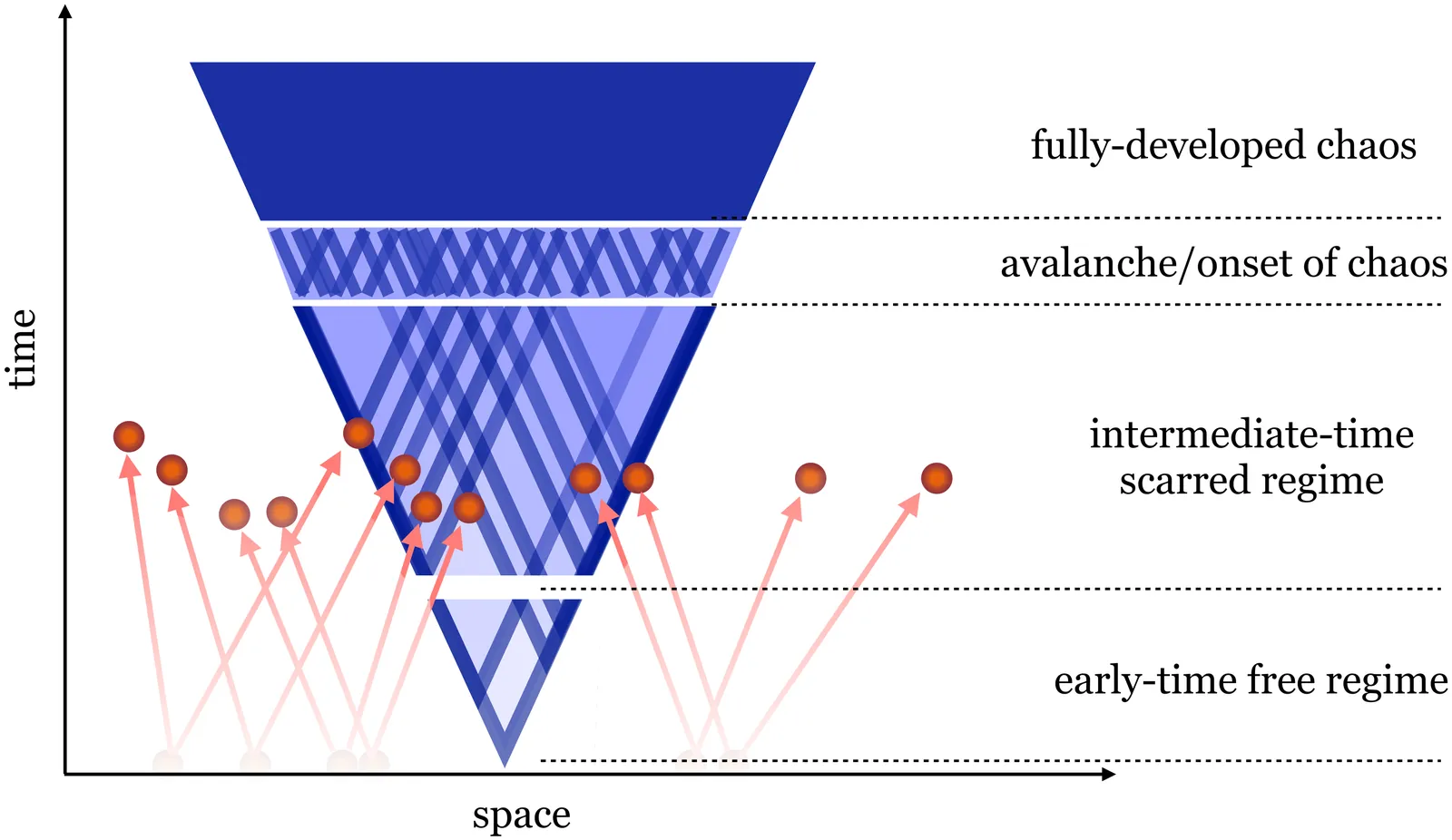
Many-body chaos is a default property of many-body systems; at the same time, near-integrable behaviour due to weakly interacting quasiparticles is ubiquitous throughout condensed matter at low temperature. There must therefore be a, possibly generic, crossover between these very different regimes. Here, we develop a theory encapsulating the notion of a cascade of lightcones seeded by sequences of scattering of weakly interacting harmonic modes as witnessed by a suitably defined chaos diagnostic (classical decorrelator) that measures the spatiotemporal profile of many-body chaos. Our numerics deals with the concrete case of a classical Heisenberg chain, for either sign of the interaction, at low temperatures where the short-time dynamics are well captured in terms of non-interacting spin waves. To model low-temperature dynamics, we use ensembles of initial states with randomly embedded point defects in an otherwise ordered background, which provides a controlled setting for studying the scattering events. The decorrelator exhibits a short-time integrable regime followed by an intermediate `scarred' regime of the cascade of lightcones in progress; these then overlap, leading to an avalanche of scattering events which finally yields the standard long-time signature of many-body chaos.

2601.05238Jan 2026

View

Fluctuation-response relation for a nonequilibrium system with resolved Markovian embedding

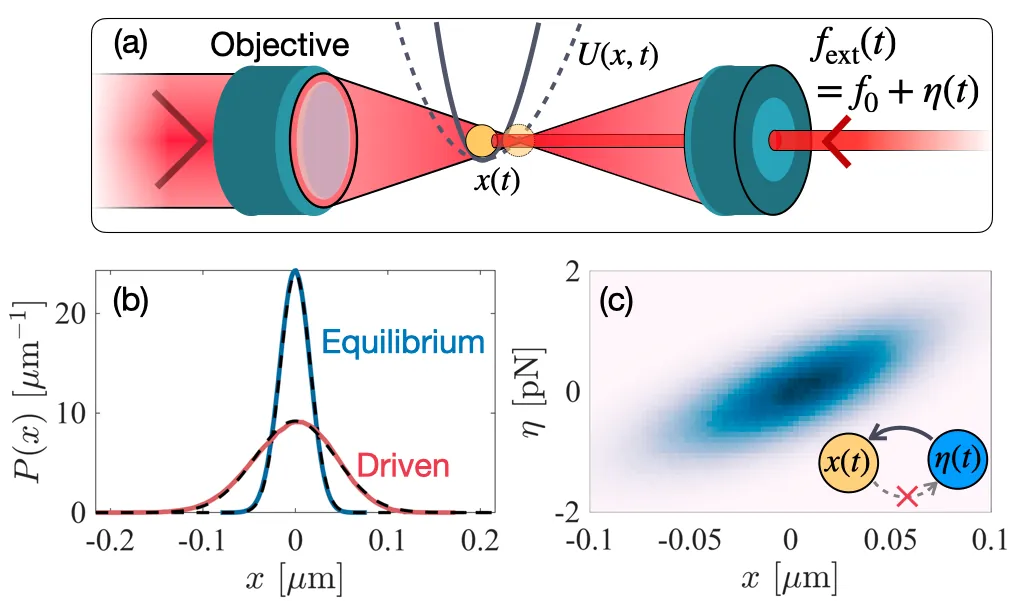
Fluctuation-response relations must be modified to describe nonequilibrium systems with non-Markovian dynamics. Here, we experimentally demonstrate that such relation is quantitatively recovered when the appropriate Markovian embedding of the dynamics is explicitly resolved. Using a colloidal particle optically trapped in a harmonic potential and driven out of equilibrium by a controlled colored noise, we study the response to a perturbation of the stiffness of the confining potential. While the reduced dynamics violates equilibrium fluctuation-response relations, we show that the dynamical response to the stiffness perturbation is fully determined by steady-state correlations involving the exact conjugate observable in the Markovian embedding.

2601.05198Jan 2026

View

Full counting statistics in the sine--Gordon model

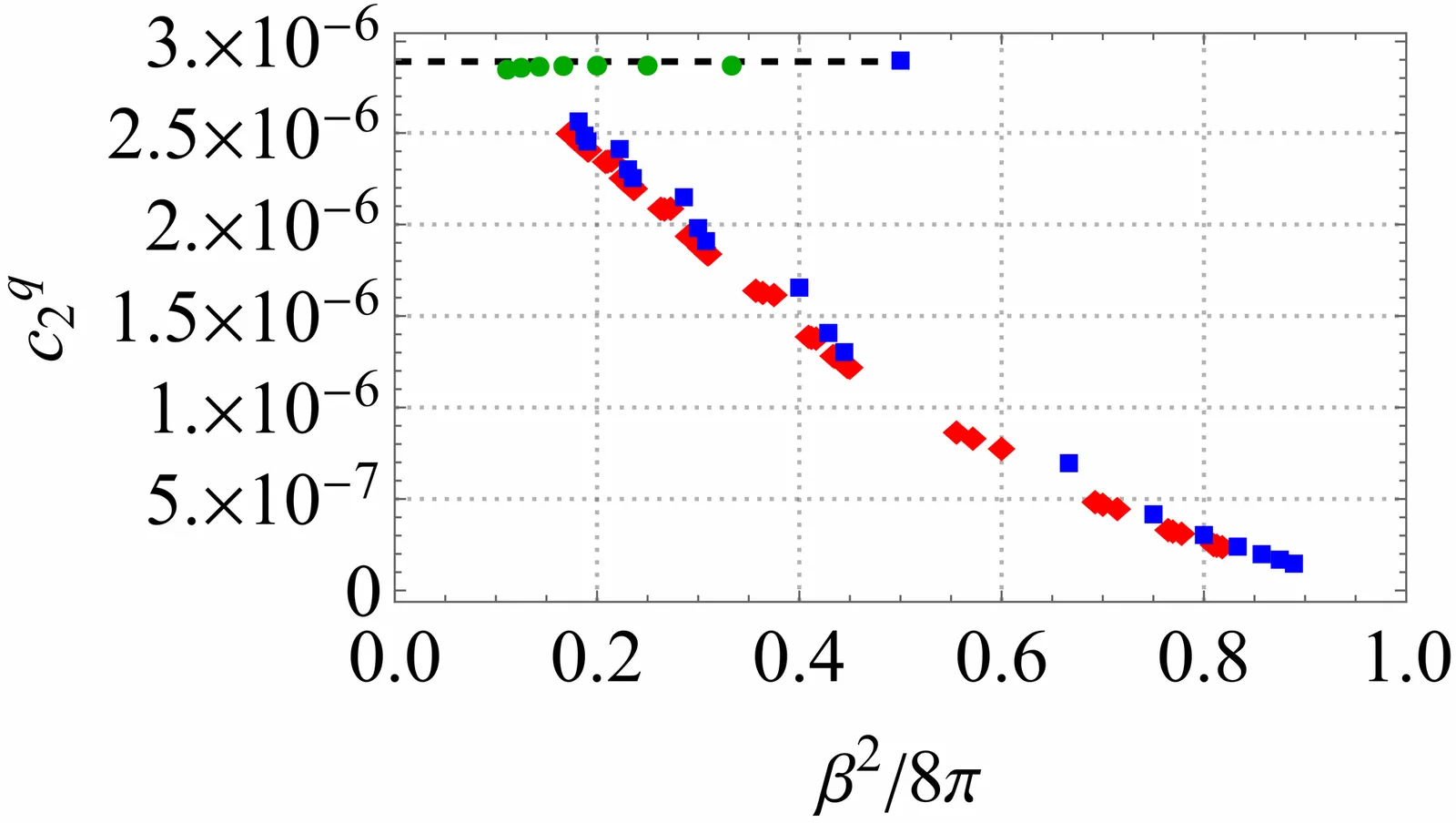
Full counting statistics (FCS) is a dynamical generalisation of the free energy, encapsulating detailed information about the distribution and large-scale correlation functions of conserved charges and their associated currents. In this work, we present a comprehensive numerical study of the FCS and the cumulants of the three lowest charges across the full parameter space of the sine--Gordon field theory. To this end, we extend the thermodynamic Bethe Ansatz (TBA) formulation of the FCS to the sine--Gordon model, emphasise the methodological subtleties for a reliable numerical implementation, and compare numerical results with analytical predictions in certain limits.

2601.05079Jan 2026

View

Microscopic and hydrodynamic correlation in 1d hard rod gas

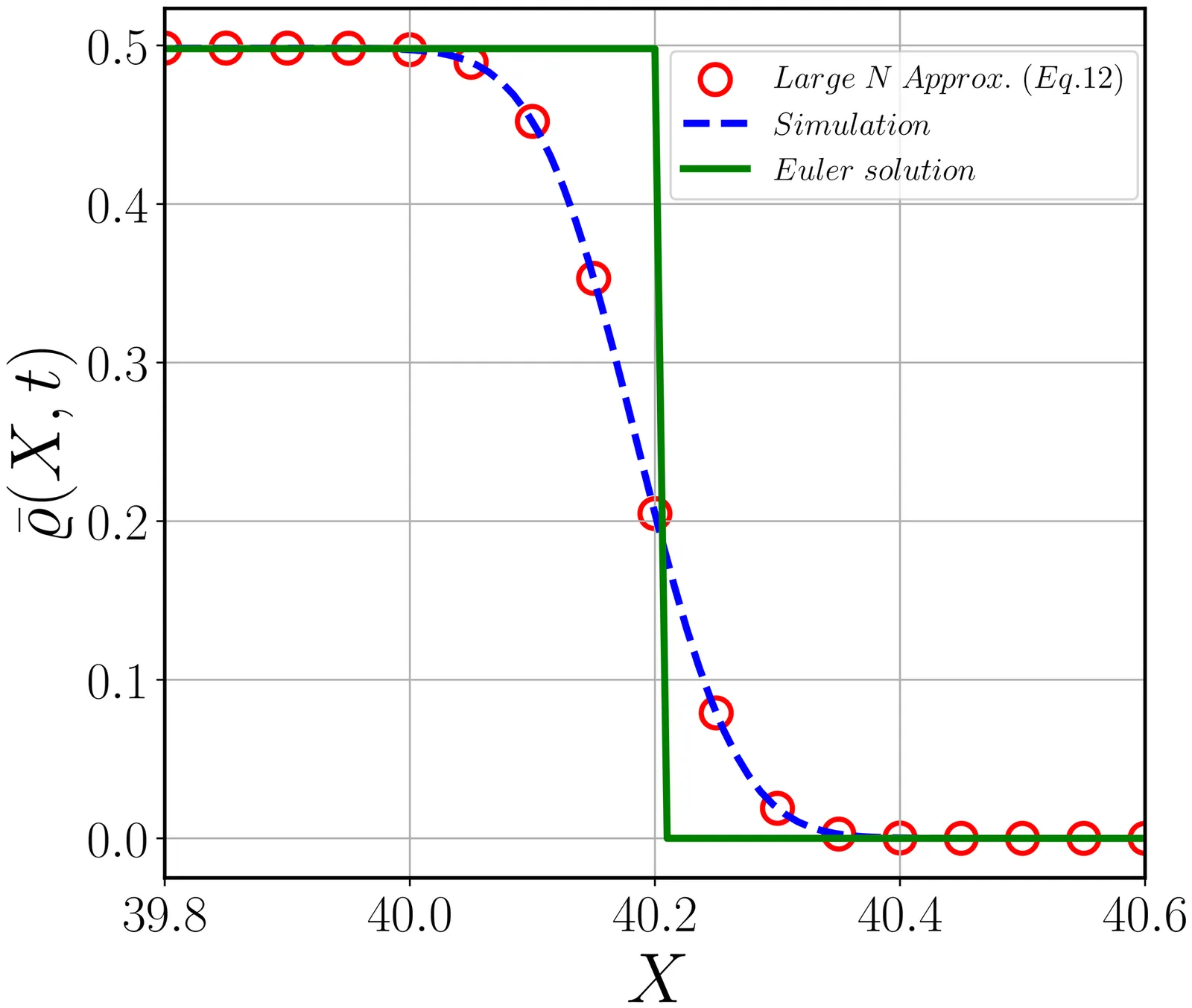
We compute mass density correlations of a one-dimensional gas of hard rods at both microscopic and macroscopic scales. We provide exact analytical calculations of the microscopic correlation. For the correlation at macroscopic scale,, we utilize Ballistic Macroscopic Fluctuation Theory (BMFT) to derive an explicit expression for the correlations of a coarse-grained mass density, which reveals the emergence of long-range correlations on the Euler space-time scale. By performing a systematic coarse-graining of our exact microscopic results, we establish a micro-macro correspondence and demonstrate that the resulting macroscopic correlations agree precisely with the predictions of BMFT. This analytical verification provides a concrete validation of the underlying assumptions of hydrodynamic theory in the context of hard rod gas.

2601.04951Jan 2026

View

Short-time statistics of extinction and blowup in reaction kinetics

We study the statistics of extinction and blowup times in well-mixed systems of stochastically reacting particles. We focus on the short-time tail, $T \to 0$, of the extinction- or blowup-time distribution $\mathcal{P}_m(T)$, where $m$ is the number of particles at $t=0$. This tail often exhibits an essential singularity at $T=0$, and we show that the singularity is captured by a time-dependent WKB (Wentzel-Kramers-Brillouin) approximation applied directly to the master equation. This approximation, however, leaves undetermined a large pre-exponential factor. Here we show how to calculate this factor by applying a leading- and a subleading-order WKB approximation to the Laplace-transformed backward master equation. Accurate asymptotic results can be obtained when this WKB solution can be matched to another approximate solution (the ``inner" solution), valid for not too large $m$. We demonstrate and verify this method on three examples of reactions which are also solvable without approximations.

2601.04924Jan 2026

View

2601.04640

Construction of asymptotic quantum many-body scar states in the SU($N$) Hubbard model

We construct asymptotic quantum many-body scars (AQMBS) in one-dimensional SU($N$) Hubbard chains ($N\geq 3$) by embedding the scar subspace into an auxiliary Hilbert subspace $\mathcal{H}_P$ and identifying a parent Hamiltonian within it, together with a corresponding extension of the restricted spectrum-generating algebra to the multi-ladder case. Unlike previous applications of the parent-Hamiltonian scheme, we show that the parent Hamiltonian becomes the SU($N$) ferromagnetic Heisenberg model rather than the spin-1/2 case, so that its gapless magnons realize explicit AQMBS of the original model. Working in the doublon-holon subspace, we derive this mapping, obtain the one-magnon dispersion for periodic and open boundaries, and prove (i) orthogonality to the tower of scar states, (ii) vanishing energy variance in the thermodynamic limit, and (iii) subvolume entanglement entropy with rigorous MPS/MPO bounds. Our results broaden the parent-Hamiltonian family for AQMBS beyond spin-1/2 and provide analytic, low-entanglement excitations in SU($N$)-symmetric systems.

2601.04640Jan 2026

View

Energy-Time-Accuracy Tradeoffs in Thermodynamic Computing

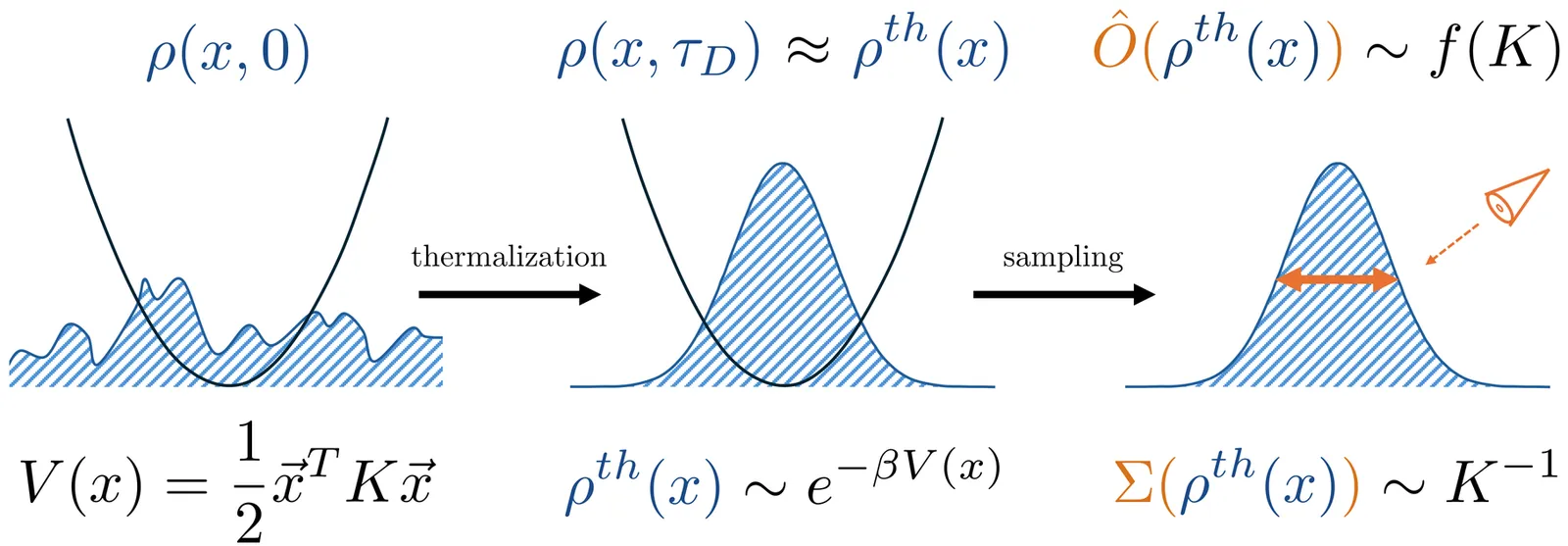
In the paradigm of thermodynamic computing, instead of behaving deterministically, hardware undergoes a stochastic process in order to sample from a distribution of interest. While it has been hypothesized that thermodynamic computers may achieve better energy efficiency and performance, a theoretical characterization of the resource cost of thermodynamic computations is still lacking. Here, we analyze the fundamental trade-offs between computational accuracy, energy dissipation, and time in thermodynamic computing. Using geometric bounds on entropy production, we derive general limits on the energy-delay-deficiency product (EDDP), a stochastic generalization of the traditional energy-delay product (EDP). While these limits can in principle be saturated, the corresponding optimal driving protocols require full knowledge of the final equilibrium distribution, i.e., the solution itself. To overcome this limitation, we develop quasi-optimal control schemes that require no prior information of the solution and demonstrate their performance for matrix inversion in overdamped quadratic systems. The derived bounds extend beyond this setting to more general potentials, being directly relevant to recent proposals based on non-equilibrium Langevin dynamics.

2601.04358Jan 2026

View

Stochastic Path Compression for Spectral Tensor Networks on Cyclic Graphs

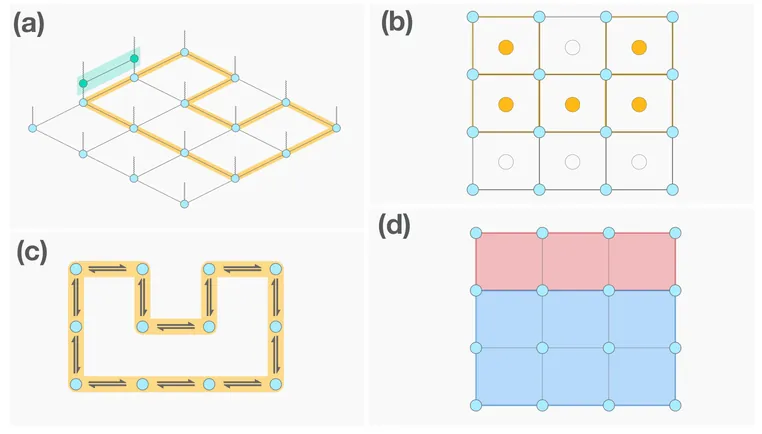
We develop a new approach to compress cyclic tensor networks called stochastic path compression (SPC) that uses an iterative importance sampling procedure to target edges with large bond-dimensions. Closed random walks in SPC form compression pathways that spatially localize large bond-dimensions in the tensor network. Analogous to the phase separation of two immiscible liquids, SPC separates the graph of bond-dimensions into spatially distinct high and low density regions. When combined with our integral decimation algorithm, SPC facilitates the accurate compression of cyclic tensor networks with continuous degrees of freedom. To benchmark and illustrate the methods, we compute the absolute thermodynamics of $q$-state clock models on two-dimensional square lattices and an XY model on a Watts-Strogatz graph, which is a small-world network with random connectivity between spins.

2601.04172Jan 2026

View

The thermodynamics of liquid-vapor coexistence for a van der Waals fluid. Analytical solution of the Clausius-Clapeyron equation

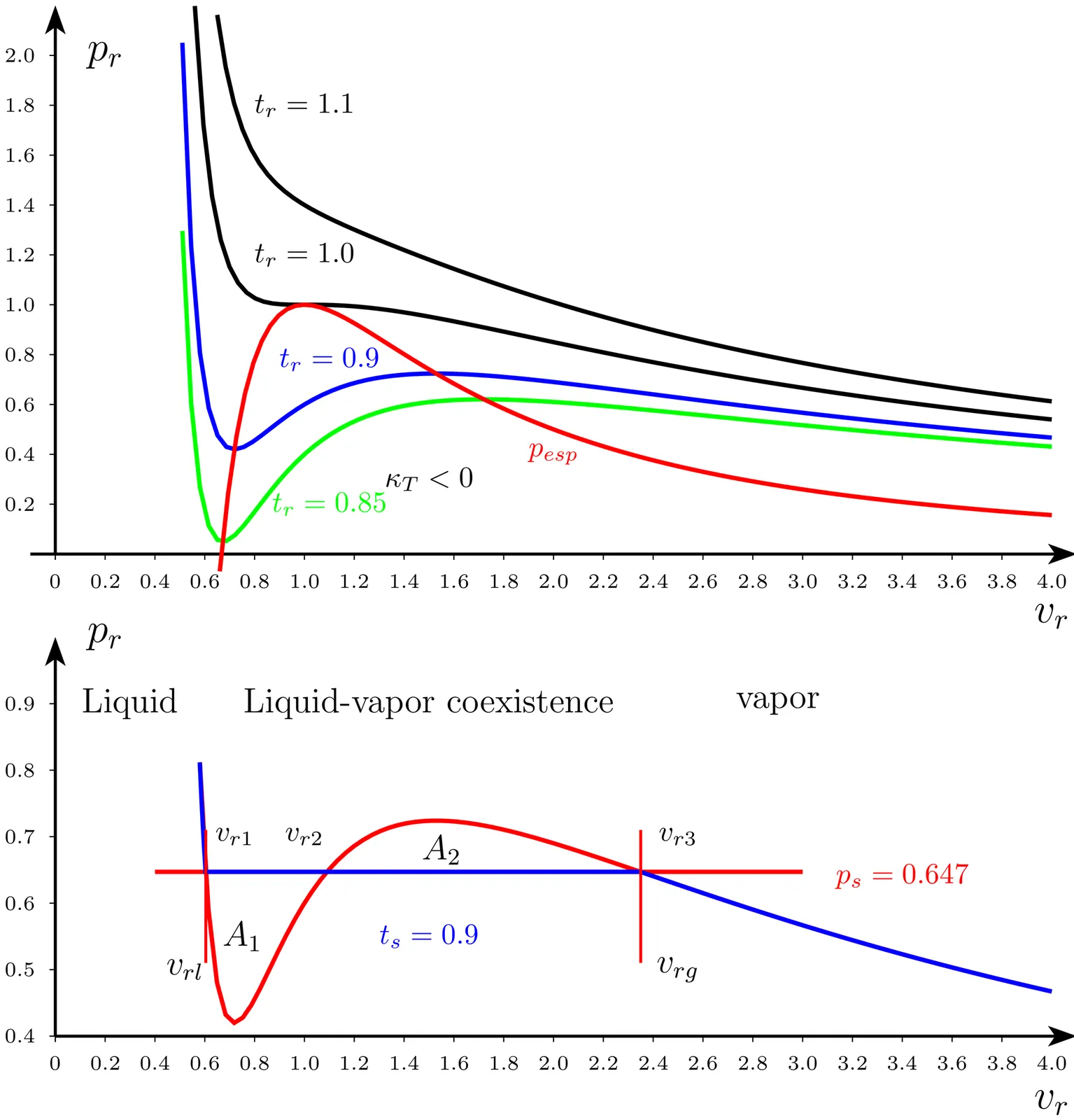
This work presents a pedagogical derivation of the thermodynamics of a van der Waals fluid by explicitly incorporating pairwise molecular interactions and the finite size of particles into the statistical-mechanical description. Starting from the Lennard-Jones potential, we evaluate the second virial coefficient to infer the virial expansion of the equation of state and recover the van der Waals equation using only its leading correction. The corresponding partition function allows us to obtain all thermodynamic potentials for both monoatomic and diatomic fluids in a transparent and instructive manner. Building on this framework, we formulate and solve analytically the Clausius-Clapeyron equation in the vicinity of the critical point, obtaining the liquid-vapor coexistence curve in closed form. This approach not only clarifies the microscopic origin of van der Waals thermodynamics but also complements-and in several aspects improves upon-traditional treatments that rely heavily on numerical methods or heuristic arguments. In addition, because the van der Waals equation naturally predicts the liquid-vapor equilibrium, the existence of critical points, and the functional form of the saturation curve of the pressure as a function of temperature, it provides an analytically tractable framework for studying a 150-year-old problem that has historically been addressed using graphical constructions or numerical solutions. As such, the formulation developed here offers a coherent, accessible, and conceptually unified route for students and instructors to understand phase coexistence in simple fluids from first principles.

2601.04296Jan 2026

View

Universality in driven systems with a multiply-degenerate umbilic point

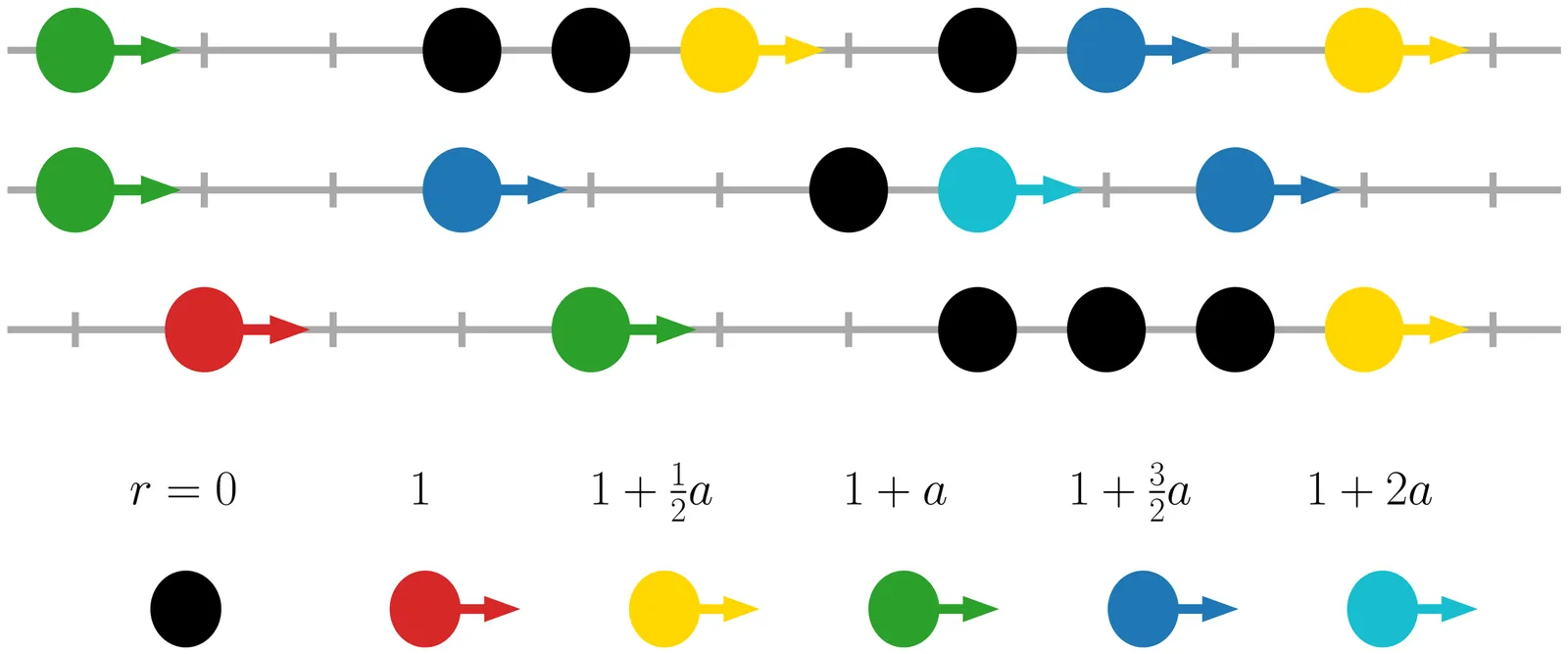
We investigate a driven particle system, a multilane asymmetric exclusion process, where the particle number in every lane is conserved, and stationary state is fully uncorrelated. The phase space has, starting from three lanes and more, an umbilic manifold where characteristic velocities of all the modes but one coincide, thus allowing us to study a weakly hyperbolic system with arbitrarily large degeneracy. We then study space-time fluctuations in the steady state, at the umbilic manifold, which are expected to exhibit universal scaling features. We formulate an effective mode-coupling theory (MCT) for the multilane model within the umbilic subspace and test its predictions. Unlike in the bidirectional two-lane model with an umbilic point studied earlier, here we find a robust $z=3/2$ dynamical exponent for the umbilic mode. The umbilic scaling function, obtained from Monte-Carlo simulations, for the simplest 3-lane scenario, appears to have an universal shape for a range of interaction parameters. Remarkably, the shape and dynamic exponent of the non-degenerate mode can be analytically predicted on the base of effective MCT, up to non-universal scaling factor. Our findings suggest the existence of novel universality classes with dynamical exponent $3/2$, appearing in long-lived hydrodynamic modes with equal characteristic velocities.

2601.04116Jan 2026

View

Random knotting in very long off-lattice self-avoiding polygons

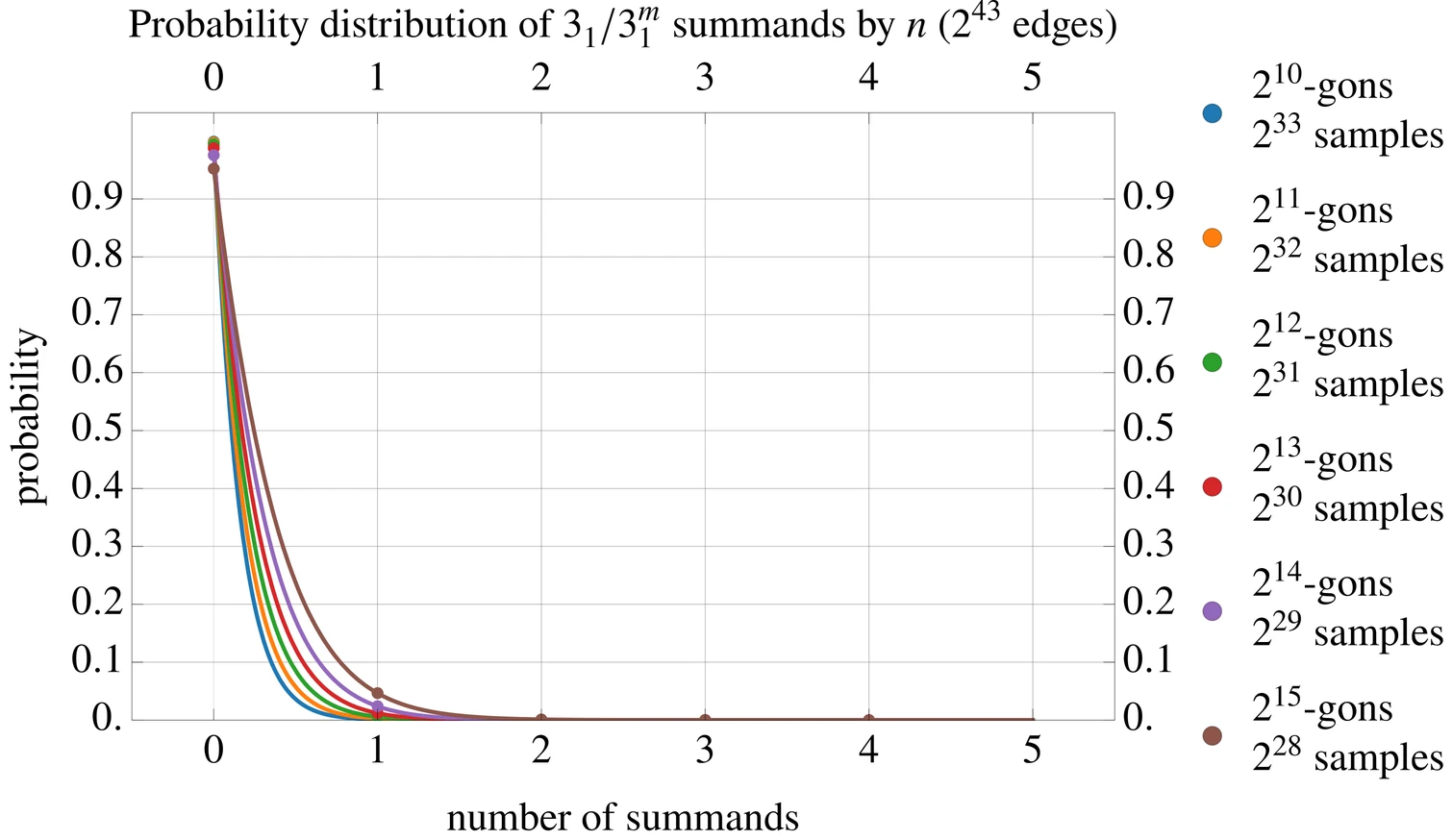
We present experimental results on knotting in off-lattice self-avoiding polygons in the bead-chain model. Using Clisby's tree data structure and the scale-free pivot algorithm, for each $k$ between $10$ and $27$ we generated $2^{43-k}$ polygons of size $n=2^k$. Using a new knot diagram simplification and invariant-free knot classification code, we were able to determine the precise knot type of each polygon. The results show that the number of prime summands of knot type $K$ in a random $n$-gon is very well described by a Poisson distribution. We estimate the characteristic length of knotting as $656500 \pm 2500$. We use the count of summands for large $n$ to measure knotting rates and amplitude ratios of knot probabilities more accurately than previous experiments. Our calculations agree quite well with previous on-lattice computations, and support both knot localization and the knot entropy conjecture.

2601.04102Jan 2026

View

Counterexamples to the conjectured ordering between the waiting-time bound and the thermodynamic uncertainty bound on entropy production

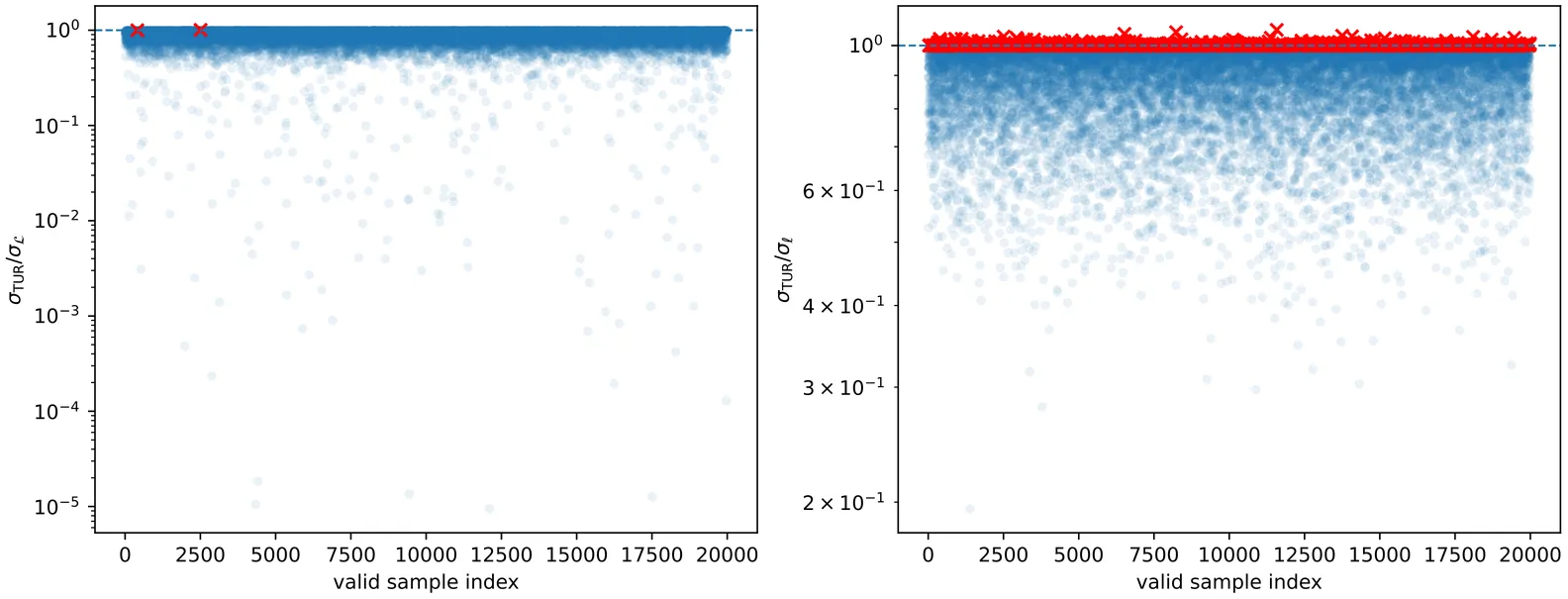
Two widely used model-free lower bounds on the steady-state entropy production rate of a continuous-time Markov jump process are the thermodynamic uncertainty relation (TUR) bound $σ_\text{TUR}$, derived from the mean and variance of a current, and the waiting-time distribution (WTD) bound $σ_\mathcal{L}$, derived from the irreversibility of partially observed transition sequences together with their waiting times. It has been conjectured that $σ_{\mathcal L}$ is always at least as tight as $σ_{\mathrm{TUR}}$ when both are constructed from the same partially observed link. Here we provide four-state counterexamples in a nonequilibrium steady state where $σ_{\mathcal L}<σ_{\mathrm{TUR}}$. This result shows that no universal ordering exists between these two inference bounds under partial observation.

2601.04039Jan 2026

View

Interplay of activity and non-reciprocity in tracer dynamics: From non-equilibrium fluctuation-dissipation to giant diffusion

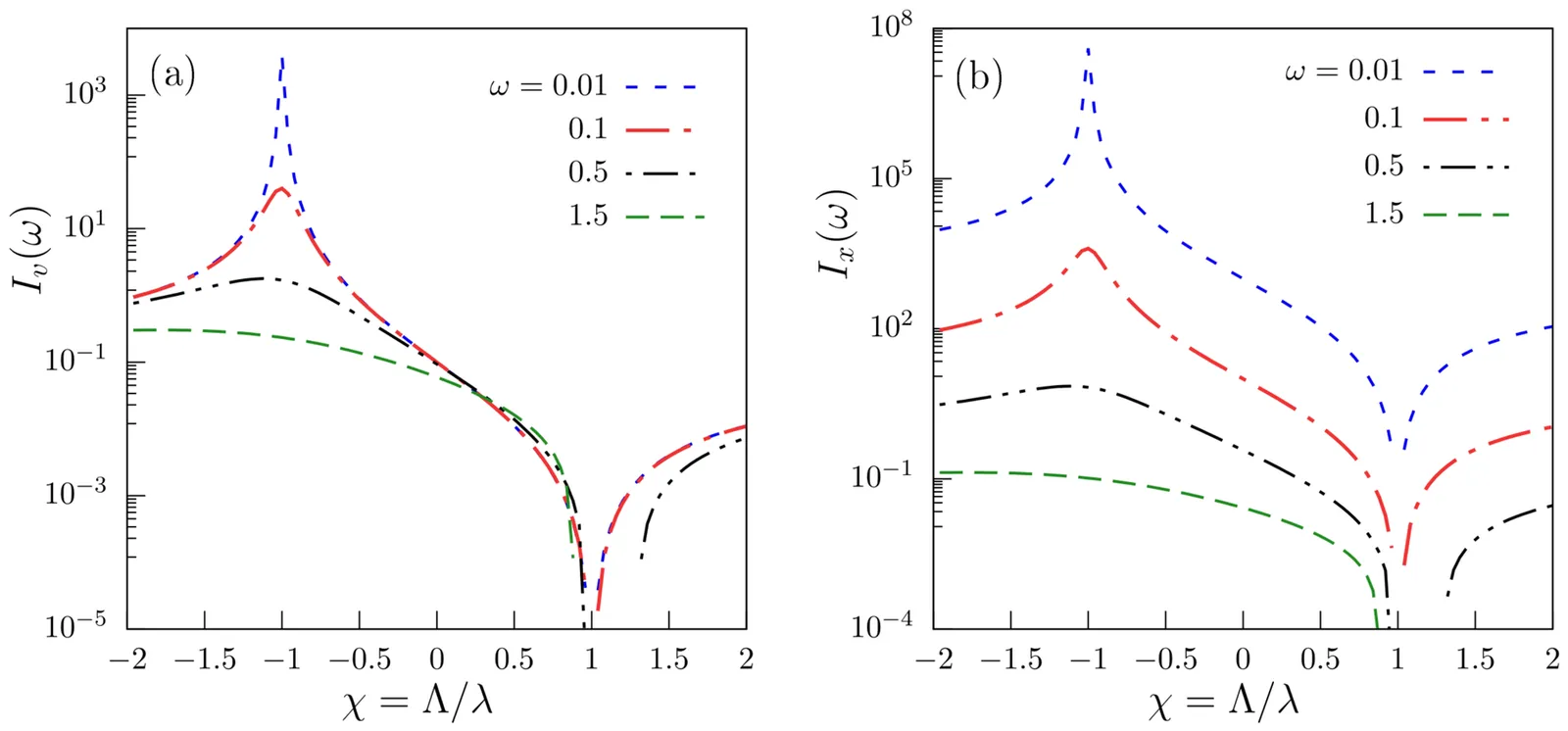
Non-reciprocal interactions play a key role in shaping transport in active and passive systems, giving rise to striking nonequilibrium behavior. Here, we study the dynamics of a tracer -- active or passive -- embedded in a bath of active or passive particles, coupled through non-reciprocal interactions. Starting from the microscopic stochastic dynamics of the full system, we derive an overdamped generalized Langevin equation for the tracer, incorporating a non-Markovian memory kernel that captures bath-mediated correlations. This framework enables us to compute the tracer's velocity and displacement response, derive a generalized nonequilibrium fluctuation-dissipation relation that quantifies deviations from equilibrium behavior, and determine the mean-squared displacement (MSD). We find that while the MSD becomes asymptotically diffusive, the effective diffusivity depends non-monotonically on the degree of non-reciprocity and diverges at an intermediate value. This regime of giant diffusivity provides a generic mechanism for enhanced transport in active soft matter and has direct implications for biological systems exhibiting chase-and-run or predator-prey interactions. Our analytical predictions are supported by numerical simulations of active Brownian particles, highlighting experimentally accessible signatures of non-reciprocal interactions in soft matter.

2601.03591Jan 2026

View

The Zubarev Double Time Greens function-A Vintage Many Body Technique

These lecture notes present a comprehensive and powerful many-body technique pioneered in 1960 by D. N. Zubarev. The technique, known as the Zubarev Double Time Greens Function method, was used extensively by leading solid state physicists such as John Hubbard and Laura Roth in the 1960s. We present the technique and apply it to the non-interacting electron and boson gas. We next consider the (many-body) Hubbard model and show how it yields the Stoner criterion for ferromagnetism. It is easily extendable to superconductivity and related problems. Our treatment is pedagogical and understandable to those with just an elementary understanding of second quantization.

2601.03439Jan 2026

View

Critical aging and relaxation dynamics in long-range systems

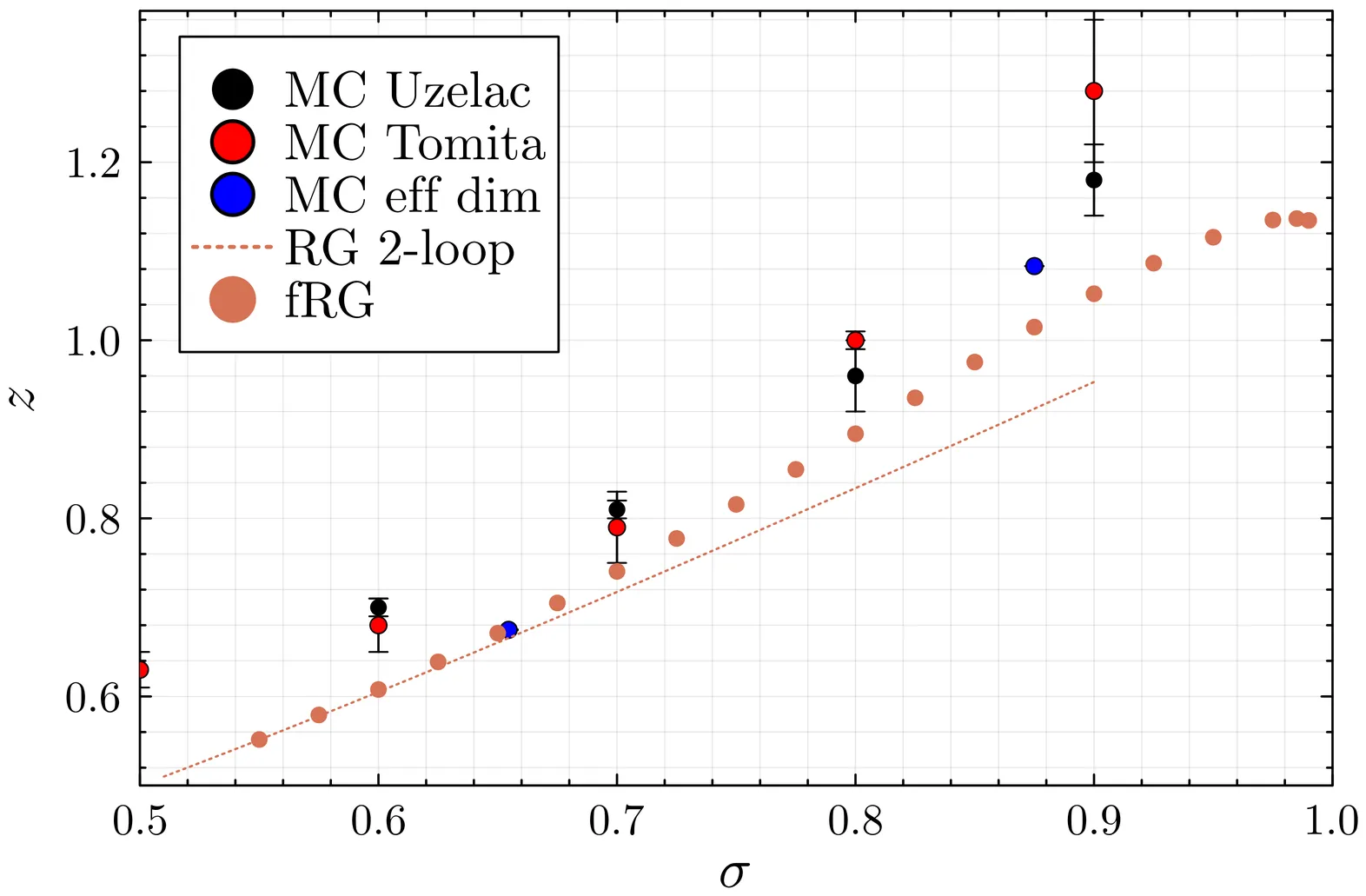
We study the dynamical scaling of long-range $\mathrm{O}(N)$ models after a sudden quench to the critical temperature, using the functional renormalization group approach. We characterize both short-time aging and long-time relaxation as a function of the symmetry index $N$, the interaction range decay exponent $σ$ and the dimension $d$. Our results substantially improve on perturbative predictions, as demonstrated by benchmarks against Monte Carlo simulations and the large-$N$ limit. Finally, we demonstrate that long-range systems increase the performance of critical heat engines with respect to a local active medium.

2601.03355Jan 2026

View

Consistent thermodynamics reconstructed from transitions between nonequilibrium steady-states

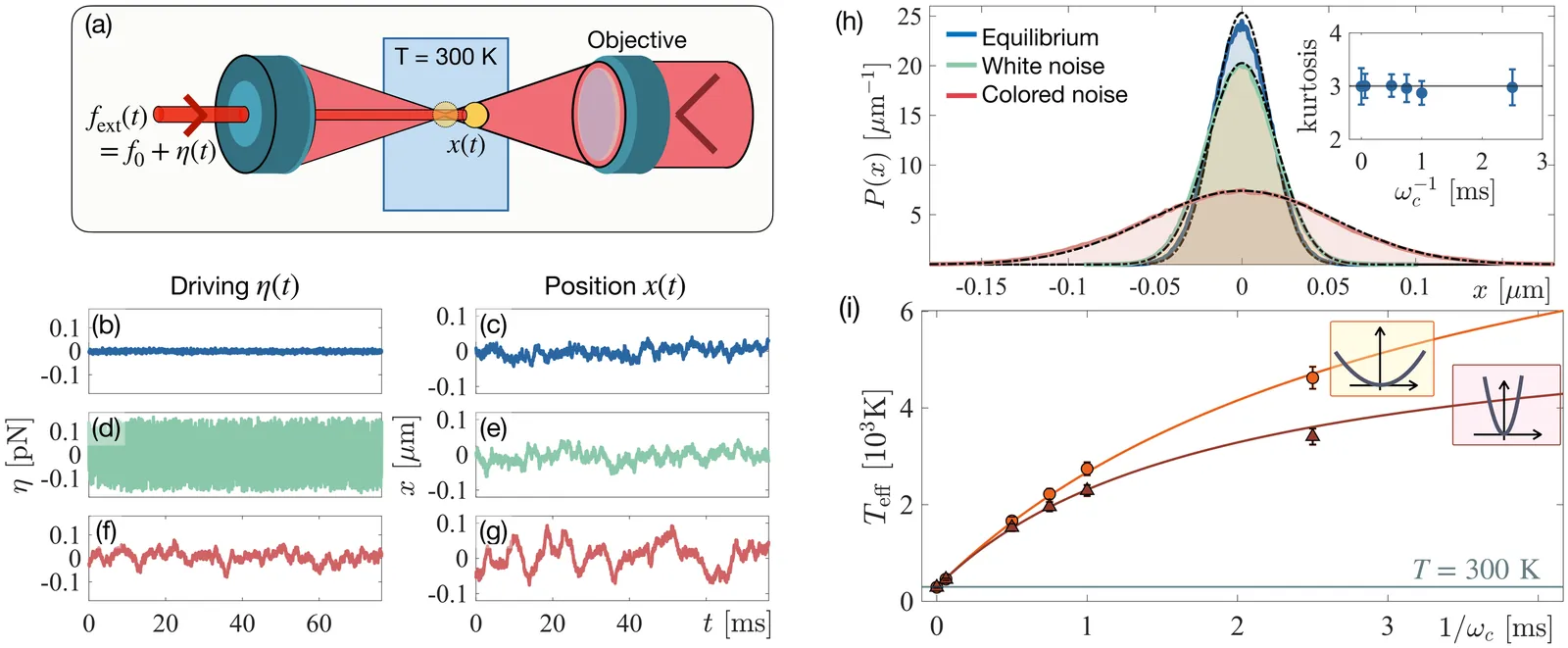
Constructing a thermodynamic framework for nonequilibrium systems remains a major challenge, as quantities such as temperature and free energy often become ambiguous when inferred solely from steady-state properties. Here we take a transformation-based approach and experimentally examine transitions between nonequilibrium steady states (NESS). Using an optically trapped microparticle driven by a tunable correlated stochastic force, we generate active-like steady states with controllable noise statistics. By abruptly changing the trap stiffness, we measure the stochastic work, heat, and entropy produced during NESS-to-NESS transformations. We identify a state-dependent effective temperature that restores the second law for these transitions, enabling the definition of a generalized work that incorporates the consequence of the nonequilibrium fluctuations. With this quantity, we derive and experimentally verify a Crooks-like fluctuation relation linking work distributions to a nonequilibrium free-energy difference defined through the effective temperature. Finally, we establish a fluctuation-response relation for the positional variance following stiffness changes. We demonstrate that this relation is key to distinguishing systems that can be described by a unique effective temperature (i.e., those under equilibrium or white-noise conditions) from those under colored-noise, where an equilibrium-like response cannot be restored. These results delineate the applicability and limits of effective-temperature thermodynamics in driven systems.

2601.03245Jan 2026

View

Propulsion dispersion mediated ordering transition in active particles

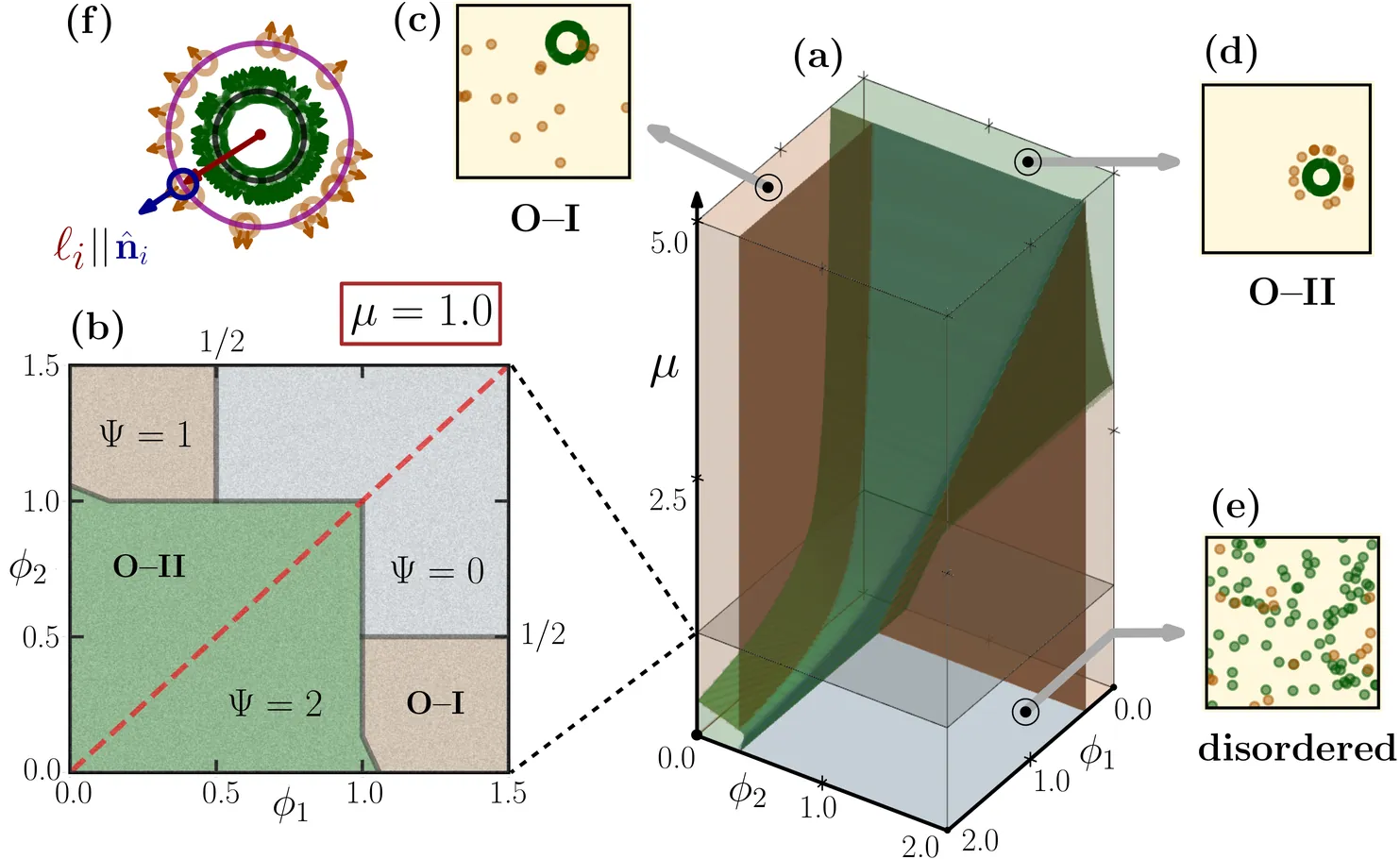
We show that dispersion in propulsion strength qualitatively alters collective behavior of active multi-particle systems interacting via short-range attractive potential, giving rise to novel ordered phases that combine spatial and orientational ordering. Considering a binary mixture of active Brownian particles with two distinct self-propulsion strengths, we find that, the interplay between interaction range, self-propulsion strengths and the relative numbers of the particles with different propulsion strengths can lead to three different phases, namely, a disordered one, and two ordered ones with partial and complete spatial and orientational ordering. The partially ordered phase is characterized by formation of a ring-like assembly of the slower particles while the faster particles diffuse randomly. Two concentric rings, comprising faster and slower particles, form in the fully ordered phase. Using the example of a truncated harmonic potential, we analytically characterize the phase boundaries and identify the associated order parameters. Our results demonstrate that propulsion dispersion provides a robust and novel route to collective ordering in attractive active matter.

2601.03174Jan 2026

View

Data-driven Reduction of Transfer Operators for Particle Clustering Dynamics

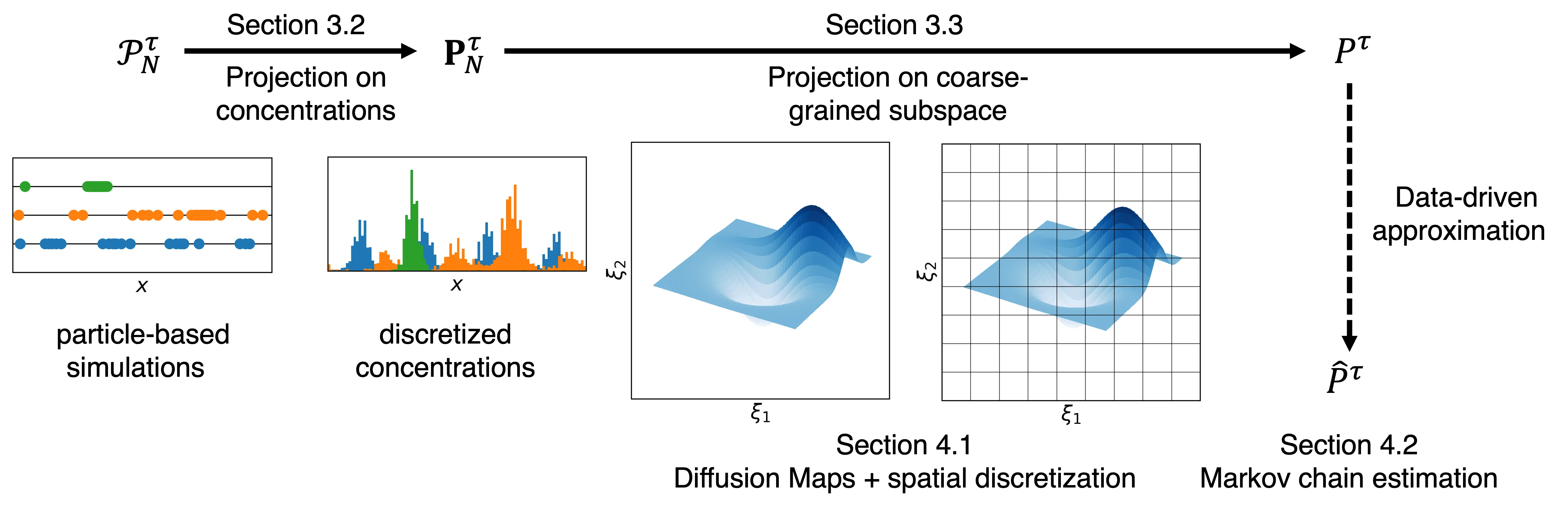
We develop an operator-based framework to coarse-grain interacting particle systems that exhibit clustering dynamics. Starting from the particle-based transfer operator, we first construct a sequence of reduced representations: the operator is projected onto concentrations and then further reduced by representing the concentration dynamics on a geometric low-dimensional manifold and an adapted finite-state discretization. The resulting coarse-grained transfer operator is finally estimated from dynamical simulation data by inferring the transition probabilities between the Markov states. Applied to systems with multichromatic and Morse interaction potentials, the reduced model reproduces key features of the clustering process, including transitions between cluster configurations and the emergence of metastable states. Spectral analysis and transition-path analysis of the estimated operator reveal implied time scales and dominant transition pathways, providing an interpretable and efficient description of particle-clustering dynamics.

2601.02932Jan 2026

View

Thermalized buckling of extensible, semiflexible polymers

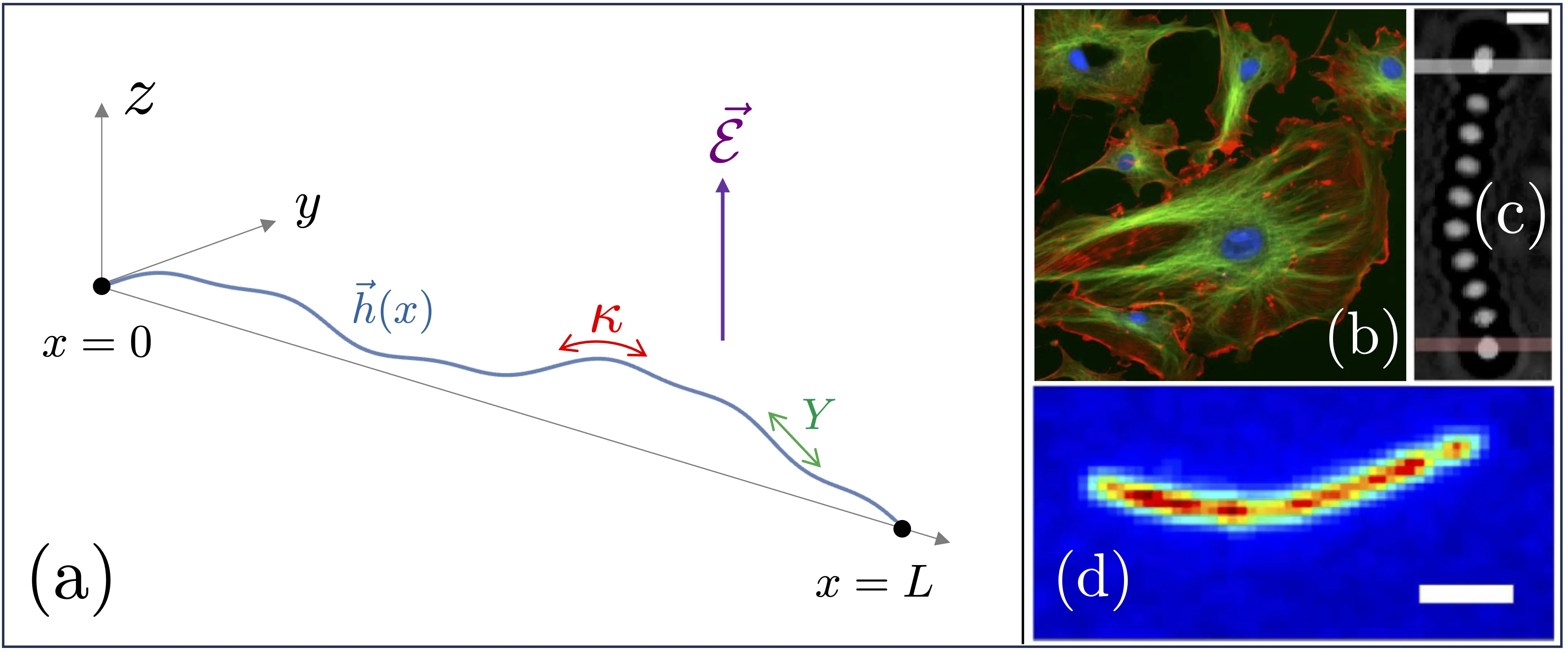
The Euler buckling of rods is a long-studied mechanical instability, and it remains relevant to this day, as the constituent components in many biological and physical systems are linear polymers, such as microtubules or carbon nanotubes. At finite temperature, if a polymer is shorter than its persistence length, the polymer is semiflexible, and its elasticity remains rod-like. But polymers can also stretch due to their finite extensibility, which can couple to energetically cheap bending deformations in nonlinear ways when a load is applied to the system. We show how the interplay between thermal fluctuations and nonlinear elasticity dramatically modifies the Euler buckling instability for compressed semiflexible polymers in a fixed strain ensemble. We identify a Ginzburg-like length scale beyond which thermally excited undulations lead to a softened Young's modulus, while the polymer nevertheless remains semiflexible. Both perturbative calculations and numerical Monte Carlo simulations suggest a qualitative change in several scaling properties of the buckling transition. The critical compressional strain for thermal buckling now increases with system size, in contrast to athermal buckling, where it decreases with system size. Renormalization group calculations confirm this picture, and also show that thermal buckling is controlled by a new fixed point with different critical exponents compared to classical Euler buckling.

2601.02654Jan 2026

View

Exact critical-temperature bounds for two-dimensional Ising models

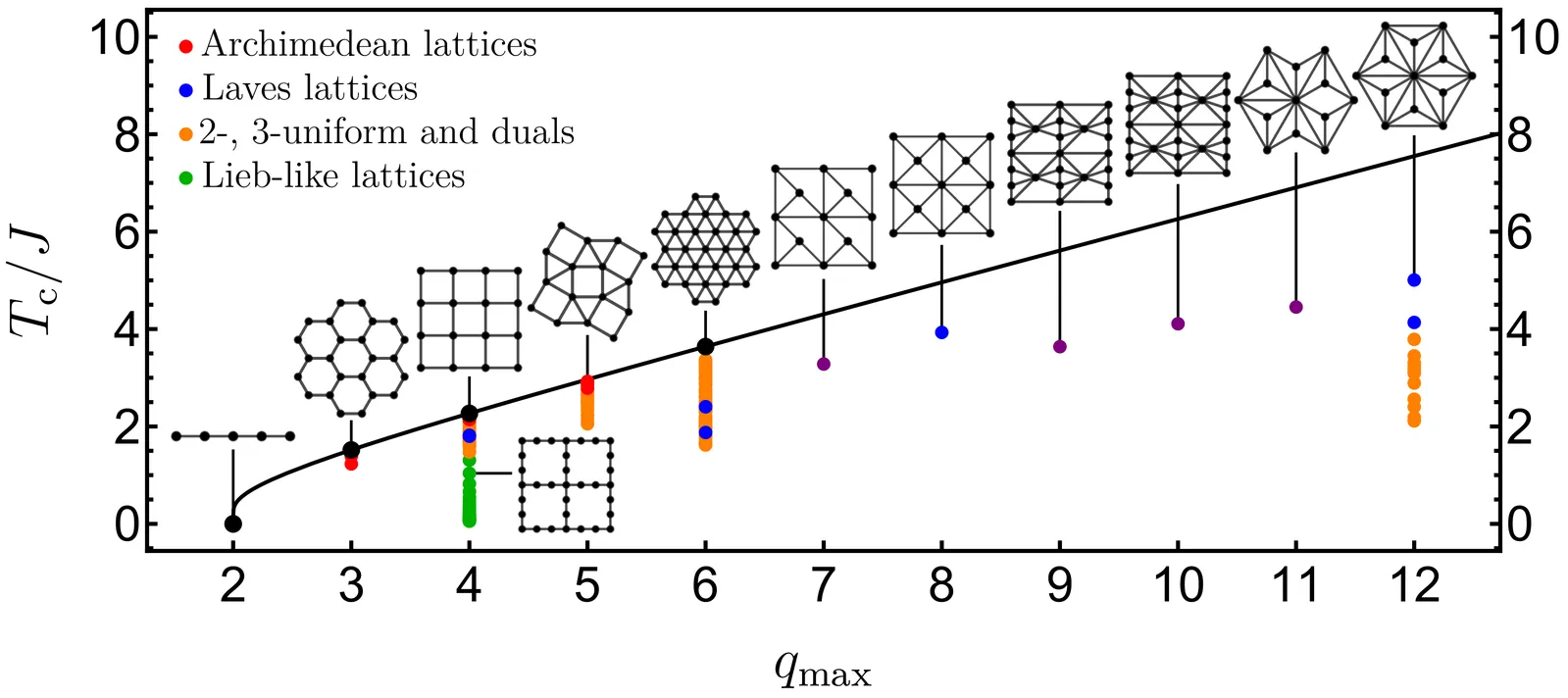
We derive exact critical-temperature bounds for the classical ferromagnetic Ising model on two-dimensional periodic tessellations of the plane. For any such tessellation or lattice, the critical temperature is bounded from a above by a universal number that is solely determined by the largest coordination number on the lattice. Crucially, these bounds are tight in some cases such as the Honeycomb, Square, and Triangular lattices. We prove the bounds using the Feynman--Kac--Ward formalism, confirm their validity for a selection of over two hundred lattices, and construct a two-dimensional lattice with 24-coordinated sites and record high critical temperature.

2601.02502Jan 2026

View

Page 1 of 31