Quantum Gases

arXiv:cond-mat.quant-gas

Ultracold atomic and molecular gases, Bose-Einstein condensation, Feshbach resonances, optical lattices.

Trending in Quantum Gases

Superfluid Fraction of a 2D Bose-Einstein Condensate in a Triangular Lattice

We experimentally investigate the superfluid properties of a two-dimensional, weakly interacting Bose-Einstein condensate in the zero-temperature regime, when it is subjected to a triangular optical lattice potential. We implement an original method, which involves solving the hydrodynamic continuity equation to extract the superfluid fraction tensor from the measured in situ density distribution of the fluid at rest. In parallel, we apply an independent dynamical approach that combines compressibility and sound velocity measurements to determine the superfluid fraction. Both methods yield consistent results in good agreement with simulations of the Gross-Pitaevskii equation as well as with the Leggett bounds determined from the measured density profiles.

2511.045752

Nov 2025Quantum Gases

Realization of repulsive polarons in the strongly correlated regime

Mobile impurities interacting with a quantum medium form quasiparticles known as polarons, a central concept in many-body physics. While the quantum impurity problem has been extensively studied with ultracold atomic gases, repulsive polarons in the strongly correlated regime have remained elusive. Typically, the impurity atoms bind into molecules or rapidly decay into deeper lying states before they can acquire an appreciable dressing cloud. Here, we report on the realization of polarons in a strongly repulsive quasi-two-dimensional quantum gas. Using a superfluid of $^6$Li dimers, we introduce impurities by promoting a small fraction of the dimers into higher levels of the transverse confining potential. These novel synthetic-spin polarons give access to the strongly repulsive regime where common decay channels are suppressed. We extract key polaron properties - the energy, quasiparticle residue, and effective mass - using trap modulation and Bragg spectroscopy. Our measurements are well captured by a microscopic T-matrix approach and quantum Monte Carlo simulations, revealing deviations from mean-field predictions. In particular, we measure a significant enhancement of the polaron mass, with values exceeding twice the free dimer mass. Our demonstration of a stable repulsive Bose polaron establishes a platform for studying impurity physics in low-dimensional and strongly correlated systems.

2511.035691

Nov 2025Quantum Gases

Majorana string simulation of nonequilibrium dynamics in two-dimensional lattice fermion systems

The study of real-time dynamics of fermions remains one of the last frontiers beyond the reach of classical simulations and is key to our understanding of quantum behavior in chemistry and materials, with implications for quantum technology. Here we introduce a Heisenberg-picture algorithm that propagates observables expressed in a Majorana-string basis using a truncation scheme that preserves Trotter accuracy and aims at maintaining computational efficiency. The framework is exact for quadratic Hamiltonians--remaining restricted to a fixed low-weight sector determined by the physical observable--admits variational initial states, and can be extended to interacting regimes via systematically controlled truncations. We benchmark our approach on one- and two-dimensional Fermi-Hubbard quenches, comparing against tensor network methods (MPS and fPEPS) and recent experimental data. The method achieves high accuracy on timescales comparable to state-of-the-art variational techniques and experiments, demonstrating that controlled Majorana-string truncation is a practical tool for simulating two-dimensional fermionic dynamics.

2511.028091

Nov 2025Quantum Gases

Multi-Particle Quantum Walks in a Dipole-Conserving Bose-Hubbard Model

When particles move through a crystal or optical lattice, their motion can sometimes become frozen by strong external forces -- yet collective motion may still emerge through subtle many-body effects. In this work, we explore such constrained dynamics by realizing a dipole-conserving Bose-Hubbard model, where single atoms are immobile but pairs of particles can move cooperatively while preserving the system's center of mass, i.e. the overall dipole moment of the particle distribution. Starting from a one-dimensional chain of ultracold bosonic atoms in an optical lattice, we generate localized dipole excitations consisting of a hole and a doublon using site-resolved optical potentials and characterize their quantum walks and scattering dynamics. Our study provides a bottom-up investigation of a Hamiltonian with kinetic constraints, and paves the way for exploring low-energy phases of fractonic matter in existing experimental platforms.

2511.023431

Nov 2025Quantum Gases

Connected correlations in cold atom experiments

The recent development of single-atom-resolved probes has made full counting statistics measurements accessible in quantum gas experiments. This capability provides access to high-order moments of physical observables, from which cumulants, or equivalently connected correlations, can be precisely determined. Through a selection of recent cold atom experiments, this article illustrates the significance of connected correlations in characterizing ensembles of interacting quantum particles. First, non-zero connected correlations of order n > 2 unambiguously identify non-Gaussian quantum states. Second, connected correlations of order n identify clusters made of n elements whose statistical properties are irreducible to combinations of smaller clusters. The ability to identify such multi-particle clusters offers a an interesting perspective on strongly correlated quantum states of matter at the microscopic scale.

2511.004481

Nov 2025Quantum Gases

Single-fluid model for rotating annular supersolids and its experimental implications

The famous two-fluid model of finite-temperature superfluids has been recently extended to describe the mixed classical-superfluid dynamics of the newly discovered supersolid phase of matter. We show that for rigidly rotating supersolids one can derive a more appropriate single-fluid model, in which the seemingly classical and superfluid contributions to the motion emerge from a spatially varying phase of the global wavefunction. That allows to design experimental protocols to excite and detect the peculiar rotation dynamics of annular supersolids, including partially quantized supercurrents, in which each atom brings less than $\hbar$ unit of angular momentum. Our results are valid for a more general class of density-modulated superfluids.

2510.267531

Oct 2025Quantum Gases

Universal Random Matrix Behavior of a Fermionic Quantum Gas

The pursuit of universal governing principles is a foundational endeavor in physics, driving breakthroughs from thermodynamics to general relativity and quantum mechanics. In 1951, Wigner introduced the concept of a statistical description of energy levels of heavy atoms, which led to the rise of Random Matrix Theory (RMT) in physics. The theory successfully captured spectral properties across a wide range of atomic systems, circumventing the complexities of quantum many-body interactions. Rooted in the fundamental principles of stochasticity and symmetry, RMT has since found applications and revealed universal laws in diverse physical contexts, from quantum field theory to disordered systems and wireless communications. A particularly compelling application arises in describing the mathematical structure of the many-body wavefunction of non-interacting Fermi gases, which underpins a complex spatial organization driven by Pauli's exclusion principle. However, experimental validation of the counting statistics predicted in such systems has remained elusive. Here, we probe at the single-atom level ultracold atomic Fermi gases made of two interacting spin states, obtaining direct access to their counting statistics in situ. Our measurements show that, while the system is strongly attractive, each spin-component is extremely well described by RMT predictions based on Fredholm determinants. Our results constitutes the first experimental validation of the Fermi-sphere point process through the lens of RMT, and establishes its relevance for strongly-interacting systems.

2510.257352

Oct 2025Quantum Gases

Entanglement-enhanced correlation propagation in the one-dimensional SU($N$) Fermi-Hubbard model

We investigate the dynamics of correlation propagation in the one-dimensional Fermi-Hubbard model with SU($N$) symmetry when the replusive-interaction strength is quenched from a large value, at which the ground state is a Mott-insulator with $1/N$ filling, to an intermediate value. From approximate analytical insights based on a simple model that captures the essential physics of the doublon excitations, we show that entanglement in the initial state leads to collective enhancement of the propagation velocity $v_{\text{SU}(N)}$ when $N>2$, becoming equal to the velocity of the Bose-Hubbard model in the large-$N$ limit. These results are supported by numerical calculations of the density-density correlation in the quench dynamics for $N=2,3,4,$ and $6$.

2510.253581

Oct 2025Quantum Gases

Observation of vector rogue waves in repulsive three-component atomic mixtures

We report the experimental observation of vector extensions of Peregrine solitons in highly particle-imbalanced, pairwise immiscible three-component repulsive Bose-Einstein condensates (BECs). The possibility of an effectively attractive character of the minority components is established by constructing a generalized reduction scheme for an imbalanced N-component setup with arbitrary interaction signs. These components may suffer intra- and inter-component modulation instability, which along with the presence of an attractive potential well induces the dynamical formation of highly reproducible vector rogue waves. Exploiting different Rb hyperfine states, it is possible to flexibly tune the effective interactions stimulating the realization of a plethora of vector rogue waves, including single and double Peregrine-like wave peaks. The experimental findings are in quantitative agreement with suitable three-dimensional mean-field simulations, while quasi-one-dimensional analysis of the non-polynomial Schrödinger model provides additional insights into the rogue wave characteristics.

2510.249171

Oct 2025Quantum Gases

Coupling-induced universal dynamics in bilayer two-dimensional Bose gases

The emergence of order in many-body systems and the associated self-similar dynamics governed by dynamical scaling laws is a hallmark of universality far from equilibrium. Measuring and classifying such nontrivial behavior for novel symmetry classes remains challenging. Here, we realize a well-controlled interlayer coupling quench in a tunable bilayer two-dimensional Bose gas, driving the system to an ordered phase. We observe robust self-similar dynamics and a universal critical exponent consistent with diffusion-like coarsening, driven by vortex and antivortex annihilation induced by the interlayer coupling. Our results extend the understanding of universal dynamics in many-body systems and provide a robust foundation for quantitative tests of nonequilibrium effective field theories.

2510.236001

Oct 2025Quantum Gases

Trapping, manipulating and probing ultracold atoms: a quantum technologies tutorial

Engineered ultracold atomic systems are a valuable platform for fundamental quantum mechanics studies and the development of quantum technologies. At near zero absolute temperature, atoms exhibit macroscopic phase coherence and collective quantum behavior, enabling their use in precision metrology, quantum simulation, and even information processing. This review provides an introductory overview of the key techniques used to trap, manipulate, and detect ultracold atoms, while highlighting the main applications of each method. We outline the principles of laser cooling, magnetic and optical trapping, and the most widely used techniques, including optical lattices and tweezers. Next, we discuss the manipulation methods of atomic internal and external degrees of freedom, and we present atom interferometry techniques and how to leverage and control interatomic interactions. Next, we review common ensemble detection strategies, including absorption and fluorescence imaging, state-selective readout, correlation and quantum non-demolition measurements and conclude with high-resolution approaches. This review aims to provide newcomers to the field with a broad understanding of the experimental toolkit that underpins research in ultracold atom physics and its applications across quantum science and technology.

2510.207904

Oct 2025Quantum Gases

Breaking of scale invariance in a strongly dipolar 2D Bose gas

Two-dimensional (2D) dipolar atomic gases present unique opportunities for exploring novel quantum phases due to their anisotropic and long-range interactions. However, the behavior of strongly dipolar Bose gases in 2D remains unclear, especially when dipoles are tilted. Here, we demonstrate the creation and characterization of strongly dipolar 2D condensates in a quasi-2D harmonic trap with tunable dipole orientation. By investigating scale invariance properties through breathing collective mode measurements, we observe significant breaking of scale invariance when dipoles are tilted in-plane indicating the dominance of the nonlocal dipole-dipole interactions (DDIs) in this regime. Interestingly, the breaking of the scale invariant dynamics is accompanied by an increase in quantum fluctuations, as shown by comparison with mean-field and beyond mean-field theoretical studies. Our experiments also reveal that at critical tilt angles around 70°, stripe-type density modulations emerge, suggesting the presence of a roton spectrum in 2D, while the system still shows hydrodynamic nature with the phase-locking breathing behavior. This observation elucidates the many-body effect induced by DDIs in 2D, thus marking a crucial step toward realizing 2D supersolids and other exotic quantum phases.

2510.137302

Oct 2025Quantum Gases

From elastic to inelastic deformation of a dipolar supersolid

Due to its peculiar superfluid-crystal duality feature, supersolid has received great research interest. Recently, researchers have paid much attention to its elastic response properties; however, the inelastic deformation has barely been explored. In this work, we study the transition from elastic to inelastic deformation of a dipolar supersolid Bose-Einstein condensate trapped in a box potential (i.e., a dipolar supersolid with finite size). We obtained the stationary supersolid states (both ground and excited) of the system, and examined the relation between the supersolid size and the number of unit cells it can accommodate, which can essentially help us to understand the dynamical responses of the supersolid during a dilation or compression process. We found that within a certain dilation or compression extent, the supersolid can retain its original crystal structure, that is, it endures an elastic deformation; however, when the extent exceeds a critical threshold, the original crystal structure of the supersolid will be disrupted, which signifies an inelastic deformation. Furthermore, we both analytically and numerically determined the critical point of the transition from elastic to inelastic deformation, and mapped out a phase diagram. These results open up new territory in the research of supersolid mechanical properties, and may find applications in quantum material science and quantum-based technologies.

2510.130861

Oct 2025Quantum Gases

The Infra-Red Road to Quantum Gravity

We review work in areas ranging from condensed matter physics to quantum gravity, with the following interconnected questions in mind: (i) what is the nature of the vacuum in condensed matter systems, in quantum field theory, and in classical and quantum gravity; (ii) how do analogies between these systems work, how well do they work, and how useful are they; (iii) what modifications can we make to quantum mechanics to deal with quantum gravity, and (iv) how and why low-energy theories of quantum gravity are, in our view, the right way to make progress in this field. We use many different examples to illustrate our arguments.

2510.129771

Oct 2025Quantum Gases

Stable High-Order Vortices in Spin-Orbit-Coupled Spin-1 Bose-Einstein Condensates

The present contribution explores phase transitions that occur in the ground state (GS) of spin-1 Bose-Einstein condensates (BECs) with spin-orbit coupling (SOC) under the action of gradient magnetic fields. By solving the corresponding linearized system in an exact fashion, we identify the conditions under which the GS phase transitions occur, thus transforming excited states into GS. The study of the full nonlinear system, including both density-density and spin-spin interactions, is numerically analyzed. For the case of repulsive spin-spin interactions, the results resemble the linear case, while attractive spin-spin interactions lead to the formation of mixed-states near the GS phase-transition points. Additionally, higher-order vortex solitons are found to be stable even in the nonlinear regime. These findings demonstrate that arbitrary winding numbers can be achieved as corresponding to stable GS and thus contributing to the understanding of topological properties in SOC BECs.

2510.098321

Oct 2025Quantum Gases

Vacuum tunneling of vortices in two-dimensional $^4$He superfluid films

At low temperature T we expect vacuum tunneling processes to occur in superfluid $^{4}$ He films. We distinguish between extrinsic processes, in which single vortices nucleate by tunneling off boundaries in the system, and intrinsic processes, in which vortex/anti-vortex pairs nucleate far from boundaries. It is crucial to incorporate the varying effective mass of the vortex in tunneling calculations. The intrinsic processes are the superfluid analogue of the Schwinger mechanism in quantum field theory; here they appear as a quantum phase transition at T = 0, driven by an external supercurrent. We calculate the tunneling rate for these processes, and describe a means of testing the predictions using a specific vortex counting experiment.

2510.128241

Oct 2025Quantum Gases

Faraday patterns, spin textures, spin-spin correlations and competing instabilities in a driven spin-1 antiferromagnetic Bose-Einstein condensate

We study the formation of transient Faraday patterns and spin textures in driven quasi-one-dimensional and quasi-two-dimensional spin-1 Bose-Einstein condensates under the periodic modulation of $s$-wave scattering lengths $a_0$ and $a_2$, starting from the anti-ferromagnetic phase. This phase is characterized by a Bogoliubov spectrum consisting of three modes: one mode is gapped, while the other two are gapless. When $a_0$ is modulated and half of the modulation frequency lies below the gapped mode, density and spin Faraday patterns emerge. In that case, in quasi-one-dimension, the spin texture is characterized by periodic domains of opposite $z$-polarizations. When driven above the gap, the spin texture is characterized by random orientations of spin vectors along the condensate axis. Qualitatively new features appear in the driven quasi-two-dimensional condensate. For instance, when driven above the gap, the spin textures are characterized by anomalous vortices and antivortices that do not exhibit phase winding in individual magnetic components. Below the gap, the spin texture exhibits irregular ferromagnetic patches with opposite polarizations. The spatial spin-spin correlations in quasi-one-dimension exhibit a Gaussian envelope, whereas they possess a Bessel function dependence in quasi-two-dimension. Under the $a_2$-modulation, the density patterns dominate irrespective of the driving frequency, unless the spin-dependent interaction strength is sufficiently smaller than that of the spin-independent interaction. The intriguing scenario of competing instability can emerge when both scattering lengths are simultaneously modulated. Finally, we show that the competing instabilities result in a complex relationship between the population transfer and the strength of the quadratic Zeeman field, while keeping all other parameters constant.

2510.080871

Oct 2025Quantum Gases

Encoding a topological gauge theory on a ring-shaped Raman-coupled Bose gas

Topological gauge theories constitute a framework for understanding strongly correlated quantum matter in terms of weakly interacting composite degrees of freedom. Their topological properties become evident when these theories are realized on a space of non-trivial topology. Here, we propose a scheme to realize a one-dimensional topological gauge theory, the chiral BF theory, on a ring geometry. We obtain such a theory by dimensionally reducing Chern-Simons theory on a disk to the so-called chiral BF theory defined on the ring. Then, we encode the theory into a Hamiltonian with a coupling between angular momentum and density, and we propose and numerically benchmark its realization in an optically-dressed Bose gas confined in a ring-shaped trap. There, the topological properties of the underlying theory manifest themselves through a magnetic flux variable that is density-dependent. We quantify such density-dependent magnetic flux in terms of the ground-state angular momentum and the chiral properties of the system through a Bogoliubov analysis. Our proposal enables the observation of the interplay between the topology of the theory and that of the space.

2510.060891

Oct 2025Quantum Gases

Rogue waves in extended Gross-Pitaevskii Models with a Lee-Huang-Yang correction

We explore the existence and dynamical generation of rogue waves (RWs) within a one dimensional quantum droplet bearing environment. RWs are computed by deploying a spacetime fixed point scheme to the relevant extended Gross Pitaevskii equation (eGPE). Parametric regions where the ensuing RWs are different from their counterparts in the nonlinear Schroedinger equation are identified. To corroborate the controllable generation, relevant to ultracold atom experiments, of these rogue patterns we exploit two different protocols. The first is based on interfering dam break flows emanating from Riemann initial conditions and the second refers to the gradient catastrophe of a spatially localized waveform. A multitude of possible RWs are found in this system, spanning waveforms reminiscent of the Peregrine soliton, its spatially periodic variants, namely, the Akhmediev breathers, and other higher order RW solutions of the nonlinear Schroedinger equation. Key elements of the shape of the corresponding eGPE RWs traced back to nonintegrability and the presence of competing interactions are discussed. Our results set the stage for probing a multitude of unexplored rogue like waveforms in such mixtures with competing interactions and should be accessible to current ultracold atom experiments.

2510.030631

Oct 2025Quantum Gases

Observation of non-Hermitian topology in cold Rydberg quantum gases

The pursuit of topological phenomena in non-Hermitian systems has unveiled new physics beyond the conventional Hermitian paradigm, yet their realization in interacting many-body platforms remains a critical challenge. Exploring this interplay is essential to understand how strong interactions and dissipation collectively shape topological phases in open quantum systems. Here, we experimentally demonstrate non-Hermitian spectra topology in a dissipative Rydberg atomic gas and characterize parameters-dependent winding numbers. By increasing the interaction strength, the system evolves from Hermitian to non-Hermitian regime, accompanying emergence of trajectory loop in the complex energy plane. As the scanning time is varied, the spectra topology becomes twisted in the complex energy plane manifesting as a topology phase transition with the sign winding number changed. When preparing the system in different initial states, we can access a nontrivial fractional phase within a parameter space that globally possesses an integer winding. Furthermore, by changing the scanning direction, we observe the differentiated loops, revealing the breaking of chirality symmetry. This work establishes cold Rydberg gases as a versatile platform for exploring the rich interplay between non-Hermitian topology, strong interactions, and dissipative quantum dynamics.

2509.262561

Sep 2025Quantum Gases

Related categories:

Disordered Systems and Neural Networks Mesoscale and Nanoscale Physics Materials Science Other Condensed Matter Soft Condensed Matter

243 papers

Topological sensing of superfluid rotation using non-Hermitian optical dimers

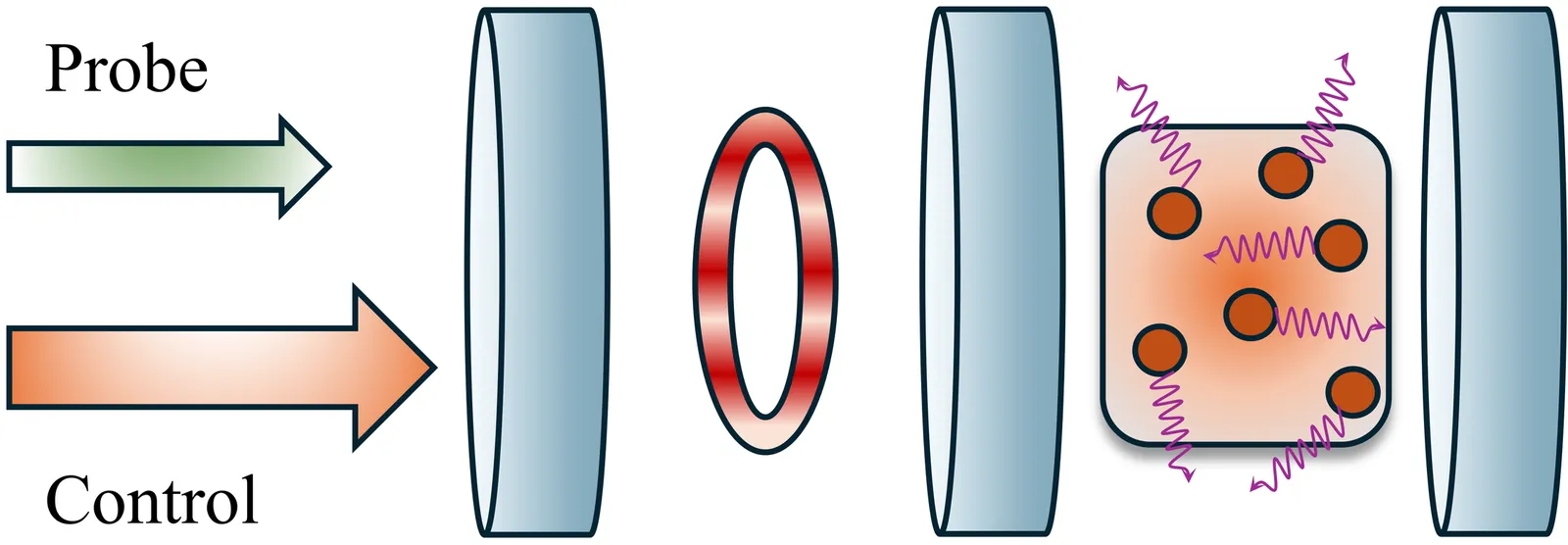
We theoretically investigate a non-Hermitian optical dimer whose parameters are renormalized by dispersive and dissipative backaction from the coupling of the passive cavity with a ring-trapped Bose-Einstein condensate. The passive cavity is driven by a two-tone control laser, where each tone is in a coherent superposition of Laguerre-Gaussian beams carrying orbital angular momenta $\pm \ell \hbar$. This imprints an optical lattice on the ring trap, leading to Bragg-diffracted sidemode excitations. Using an exact Schur-complement reduction of the full light-matter dynamics, we derive a frequency-dependent self-energy and identify a static regime in which the atomic response produces a complex shift of the passive optical mode. This renormalized dimer supports a tunable exceptional point, enabling spectroscopic signatures in the optical transmission due to a probe field, which can in turn be utilized for estimating the winding number of the persistent current. Exploiting the associated half-integer topological charge, we propose a digital exceptional-point-based sensing scheme based on eigenmode permutation, providing a noise-resilient method to sense superfluid rotation without relying on fragile eigenvalue splittings. Importantly, the sensing proposals are intrinsically non-destructive, preserving the coherence of the atomic superfluid.

2601.04749Jan 2026

View

Scalable cold-atom quantum simulator of a $3+1$D U$(1)$ lattice gauge theory with dynamical matter

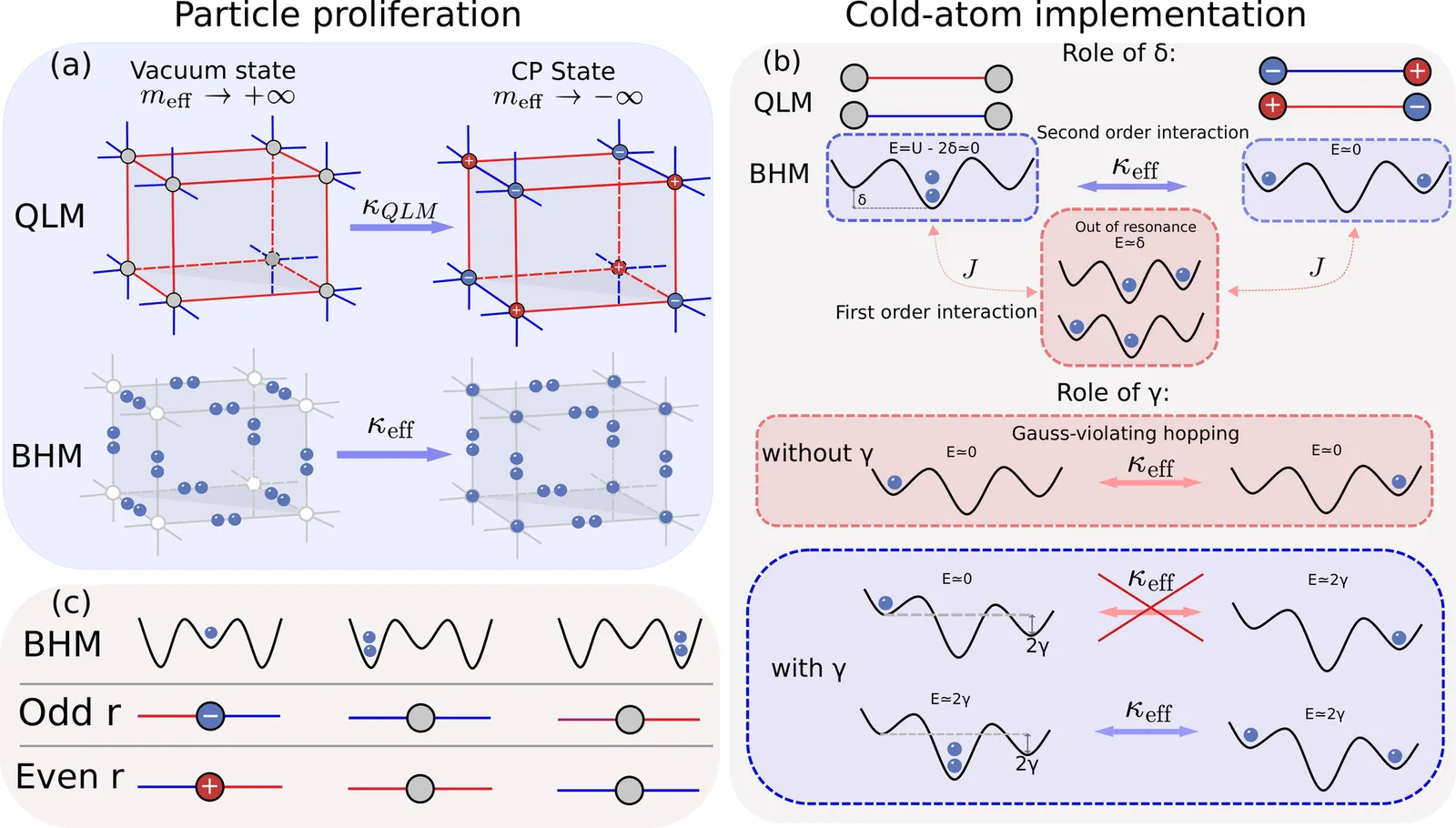
The stated overarching goal of the highly active field of quantum simulation of high-energy physics (HEP) is to achieve the capability to study \textit{ab-initio} real-time microscopic dynamics of $3+1$D quantum chromodynamics (QCD). However, existing experimental realizations and theoretical proposals for future ones have remained restricted to one or two spatial dimensions. Here, we take a big step towards this goal by proposing a concrete experimentally feasible scalable cold-atom quantum simulator of a U$(1)$ quantum link model of quantum electrodynamics (QED) in three spatial dimensions, employing \textit{linear gauge protection} to stabilize gauge invariance. Using tree tensor network simulations, we benchmark the performance of this quantum simulator through near- and far-from-equilibrium observables, showing excellent agreement with the ideal gauge theory. Additionally, we introduce a method for \textit{analog quantum error mitigation} that accounts for unwanted first-order tunneling processes, vastly improving agreement between quantum-simulator and ideal-gauge-theory results. Our findings pave the way towards realistic quantum simulators of $3+1$D lattice gauge theories that can probe regimes well beyond classical simulability.

2601.04345Jan 2026

View

Interference-Induced Suppression of Doublon Transport and Prethermalization in the Extended Bose-Hubbard Model

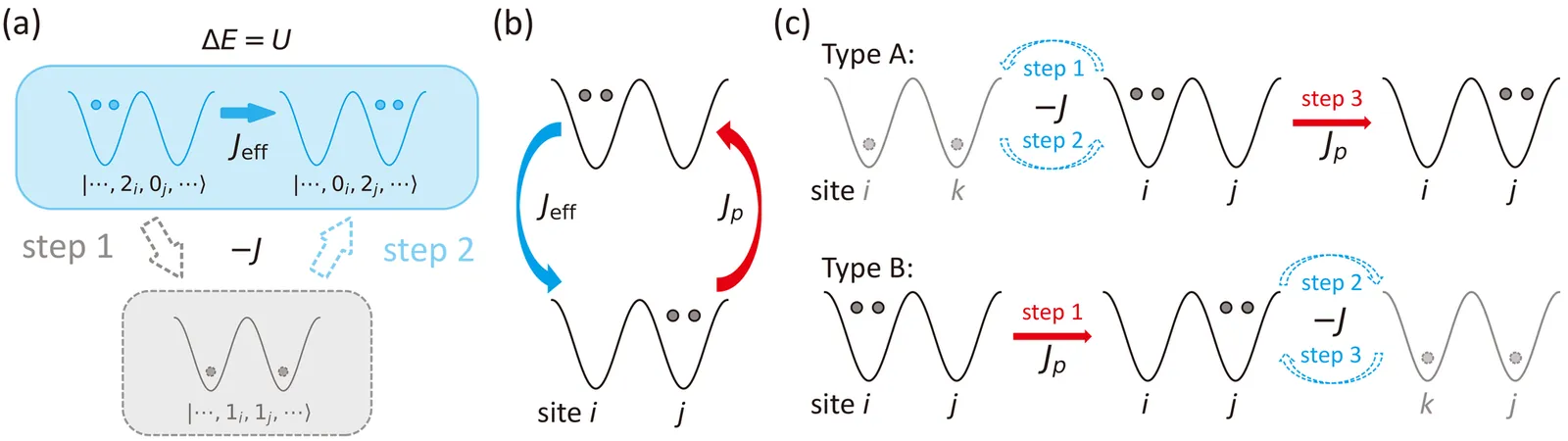
The coherent mobility of doublons, arising from second-order virtual dissociation-recombination processes, fundamentally limits their use as information carriers in the strongly interacting Bose-Hubbard model. We propose a disorder-free suppression mechanism by introducing an optimized nearest-neighbor pair-hopping term that destructively interferes with the dominant virtual hopping channel. Using the third-order Schrieffer-Wolff transformation, we derive an analytical optimal condition that accounts for lattice geometry corrections. Exact numerical simulations demonstrate that this optimized scheme achieves near-complete dynamical arrest and entanglement preservation in one-dimensional chains, while in two-dimensional square lattices, it significantly suppresses ballistic spreading yet permits a slow residual expansion. Furthermore, in the many-body regime, finite-size scaling analysis identifies the observed long-lived density-wave order as a prethermal plateau emerging from the dramatic separation of microscopic and thermalization timescales.

2601.03694Jan 2026

View

Ground State and Collective Modes of Bose-Einstein Condensates in Newtonian and MOND-inspired gravitational potentials

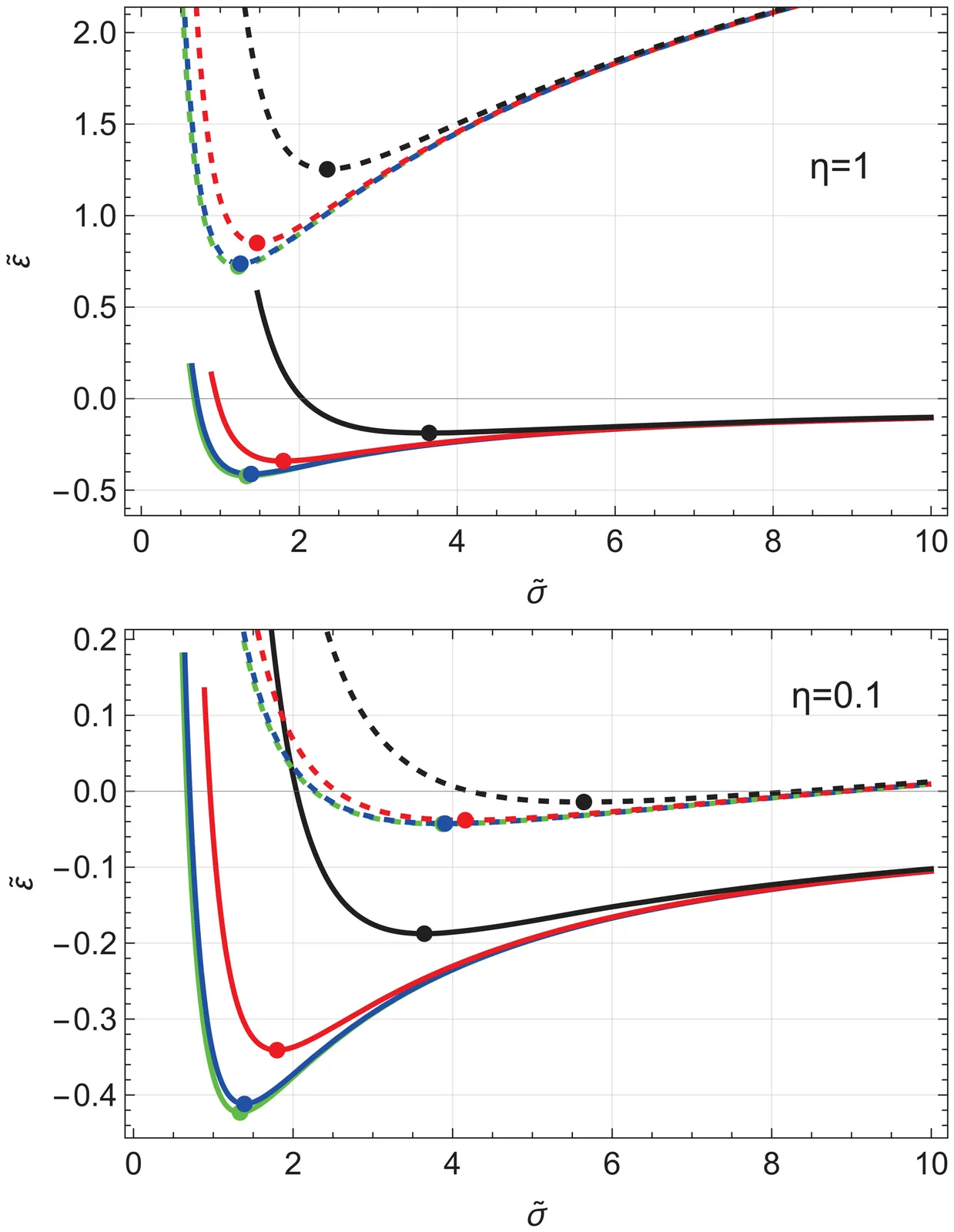
We analytically and numerically study the ground state and collective dynamics of Bose-Einstein condensates in two traps: a Newtonian potential and a logarithmic potential inspired by Modified Newtonian Dynamics (MOND). In the ground state, the MOND potential supports bound states only in the deep-MOND regime, where the condensate becomes significantly larger than its Newtonian counterpart. The size increases with repulsive coupling parameter $β$ in both potentials. A clear scaling law of the size with $β^{1/3}$ emerges in the MOND case and is confirmed numerically over a wide parameter range, while for the Newtonian potential no simple scaling law exists as the Thomas-Fermi approximation ceases to be valid. For the dynamics, we derive and solve equations for the monopole collective mode. The larger MOND-bound condensate oscillates at a lower frequency, which scales as $β^{-1/3}$ in the strong-interaction limit. These scaling laws provide insights for quantum-simulation experiments aiming to probe modified-gravity scenarios with cold atoms.

2601.01039Jan 2026

View

Numerical study of boson mixtures with multi-component continuous matrix product states

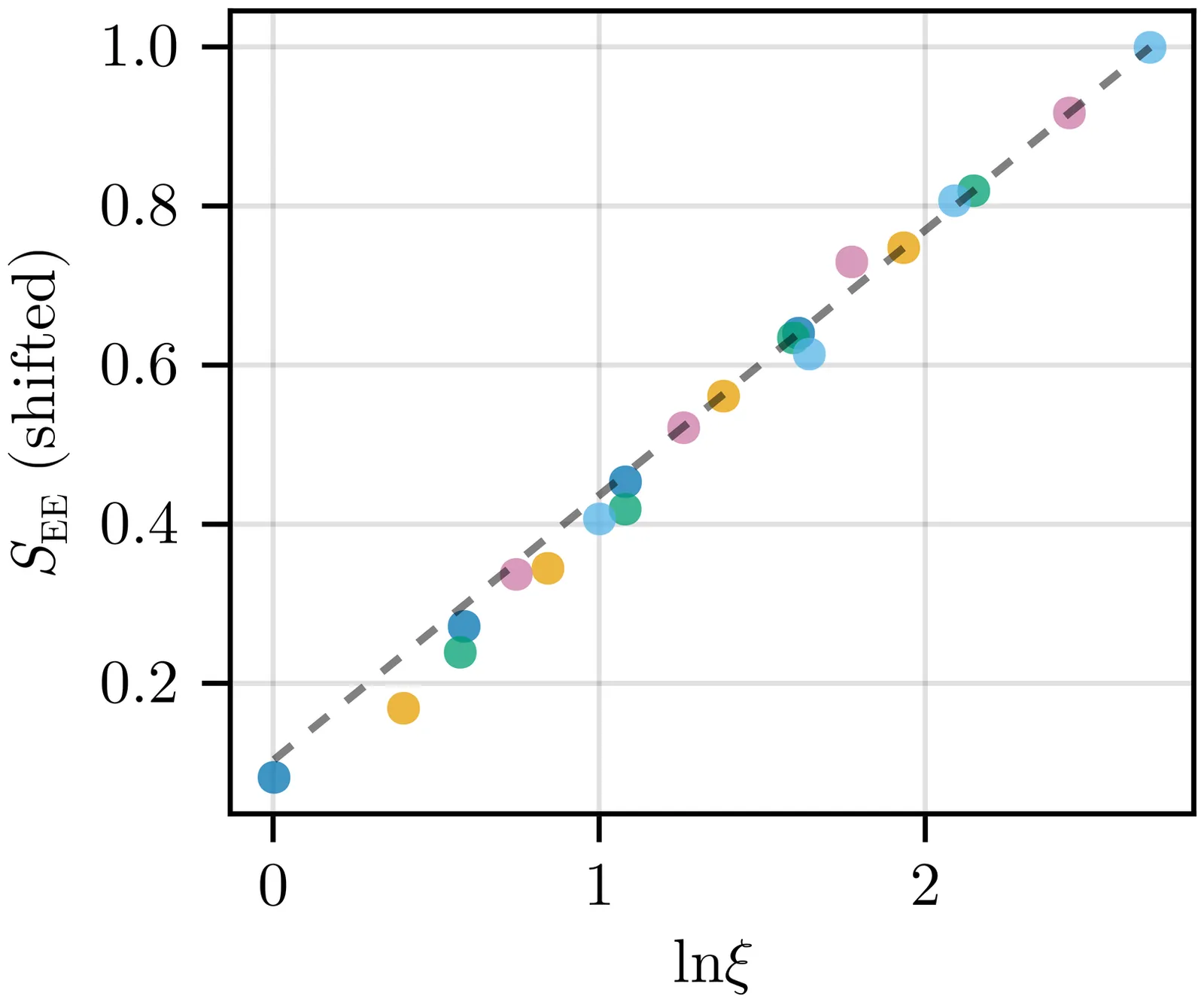
The continuous matrix product state (cMPS) ansatz is a promising numerical tool for studying quantum many-body systems in continuous space. Although it provides a clean framework that allows one to directly simulate continuous systems, the optimization of cMPS is known to be a very challenging task, especially in the case of multi-component systems. In this work, we have developed an improved optimization scheme for multi-component cMPS that enables simulations of bosonic quantum mixtures with substantially larger bond dimensions than previous works. We benchmark our method on the two-component Lieb-Liniger model, obtaining numerical results that agree well with analytical predictions. Our work paves the way for further numerical studies of quantum mixture systems using the cMPS ansatz.

2512.24998Dec 2025

View

Assembling a Bose-Hubbard superfluid from tweezer-controlled single atoms

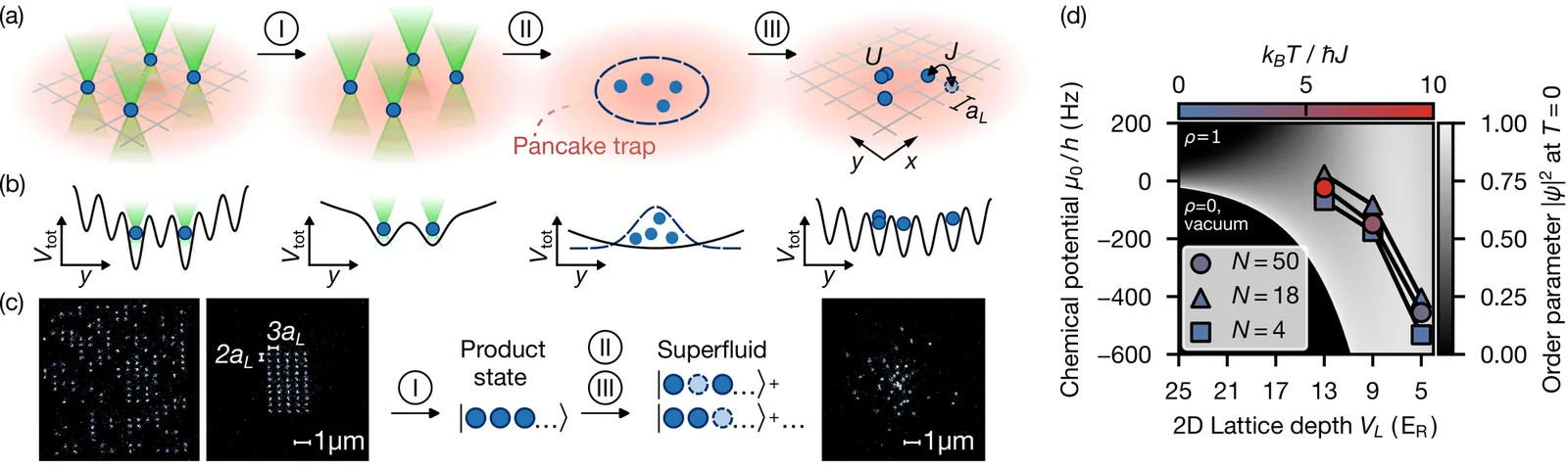
Quantum simulation relies on the preparation and control of low-entropy many-body systems to reveal the behavior of classically intractable models. The development of new approaches for realizing such systems therefore represents a frontier in quantum science. Here we experimentally demonstrate a new protocol for generating ultracold, itinerant many-body states in a tunnel-coupled two-dimensional optical lattice. We do this by adiabatically connecting a near-ground-state-cooled array of up to 50 single strontium-86 atoms with a Bose-Hubbard superfluid. Through comparison with finite-temperature quantum-Monte-Carlo calculations, we estimate that the entropy per particle of the prepared many-body states is approximately $2 k_B$, and that the achieved temperatures are consistent with a significant superfluid fraction. This represents the first time that itinerant many-body systems have been prepared from rearranged atoms, opening the door to bottom-up assembly of a wide range of neutral-atom and molecular systems.

2512.24374Dec 2025

View

Ergodicity breaking meets criticality in a gauge-theory quantum simulator

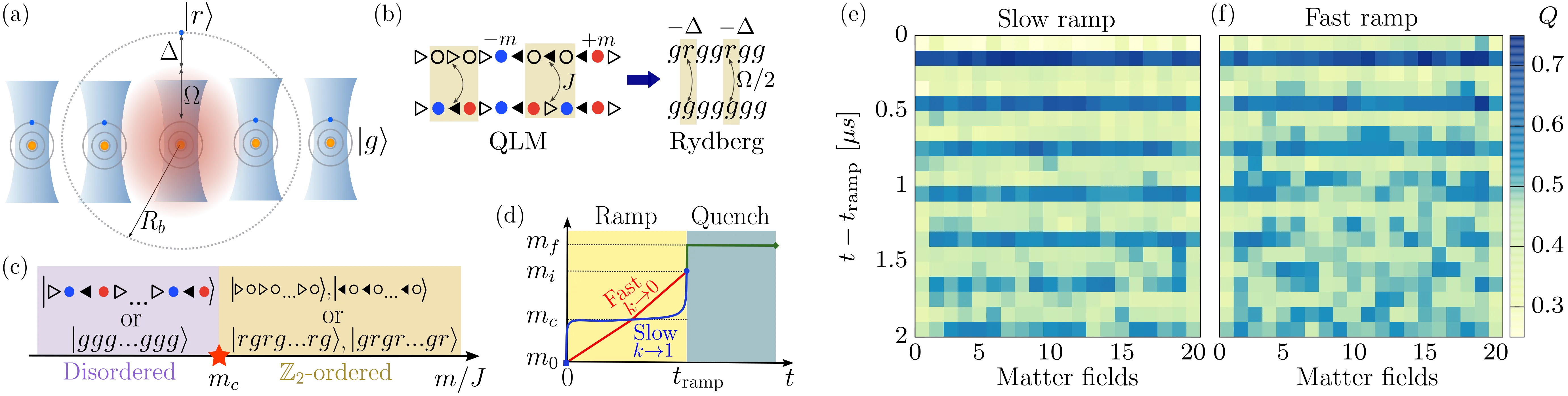
Recent advances in quantum simulations have opened access to the real-time dynamics of lattice gauge theories, providing a new setting to explore how quantum criticality influences thermalization and ergodicity far from equilibrium. Using QuEra's programmable Rydberg atom array, we map out the dynamical phase diagram of the spin-1/2 U(1) quantum link model in one spatial dimension by quenching the fermion mass. We reveal a tunable regime of ergodicity breaking due to quantum many-body scars, manifested as long-lived coherent oscillations that persist across a much broader range of parameters than previously observed, including at the equilibrium phase transition point. We further analyze the electron-positron pairs generated during state preparation via the Kibble-Zurek mechanism, which strongly affect the post-quench dynamics. Our results provide new insights into nonthermal dynamics in lattice gauge theories and establish Rydberg atom arrays as a powerful platform for probing the interplay between ergodicity breaking and quantum criticality.

2512.23794Dec 2025

View

Fast collisional $\sqrt{\mathrm{SWAP}}$ gate for fermionic atoms in an optical superlattice

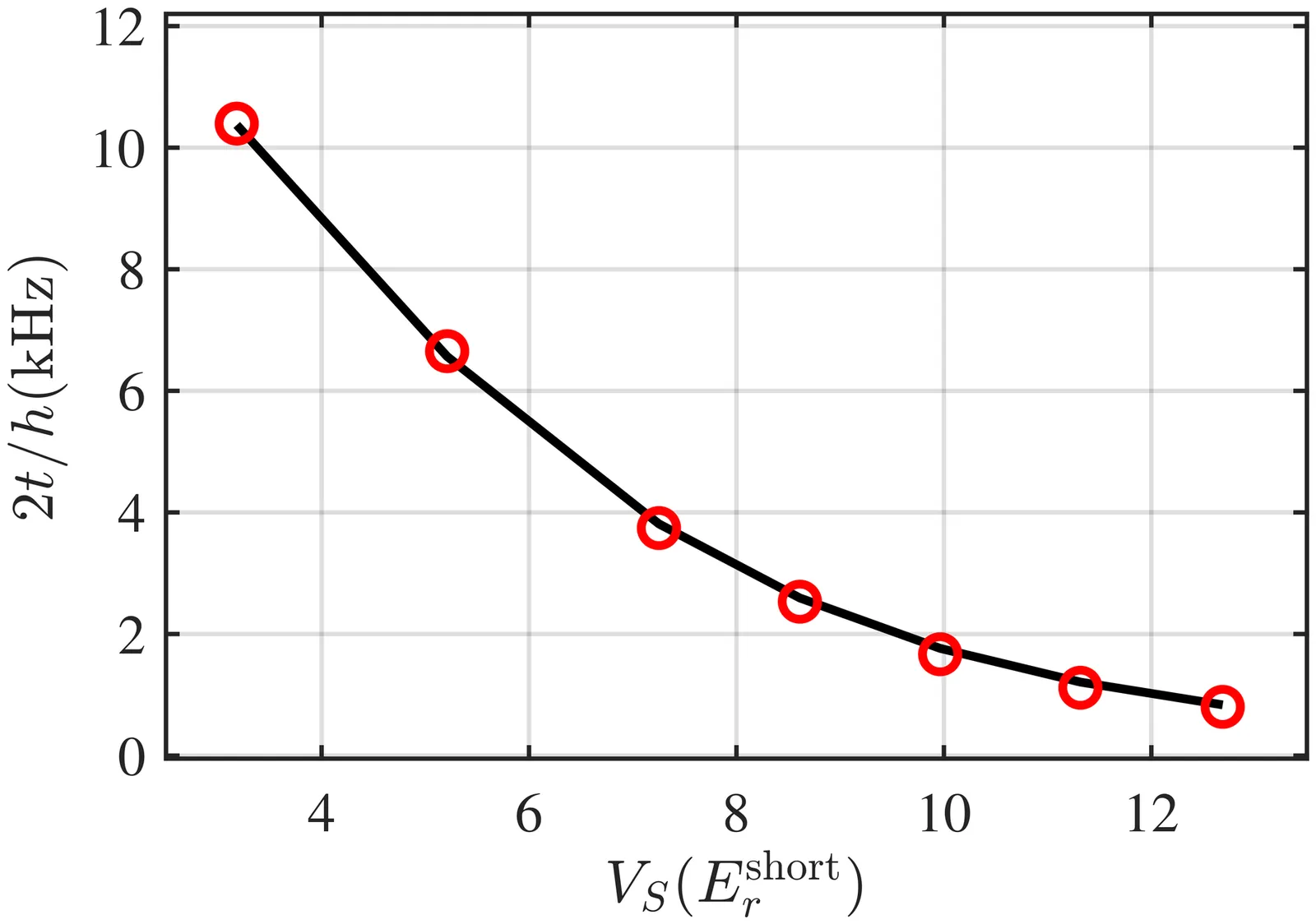
Collisional gates in optical superlattices have recently achieved record fidelities, but their operation times are typically limited by tunneling. Here we propose and analyze an alternative route to a fast $\sqrt{\mathrm{SWAP}}$ gate for two fermionic atoms in an optical superlattice based on optimized, time-dependent control of the short and long lattice depths. The gate is implemented by transiently releasing the atoms into a quasi-harmonic confinement centered between the two sites. With an appropriately chosen contact interaction strength, a controlled collision accumulates the exchange phase required for $\sqrt{\mathrm{SWAP}}$ and generates entanglement. We employ a continuum, time-dependent Schrödinger-equation simulation that goes beyond a two-site Fermi--Hubbard description and benchmark it against experimentally implemented tunneling-based protocols, reproducing the observed single-particle tunneling and spin-exchange dynamics. For experimentally accessible lattice depths, we find that the proposed gate operates in $\sim 21\,μ\mathrm{s}$, more than an order of magnitude faster than tunneling-based implementations, while achieving fidelities $\gtrsim 99\%$. We further analyze sensitivity to lattice-depth variations and show that a composite sequence improves robustness. Our results establish fast, collision-mediated entangling gates in superlattices as a promising building block for scalable neutral-atom quantum computation.

2512.22569Dec 2025

View

Asymmetric and chiral dynamics of two-component anyons with synthetic gauge flux

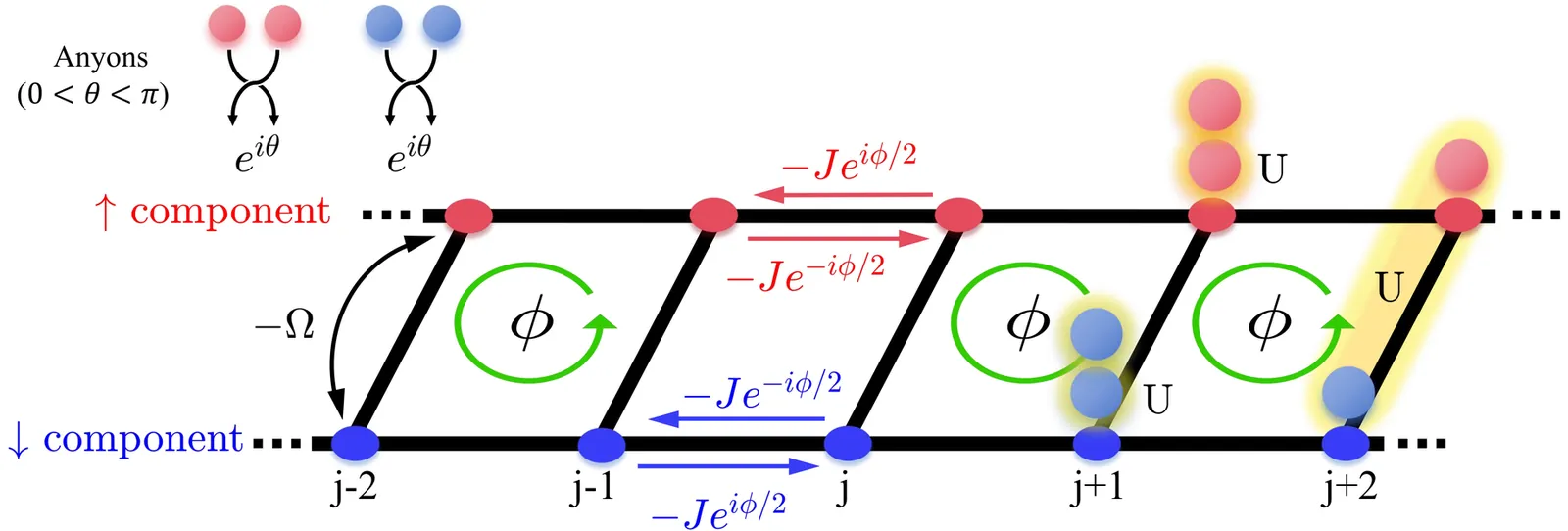
In this work, we investigate the non-equilibrium dynamics in a one-dimensional two-component anyon-Hubbard model, which can be mapped to an extended Bose-Hubbard ladder with density-dependent hopping phase and synthetic gauge flux. Through numerical simulations of two-particle dynamics and the symmetry analysis, we reveal the asymmetric transport with broken inversion symmetry and two dynamical symmetries in the expansion dynamics. The expansion of two-component anyons is dynamically symmetric under spatial inversion and component flip, when the sign of anyonic statistics phase or the signs of gauge flux and interaction are changed. In the non-interacting case, we show the dynamical suppression induced by both the statistics phase and gauge flux. In the interacting case, we demonstrate that both chiral and antichiral dynamics can be exhibited and tuned by the statistics phase and gauge flux. The dynamical phase regimes with respect to the chiral-antichiral dynamics are obtained. These findings highlight the rich dynamical phenomena arising from the interplay of anyonic exchange statistics, synthetic gauge fields, and interactions in multi-component anyons.

2512.19139Dec 2025

View

Momentum correlations of the Hawking effect in a quantum fluid

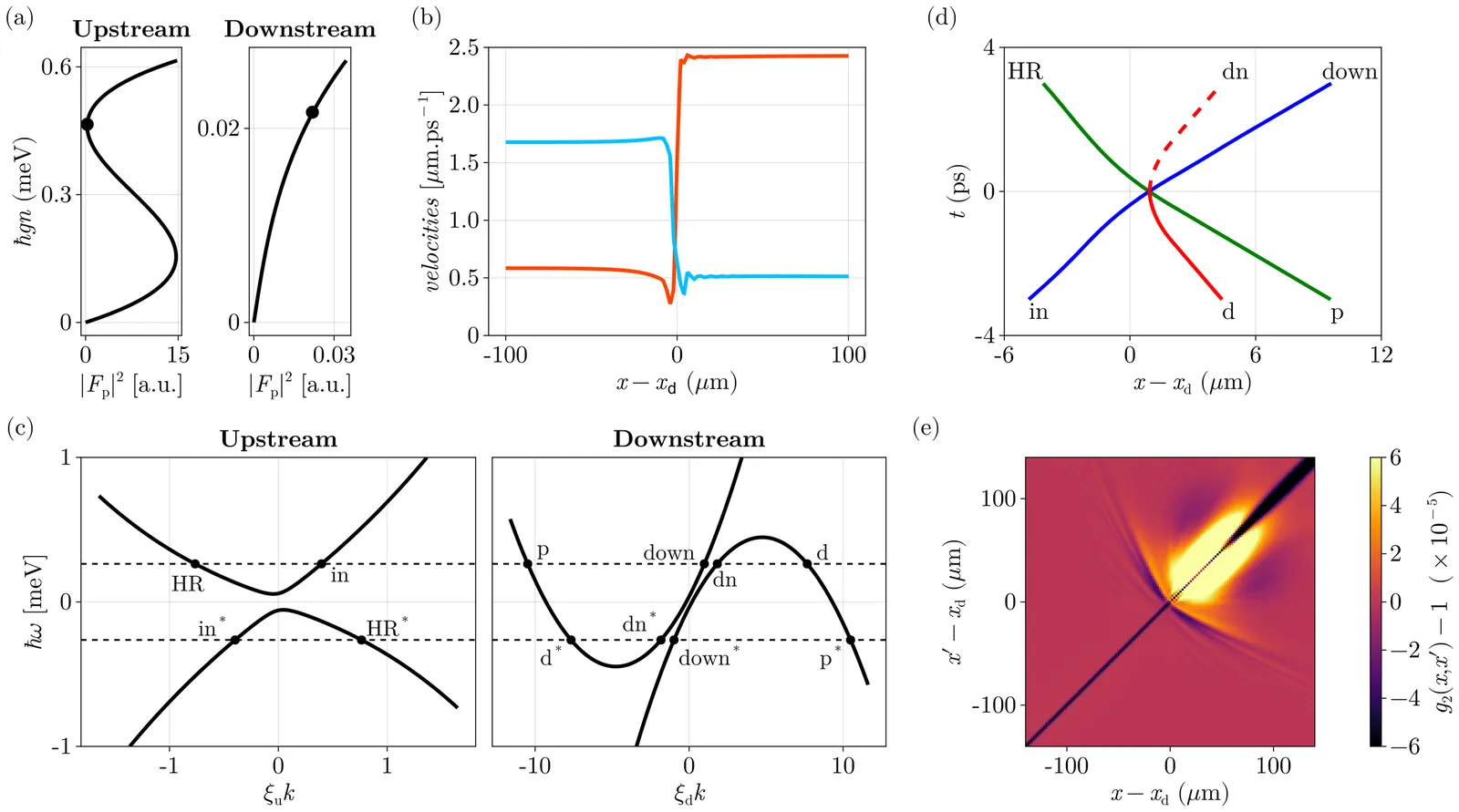
The Hawking effect -- the spontaneous emission of correlated quanta from horizons -- can be observed in laboratory systems where an acoustic horizon forms when a fluid transitions from subcritical to supercritical flow. Although most theoretical and experimental studies have relied on real-space observables, the frequency-dependent nature of the Hawking process motivates a momentum-space analysis to access its spectral structure and entanglement features. Here, we numerically compute the momentum-space two-point correlation function in a quantum fluid using the truncated Wigner approximation, a general method applicable to both conservative and driven-dissipative systems. We consider a polaritonic fluid of light in a realistic configuration known to yield strong real-space correlations between Hawking, partner, and witness modes. We find signatures that are directly accessible in state-of-the-art experiments and offer a robust diagnostic of spontaneous emission. Our results form the basis for a new theoretical framework to assess a variety of effects, such as quasi-normal mode emission or modifications of the horizon structure on the Hawking spectrum.

2512.17807Dec 2025

View

The crossover from classical to quantum transport in a weakly-interacting Fermi gas

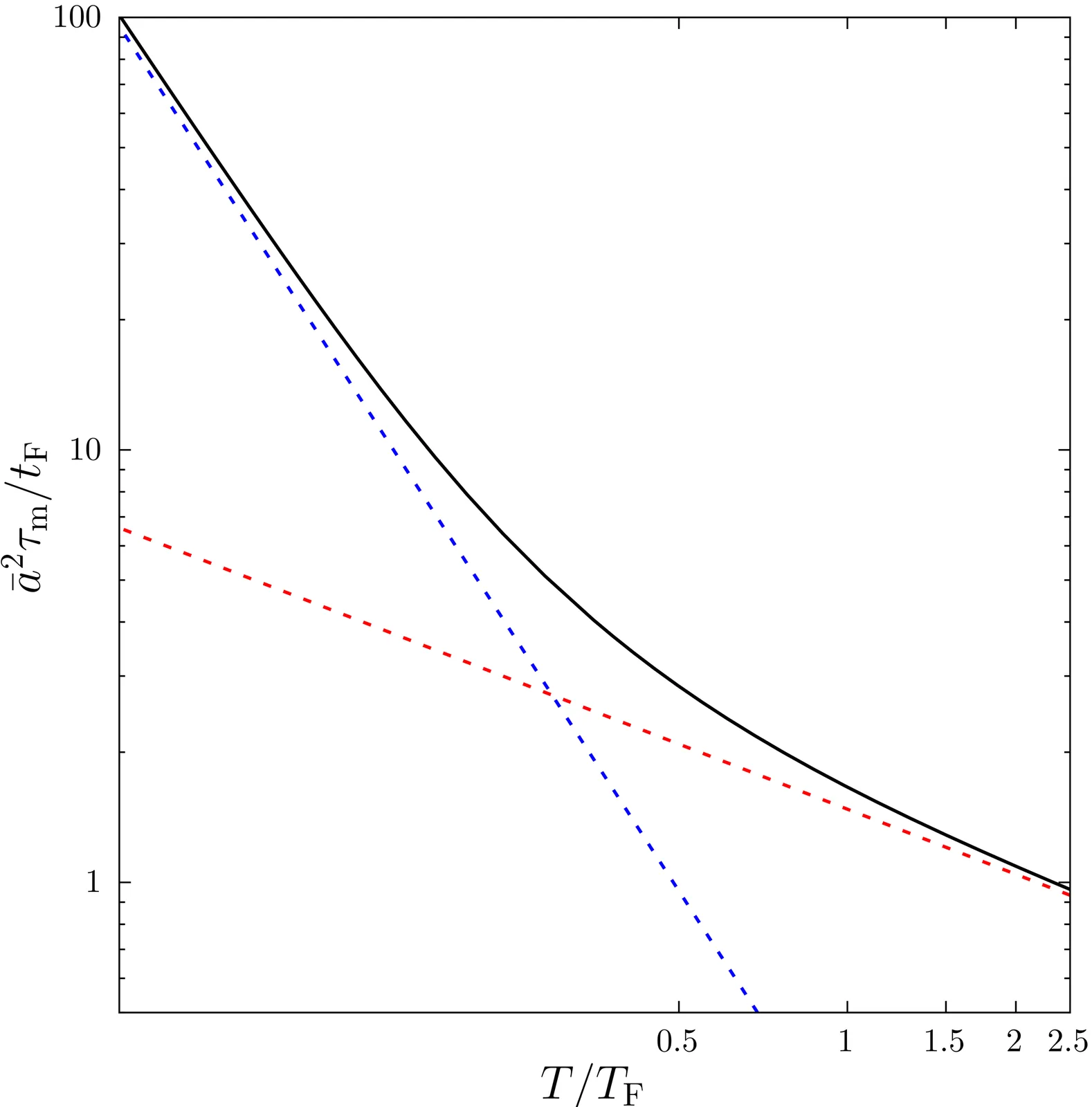
We present an exact solution of the quantum kinetic equation of a weakly interacting Fermi gas in the crossover from the degenerate Fermi-liquid regime to the classical Boltzmann gas. We construct families of orthogonal polynomials tailored to each angular momentum channel, enabling a fast and systematically improvable decomposition of the phase-space distribution. This approach yields accurate, non-variational predictions for the shear viscosity, thermal diffusivity, and spin diffusivity to leading order in the scattering length. We demonstrate that the commonly used relaxation-time approximation fails dramatically at low temperature--by up to 25%. Our method provides a numerically efficient framework for benchmarking transport in strongly correlated regimes and for simulating the kinetics of quantum gases beyond hydrodynamics.

2512.17379Dec 2025

View

Correlated many-body quantum dynamics of the Peregrine soliton

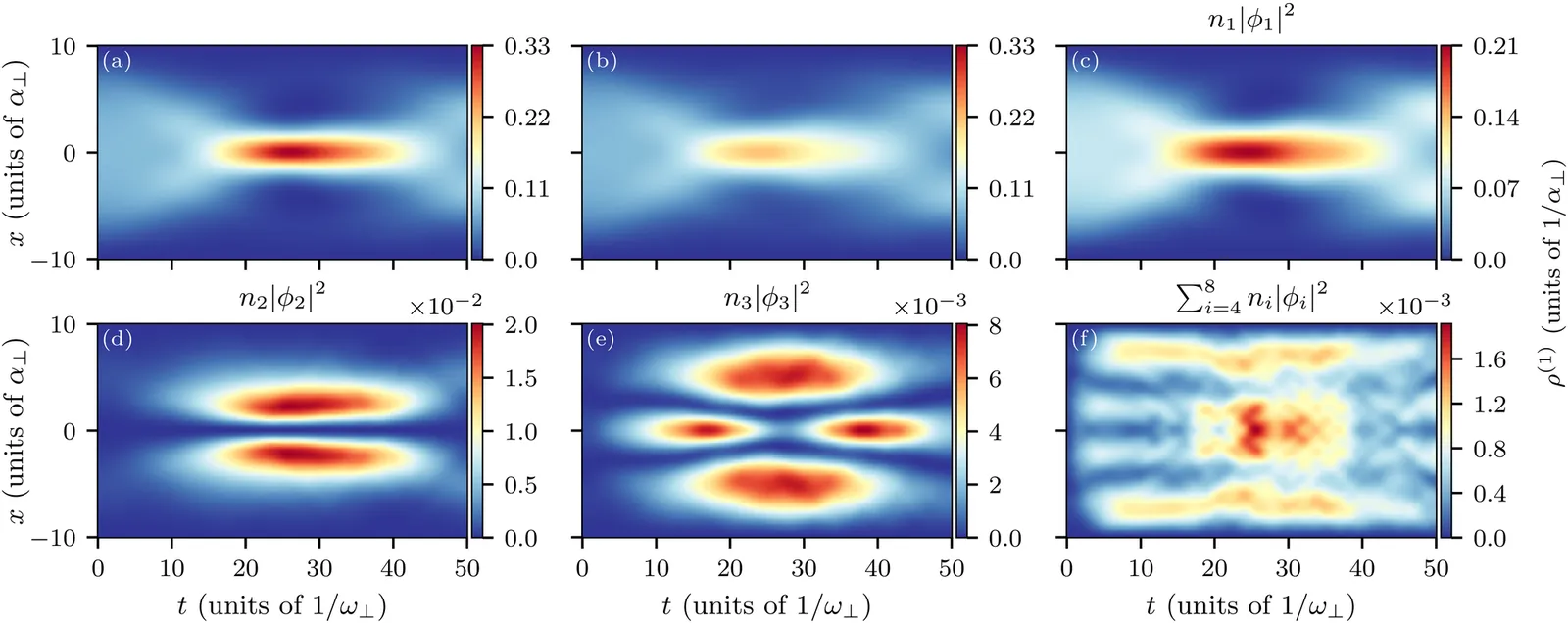
We explore the correlated dynamics underlying the formation of the quantum Peregrine soliton, a prototypical rogue-wave excitation, utilizing interaction quenches from repulsive to attractive couplings in an ultracold bosonic gas confined in a one-dimensional box trap. The latter emulates the so-called semi-classical initial conditions and the associated gradient catastrophe scenario facilitating the emergence of a high-density, doubly localized waveform. The ensuing multi-orbital variant of the Peregrine soliton features notable deviations from its mean-field sibling, including a reduced peak amplitude, wider core, absence of the side density dips, and earlier formation times. Moreover, Peregrine soliton generation yields coherence losses, while experiencing two-body bunching within each of its sides which show anti-bunching between each other. Controllable seeding of the Peregrine soliton is also demonstrated by tuning the atom number or the box length, while reducing the latter favors the generation of the time-periodic Kuznetsov-Ma breather. Our results highlight that correlations reshape the morphology of rogue-waves in the genuinely quantum, non-integrable realm, while setting the stage for the emergent field of quantum dispersive hydrodynamics.

2512.16031Dec 2025

View

Two-Body Kapitza-Dirac Scattering of One-Dimensional Ultracold Atoms

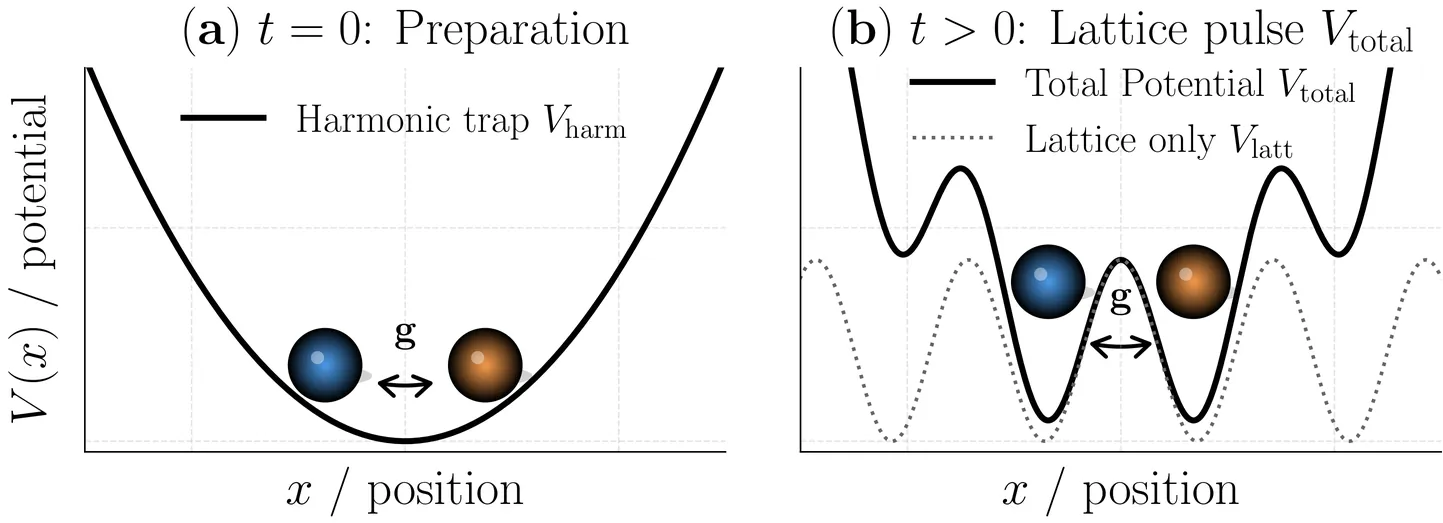
Kapitza-Dirac scattering, the diffraction of matter waves from a standing light field, is widely utilized in ultracold gases, but its behavior in the strongly interacting regime is an open question. Here we develop a numerically-exact two-body description of Kapitza-Dirac scattering for two contact-interacting atoms in a one-dimensional harmonic trap subjected to a pulsed optical lattice, enabling us to obtain the numerically exact dynamics. We map how interaction strength, lattice depth, lattice wavenumber, and pulse duration reshape the diffraction pattern, leading to an interaction-dependent population redistribution in real and momentum-space. By comparing the exact dynamics to an impulsive sudden-approximation description, we delineate the parameter regimes where it remains accurate and those, notably at strong attraction and small lattice wavenumber, where it fails. Our results provide a controlled few-body benchmark for interacting Kapitza-Dirac scattering and quantitative guidance for Kapitza-Dirac-based probes of ultracold atomic systems.

2512.15260Dec 2025

View

Localization from Infinitesimal Kinetic Grading: Critical Scaling and Kibble-Zurek Universality

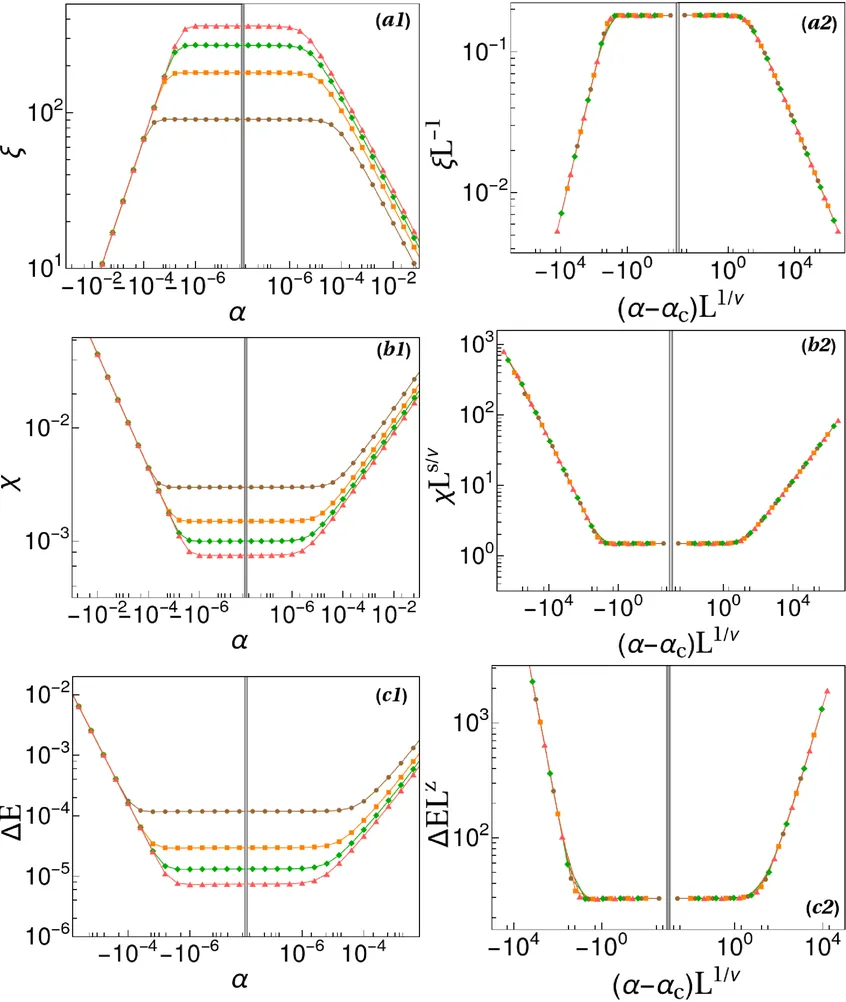
We study a one-dimensional lattice model with site-dependent nearest-neighbor hopping amplitudes that follow a power-law profile. The hopping variation is controlled by a grading exponent, $α$, which serves as the tuning parameter of the system. In the thermodynamic limit, the ground state becomes localized as $|α| \to 0$, signaling the presence of a critical point characterized by a diverging localization length. Using exact diagonalization, we perform finite-size scaling analysis and extract the associated critical exponent governing this divergence, revealing a universality class distinct from well-known Anderson, Aubry-Andre, and Stark localization. To further characterize the critical behavior, we analyze the inverse participation ratio, the energy gap between the ground and first excited states, and the fidelity susceptibility. We also investigate nonequilibrium dynamics by linearly ramping the hopping profile at various rates and tracking the evolution of the localization length and the inverse participation ratio. The Kibble-Zurek mechanism successfully captures the resulting dynamics using the critical exponents obtained from the static scaling analysis. Our results demonstrate a clean, disorder-free route to localization and provide a tunable platform relevant to photonic lattices and ultracold atom arrays with engineered hopping profiles.

2512.15795Dec 2025

View

From few- to many-body physics: Strongly dipolar molecular Bose-Einstein condensates and quantum fluids

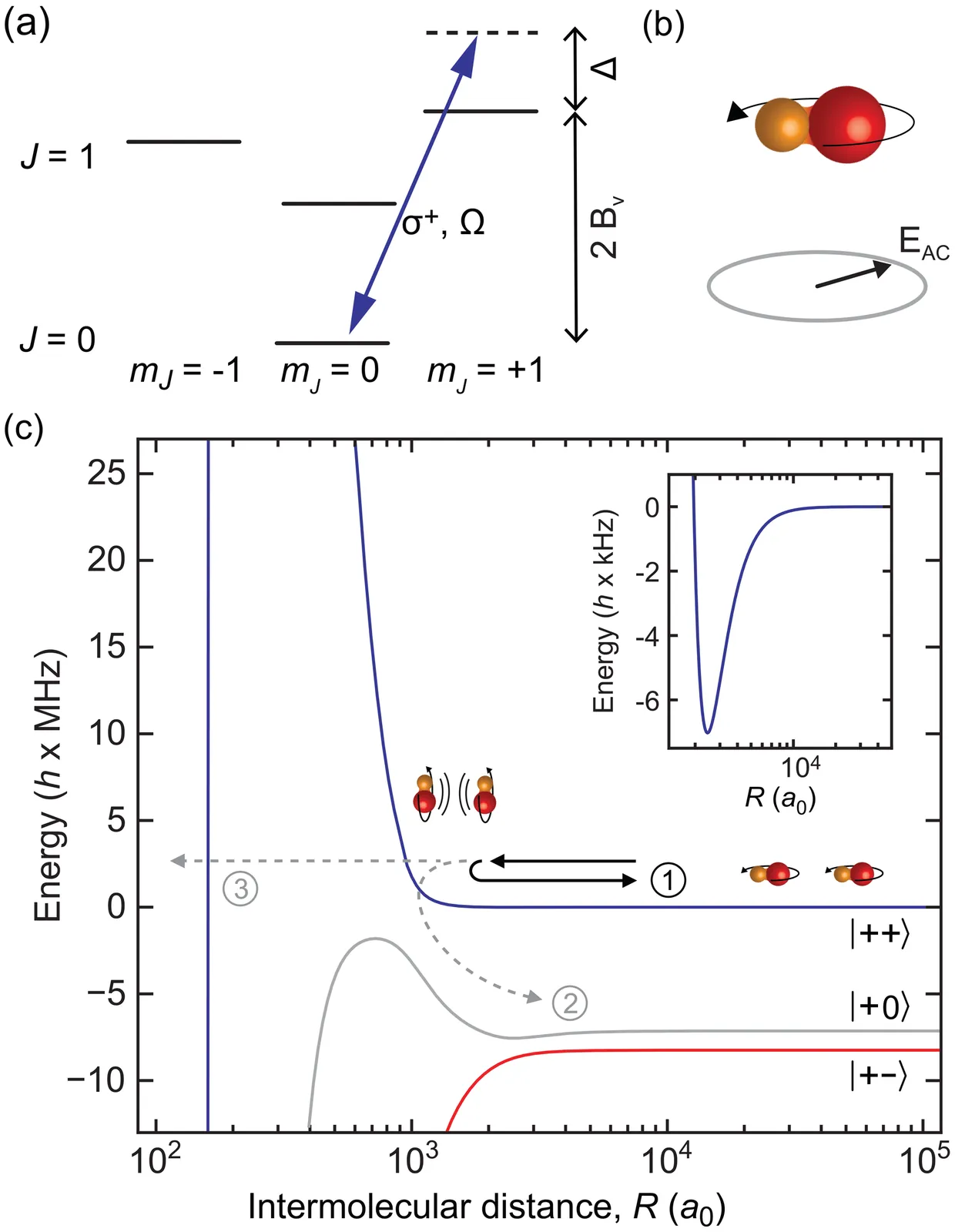
Recent advances in molecular cooling have enabled the realization of strongly dipolar Bose-Einstein condensates (BECs) of molecules, and BECs of many different molecular species may become experimentally accessible in the near future. Here, we explore the unique properties of such BECs and the new insights they may offer into dipolar quantum fluids and many-body physics. We explore which parameter regimes can realistically be achieved using currently available experimental techniques, discuss how to implement these techniques, and outline which molecular species are particularly well suited to explore exotic new states of matter. We further determine how state-of-the-art beyond mean-field theories, originally developed for weakly dipolar magnetic gases, can be pushed to their limits and beyond, and what other long-standing questions in the field of dipolar physics may realistically come within reach using molecular systems.

2512.14511Dec 2025

View

Dipolar quantum gases: from 3D to Low dimensions

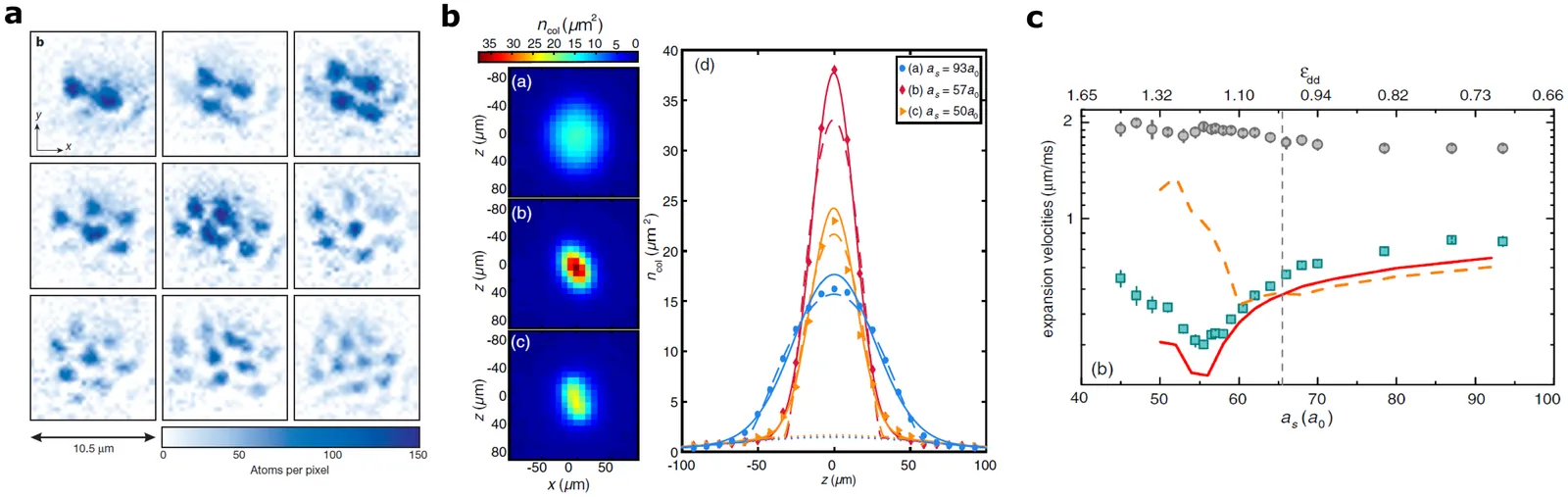
Dipolar quantum gases, encompassing atoms and molecules with significant dipole moments, exhibit unique long-range and anisotropic dipole-dipole interactions (DDI), distinguishing them from systems dominated by short-range contact interactions. This review explores their behavior across dimensions, focusing on magnetic atoms in quasi-2D in comparison to 3D. In 3D, strong DDI leads to phenomena like anisotropic superfluidity, quantum droplets stabilized by Lee-Huang-Yang corrections, and supersolid states with density modulations. In 2D, we discuss a new scenario where DDI induces angle-dependent Berezinskii-Kosterlitz-Thouless transitions and potential supersolidity, as suggested by recent experimental realizations of strongly dipolar systems in quasi-2D geometries. We identify key challenges for future experimental and theoretical work on strongly dipolar 2D systems. The review concludes by highlighting how these unique 2D dipolar systems could advance fundamental research as well as simulate novel physical phenomena.

2512.14268Dec 2025

View

Quantum fields in a cold atomic simulator: relaxation and phase locking in tunnel-coupled 1D bosonic quasi-condensates

We consider a prime example of simulating interacting relativistic QFT with cold atoms: the realisation of the sine-Gordon model by tunnel-coupled quasi-1D Bose gases. While experiments have shown that it can realise the sine-Gordon model in equilibrium, studies of non-equilibrium dynamics have revealed a phase-locking behaviour that stands in contrast to predictions from sine-Gordon field theory. Here, we examine a one-dimensional field-theoretic model of the system and find that the phase-locking behaviour can be understood in terms of the presence of the longitudinal harmonic trap, and that the additional degrees of freedom known to be present in the experiment do not appear to play a significant role. Therefore, the experimental setup provides a good simulator of the sine-Gordon quantum field theory, even out of equilibrium, if the inhomogeneous background induced by the trap is taken into account. Furthermore, our results support the idea that modifying the longitudinal trap to a box shape should result in agreement with standard sine-Gordon dynamics. The main remaining open issues are to account for 3D corrections and model the effect of the boundaries.

2512.13901Dec 2025

View

Quasiparticle projection method for dynamically unstable Bose-Einstein condensates

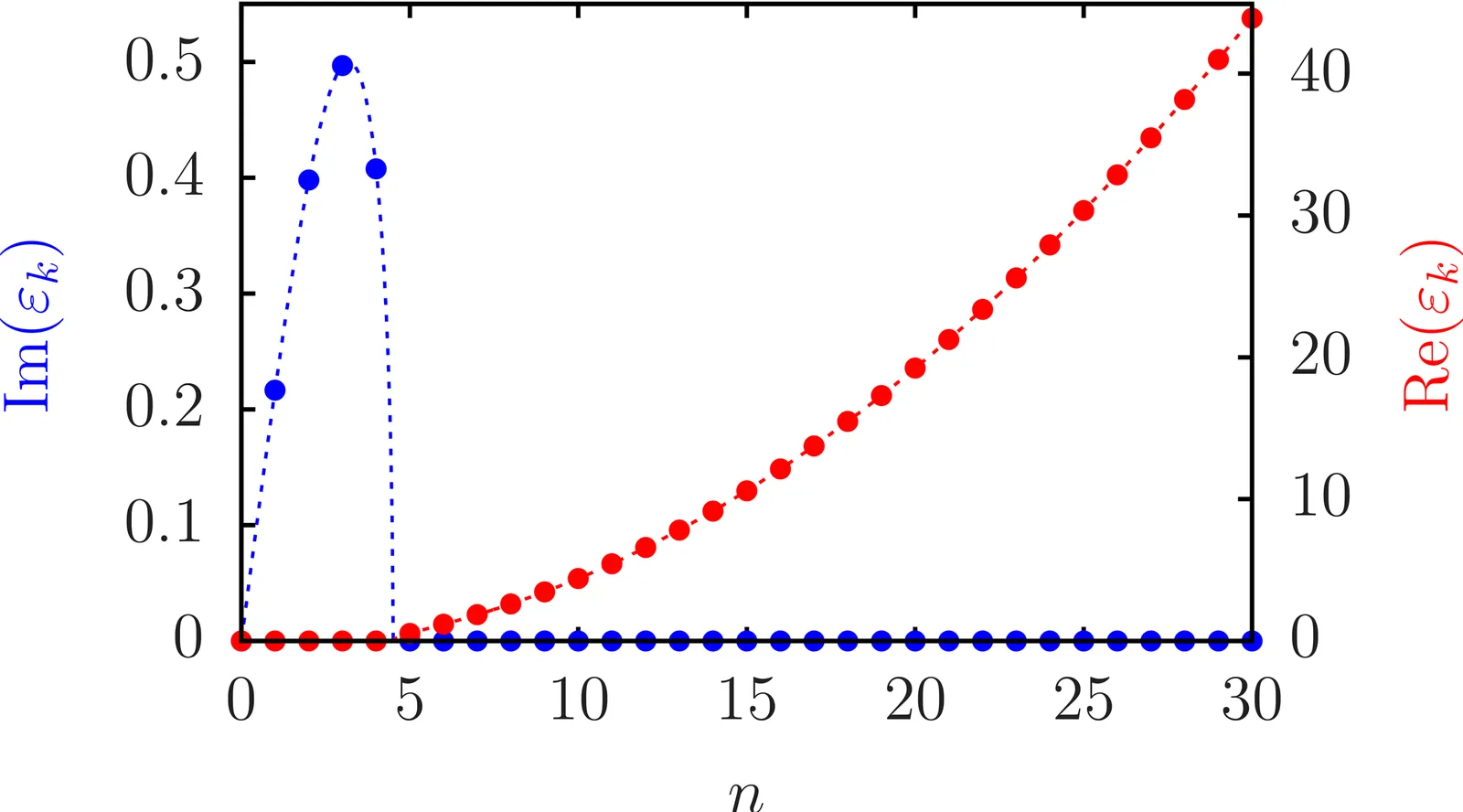
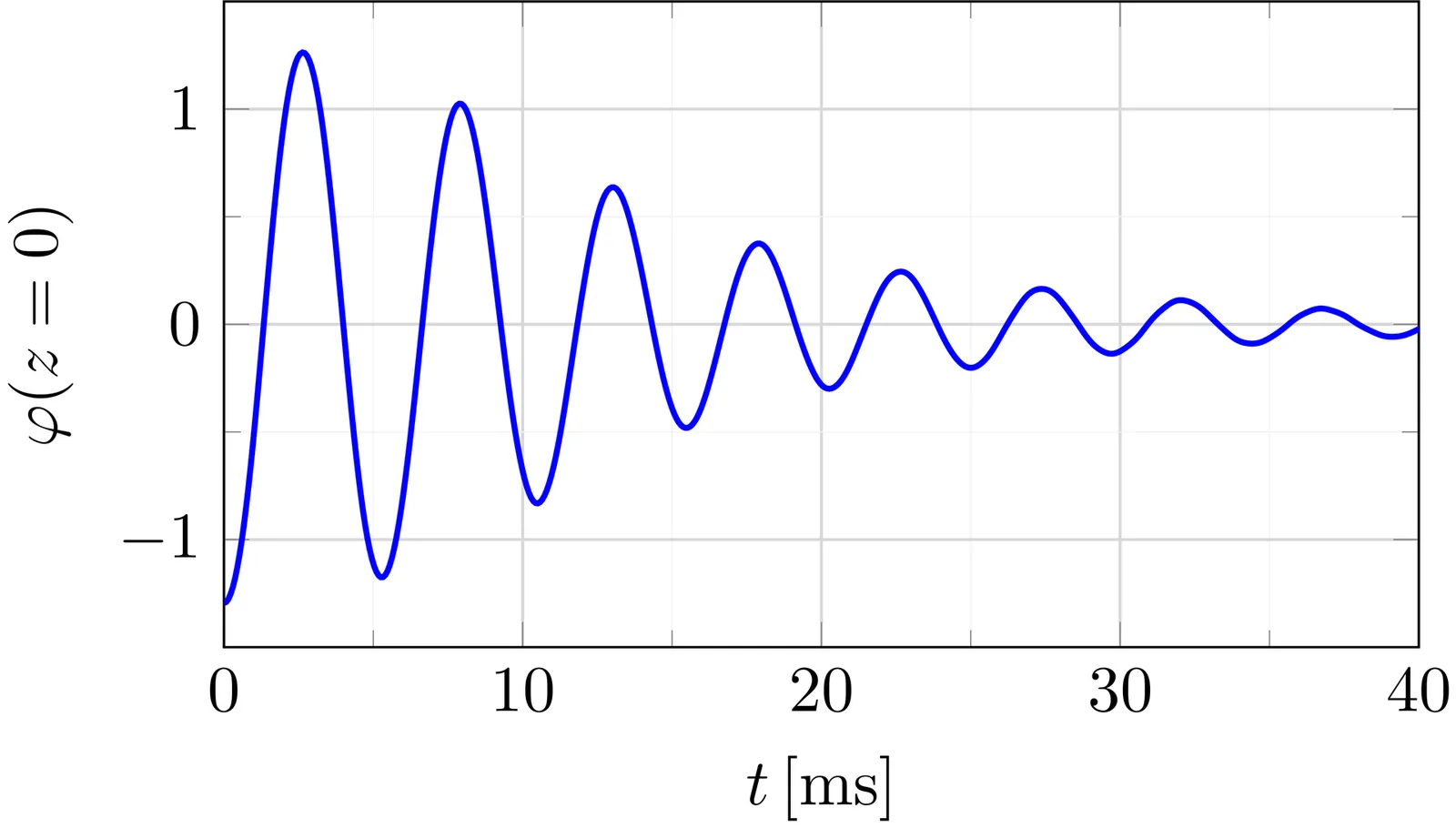
We present a general formalism for performing a time-dependent Bogoliubov analysis of a dynamically unstable Bose-Einstein condensate, which extends the quasiparticle projection method of Morgan et al. [Phys. Rev. A 57, 3818 (1998)] to cases with a complex spectrum. By introducing the proper left eigenvectors associated with each regime, we construct a biorthogonal basis. While the usual Bogoliubov normalization $\langle u | u \rangle - \langle v | v \rangle = 1$ may not hold in this basis, it still allows for a complete mode decomposition and an accurate reconstruction of arbitrary perturbations over time. This approach extends the applicability of the Bogoliubov framework beyond the stable regime, providing a consistent analysis of the time evolution of unstable condensates. As a proof of concept, we apply the method to a one-dimensional condensate with attractive interactions, which is dynamically unstable and evolves into nonstationary localized structures seeded by small perturbations.

2512.13847Dec 2025

View

Interferometric probe for the zeros of the many-body wavefunction

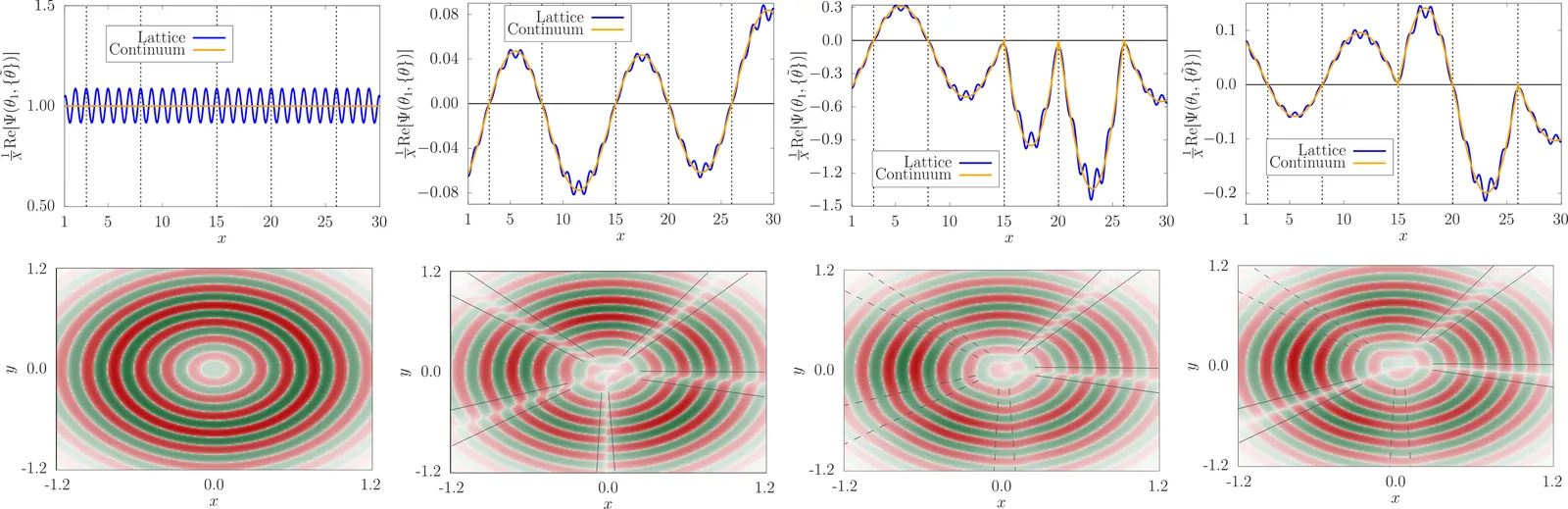
The nodal surfaces of the many-body wavefunction are fundamental geometric features that encode critical information regarding particle statistics and their interaction. Directly probing these structures, particularly in correlated quantum systems, remains a significant experimental challenge. Here, we provide rigorous results on the structure of the many-body wavefunction and propose to use an interferometric technique to probe its zeros in ultra-cold atomic systems. Specifically, we refer to the so-called heterodyne interferometric reconstruction of the phase of the many-body wavefunction. We prove that the sought nodal surfaces show up as specific discontinuities in the interference fringes. Following Leggett, both `symmetry-dictated' nodal surfaces, due to particle statistics, and `non-symmetry dictated' nodal surfaces emerging from interaction effects, can be probed. We demonstrate how the spin degrees of freedom, effectively modifying the structure of the nodal surfaces of the many-body wavefunction, leave distinct fingerprints in the resulting interference pattern. Our work addresses important features of the structure of the many-body wavefunction that are broadly relevant for quantum science ranging from conceptual aspects to computational questions of extended systems and quantum simulation.

2512.13795Dec 2025

View

Self-consistent effective field theory to nonuniversal Lee-Huang-Yang term in quantum droplets

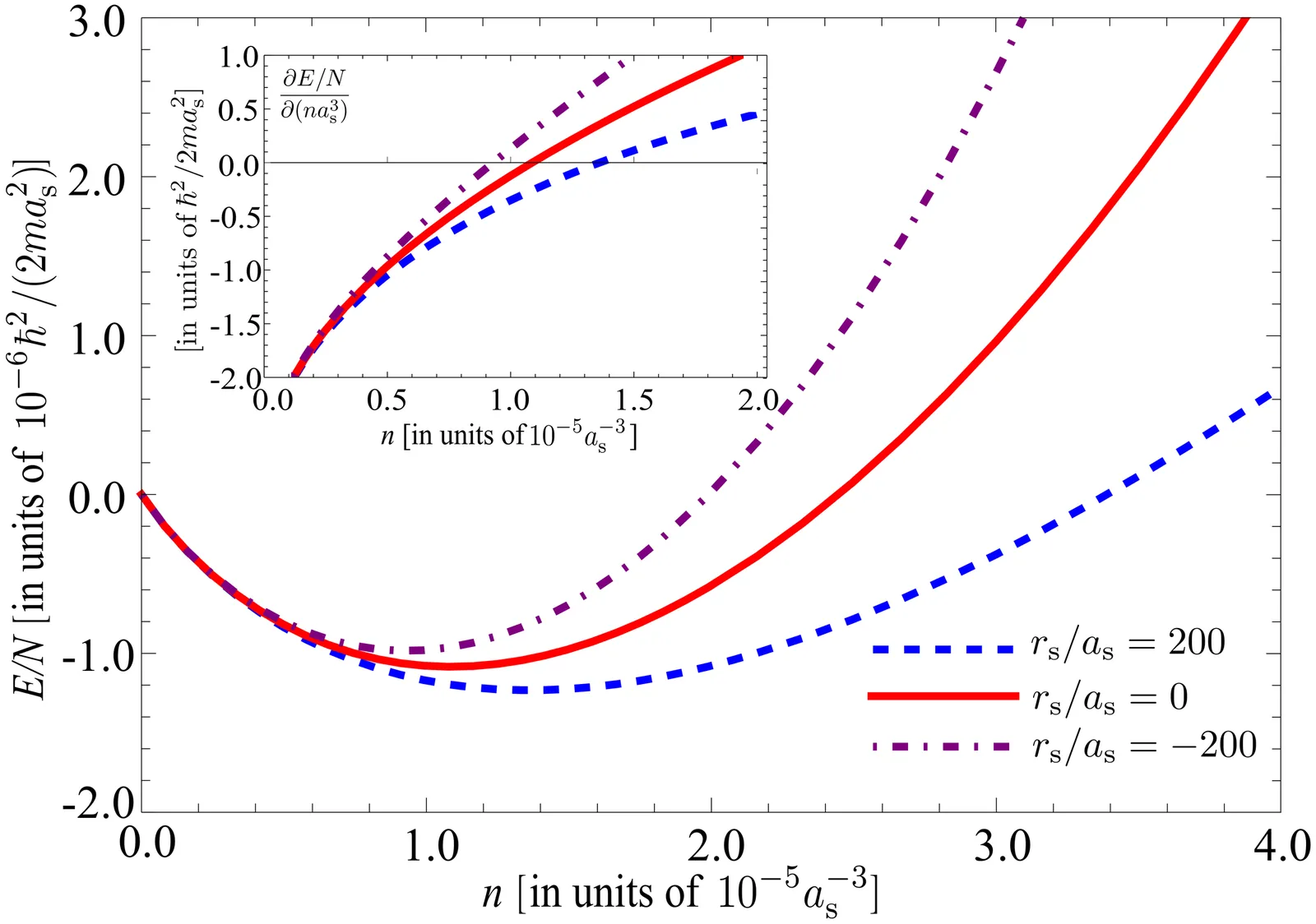
Quantum droplets (QDs) in weakly interacting ultracold quantum gases are typically characterized by mean-field theories incorporating Lee-Huang-Yang (LHY) quantum fluctuations under simplified zero-range interaction assumptions. However, bridging these models to broader physical regimes like superfluid helium requires precise understanding of short-range interatomic interactions. Here, we investigate how finite-range interactions--next-order corrections to zero-range potentials--significantly alter QDs mechanics. Using a consistent effective theory, we derive an analytical equation of state (EOS) for three-dimensional bosonic mixtures under finite-range interactions at zero temperature. Leveraging the Hubbard-Stratonovich transformation, we demonstrate that interspecies attraction facilitates bosonic pairing across components characterized by the non-perturbative parameter of $Δ$, leading to nonuniversal LHY terms that encode short-range interaction details while recovering previous universal QDs EOS in the zero-range limit. Extending superfluid hydrodynamic equations for two-component systems, we predict fractional frequency shifts in breathing modes induced by these nonuniversal terms. Experimental observation of these shifts would reveal critical insights into QDs dynamics and interatomic potential characteristics.

2512.11513Dec 2025

View

Page 1 of 13