Nuclear Theory

arXiv:nucl-th

Theory of nuclear structure and reactions.

Looking for a broader view? This category is part of:

Trending in Nuclear Theory

Toward $\textit{Ab Initio}$ Quantum Simulations of Atomic Nuclei Using Noisy Qubits

Quantum computers are expected to provide a ultimate solver for quantum many-body systems, although it is a tremendous challenge to achieve that goal on current noisy quantum devices. This work illustrated quantum simulations of ab initio no-core shell model calculations of $^3$H with chiral two-nucleon and three-nucleon forces. The measurement costs are remarkably reduced by using the general commutativity measurement together with the asymptotic optimization. In addition, the noise causes serious contaminations of configurations with undesired particle numbers, and the accuracies are much improved by applying the particle number projected measurement. By tackling the efficiency and noise issues, this work demonstrated a substantial step toward ab initio quantum computing of atomic nuclei.

2601.00315

Jan 2026Nuclear Theory

Leptophilic Interactions in Nuclear Energy Density Functional Theory

We develop a unified theoretical framework that embeds a light leptophilic vector boson into nuclear energy density functional (EDF) theory. Starting from an underlying leptophilic gauge interaction, the mediator is integrated out in the static limit, yielding an effective current--current interaction that couples proton and lepton densities. This interaction is incorporated self-consistently into relativistic mean-field equations, defining a leptophilic extension of conventional nuclear EDFs. The resulting leptophilic EDF induces correlated modifications of proton and lepton chemical potentials, directly affecting beta equilibrium in dense matter. In uniform matter, these effects lead to percent-level changes in the proton fraction, symmetry energy, and equation of state within phenomenologically allowed parameter ranges. In finite nuclei, the modified proton mean field generates shifts of $10^{-3}$--$10^{-2}\,\mathrm{fm}$ in neutron-skin thicknesses, comparable to current experimental sensitivities. Our results demonstrate that light leptophilic interactions leave coherent and experimentally accessible imprints on both nuclear structure and dense-matter observables. The framework introduced here provides a controlled and realistic extension of nuclear EDF theory, enabling nuclear systems to serve as laboratories for probing new physics in the leptonic sector.

2512.11770

Dec 2025Nuclear Theory

Related categories:

Nuclear Experiment

385 papers

A Universal Upper Bound on the Pressure-to-Energy Density Ratio in Neutron Stars

The equation-of-state (EOS) parameter $φ\equiv P/\varepsilon$, defined as the ratio of pressure to energy density, encapsulates the fundamental response of matter under extreme compression. Its value at the center of the most massive neutron star (NS), $\x \equiv φ_{\rm c} = P_{\rm c}/\varepsilon_{\rm c}$, sets a universal upper bound on the maximum denseness attainable by any form of visible matter anywhere in the Universe. Remarkably, owing to the intrinsically nonlinear structure of the EOS in General Relativity (GR), this bound is forced to lie far below the naive Special Relativity (SR) limit of unity. In this work, we refine the theoretical upper bound on $\x$ in a self-consistent manner by incorporating, in addition to the causality constraint from SR, the mass-sphere stability condition associated with the mass evolution pattern in the vicinity of the NS center. This condition is formulated within the intrinsic-and-perturbative analysis of the dimensionless Tolman--Oppenheimer--Volkoff equations (IPAD-TOV) framework. The combined constraints yield an improved bound, $\x \lesssim 0.385$, which is slightly above but fully consistent with the previously derived causal-only limit, $\x \lesssim 0.374$. We further derive an improved scaling relation for NS compactness and verify its universality across a broad set of 284 realistic EOSs, including models with first-order phase transitions, exotic degrees of freedom, continuous crossover behavior, and deconfined quark cores. The resulting bound on $\x$ thus provides a new, EOS-independent window into the microphysics of cold superdense matter compressed by strong-field gravity in GR.

2601.02980Jan 2026

View

Toward $\textit{Ab Initio}$ Quantum Simulations of Atomic Nuclei Using Noisy Qubits

2601.00315Jan 2026

View

Dissipative corrections to the particle momentum spectrum of a decoupling fluid

We present an \emph{ab initio} calculation within quantum statistical field theory and linear response theory, of the dissipative correction to the momentum spectrum of scalar particles emitted at decoupling (freeze-out) from a relativistic fluid assuming the initial state to be in local thermodynamic equilibrium. We obtain an expansion of the Wigner function of the interacting quantum field in terms of the gradients of the classical thermo-hydrodynamic fields - four-temperature vector and reduced chemical potential - evaluated on the initial local-equilibrium hypersurface, rather than on the decoupling (freeze-out) hypersurface as usual in kinetic theory. The gradient expansion includes an unexpected zeroth order term depending on the differences between thermo-hydrodynamic fields at the decoupling and the initial hypersurface. This term encodes a memory of the initial state which is related to the long-distance persistence of the correlation function between Wigner operator and stress-energy tensor and charged current that is discussed in detail. We address the phenomenological implications of these corrections for the momentum spectra measured in relativistic nuclear collisions.

2512.24994Dec 2025

View

Non-Equilibrium Dynamics in QCD and Holography

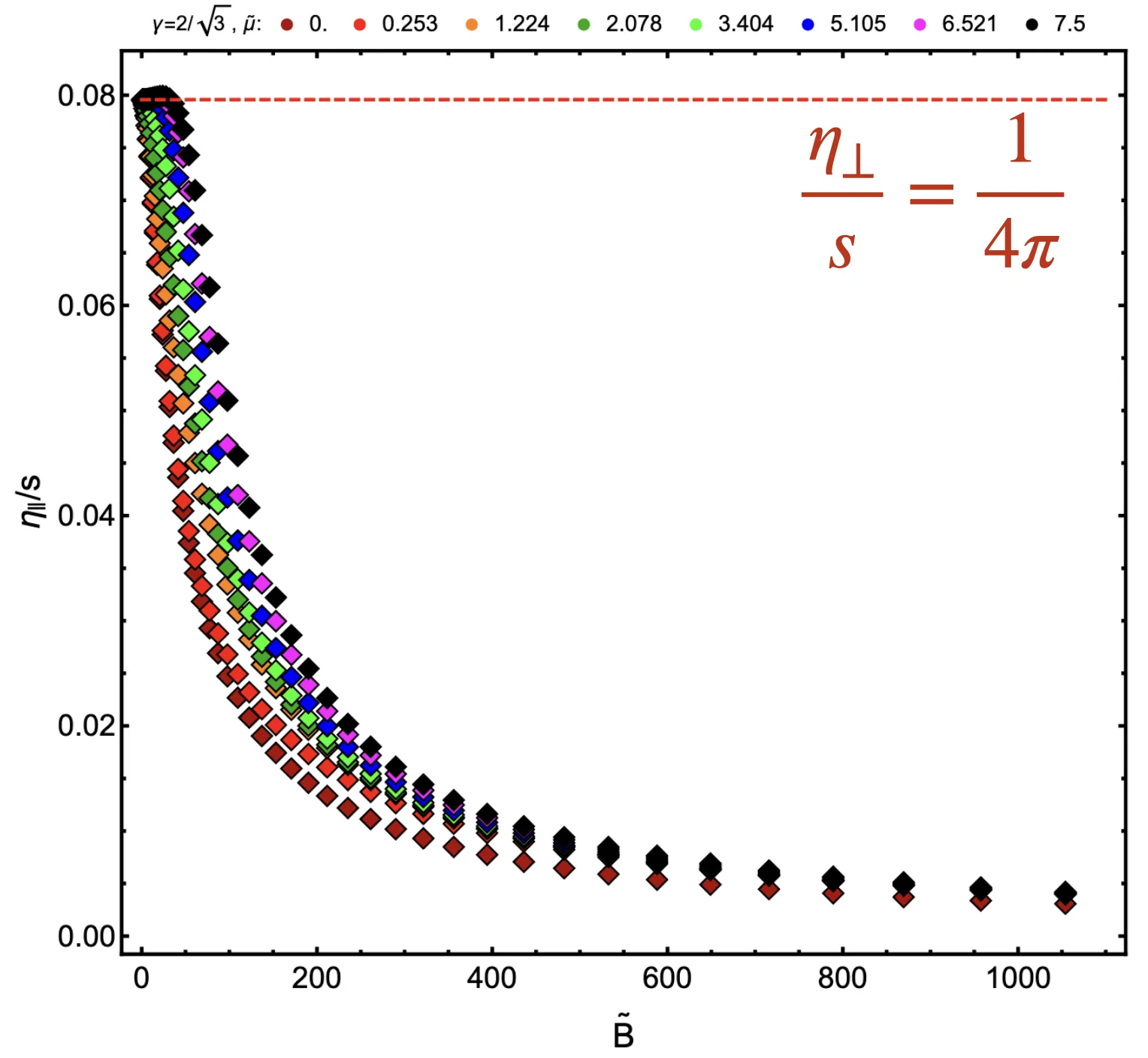
The plasma generated in heavy ion collisions goes through different phases in its time evolution. While early times right after the collision are governed by far-from equilibrium dynamics, later times are believed to be well described by near-equilibrium dynamics. While the regimes of non-equilibrium are prohibitively complicated to describe within QCD, effective descriptions such as hydrodynamics provide a viable approach. In addition, holographic descriptions allow access to the full non-equilibrium dynamics at strong coupling. In this presentation, we review three examples of such hydrodynamic approaches and corresponding holographic descriptions: 1) non-equilibrium shear viscosity, 2) propagation of non-equilibrium sound waves, and 3) the non-equilibrium chiral magnetic effect.

2512.24909Dec 2025

View

2512.23456

Poles from the conserved kinetic equation : The emerging gradient structure and causality riddle of relativistic hydrodynamics

In this work, the poles and the resulting dispersion spectra from the relativistic kinetic equation have been analyzed with the help of a proposed collision kernel that conserves both the energy-momentum tensor and particle current by construction. The dispersion relations, which originally come out in the form of logarithmic divergences, in the long wavelength limit exhibit the systematic gradient structure of the relativistic hydrodynamics. The key result is that, in the derivative expansion series, the spatial gradients appear in perfect unison with the temporal gradients in the non-local relaxation operator like forms. It is then shown that this dispersion structure, including non-local temporal derivatives, is essential for the preservation of causality of the theory truncated at any desired order.

2512.23456Dec 2025

View

Neutron Star Equation of State with Nucleon Short-Range Correlations: A Concise Review and Open Issues

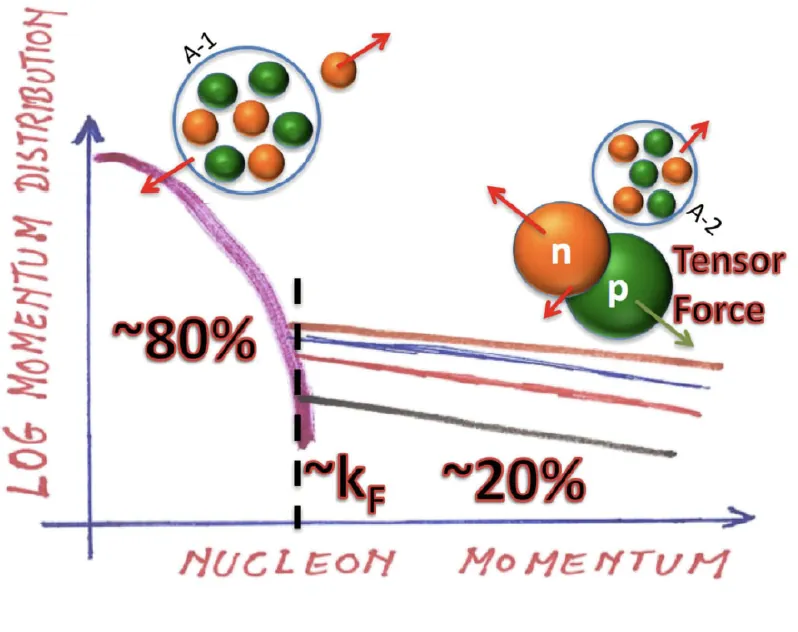
Nucleon short-range correlations (SRCs) and the associated high-momentum tail (HMT) in its momentum distribution $n(k)$ represent a universal feature of strongly interacting Fermi systems. In nuclear matter, SRCs arise primarily from the spin-isospin dependence of the tensor and short-range components of the nucleon-nucleon interaction, leading to a substantial depletion of its Fermi sea and a characteristic $k^{-4}$ tail populated predominantly by isosinglet neutron-proton pairs. These microscopic structures modify both the kinetic and interaction contributions to the Equation of State (EOS) of dense matter and thereby influence a broad range of neutron-star (NS) properties. This short review provides a streamlined overview of how SRC-induced changes in $n(k)$ reshape the kinetic EOS, including its symmetry energy part and how these effects propagate into macroscopic NS observables, including mass-radius relations, tidal deformabilities, direct Urca thresholds and core-crust transition. We summarize key existing results, highlight current observational constraints relevant for testing SRC-HMT effects, and outline open questions for future theoretical, experimental, and multimessenger studies of dense nucleonic matter.

2512.23455Dec 2025

View

Dissociation driven quarkonium spin alignment in Pb--Pb collisions at $\sqrt{s_{\rm NN}} = 5.02$ TeV

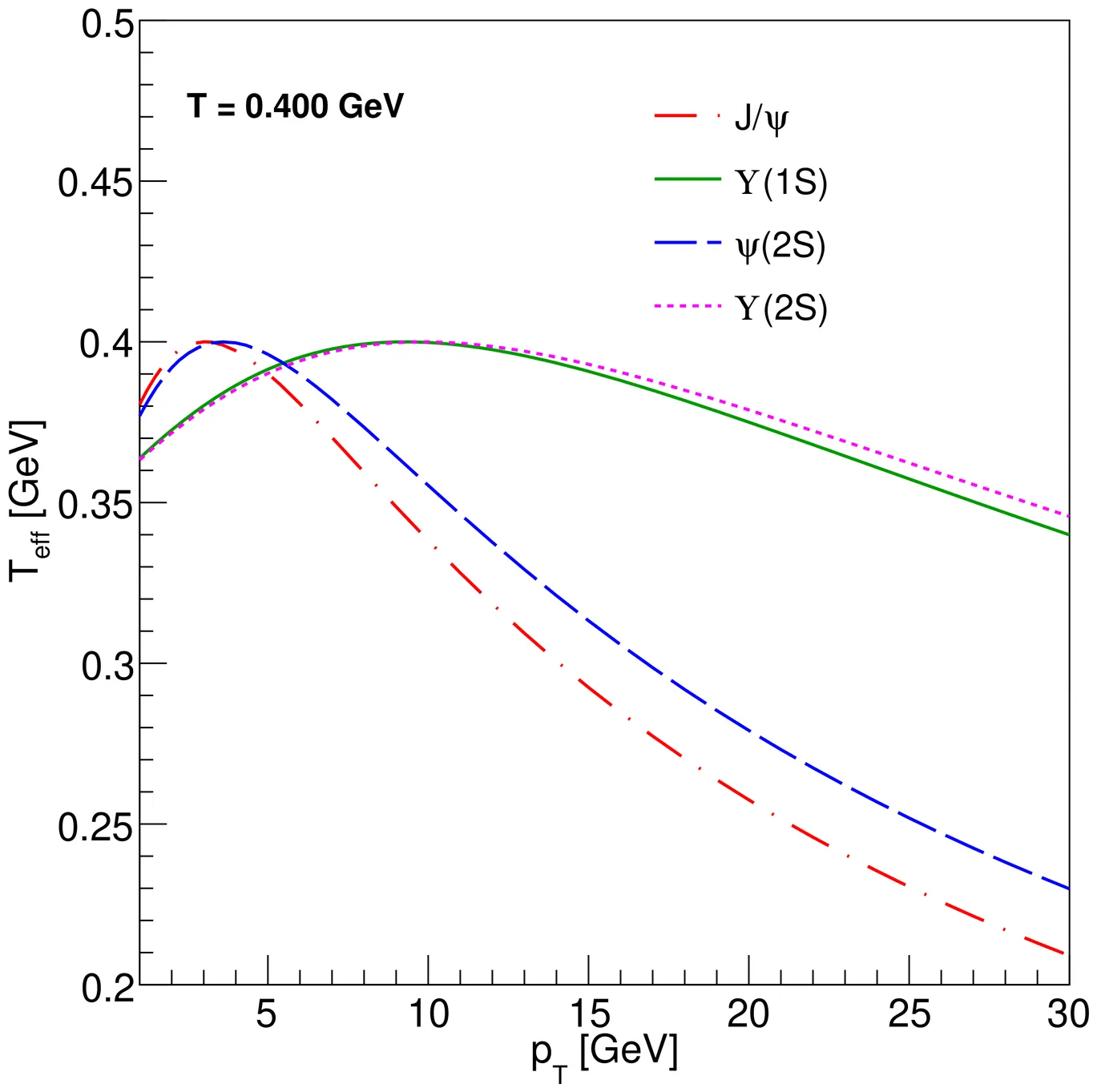
The observation of spin alignment of quarkonia in ultra-relativistic heavy-ion collisions provides deep insight into the possible formation of the quark-gluon plasma (QGP). The present study investigates the spin alignment of quarkonia induced by dissociation mechanisms arising from medium effects imposed on quarkonia. We implement an effective Hamiltonian with a medium-modified color-singlet potential to incorporate the coupling of quarkonium spin with medium vorticity. This coupling gives rise to spin-dependent dissociation, which we identify as a plausible mechanism contributing to quarkonium spin alignment. Within the ambit of second-order relativistic viscous hydrodynamics, we calculate the spin-dependent decay widths of charmonium ($J/ψ$, $ψ$(2S)) and bottomonium ($Υ$(1S), $Υ$(2S)) in a rotating thermal medium, including collisional damping and gluonic dissociation effects. We evaluate the observable $ρ_{00}$ for Pb--Pb collisions at $\sqrt{s_{\rm NN}} = 5.02$ TeV as a function of transverse momentum of the quarkonia, charged particle multiplicity, and medium rotation. The results demonstrate that medium vorticity modifies the quarkonia net decay width and, as a consequence, quarkonia spin alignment gets modified. These findings suggest new directions for understanding spin transport and the microscopic dynamics of vortical QGP.

2512.18728Dec 2025

View

Relativistic superfluid profiles near critical surfaces

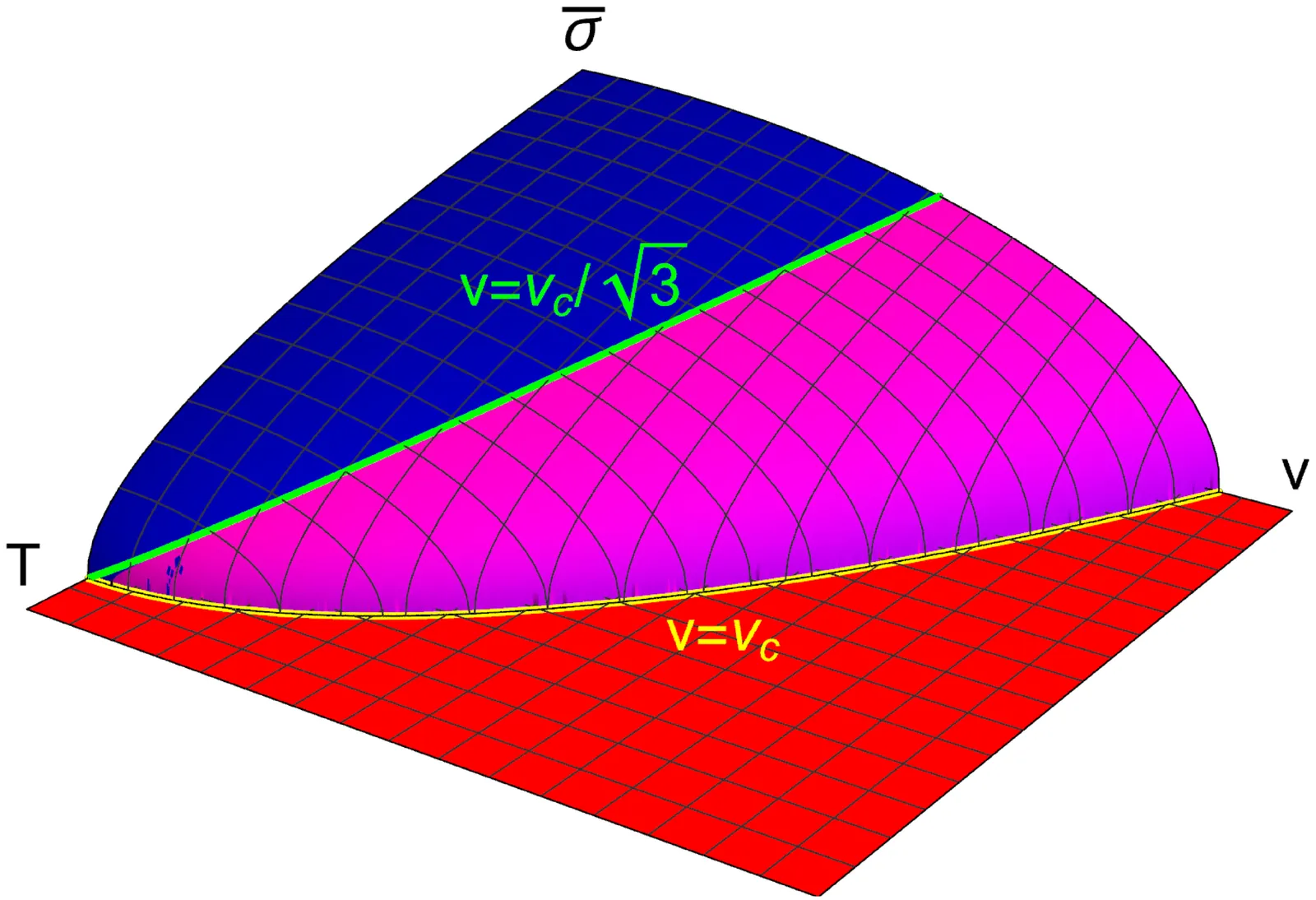
Landau's two-fluid model of superfluidity ceases to apply in regions where the condensate amplitude exhibits rapid spatial variation, such as vortex cores or in the vicinity of container walls. A recently proposed relativistic Gross-Pitaevskii-type framework treats the condensate as an independent scalar degree of freedom, enabling a controlled analysis of such regimes. We use it to construct stationary superflows close to the superfluid-normal phase boundary, and examine their stability. We obtain an exact expression for Landau's critical velocity and show that the standard Newtonian profiles (such as the near-vortex condensate depletion or the boundary-layer decay) persist unmodified in the relativistic setting. We further analyse a genuinely relativistic configuration in which an accelerated superfluid develops a phase boundary induced by Tolman temperature gradients.

2512.16797Dec 2025

View

Entangled two-proton emission from 16Ne and its sensitivity to diproton correlation

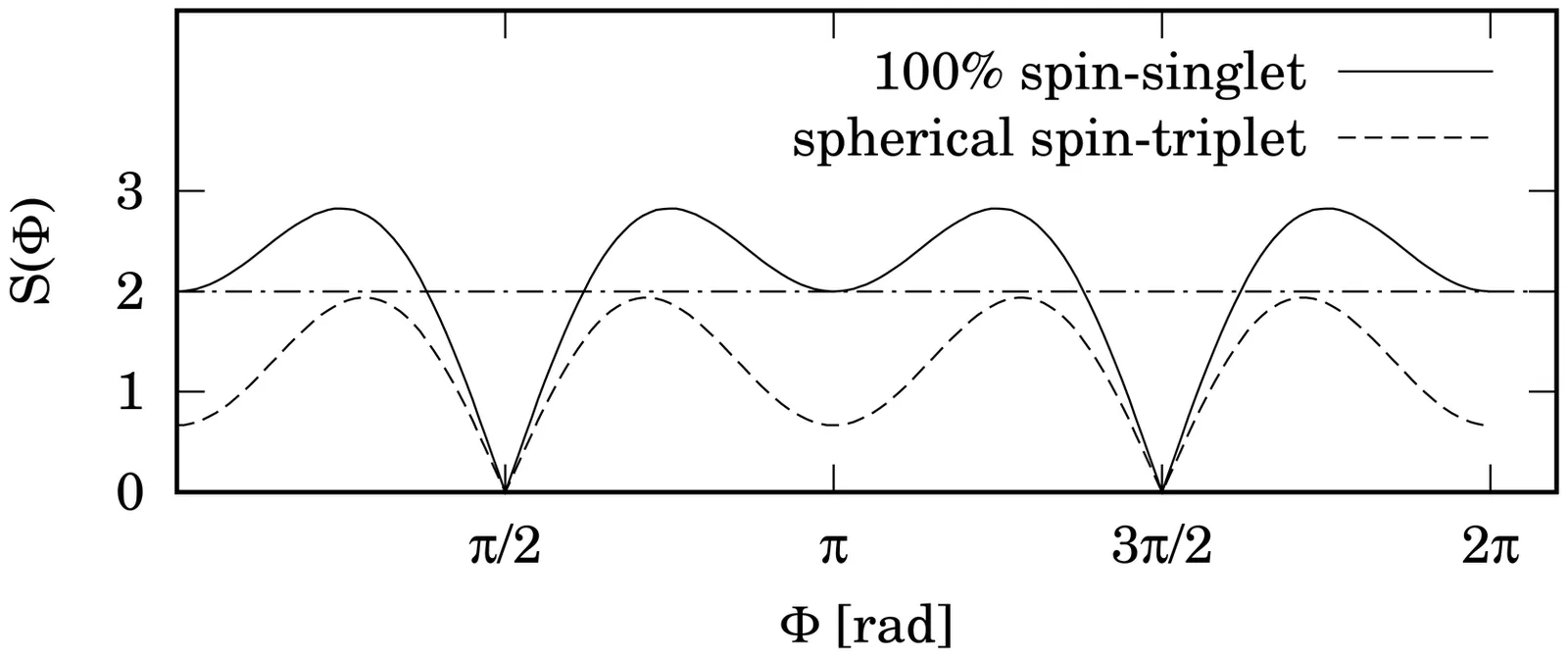
We discuss how the spin correlation, which reflects the quantum entanglement between two fermions, can serve as a probe of diproton correlation in the two-proton ($2p$) emission. We investigated the 16Ne nucleus using the time-dependent three-body (14O + 2p) model, and found that the $2p$-spin correlation exceeded the limit of local-hidden-variable (LHV) theory when the initial state had a spin-singlet diproton configuration. In contrast, for other configurations, it was remarkably reduced. This suggests that a strong initial diproton correlation is essential to generate a spin correlation nearly identical to that of a pure spin-singlet diproton. Such sensitivity indicates that $2p$-spin correlation can serve as a sensitive probe of diproton configurations, which could facilitate future studies on quantum entanglement and spin-dependent phenomena in atomic nuclei as well as in broader multi-fermion systems.

2512.15879Dec 2025

View

Leptophilic Interactions in Nuclear Energy Density Functional Theory

2512.11770Dec 2025

View

Finite-range pairing in nuclear density functional theory

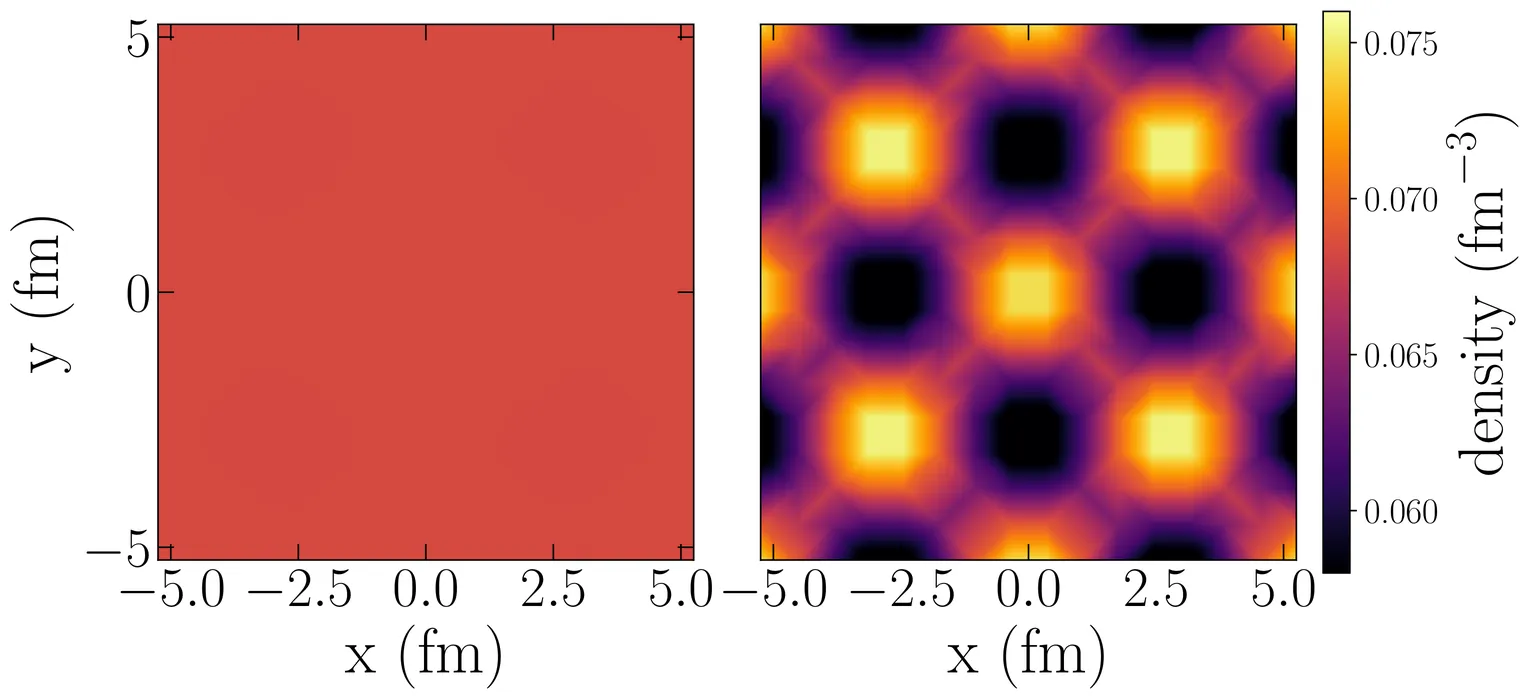
Pairing correlations are ubiquitous in low-energy states of atomic nuclei. To incorporate them within nuclear density functional theory, often used for global computations of nuclear properties, pairing functionals that generate nucleonic pair densities and pairing fields are introduced. Many pairing functionals currently used can be traced back to zero-range nucleon-nucleon interactions. Unfortunately, such functionals are plagued by deficiencies that become apparent in large model spaces that contain unbound single-particle (continuum) states. In particular, the underlying computational schemes diverge as the single-particle space increases, and the results depend on how marginally occupied states are incorporated. These problems become more pronounced for pairing functionals that contain gradient-density dependence, such as in the Fayans functional. To remedy this, finite-range pairing functionals are introduced. In this study, this is done by folding the pair density with Gaussians. We show that a folding radius of about 1\,fm offers the best compromise between quality and stability, and substantially reduces the pathological behavior in different numerical applications.

2511.08366Nov 2025

View

$α$-decay half-lives and $α$-cluster preformation factors of nuclei around $N=Z$ line

In this work, a microscopic effective nucleon-nucleon interaction based on the Dirac-Brueckner-Hartree-Fock $G$ matrix starting from a bare nucleon-nucleon interaction is used to explore the $α$-decay half-lives of the nuclei near $N=Z$ line. Specifically, the $α$-nucleus potential is constructed by doubly folding the effective nucleon-nucleon interaction with respect to the density distributions of both the $α$-cluster and daughter nucleus. Moreover, the $α$-cluster preformation factor is extracted by a cluster formation model. It is shown that the calculated half-lives can reproduce the experimental data well. Then, the $α$-decay half-lives that are experimentally unavailable for the nuclei around $N=Z$ are predicted, which are helpful for searching for the new candidates of $α$-decay in future experiments. In addition, by analyzing the proton-neutron correlation energy and two protons-two neutrons correlation energy of $Z=52$ and $Z=54$ isotopes, the $α$-cluster preformation factor evolution with $N$ is explained. Furthermore, it is found that the two protons-two neutrons interaction plays more important role in $α$-cluster preformation than the proton-neutron interaction. Meanwhile, proton-neutron interaction results in the odd-even effect of the $α$-cluster preformation factor.

2511.08051Nov 2025

View

What happens in hydrodynamic simulations of heavy-ion collisions when causality is violated?

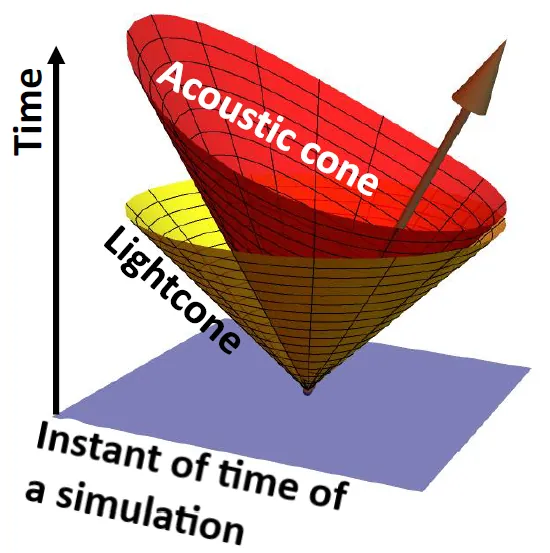
We summarize our recent investigations on how causality violations in Israel-Stewart-type relativistic viscous hydrodynamic simulations can give rise to both analytical and numerical instabilities. The classification of spacetime regions into causal and stable ("good"), acausal but stable ("bad"), and acausal and unstable ("ugly") is reviewed. We compare the predictions of the MUSIC hydrodynamic solver with an analytical solution, and demonstrate how the acausality-driven instabilities develop in a simple one-dimensional scenario.

2511.07946Nov 2025

View

Renormalization-Group Invariant Parity-Doublet Model for Nuclear and Neutron-Star Matter

The Parity-Doublet Model (PDM) is a chirally invariant effective theory for strong-interaction matter involving nucleons and their opposite-parity partners in a parity-doubling framework. We introduce a multiplicatively renormalizable mean-field approach to include the baryonic vacuum contributions to the resulting grand-canonical potential in an explicitly renormalization-group invariant form. As an application, we evaluate the pertinent thermodynamics of two-flavor symmetric and asymmetric nuclear matter, focusing on the restoration of spontaneously broken chiral symmetry at baryon densities and temperatures relevant for the astrophysics of neutron stars. Special attention is paid to the effect of the baryonic vacuum fluctuations on the evolution of chiral condensate with baryon density and temperature for specific choices of the chirally invariant baryon mass $m_0$ to demonstrate the importance of consistently including these vacuum fluctuations in the PDM.

2511.07226Nov 2025

View

Jacobi Coordinates on Hyper-tori and Geometric Factors in the Volume Dependencies

We derive the volume dependence of bound states from a cluster-cluster picture with nucleon degrees of freedom. To achieve this, we demonstrate how to construct Jacobi coordinates on the lattice under the periodic boundary. A constant factor called ``Geometric factor'' appears in the generalization from point-like particles to clusters. We validate our derivation using many-body calculations, specifically, we find this factor to be essential in extracting asymptotic normalization constants from lattice calculations of \isotope[16]{O} ground state.

2511.06726Nov 2025

View

Analysis of elastic $α$-$^{12}$C scattering with machine learning in the cluster effective field theory

We analyze the elastic $α$-$^{12}$C scattering including the contribution of resonance states below the $p$-$^{15}$N breakup threshold energy. We use the cluster effective field theory in which scattering amplitude is expanded in terms of the effective range expansion parameters for the angular momentum states from $l=0$ to $l=6$. The amplitude contains 37 parameters, which are determined by fitting to 11,392 differential cross section data points of the elastic $α$-$^{12}$C scattering. To optimize the fitting process, we implement the Differential Evolution (DE) algorithm, which performs a global search over the high-dimensional parameter space and consistently converges to the same minimum $χ^{2}$ value across independent runs, suggesting proximity to the global minimum within the explored domain. In parallel, the Markov chain Monte Carlo method is used to cross-check the DE results and to estimate the parameter uncertainties. The best fit yields $χ^{2}/N\!\simeq\!6.2$ for the elastic scattering data. Using the determined 37 parameters, we calculate the differential cross sections and the phase shifts of the elastic $α$-$^{12}$C scattering and compare the results with experimental data and those of an $R$-matrix analysis. Our result of the cross section agrees with the experimental data as accurately as an $R$-matrix analysis. The results demonstrate that the cluster effective field theory, combined with machine learning based optimization and uncertainty quantification, provides a reliable and systematic framework for application to low-energy phenomena relevant to stellar evolution and nucleosynthesis.

2511.06382Nov 2025

View

Universal modified function in conjunction with the short range correlation effect to extract the nuclear $xF_3^A$ structure function

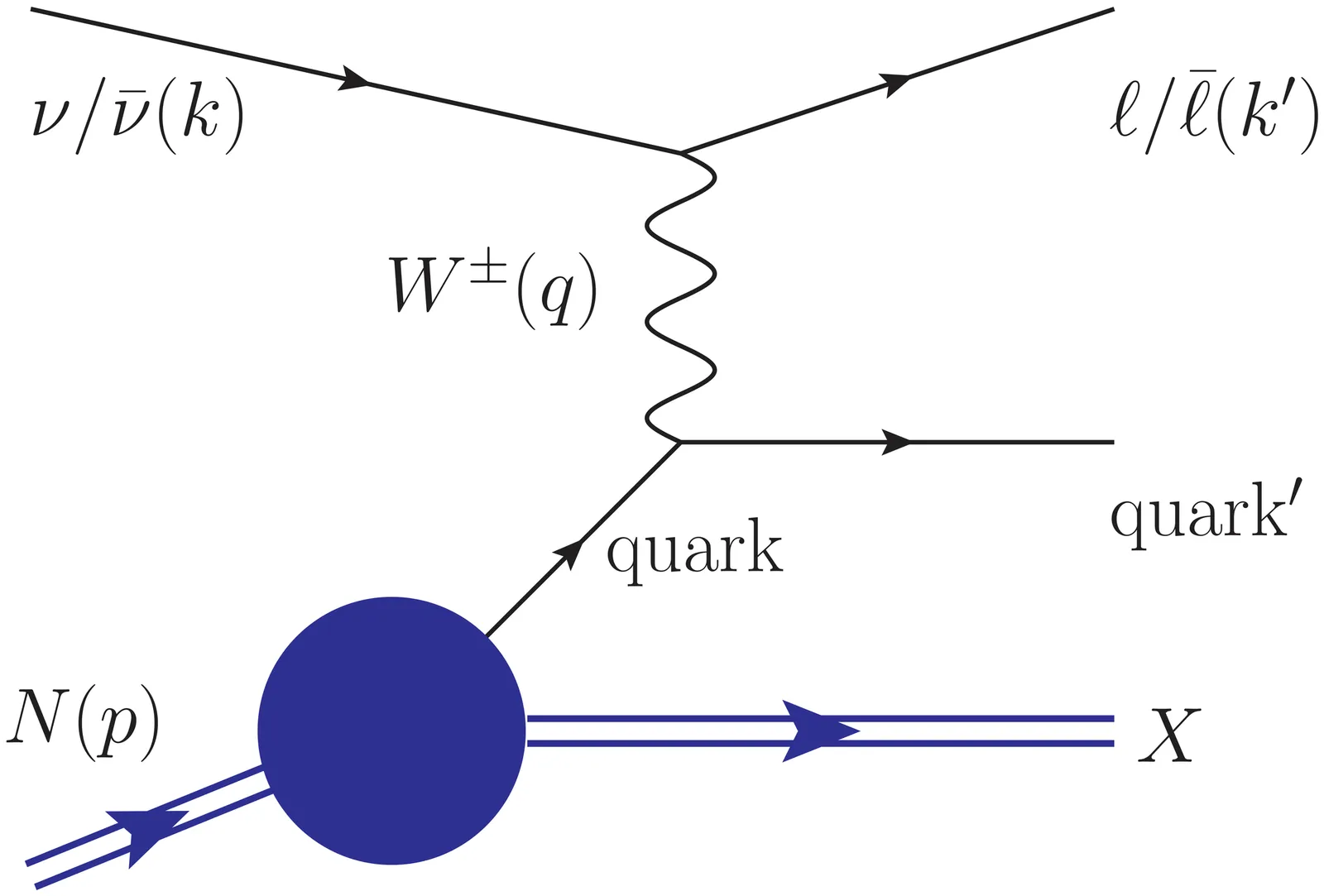
Parton distribution functions (PDFs) are comprehensive and not reliant on the process. They are affected by nuclear matter during nuclear scattering process. As a recent approach, in order to study the nuclear PDFs (nPDFs), the nucleon pair PDFs are utilized to describe parton distributions in the nucleon pair which are confined to a nucleus. Nucleon pair PDFs stem from nucleon-nucleon correlation which is called short range correlation (SRC) and are proportional to common nucleon PDFs. In this regard a modified universal function is constructed which provides a test for SRC in (neutrino)-nucleus scattering. In fact we can show that the modification of the structure function of nucleons bound in atomic nuclei (known as the EMC effect) are consistently accounted for within the frame work of a universal modification of nucleons in SRC pairs. In this article, based on the strategy which was introduced in Ref.\cite{nature}, we are investigating to find the universality behaviour for the ratio of nonsinglet $xF_3^A$ nuclear structure function. The numerical calculations performed within the CTEQ framework confirm the universality feature of the concerned ratio, as has been established for the ratio of the structure function $F^A_2$ in Ref. \cite{nature}. Following that we reformulate the $R_{EMC}$ nuclear weight function which relates the free and bound structure function in terms of modified universal function. It makes us a possibility to achieve $R_{EMC}$ and finally $xF_3^A$ nuclear structure function for each nucleus only by considering the specified feature of nucleus.The results are compared with the nuclear $xF_3$ structure function which are computing from bound PDFs, based on some parameterizations models. The findings, considering the SRC effect, demonstrating qualitative agreement with nCTEQ15 and EPPS21 parametrization models and also the available experimental data.

2511.06099Nov 2025

View

Microscopic study of low-lying states in odd-mass nuclei for atomic electric dipole moment searches

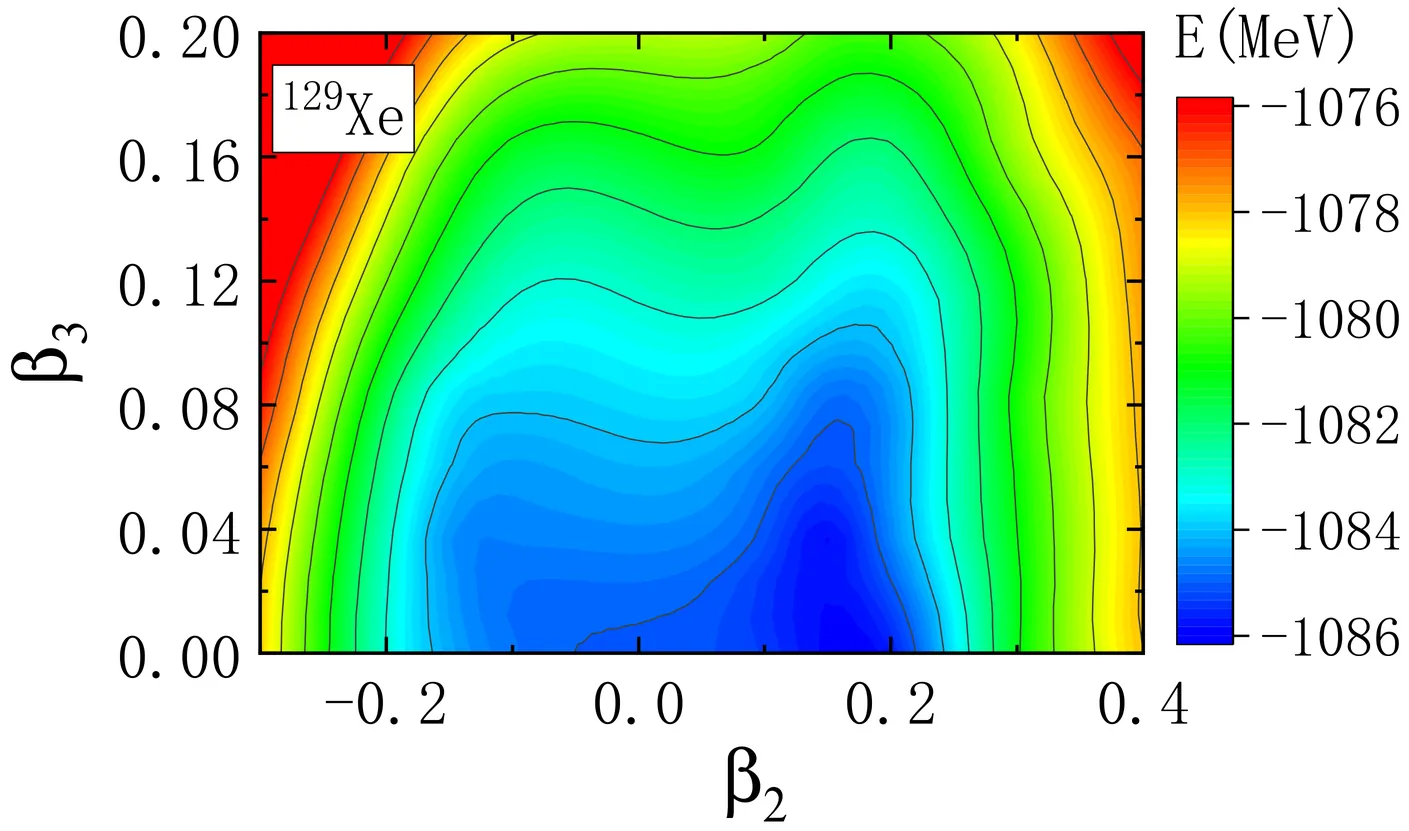
We present a microscopic study of the low-lying states of five odd-mass nuclei of particular interest for experimental searches of atomic electric dipole moments (EDMs): $^{129}$Xe, $^{199}$Hg, $^{225}$Ra, $^{229}$Th, and $^{229}$Pa. The analysis is performed within the recently developed multi-reference covariant density functional theory (MR-CDFT), which incorporates symmetry restoration and configuration mixing based on self-consistent mean-field solutions. The calculated energy spectra and electromagnetic observables of these nuclei are reasonably well reproduced without introducing any parameters beyond those of the underlying universal relativistic energy density functional. The results demonstrate the reliability of MR-CDFT in describing the structure of these nuclei and in providing essential input on nuclear Schiff moments relevant to ongoing EDM searches.

2511.05984Nov 2025

View

Search for shape-isomers in the Pt-Hg-Pb region

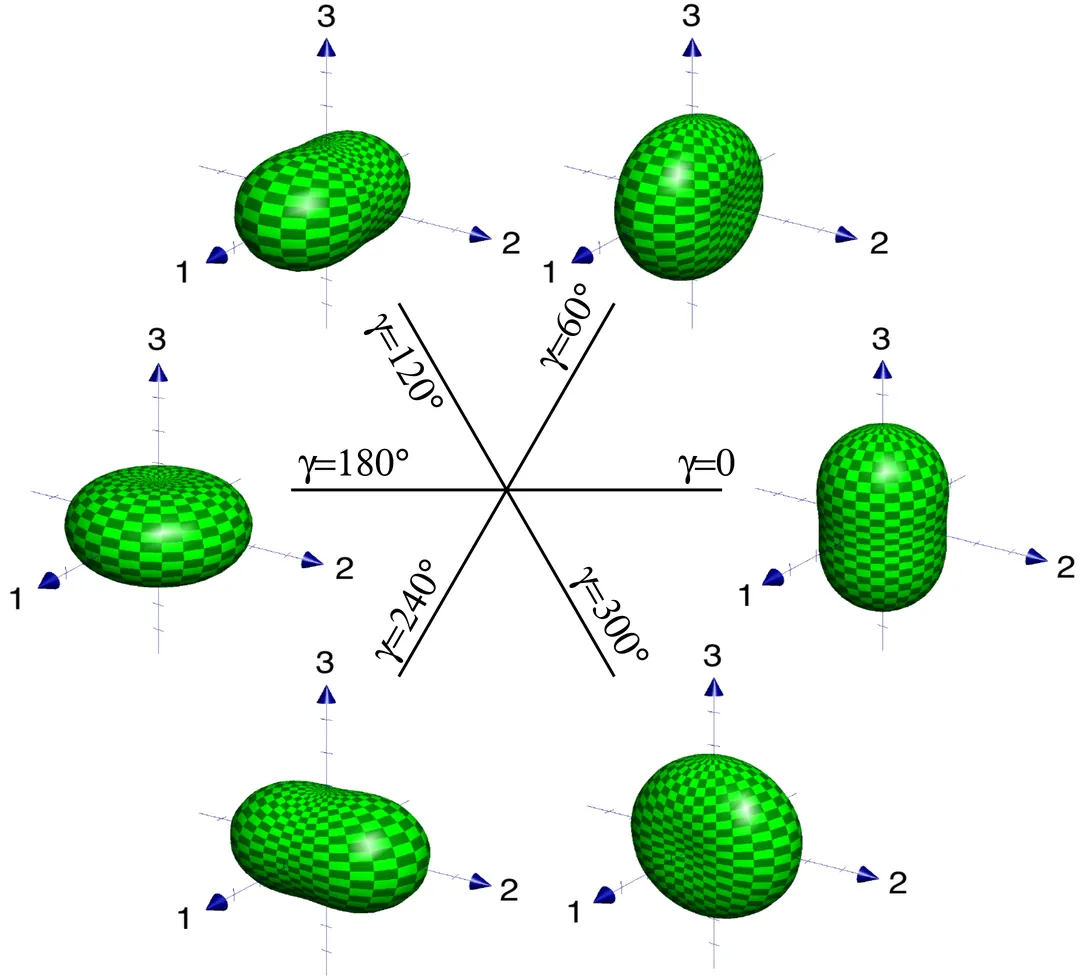
Potential energy surfaces of nine even-even isotopes of Pt, Hg, and Pb around $^{186}$Pt are evaluated within a macroscopic-microscopic model based on the Lublin-Strasbourg-Drop macroscopic energy and the microscopic energy obtained using the Yukawa-folded mean-field potential to establish the Strutinski shell corrections and the pairing correlation energy through the BCS approach with a monopole pairing force. The rapidly converging Fourier-over-Spheroid shape parametrization is used to describe nuclear deformations. The stability of the identified shape isomeric states with respect to non-axial and higher-order deformations is investigated. It is also found that in the description of non-axial deformations special attention needs to be devoted to the orientation of the triaxial shape. For the example of the $^{186}$Hg nucleus, where three prolate shape-isomeric states are found, it is shown that the potential energy surface obtained in our model is close to the one obtained in the Hartree-Fock-Bogoliubov theory with the Gogny energy-density functional.

2511.05918Nov 2025

View

The size of the quark-gluon plasma in ultracentral collisions: impact of initial density fluctuations on the average transverse momentum

Recent experiments have shown that the mean transverse momentum $\langle p_T\rangle$ of outgoing particles increases as a function of the particle multiplicity in ultracentral nucleus-nucleus collisions at collider energies. This increase was originally predicted on the basis of simulations where the multiplicity increase occurred at constant volume, so that it implied a larger density and temperature. However, recent state-of-the-art simulations have shown that, for some models of initial condition, the volume may vary with the multiplicity in ultracentral collisions. We elucidate this effect by analytically relating the variation of the volume to the radial distribution of the one- and two-point functions of the fluctuating density field. We show that the volume variation is small if the total entropy of the ultracentral collisions scales with the mass number of the colliding isotopes. We argue that probing detailed transverse distributions of initial-state fluctuations through the ultracentral $\langle p_T\rangle$ has nontrivial implications for models of nuclear structure and of the pre-equilibrium stages.

2511.04605Nov 2025

View

Page 1 of 20