Trending in Statistics
Enhanced Diffusion Sampling: Efficient Rare Event Sampling and Free Energy Calculation with Diffusion Models
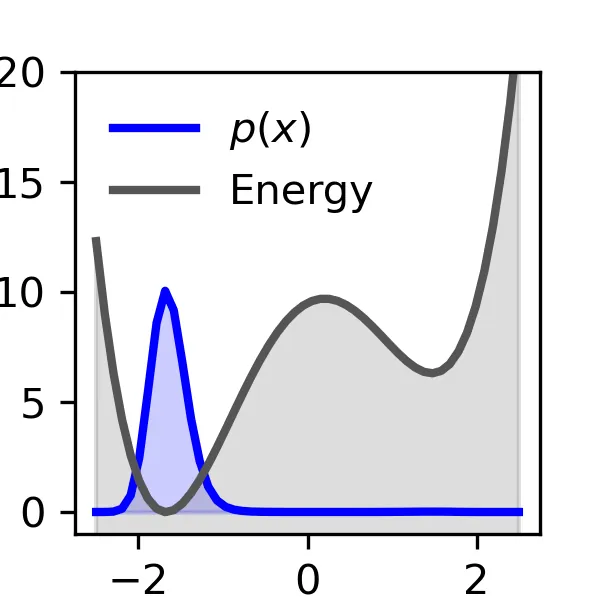
The rare-event sampling problem has long been the central limiting factor in molecular dynamics (MD), especially in biomolecular simulation. Recently, diffusion models such as BioEmu have emerged as powerful equilibrium samplers that generate independent samples from complex molecular distributions, eliminating the cost of sampling rare transition events. However, a sampling problem remains when computing observables that rely on states which are rare in equilibrium, for example folding free energies. Here, we introduce enhanced diffusion sampling, enabling efficient exploration of rare-event regions while preserving unbiased thermodynamic estimators. The key idea is to perform quantitatively accurate steering protocols to generate biased ensembles and subsequently recover equilibrium statistics via exact reweighting. We instantiate our framework in three algorithms: UmbrellaDiff (umbrella sampling with diffusion models), $Δ$G-Diff (free-energy differences via tilted ensembles), and MetaDiff (a batchwise analogue for metadynamics). Across toy systems, protein folding landscapes and folding free energies, our methods achieve fast, accurate, and scalable estimation of equilibrium properties within GPU-minutes to hours per system -- closing the rare-event sampling gap that remained after the advent of diffusion-model equilibrium samplers.
2602.16634
Feb 2026Statistical Learning
Error Propagation and Model Collapse in Diffusion Models: A Theoretical Study
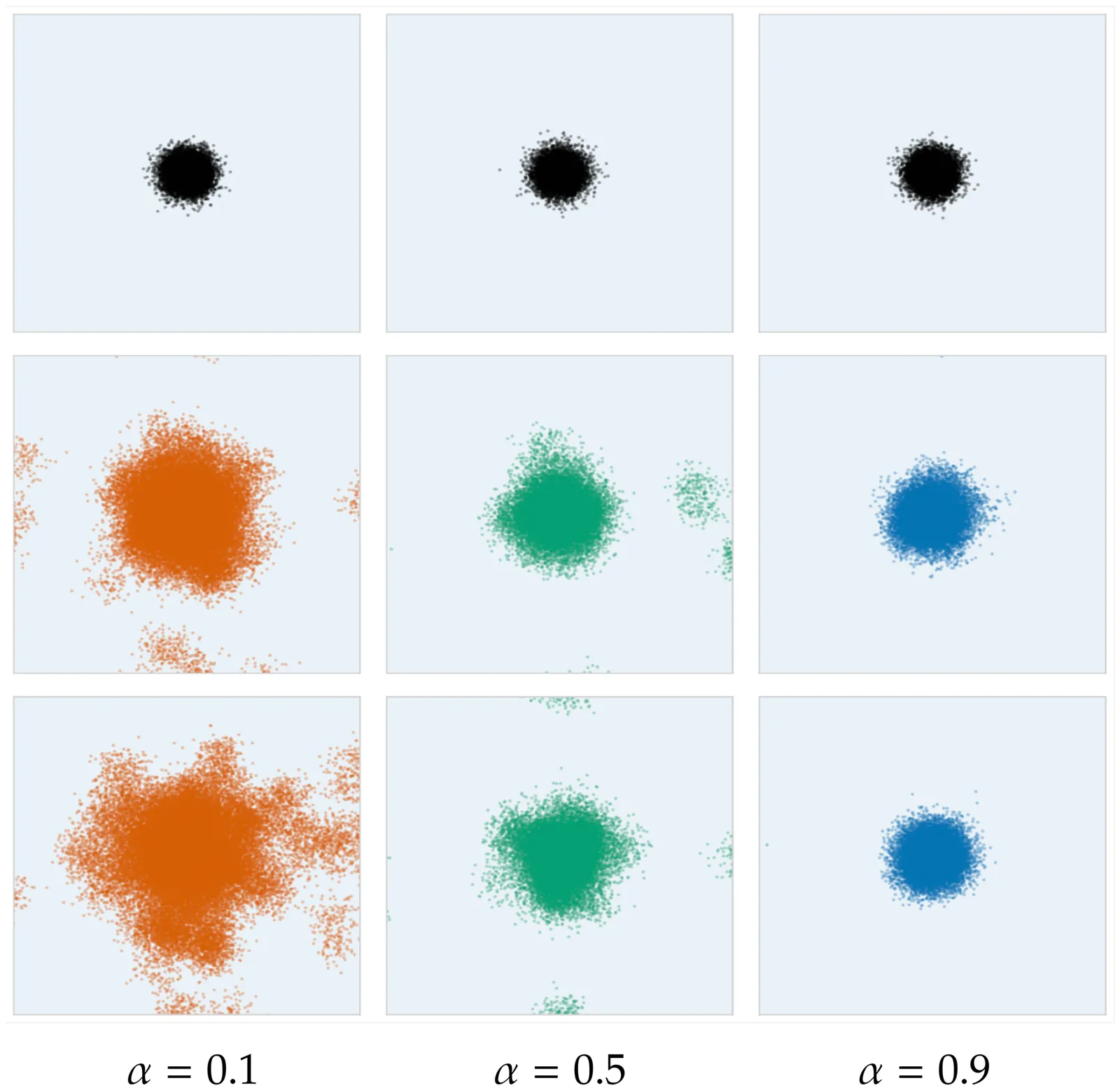
Machine learning models are increasingly trained or fine-tuned on synthetic data. Recursively training on such data has been observed to significantly degrade performance in a wide range of tasks, often characterized by a progressive drift away from the target distribution. In this work, we theoretically analyze this phenomenon in the setting of score-based diffusion models. For a realistic pipeline where each training round uses a combination of synthetic data and fresh samples from the target distribution, we obtain upper and lower bounds on the accumulated divergence between the generated and target distributions. This allows us to characterize different regimes of drift, depending on the score estimation error and the proportion of fresh data used in each generation. We also provide empirical results on synthetic data and images to illustrate the theory.
2602.16601
Feb 2026Statistical Learning

Functional Central Limit Theorem for Stochastic Gradient Descent
We study the asymptotic shape of the trajectory of the stochastic gradient descent algorithm applied to a convex objective function. Under mild regularity assumptions, we prove a functional central limit theorem for the properly rescaled trajectory. Our result characterizes the long-term fluctuations of the algorithm around the minimizer by providing a diffusion limit for the trajectory. In contrast with classical central limit theorems for the last iterate or Polyak-Ruppert averages, this functional result captures the temporal structure of the fluctuations and applies to non-smooth settings such as robust location estimation, including the geometric median.
2602.15538
Feb 2026Statistical Learning
Conjugate Learning Theory: Uncovering the Mechanisms of Trainability and Generalization in Deep Neural Networks
In this work, we propose a notion of practical learnability grounded in finite sample settings, and develop a conjugate learning theoretical framework based on convex conjugate duality to characterize this learnability property. Building on this foundation, we demonstrate that training deep neural networks (DNNs) with mini-batch stochastic gradient descent (SGD) achieves global optima of empirical risk by jointly controlling the extreme eigenvalues of a structure matrix and the gradient energy, and we establish a corresponding convergence theorem. We further elucidate the impact of batch size and model architecture (including depth, parameter count, sparsity, skip connections, and other characteristics) on non-convex optimization. Additionally, we derive a model-agnostic lower bound for the achievable empirical risk, theoretically demonstrating that data determines the fundamental limit of trainability. On the generalization front, we derive deterministic and probabilistic bounds on generalization error based on generalized conditional entropy measures. The former explicitly delineates the range of generalization error, while the latter characterizes the distribution of generalization error relative to the deterministic bounds under independent and identically distributed (i.i.d.) sampling conditions. Furthermore, these bounds explicitly quantify the influence of three key factors: (i) information loss induced by irreversibility in the model, (ii) the maximum attainable loss value, and (iii) the generalized conditional entropy of features with respect to labels. Moreover, they offer a unified theoretical lens for understanding the roles of regularization, irreversible transformations, and network depth in shaping the generalization behavior of deep neural networks. Extensive experiments validate all theoretical predictions, confirming the framework's correctness and consistency.
2602.16177
Feb 2026Statistical Learning
 2602.09457
2602.09457From Average Sensitivity to Small-Loss Regret Bounds under Random-Order Model
We study online learning in the random-order model, where the multiset of loss functions is chosen adversarially but revealed in a uniformly random order. Building on the batch-to-online conversion by Dong and Yoshida (2023), we show that if an offline algorithm admits a $(1+\varepsilon)$-approximation guarantee and the effect of $\varepsilon$ on its average sensitivity is characterized by a function $\varphi(\varepsilon)$, then an adaptive choice of $\varepsilon$ yields a small-loss regret bound of $\tilde O(\varphi^{\star}(\mathrm{OPT}_T))$, where $\varphi^{\star}$ is the concave conjugate of $\varphi$, $\mathrm{OPT}_T$ is the offline optimum over $T$ rounds, and $\tilde O$ hides polylogarithmic factors in $T$. Our method requires no regularity assumptions on loss functions, such as smoothness, and can be viewed as a generalization of the AdaGrad-style tuning applied to the approximation parameter $\varepsilon$. Our result recovers and strengthens the $(1+\varepsilon)$-approximate regret bounds of Dong and Yoshida (2023) and yields small-loss regret bounds for online $k$-means clustering, low-rank approximation, and regression. We further apply our framework to online submodular function minimization using $(1\pm\varepsilon)$-cut sparsifiers of submodular hypergraphs, obtaining a small-loss regret bound of $\tilde O(n^{3/4}(1 + \mathrm{OPT}_T^{3/4}))$, where $n$ is the ground-set size. Our approach sheds light on the power of sparsification and related techniques in establishing small-loss regret bounds in the random-order model.
2602.09457
Feb 2026Statistical Learning
Meta Flow Maps enable scalable reward alignment
Controlling generative models is computationally expensive. This is because optimal alignment with a reward function--whether via inference-time steering or fine-tuning--requires estimating the value function. This task demands access to the conditional posterior $p_{1|t}(x_1|x_t)$, the distribution of clean data $x_1$ consistent with an intermediate state $x_t$, a requirement that typically compels methods to resort to costly trajectory simulations. To address this bottleneck, we introduce Meta Flow Maps (MFMs), a framework extending consistency models and flow maps into the stochastic regime. MFMs are trained to perform stochastic one-step posterior sampling, generating arbitrarily many i.i.d. draws of clean data $x_1$ from any intermediate state. Crucially, these samples provide a differentiable reparametrization that unlocks efficient value function estimation. We leverage this capability to solve bottlenecks in both paradigms: enabling inference-time steering without inner rollouts, and facilitating unbiased, off-policy fine-tuning to general rewards. Empirically, our single-particle steered-MFM sampler outperforms a Best-of-1000 baseline on ImageNet across multiple rewards at a fraction of the compute.
2601.14430
Jan 2026Statistical Learning
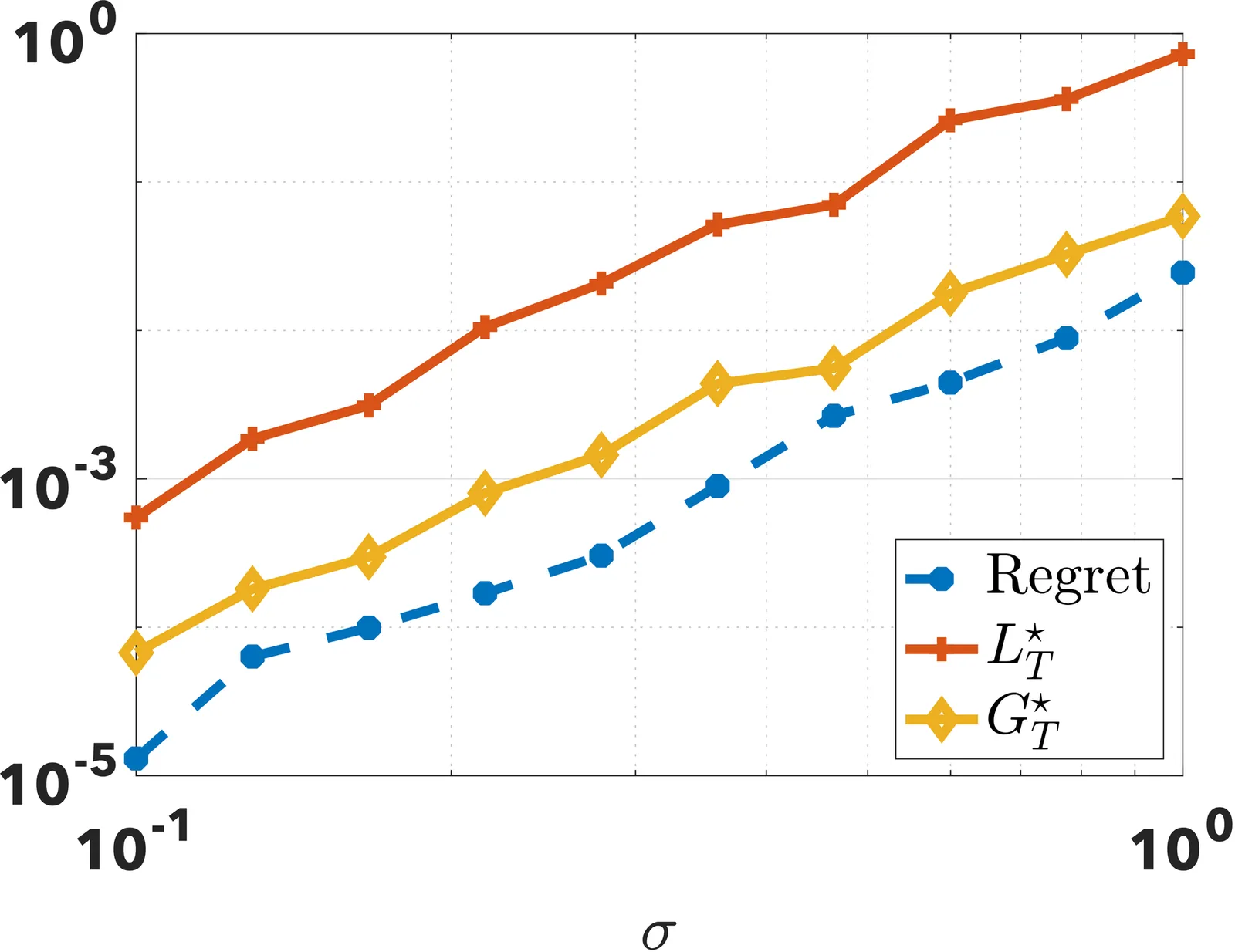
Small Gradient Norm Regret for Online Convex Optimization
This paper introduces a new problem-dependent regret measure for online convex optimization with smooth losses. The notion, which we call the $G^\star$ regret, depends on the cumulative squared gradient norm evaluated at the decision in hindsight $\sum_{t=1}^T \|\nabla \ell(x^\star)\|^2$. We show that the $G^\star$ regret strictly refines the existing $L^\star$ (small loss) regret, and that it can be arbitrarily sharper when the losses have vanishing curvature around the hindsight decision. We establish upper and lower bounds on the $G^\star$ regret and extend our results to dynamic regret and bandit settings. As a byproduct, we refine the existing convergence analysis of stochastic optimization algorithms in the interpolation regime. Some experiments validate our theoretical findings.
2601.13519
Jan 2026Statistical Learning
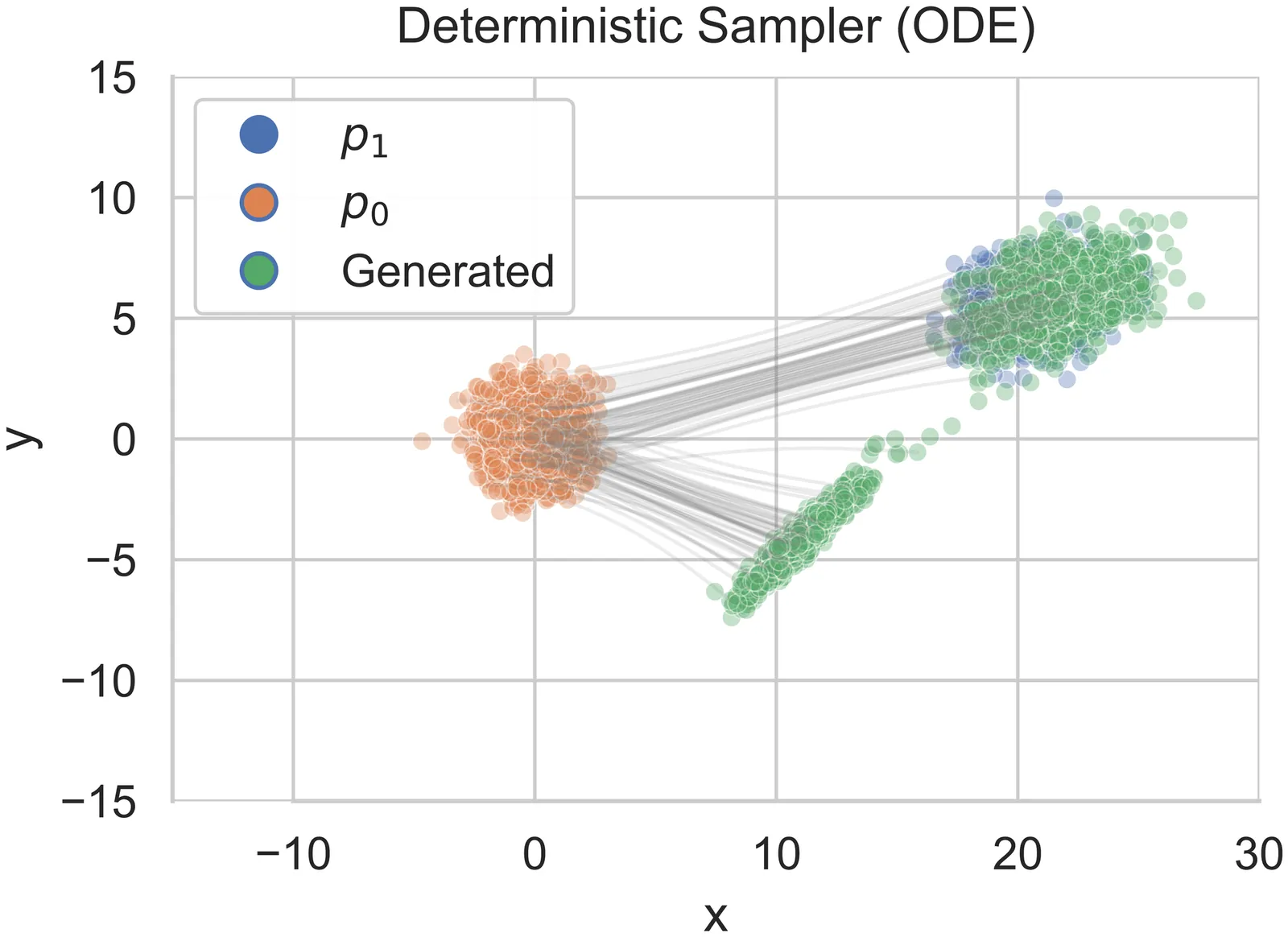
Low-Dimensional Adaptation of Rectified Flow: A New Perspective through the Lens of Diffusion and Stochastic Localization
In recent years, Rectified flow (RF) has gained considerable popularity largely due to its generation efficiency and state-of-the-art performance. In this paper, we investigate the degree to which RF automatically adapts to the intrinsic low dimensionality of the support of the target distribution to accelerate sampling. We show that, using a carefully designed choice of the time-discretization scheme and with sufficiently accurate drift estimates, the RF sampler enjoys an iteration complexity of order $O(k/\varepsilon)$ (up to log factors), where $\varepsilon$ is the precision in total variation distance and $k$ is the intrinsic dimension of the target distribution. In addition, we show that the denoising diffusion probabilistic model (DDPM) procedure is equivalent to a stochastic version of RF by establishing a novel connection between these processes and stochastic localization. Building on this connection, we further design a stochastic RF sampler that also adapts to the low-dimensionality of the target distribution under milder requirements on the accuracy of the drift estimates, and also with a specific time schedule. We illustrate with simulations on the synthetic data and text-to-image data experiments the improved performance of the proposed samplers implementing the newly designed time-discretization schedules.
2601.15500
Jan 2026Statistical Learning
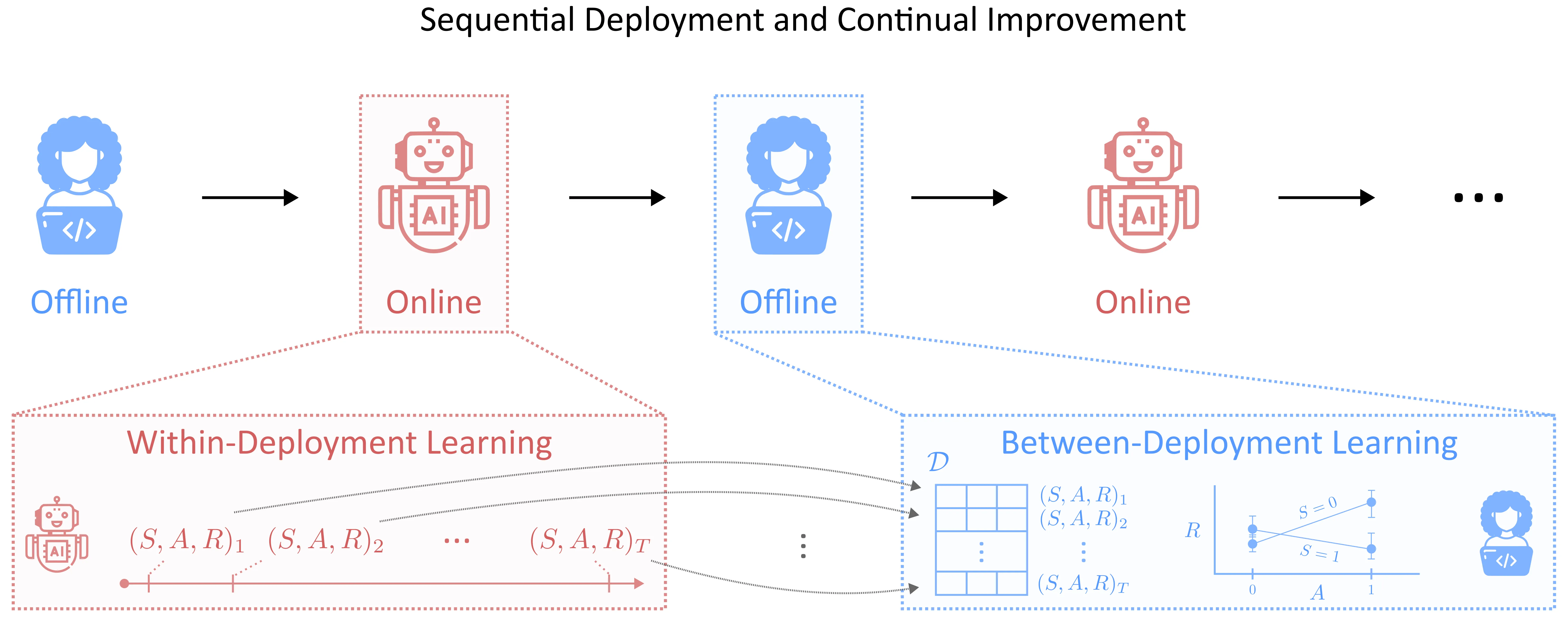
Statistical Reinforcement Learning in the Real World: A Survey of Challenges and Future Directions
Reinforcement learning (RL) has achieved remarkable success in real-world decision-making across diverse domains, including gaming, robotics, online advertising, public health, and natural language processing. Despite these advances, a substantial gap remains between RL research and its deployment in many practical settings. Two recurring challenges often underlie this gap. First, many settings offer limited opportunity for the agent to interact extensively with the target environment due to practical constraints. Second, many target environments often undergo substantial changes, requiring redesign and redeployment of RL systems (e.g., advancements in science and technology that change the landscape of healthcare delivery). Addressing these challenges and bridging the gap between basic research and application requires theory and methodology that directly inform the design, implementation, and continual improvement of RL systems in real-world settings. In this paper, we frame the application of RL in practice as a three-component process: (i) online learning and optimization during deployment, (ii) post- or between-deployment offline analyses, and (iii) repeated cycles of deployment and redeployment to continually improve the RL system. We provide a narrative review of recent advances in statistical RL that address these components, including methods for maximizing data utility for between-deployment inference, enhancing sample efficiency for online learning within-deployment, and designing sequences of deployments for continual improvement. We also outline future research directions in statistical RL that are use-inspired -- aiming for impactful application of RL in practice.
2601.15353
Jan 2026Applications
Efficient and Minimax-optimal In-context Nonparametric Regression with Transformers
We study in-context learning for nonparametric regression with $α$-Hölder smooth regression functions, for some $α>0$. We prove that, with $n$ in-context examples and $d$-dimensional regression covariates, a pretrained transformer with $Θ(\log n)$ parameters and $Ω\bigl(n^{2α/(2α+d)}\log^3 n\bigr)$ pretraining sequences can achieve the minimax-optimal rate of convergence $O\bigl(n^{-2α/(2α+d)}\bigr)$ in mean squared error. Our result requires substantially fewer transformer parameters and pretraining sequences than previous results in the literature. This is achieved by showing that transformers are able to approximate local polynomial estimators efficiently by implementing a kernel-weighted polynomial basis and then running gradient descent.
2601.15014
Jan 2026Statistical Learning
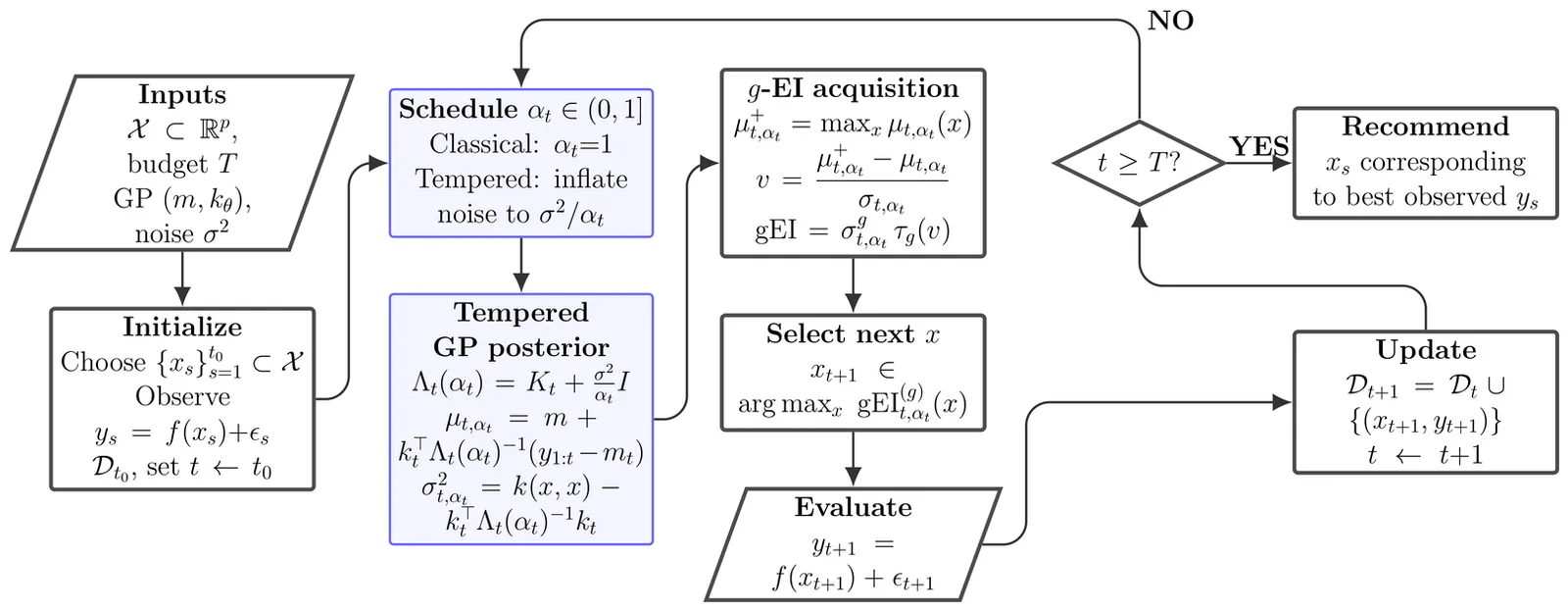
Robust Bayesian Optimization via Tempered Posteriors
Bayesian optimization (BO) iteratively fits a Gaussian process (GP) surrogate to accumulated evaluations and selects new queries via an acquisition function such as expected improvement (EI). In practice, BO often concentrates evaluations near the current incumbent, causing the surrogate to become overconfident and to understate predictive uncertainty in the region guiding subsequent decisions. We develop a robust GP-based BO via tempered posterior updates, which downweight the likelihood by a power $α\in (0,1]$ to mitigate overconfidence under local misspecification. We establish cumulative regret bounds for tempered BO under a family of generalized improvement rules, including EI, and show that tempering yields strictly sharper worst-case regret guarantees than the standard posterior $(α=1)$, with the most favorable guarantees occurring near the classical EI choice. Motivated by our theoretic findings, we propose a prequential procedure for selecting $α$ online: it decreases $α$ when realized prediction errors exceed model-implied uncertainty and returns $α$ toward one as calibration improves. Empirical results demonstrate that tempering provides a practical yet theoretically grounded tool for stabilizing BO surrogates under localized sampling.
2601.07094
Jan 2026Methodology
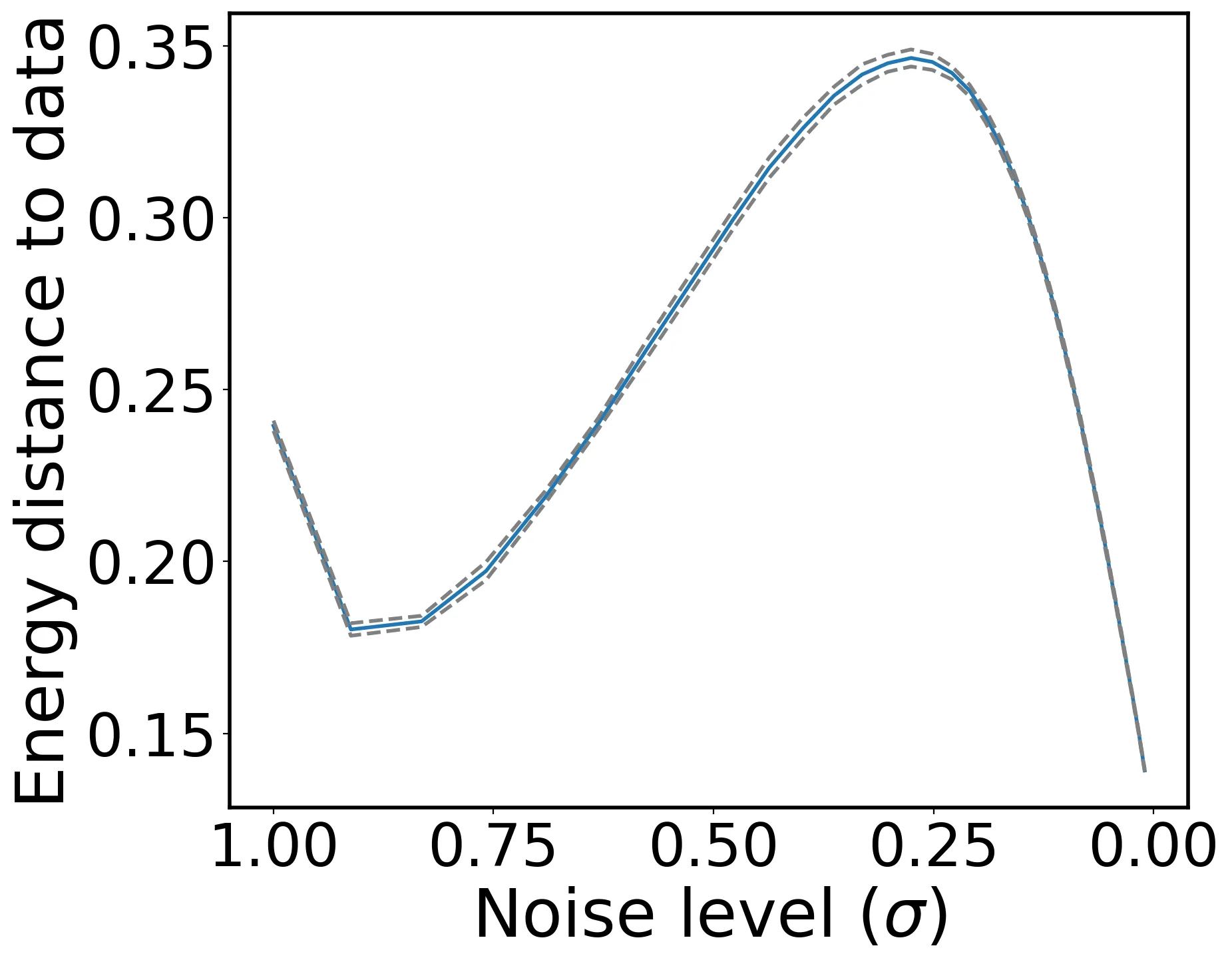
Energy-Tweedie: Score meets Score, Energy meets Energy
Denoising and score estimation have long been known to be linked via the classical Tweedie's formula. In this work, we first extend the latter to a wider range of distributions often called "energy models" and denoted elliptical distributions in this work. Next, we examine an alternative view: we consider the denoising posterior $P(X|Y)$ as the optimizer of the energy score (a scoring rule) and derive a fundamental identity that connects the (path-) derivative of a (possibly) non-Euclidean energy score to the score of the noisy marginal. This identity can be seen as an analog of Tweedie's identity for the energy score, and allows for several interesting applications; for example, score estimation, noise distribution parameter estimation, as well as using energy score models in the context of "traditional" diffusion model samplers with a wider array of noising distributions.
2512.23818
Dec 2025Statistical Learning
Probabilistic Modelling is Sufficient for Causal Inference
Causal inference is a key research area in machine learning, yet confusion reigns over the tools needed to tackle it. There are prevalent claims in the machine learning literature that you need a bespoke causal framework or notation to answer causal questions. In this paper, we want to make it clear that you \emph{can} answer any causal inference question within the realm of probabilistic modelling and inference, without causal-specific tools or notation. Through concrete examples, we demonstrate how causal questions can be tackled by writing down the probability of everything. Lastly, we reinterpret causal tools as emerging from standard probabilistic modelling and inference, elucidating their necessity and utility.
2512.23408
Dec 2025Statistical Learning

Gradient Dynamics of Attention: How Cross-Entropy Sculpts Bayesian Manifolds
Transformers empirically perform precise probabilistic reasoning in carefully constructed ``Bayesian wind tunnels'' and in large-scale language models, yet the mechanisms by which gradient-based learning creates the required internal geometry remain opaque. We provide a complete first-order analysis of how cross-entropy training reshapes attention scores and value vectors in a transformer attention head. Our core result is an \emph{advantage-based routing law} for attention scores, \[ \frac{\partial L}{\partial s_{ij}} = α_{ij}\bigl(b_{ij}-\mathbb{E}_{α_i}[b]\bigr), \qquad b_{ij} := u_i^\top v_j, \] coupled with a \emph{responsibility-weighted update} for values, \[ Δv_j = -η\sum_i α_{ij} u_i, \] where $u_i$ is the upstream gradient at position $i$ and $α_{ij}$ are attention weights. These equations induce a positive feedback loop in which routing and content specialize together: queries route more strongly to values that are above-average for their error signal, and those values are pulled toward the queries that use them. We show that this coupled specialization behaves like a two-timescale EM procedure: attention weights implement an E-step (soft responsibilities), while values implement an M-step (responsibility-weighted prototype updates), with queries and keys adjusting the hypothesis frame. Through controlled simulations, including a sticky Markov-chain task where we compare a closed-form EM-style update to standard SGD, we demonstrate that the same gradient dynamics that minimize cross-entropy also sculpt the low-dimensional manifolds identified in our companion work as implementing Bayesian inference. This yields a unified picture in which optimization (gradient flow) gives rise to geometry (Bayesian manifolds), which in turn supports function (in-context probabilistic reasoning).
2512.224733
Dec 2025Statistical Learning

Diffusion Models in Simulation-Based Inference: A Tutorial Review
Diffusion models have recently emerged as powerful learners for simulation-based inference (SBI), enabling fast and accurate estimation of latent parameters from simulated and real data. Their score-based formulation offers a flexible way to learn conditional or joint distributions over parameters and observations, thereby providing a versatile solution to various modeling problems. In this tutorial review, we synthesize recent developments on diffusion models for SBI, covering design choices for training, inference, and evaluation. We highlight opportunities created by various concepts such as guidance, score composition, flow matching, consistency models, and joint modeling. Furthermore, we discuss how efficiency and statistical accuracy are affected by noise schedules, parameterizations, and samplers. Finally, we illustrate these concepts with case studies across parameter dimensionalities, simulation budgets, and model types, and outline open questions for future research.
2512.206851
Dec 2025Statistical Learning
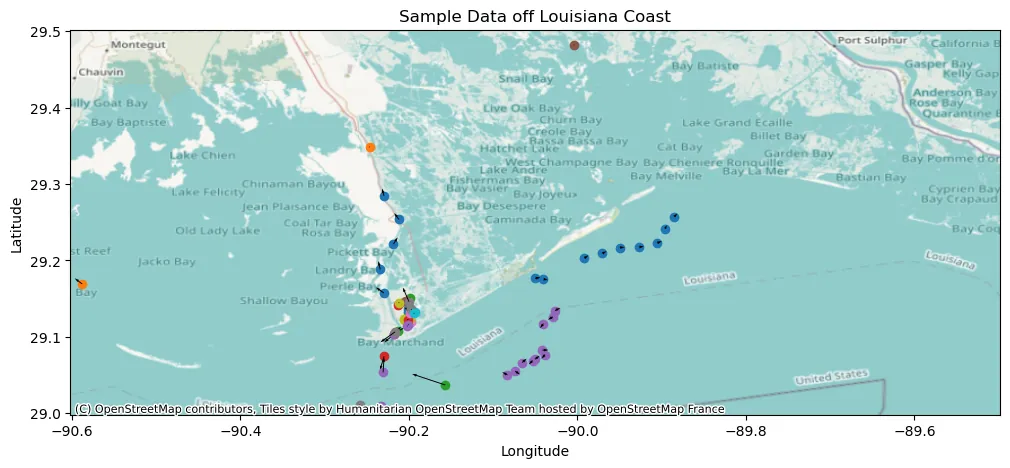
Maritime Vessel Tracking
The Automatic Identification System (AIS) provides time stamped vessel positions and kinematic reports that enable maritime authorities to monitor traffic. We consider the problem of relabeling AIS trajectories when vessel identifiers are missing, focusing on a challenging nationwide setting in which tracks are heavily downsampled and span diverse operating environments across continental U.S. waters. We propose a hybrid pipeline that first applies a physics-based screening step to project active track endpoints forward in time and select a small set of plausible ancestors for each new observation. A supervised neural classifier then chooses among these candidates, or initiates a new track, using engineered space time and kinematic consistency features. On held out data, this approach improves posit accuracy relative to unsupervised baselines, demonstrating that combining simple motion models with learned disambiguation can scale vessel relabeling to heterogeneous, high volume AIS streams.
2512.11707
Dec 2025Applications
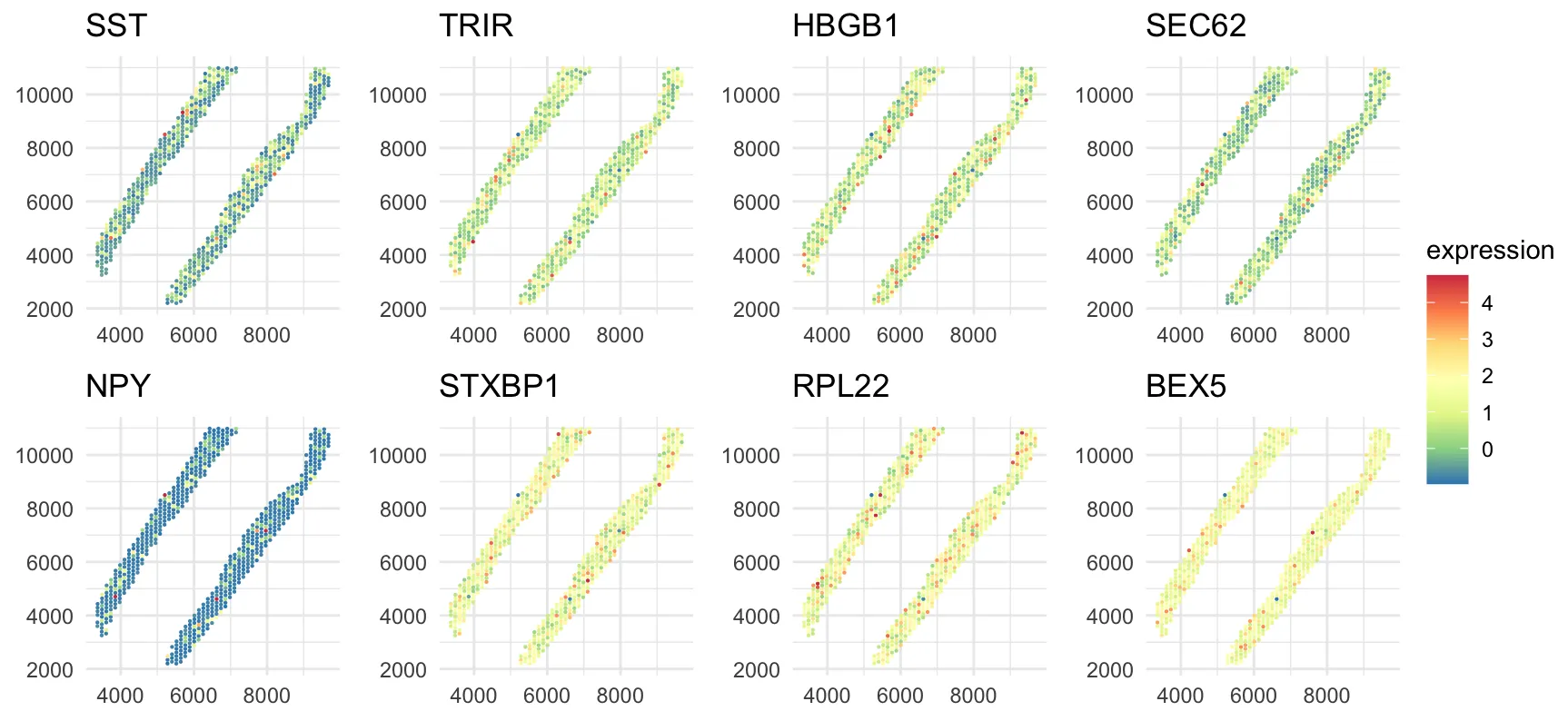
Spatially Varying Gene Regulatory Networks via Bayesian Nonparametric Covariate-Dependent Directed Cyclic Graphical Models
Spatial transcriptomics technologies enable the measurement of gene expression with spatial context, providing opportunities to understand how gene regulatory networks vary across tissue regions. However, existing graphical models focus primarily on undirected graphs or directed acyclic graphs, limiting their ability to capture feedback loops that are prevalent in gene regulation. Moreover, ensuring the so-called stability condition of cyclic graphs, while allowing graph structures to vary continuously with spatial covariates, presents significant statistical and computational challenges. We propose BNP-DCGx, a Bayesian nonparametric approach for learning spatially varying gene regulatory networks via covariate-dependent directed cyclic graphical models. Our method introduces a covariate-dependent random partition as an intermediary layer in a hierarchical model, which discretizes the covariate space into clusters with cluster-specific stable directed cyclic graphs. Through partition averaging, we obtain smoothly varying graph structures over space while maintaining theoretical guarantees of stability. We develop an efficient parallel tempered Markov chain Monte Carlo algorithm for posterior inference and demonstrate through simulations that our method accurately recovers both piecewise constant and continuously varying graph structures. Application to spatial transcriptomics data from human dorsolateral prefrontal cortex reveals spatially varying regulatory networks with feedback loops, identifies potential cell subtypes within established cell types based on distinct regulatory mechanisms, and provides new insights into spatial organization of gene regulation in brain tissue.
2512.11732
Dec 2025Methodology
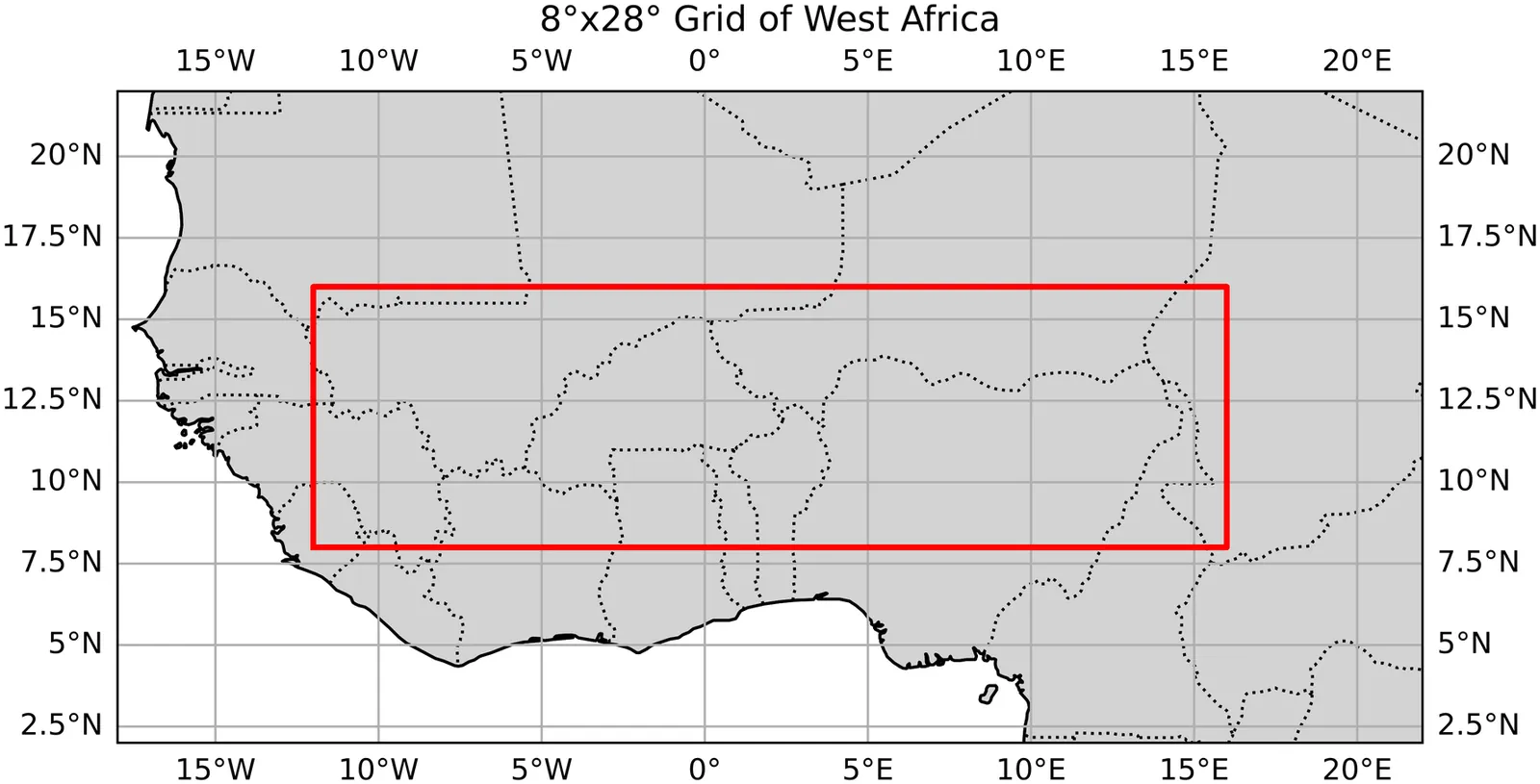
Predicting Onsets and Dry Spells of the West African Monsoon Season Using Machine Learning Methods
The beginning of the rainy season and the occurrence of dry spells in West Africa is notoriously difficult to predict, however these are the key indicators farmers use to decide when to plant crops, having a major influence on their overall yield. While many studies have shown correlations between global sea surface temperatures and characteristics of the West African monsoon season, there are few that effectively implementing this information into machine learning (ML) prediction models. In this study we investigated the best ways to define our target variables, onset and dry spell, and produced methods to predict them for upcoming seasons using sea surface temperature teleconnections. Defining our target variables required the use of a combination of two well known definitions of onset. We then applied custom statistical techniques -- like total variation regularization and predictor selection -- to the two models we constructed, the first being a linear model and the other an adaptive-threshold logistic regression model. We found mixed results for onset prediction, with spatial verification showing signs of significant skill, while temporal verification showed little to none. For dry spell though, we found significant accuracy through the analysis of multiple binary classification metrics. These models overcome some limitations that current approaches have, such as being computationally intensive and needing bias correction. We also introduce this study as a framework to use ML methods for targeted prediction of certain weather phenomenon using climatologically relevant variables. As we apply ML techniques to more problems, we see clear benefits for fields like meteorology and lay out a few new directions for further research.
2512.01965
Dec 2025Applications
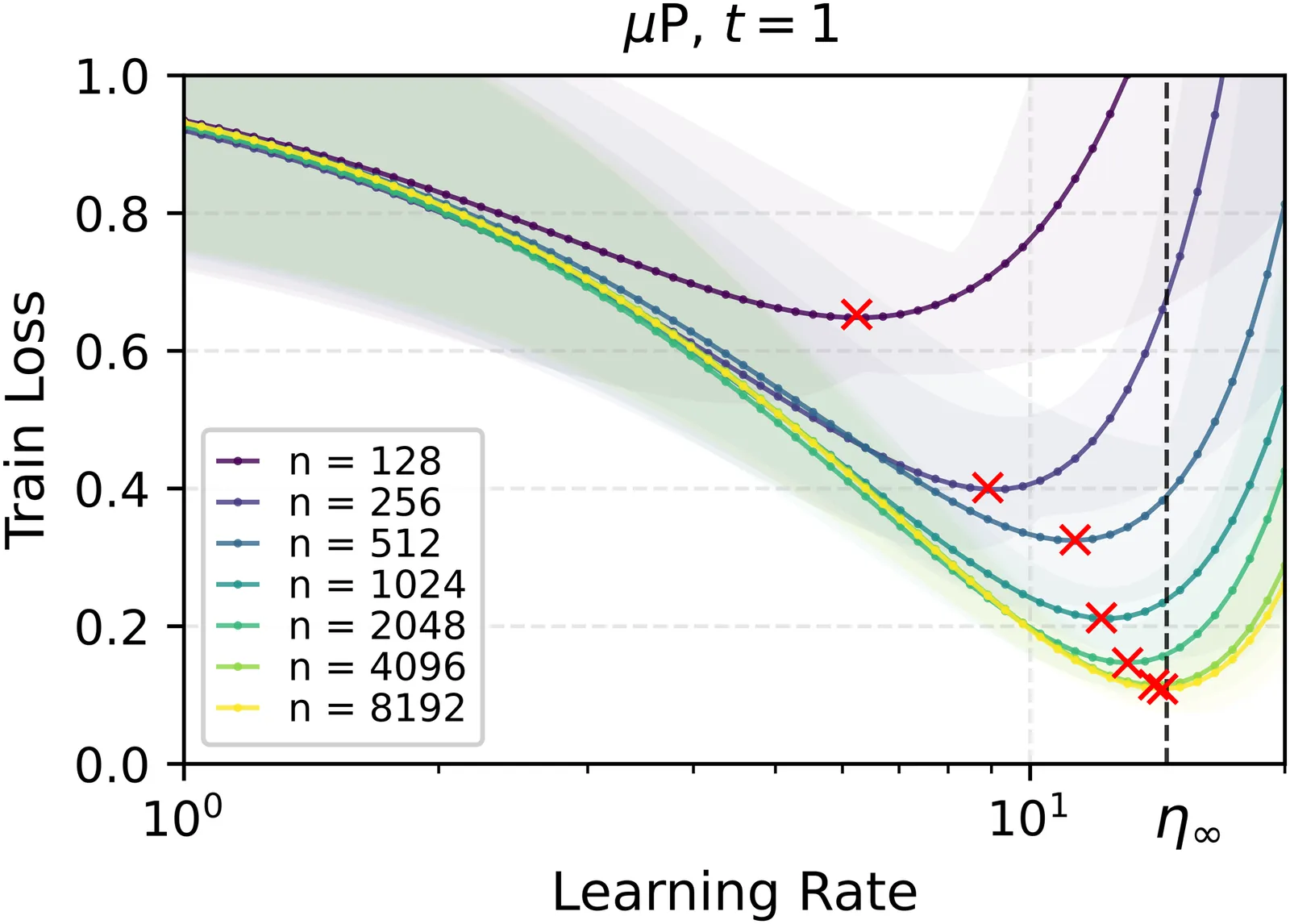
A Proof of Learning Rate Transfer under $μ$P
We provide the first proof of learning rate transfer with width in a linear multi-layer perceptron (MLP) parametrized with $\mu$P, a neural network parameterization designed to ``maximize'' feature learning in the infinite-width limit. We show that under $\mu P$, the optimal learning rate converges to a \emph{non-zero constant} as width goes to infinity, providing a theoretical explanation to learning rate transfer. In contrast, we show that this property fails to hold under alternative parametrizations such as Standard Parametrization (SP) and Neural Tangent Parametrization (NTP). We provide intuitive proofs and support the theoretical findings with extensive empirical results.
2511.017341
Nov 2025Statistical Learning