Methodology
Experimental and survey design, statistics methodology development.
Looking for a broader view? This category is part of:
Experimental and survey design, statistics methodology development.
Looking for a broader view? This category is part of:
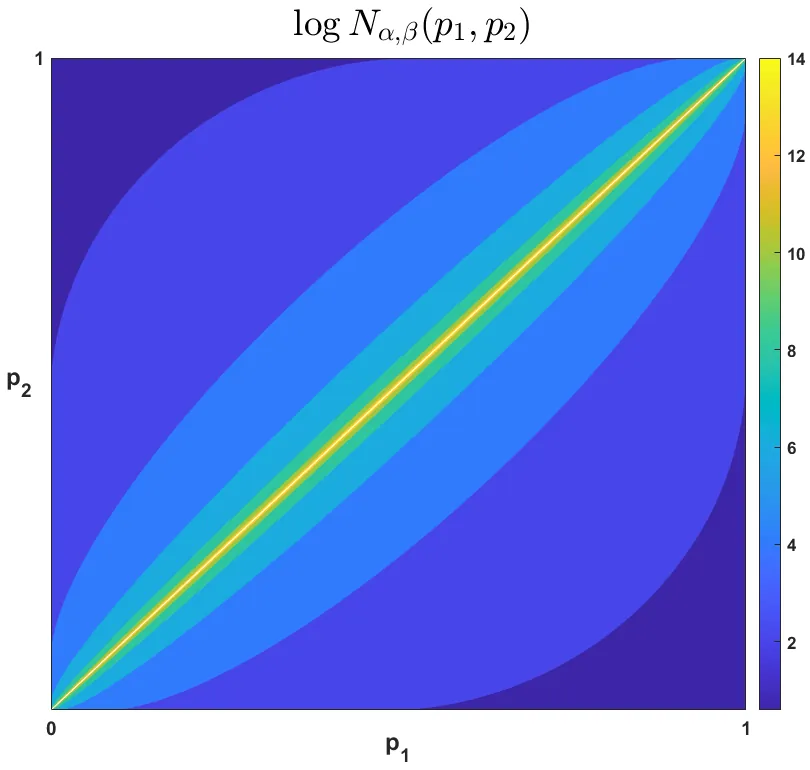
We propose the use of a simple intuitive principle for measuring algorithmic classification bias: the significance of the differences in a classifier's error rates across the various demographics is inversely commensurate with the sample size required to statistically detect them. That is, if large sample sizes are required to statistically establish biased behavior, the algorithm is less biased, and vice versa. In a simple setting, we assume two distinct demographics, and non-parametric estimates of the error rates on them, e1 and e2, respectively. We use a well-known approximate formula for the sample size of the chi-squared test, and verify some basic desirable properties of the proposed measure. Next, we compare the proposed measure with two other commonly used statistics, the difference e2-e1 and the ratio e2/e1 of the error rates. We establish that the proposed measure is essentially different in that it can rank algorithms for bias differently, and we discuss some of its advantages over the other two measures. Finally, we briefly discuss how some of the desirable properties of the proposed measure emanate from fundamental characteristics of the method, rather than the approximate sample size formula we used, and thus, are expected to hold in more complex settings with more than two demographics.
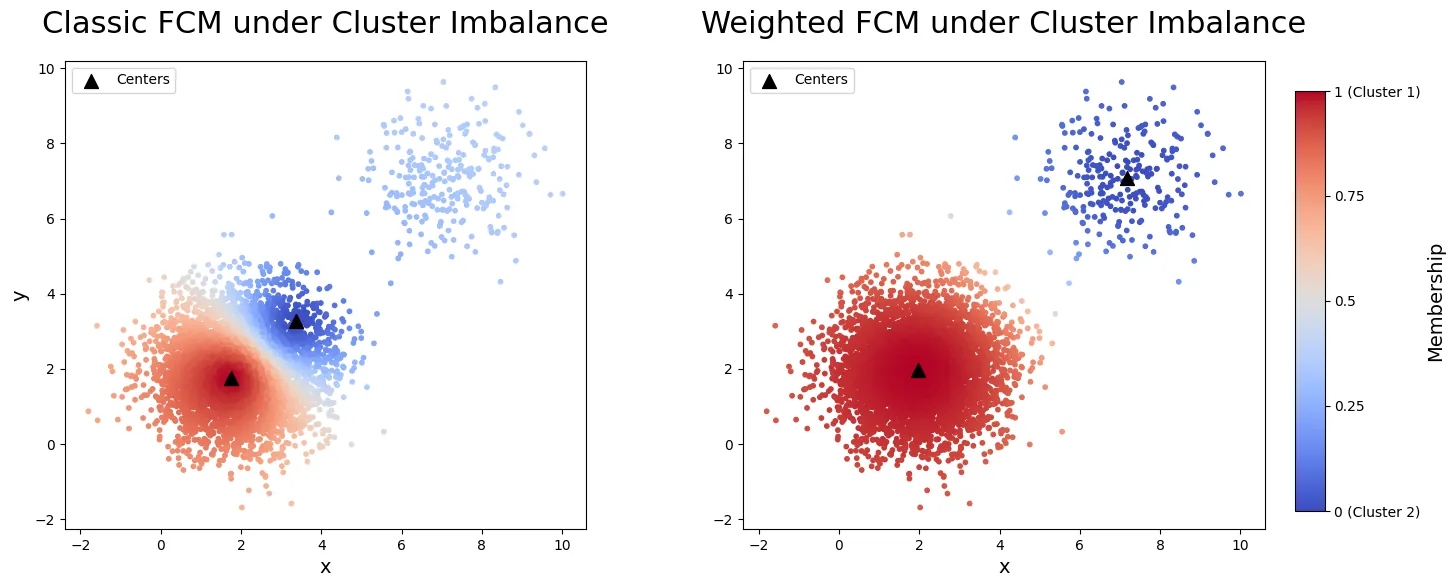
Clustering is a central tool in biomedical research for discovering heterogeneous patient subpopulations, where group boundaries are often diffuse rather than sharply separated. Traditional methods produce hard partitions, whereas soft clustering methods such as fuzzy $c$-means (FCM) allow mixed memberships and better capture uncertainty and gradual transitions. Despite the widespread use of FCM, principled statistical inference for fuzzy clustering remains limited. We develop a new framework for weighted fuzzy $c$-means (WFCM) for settings with potential cluster size imbalance. Cluster-specific weights rebalance the classical FCM criterion so that smaller clusters are not overwhelmed by dominant groups, and the weighted objective induces a normalized density model with scale parameter $σ$ and fuzziness parameter $m$. Estimation is performed via a blockwise majorize--minimize (MM) procedure that alternates closed-form membership and centroid updates with likelihood-based updates of $(σ,\bw)$. The intractable normalizing constant is approximated by importance sampling using a data-adaptive Gaussian mixture proposal. We further provide likelihood ratio tests for comparing cluster centers and bootstrap-based confidence intervals. We establish consistency and asymptotic normality of the maximum likelihood estimator, validate the method through simulations, and illustrate it using single-cell RNA-seq and Alzheimer disease Neuroimaging Initiative (ADNI) data. These applications demonstrate stable uncertainty quantification and biologically meaningful soft memberships, ranging from well-separated cell populations under imbalance to a graded AD versus non-AD continuum consistent with disease progression.
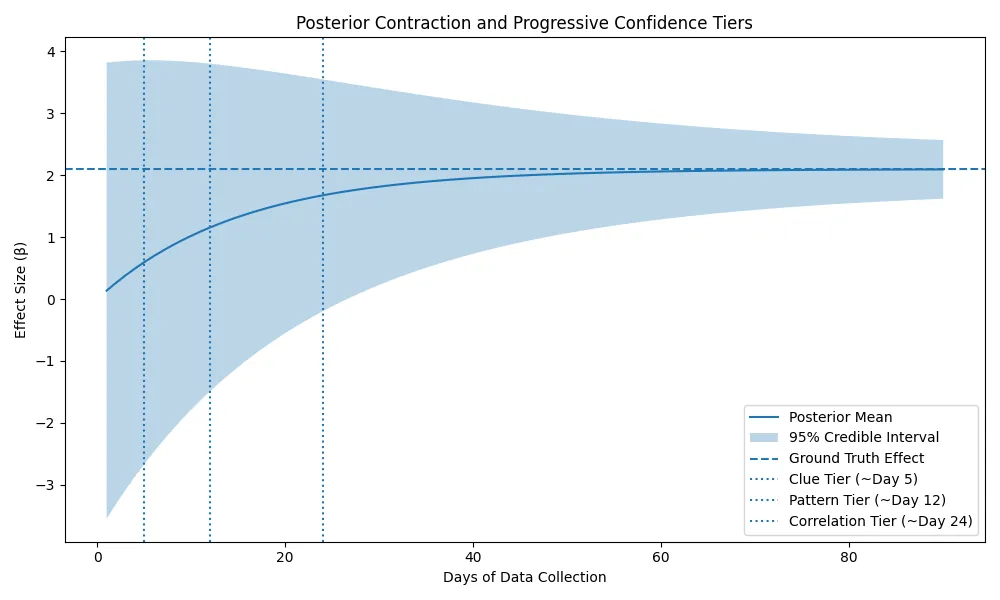
Personal health analytics systems face a persistent cold-start dilemma: users expect meaningful insights early in data collection, while conventional statistical inference requires data volumes that often exceed engagement horizons. Existing approaches either delay inference until fixed statistical thresholds are met -- leading to user disengagement -- or surface heuristic insights without formal uncertainty quantification, risking false confidence. We propose a progressive Bayesian confidence architecture that formalizes early-stage inference through phased interpretation of posterior uncertainty. Drawing on Bayesian updating and epistemic strategies from financial risk modeling under sparse observations, we map posterior contraction to interpretable tiers of insight, ranging from exploratory directional evidence to robust associative inference. We demonstrate the framework's performance through controlled experimentation with synthetic N-of-1 health data, showing that calibrated early insights can be generated within 5--7 days while maintaining explicit epistemic humility. Compared to fixed-threshold baselines requiring 30+ days of data, the proposed approach yields earlier directional signals (mean: 5.3 vs 31.7 days, p<0.001) while controlling false discovery rates below 6% (5.9% at day 30) despite 26-day earlier detection, compared to 0% FDR for fixed-threshold baselines that delay insights by 30 days. In addition, we show strong uncertainty calibration (76% credible interval coverage for ground-truth correlations at day 90). This work contributes a methodological framework for uncertainty-aware early inference in personalized health analytics that bridges the gap between user engagement requirements and statistical rigor.
 2601.02640
2601.02640We propose the first approach for multiple multivariate density-density regression (MDDR), making it possible to consider the regression of a multivariate density-valued response on multiple multivariate density-valued predictors. The core idea is to define a fitted distribution using a sliced Wasserstein barycenter (SWB) of push-forwards of the predictors and to quantify deviations from the observed response using the sliced Wasserstein (SW) distance. Regression functions, which map predictors' supports to the response support, and barycenter weights are inferred within a generalized Bayes framework, enabling principled uncertainty quantification without requiring a fully specified likelihood. The inference process can be seen as an instance of an inverse SWB problem. We establish theoretical guarantees, including the stability of the SWB under perturbations of marginals and barycenter weights, sample complexity of the generalized likelihood, and posterior consistency. For practical inference, we introduce a differentiable approximation of the SWB and a smooth reparameterization to handle the simplex constraint on barycenter weights, allowing efficient gradient-based MCMC sampling. We demonstrate MDDR in an application to inference for population-scale single-cell data. Posterior analysis under the MDDR model in this example includes inference on communication between multiple source/sender cell types and a target/receiver cell type. The proposed approach provides accurate fits, reliable predictions, and interpretable posterior estimates of barycenter weights, which can be used to construct sparse cell-cell communication networks.

Conformal novelty detection is a classical machine learning task for which uncertainty quantification is essential for providing reliable results. Recent work has shown that the BH procedure applied to conformal p-values controls the false discovery rate (FDR). Unfortunately, the BH procedure can lead to over-optimistic assessments near the rejection threshold, with an increase of false discoveries at the margin as pointed out by Soloff et al. (2024). This issue is solved therein by the support line (SL) correction, which is proven to control the boundary false discovery rate (bFDR) in the independent, non-conformal setting. The present work extends the SL method to the conformal setting: first, we show that the SL procedure can violate the bFDR control in this specific setting. Second, we propose several alternatives that provably control the bFDR in the conformal setting. Finally, numerical experiments with both synthetic and real data support our theoretical findings and show the relevance of the new proposed procedures.
We propose a novel finite-sample procedure for testing composite null hypotheses. Traditional likelihood ratio tests based on asymptotic $χ^2$ approximations often exhibit substantial bias in small samples. Our procedure rejects the composite null hypothesis $H_0: θ\in Θ_0$ if the simple null hypothesis $H_0: θ= θ_t$ is rejected for every $θ_t$ in the null region $Θ_0$, using an inflated significance level. We derive formulas that determine this inflated level so that the overall test approximately maintains the desired significance level even with small samples. Whereas the traditional likelihood ratio test applies when the null region is defined solely by equality constraints--that is, when it forms a manifold without boundary--the proposed approach extends to null hypotheses defined by both equality and inequality constraints. In addition, it accommodates null hypotheses expressed as unions of several component regions and can be applied to models involving nuisance parameters. Through several examples featuring nonstandard composite null hypotheses, we demonstrate numerically that the proposed test achieves accurate inference, exhibiting only a small gap between the actual and nominal significance levels for both small and large samples.
Out-of-distribution (OOD) prediction is often approached by restricting models to causal or invariant covariates, avoiding non-causal spurious associations that may be unstable across environments. Despite its theoretical appeal, this strategy frequently underperforms empirical risk minimization (ERM) in practice. We investigate the source of this gap and show that such failures naturally arise when only a subset of the true causes of the outcome is observed. In these settings, non-causal spurious covariates can serve as informative proxies for unobserved causes and substantially improve prediction, except under distribution shifts that break these proxy relationships. Consequently, the optimal set of predictive covariates is neither universal nor necessarily exhibits invariant relationships with the outcome across all environments, but instead depends on the specific type of shift encountered. Crucially, we observe that different covariate shifts induce distinct, observable signatures in the covariate distribution itself. Moreover, these signatures can be extracted from unlabeled data in the target OOD environment and used to assess when proxy covariates remain reliable and when they fail. Building on this observation, we propose an environment-adaptive covariate selection (EACS) algorithm that maps environment-level covariate summaries to environment-specific covariate sets, while allowing the incorporation of prior causal knowledge as constraints. Across simulations and applied datasets, EACS consistently outperforms static causal, invariant, and ERM-based predictors under diverse distribution shifts.
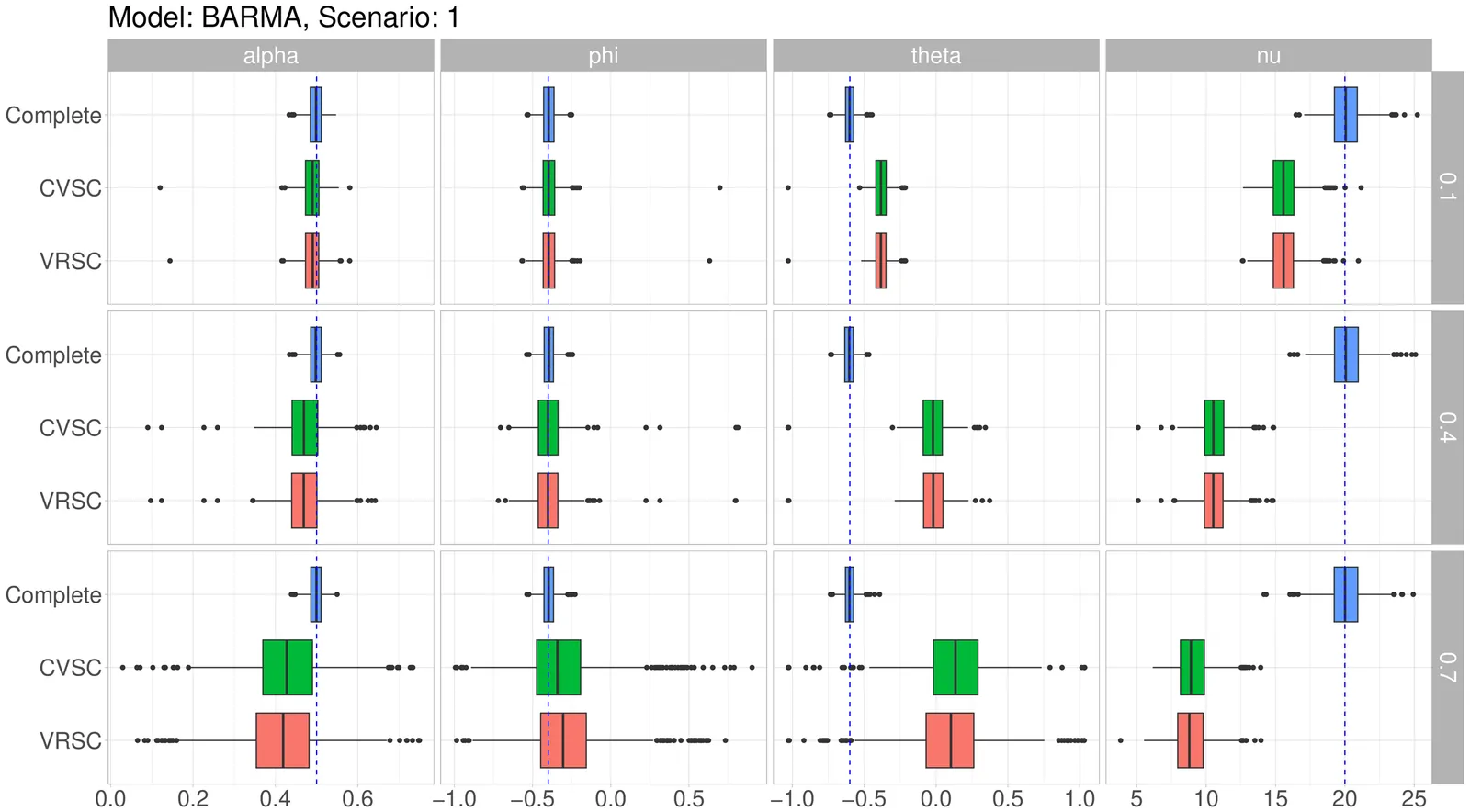
Handling missing data in time series is a complex problem due to the presence of temporal dependence. General-purpose imputation methods, while widely used, often distort key statistical properties of the data, such as variance and dependence structure, leading to biased estimation and misleading inference. These issues become more pronounced in models that explicitly rely on capturing serial dependence, as standard imputation techniques fail to preserve the underlying dynamics. This paper proposes a novel multiple imputation method specifically designed for parameter estimation in observation-driven models (ODM). The approach takes advantage of the iterative nature of the systematic component in ODM to propagate the dependence structure through missing data, minimizing its impact on estimation. Unlike traditional imputation techniques, the proposed method accommodates continuous, discrete, and mixed-type data while preserving key distributional and dependence properties. We evaluate its performance through Monte Carlo simulations in the context of GARMA models, considering time series with up to 70\% missing data. An application to the proportion of stocked energy stored in South Brazil further demonstrates its practical utility.
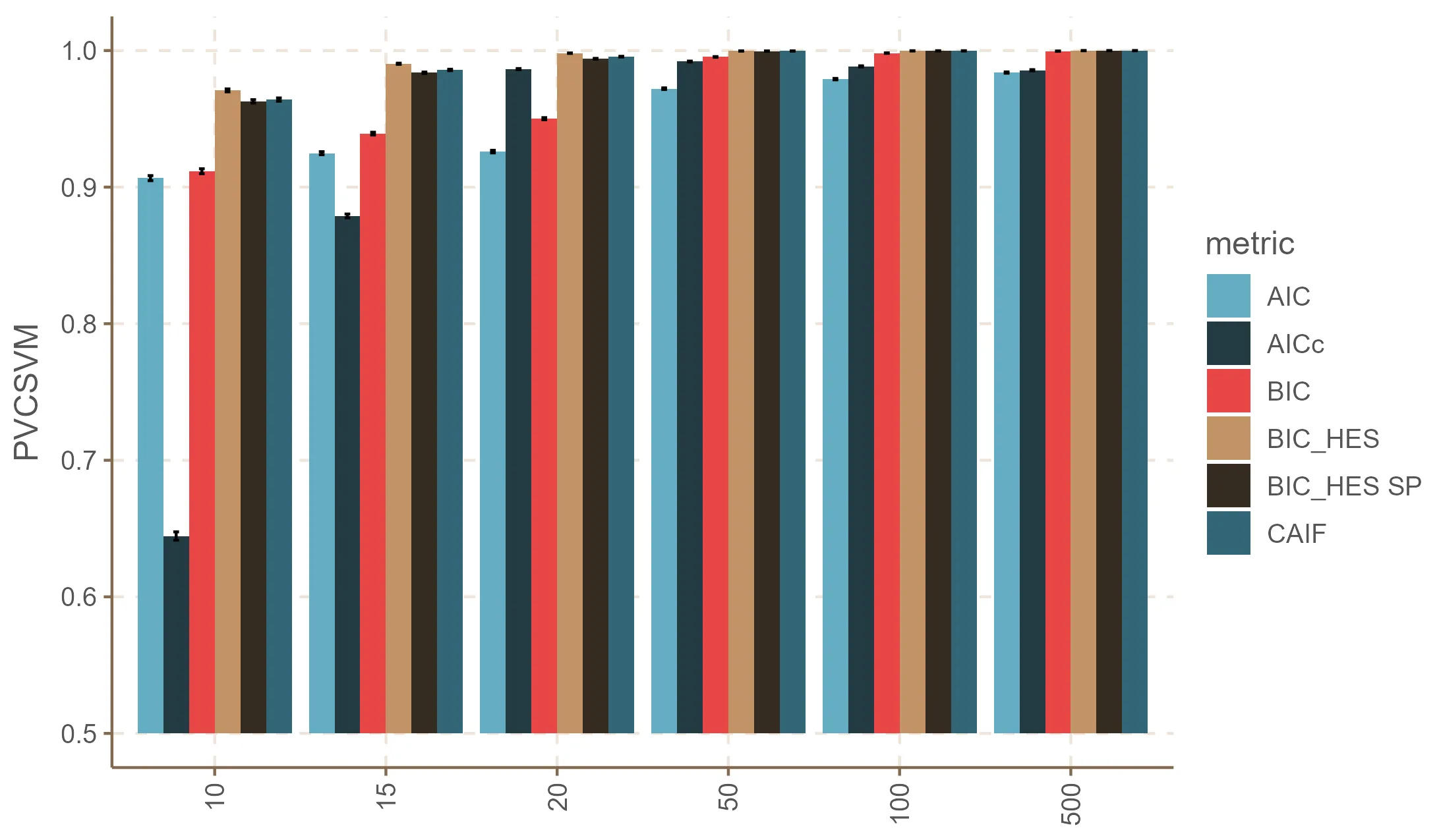
In this work, we propose a modified Bayesian Information Criterion (BIC) specifically designed for mixture models and hierarchical structures. This criterion incorporates the determinant of the Hessian matrix of the log-likelihood function, thereby refining the classical Bayes Factor by accounting for the curvature of the likelihood surface. Such geometric information introduces a more nuanced penalization for model complexity. The proposed approach improves model selection, particularly under small-sample conditions or in the presence of noise variables. Through theoretical derivations and extensive simulation studies-including both linear and linear mixed models-we show that our criterion consistently outperforms traditional methods such as BIC, Akaike Information Criterion (AIC), and related variants. The results suggest that integrating curvature-based information from the likelihood landscape leads to more robust and accurate model discrimination in complex data environments.
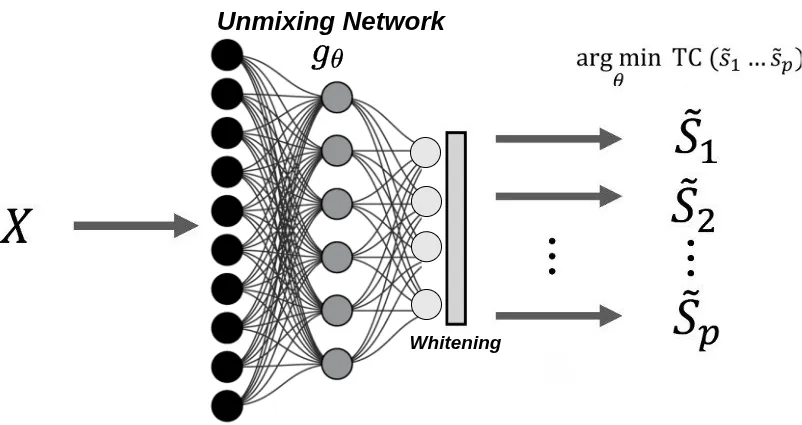
Blind source separation, particularly through independent component analysis (ICA), is widely utilized across various signal processing domains for disentangling underlying components from observed mixed signals, owing to its fully data-driven nature that minimizes reliance on prior assumptions. However, conventional ICA methods rely on an assumption of linear mixing, limiting their ability to capture complex nonlinear relationships and to maintain robustness in noisy environments. In this work, we present deep deterministic nonlinear independent component analysis (DDICA), a novel deep neural network-based framework designed to address these limitations. DDICA leverages a matrix-based entropy function to directly optimize the independence criterion via stochastic gradient descent, bypassing the need for variational approximations or adversarial schemes. This results in a streamlined training process and improved resilience to noise. We validated the effectiveness and generalizability of DDICA across a range of applications, including simulated signal mixtures, hyperspectral image unmixing, modeling of primary visual receptive fields, and resting-state functional magnetic resonance imaging (fMRI) data analysis. Experimental results demonstrate that DDICA effectively separates independent components with high accuracy across a range of applications. These findings suggest that DDICA offers a robust and versatile solution for blind source separation in diverse signal processing tasks.
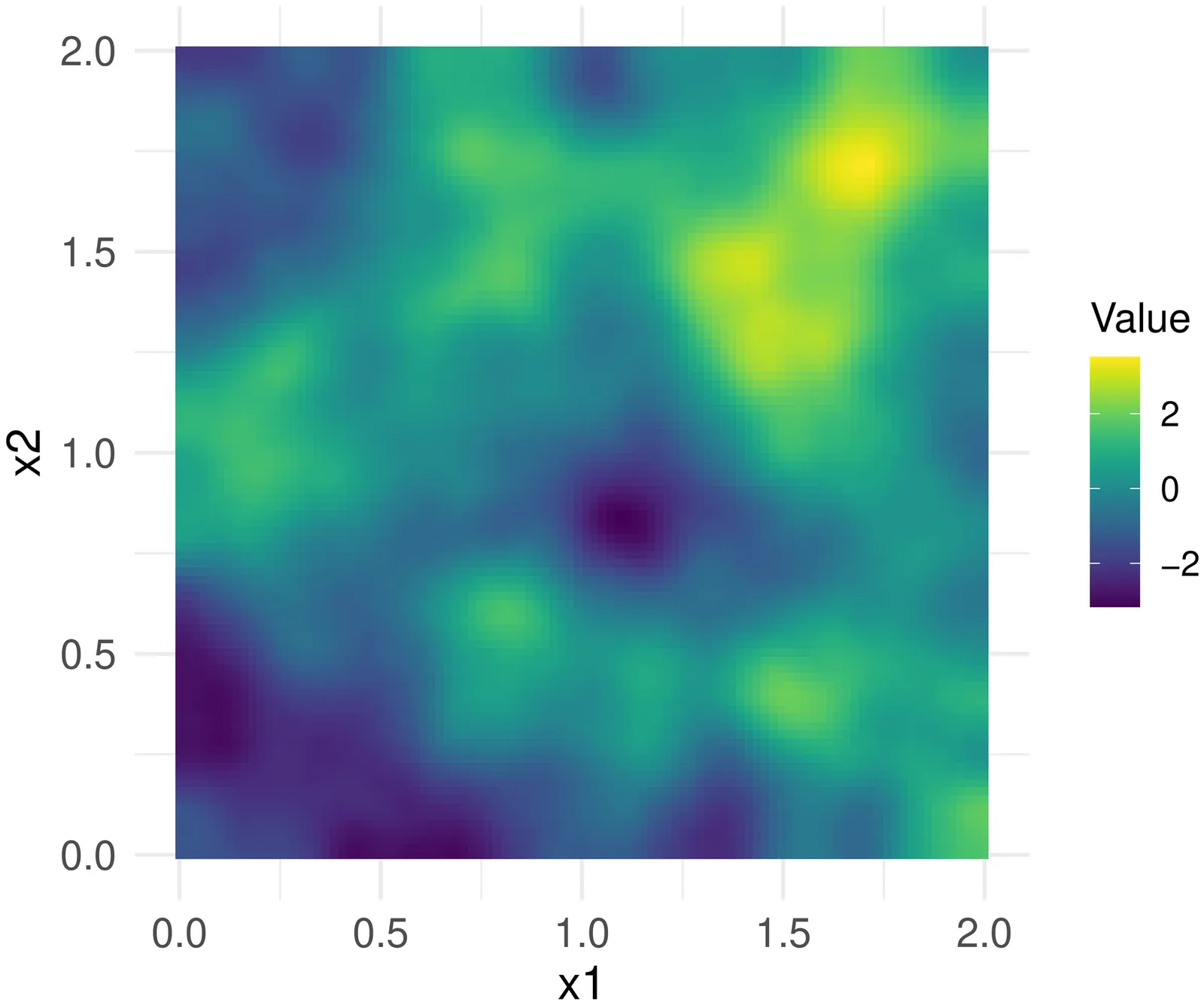
Intrinsic Gaussian fields are used in many areas of statistics as models for spatial or spatio-temporal dependence, or as priors for latent variables. However, there are two major gaps in the literature: first, the number and flexibility of existing intrinsic models are very limited; second, theory, fast inference, and software are currently underdeveloped for intrinsic fields. We tackle these challenges by introducing the new flexible class of intrinsic Whittle--Matérn Gaussian random fields obtained as the solution to a stochastic partial differential equation (SPDE). Exploiting sparsity resulting from finite-element approximations, we develop fast estimation and simulation methods for these models. We demonstrate the benefits of this intrinsic SPDE approach for the important task of kriging under extrapolation settings. Leveraging the connection of intrinsic fields to spatial extreme value processes, we translate our theory to an SPDE approach for Brown--Resnick processes for sparse modeling of spatial extreme events. This new paradigm paves the way for efficient inference in unprecedented dimensions. To demonstrate the wide applicability of our new methodology, we apply it in two very different areas: a longitudinal study of renal function data, and the modeling of marine heat waves using high-resolution sea surface temperature data.
We introduce a nonparametric model for time-evolving, unobserved probability distributions from discrete-time data consisting of unlabelled partitions. The latent process is a two-parameter Poisson-Dirichlet diffusion, and observations arise via exchangeable sampling. Applications include social and genetic data where only aggregate clustering summaries are observed. To address the intractable likelihood, we develop a tractable inferential framework that avoids label enumeration and direct simulation of the latent state. We exploit a duality between the diffusion and a pure-death process on partitions, together with coagulation operators that encode the effect of new data. These yield closed-form, recursive updates for forward and backward inference. We compute exact posterior distributions of the latent state at arbitrary times and predictive distributions of future or interpolated partitions. This enables online and offline inference and forecasting with full uncertainty quantification, bypassing MCMC and sequential Monte Carlo. Compared to particle filtering, our method achieves higher accuracy, lower variance, and substantial computational gains. We illustrate the methodology with synthetic experiments and a social network application, recovering interpretable patterns in time-varying heterozygosity.
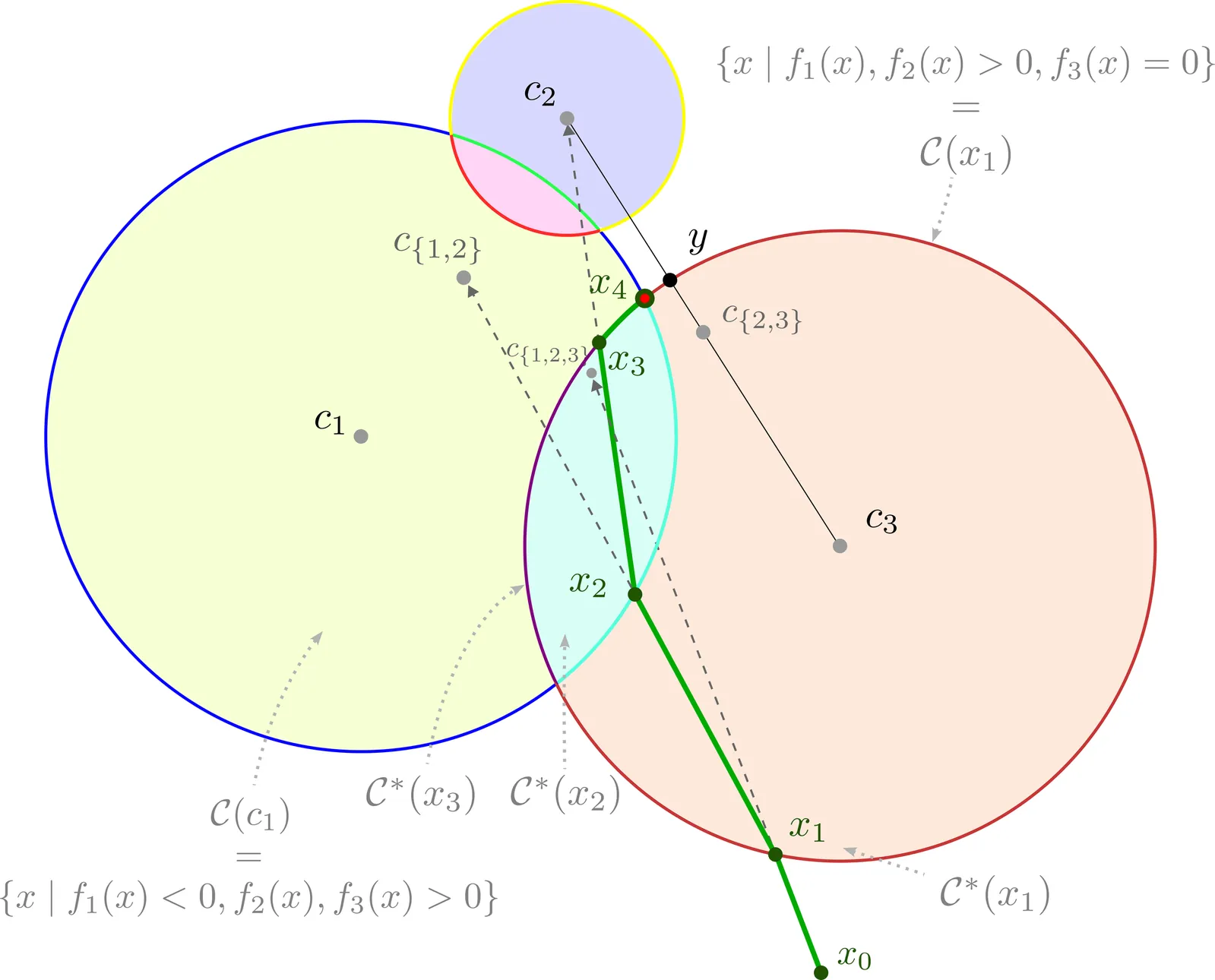
A parametric cluster model is a statistical model providing geometric insights onto the points defining a cluster. The {\em spherical cluster model} (SC) approximates a finite point set $P\subset \mathbb{R}^d$ by a sphere $S(c,r)$ as follows. Taking $r$ as a fraction $η\in(0,1)$ (hyper-parameter) of the std deviation of distances between the center $c$ and the data points, the cost of the SC model is the sum over all data points lying outside the sphere $S$ of their power distance with respect to $S$. The center $c$ of the SC model is the point minimizing this cost. Note that $η=0$ yields the celebrated center of mass used in KMeans clustering. We make three contributions. First, we show fitting a spherical cluster yields a strictly convex but not smooth combinatorial optimization problem. Second, we present an exact solver using the Clarke gradient on a suitable stratified cell complex defined from an arrangement of hyper-spheres. Finally, we present experiments on a variety of datasets ranging in dimension from $d=9$ to $d=10,000$, with two main observations. First, the exact algorithm is orders of magnitude faster than BFGS based heuristics for datasets of small/intermediate dimension and small values of $η$, and for high dimensional datasets (say $d>100$) whatever the value of $η$. Second, the center of the SC model behave as a parameterized high-dimensional median. The SC model is of direct interest for high dimensional multivariate data analysis, and the application to the design of mixtures of SC will be reported in a companion paper.

Sensitivity analysis informs causal inference by assessing the sensitivity of conclusions to departures from assumptions. The consistency assumption states that there are no hidden versions of treatment and that the outcome arising naturally equals the outcome arising from intervention. When reasoning about the possibility of consistency violations, it can be helpful to distinguish between covariates and versions of treatment. In the context of surgery, for example, genomic variables are covariates and the skill of a particular surgeon is a version of treatment. There may be hidden versions of treatment, and this paper addresses that concern with a new kind of sensitivity analysis. Whereas many methods for sensitivity analysis are focused on confounding by unmeasured covariates, the methodology of this paper is focused on confounding by hidden versions of treatment. In this paper, new mathematical notation is introduced to support the novel method, and example applications are described.
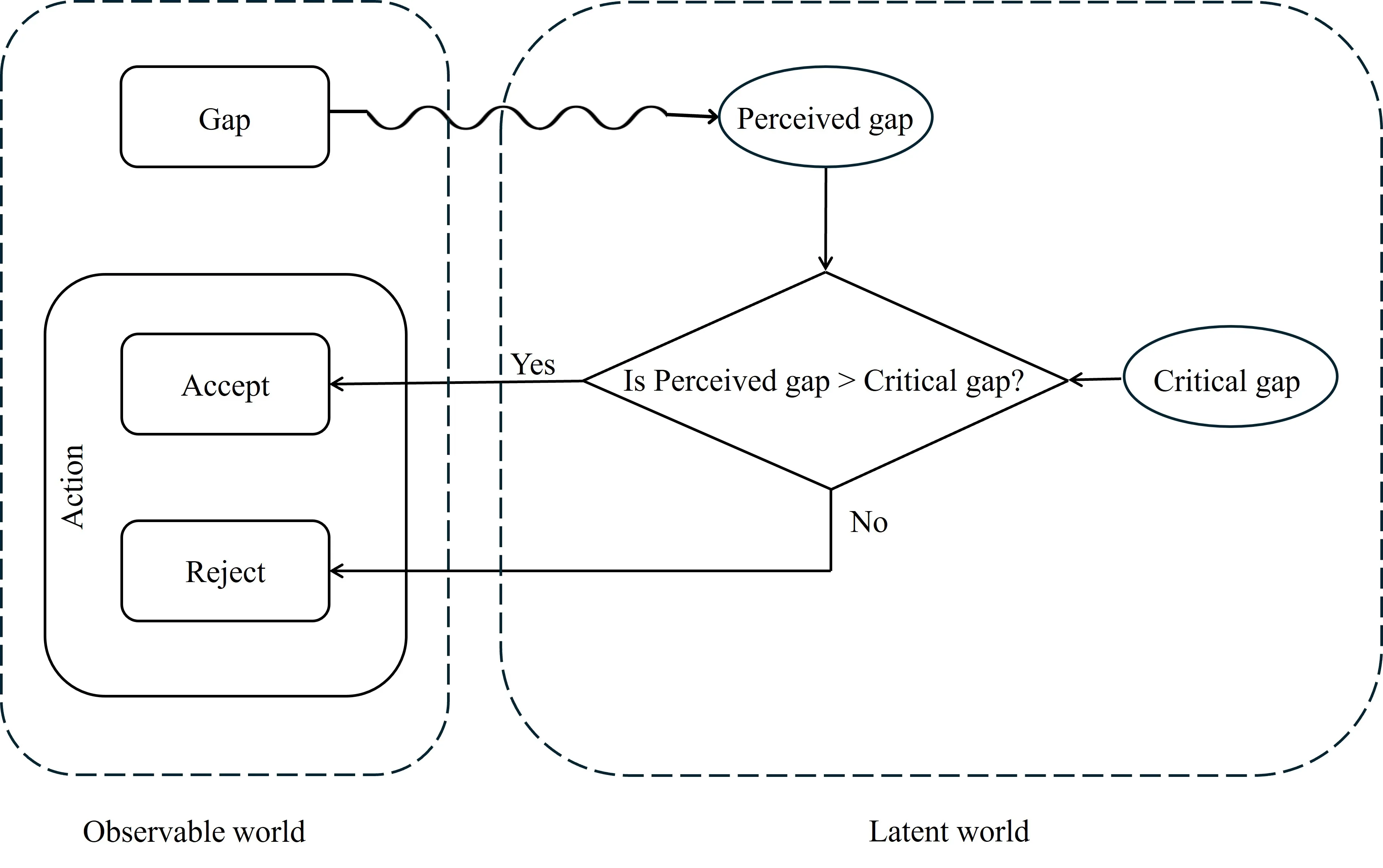
This work on gap acceptance is based on the premise that the decision to accept/reject a gap happens in a person's mind and therefore must be based on the perceived gap and not the measured gap. The critical gap must also exist in a person's mind and hence, together with the perceived gap, is a latent variable. Finally, it is also proposed that the critical gap is influenced by various exogenous variables such as subject and opposing vehicle types, and perceived waiting time. Mathematical models that (i) incorporate systematic and random distortions during the perception process and (ii) account for the effect of the various influencing variables are developed. The parameters of these models are estimated for two different gap acceptance data sets using the maximum likelihood technique. The data is collected as part of this study. The estimated parameters throw valuable insights into how these influencing variables affect the critical gap. The results corroborate the initial predictions on the nature of influence these variables must exert and give strength to the gap acceptance decision-making construct proposed here. This work also proposes a methodology to estimate a measurable/observable world emulator of the latent variable critical gap. The use of the emulator critical gap provides improved estimates of derived quantities like the average waiting time of subject vehicles. Finally, studies are also conducted to show that the number of rejected gaps can work as a reasonable surrogate for the influencing variable, waiting time.
 2512.18924
2512.18924This paper considers the problem of testing for latent structure in large symmetric data matrices. The goal here is to develop statistically principled methodology that is flexible in its applicability, computationally efficient, and insensitive to extreme data variation, thereby overcoming limitations facing existing approaches. To do so, we introduce and systematically study certain symmetric matrices, called Wilcoxon--Wigner random matrices, whose entries are normalized rank statistics derived from an underlying independent and identically distributed sample of absolutely continuous random variables. These matrices naturally arise as the matricization of one-sample problems in statistics and conceptually lie at the interface of nonparametrics, multivariate analysis, and data reduction. Among our results, we establish that the leading eigenvalue and corresponding eigenvector of Wilcoxon--Wigner random matrices admit asymptotically Gaussian fluctuations with explicit centering and scaling terms. These asymptotic results enable rigorous parameter-free and distribution-free spectral methodology for addressing two hypothesis testing problems, namely community detection and principal submatrix detection. Numerical examples illustrate the performance of the proposed approach. Throughout, our findings are juxtaposed with existing results based on the spectral properties of independent entry symmetric random matrices in signal-plus-noise data settings.
Observational studies in fields such as epidemiology often rely on covariate adjustment to estimate causal effects. Classical graphical criteria, like the back-door criterion and the generalized adjustment criterion, are powerful tools for identifying valid adjustment sets in directed acyclic graphs (DAGs). However, these criteria are not directly applicable to summary causal graphs (SCGs), which are abstractions of DAGs commonly used in dynamic systems. In SCGs, each node typically represents an entire time series and may involve cycles, making classical criteria inapplicable for identifying causal effects. Recent work established complete conditions for determining whether the micro causal effect of a treatment or an exposure $X_{t-γ}$ on an outcome $Y_t$ is identifiable via covariate adjustment in SCGs, under the assumption of no hidden confounding. However, these identifiability conditions have two main limitations. First, they are complex, relying on cumbersome definitions and requiring the enumeration of multiple paths in the SCG, which can be computationally expensive. Second, when these conditions are satisfied, they only provide two valid adjustment sets, limiting flexibility in practical applications. In this paper, we propose an equivalent but simpler formulation of those identifiability conditions and introduce a new criterion that identifies a broader class of valid adjustment sets in SCGs. Additionally, we characterize the quasi-optimal adjustment set among these, i.e., the one that minimizes the asymptotic variance of the causal effect estimator. Our contributions offer both theoretical advancement and practical tools for more flexible and efficient causal inference in abstracted causal graphs.
This is the monograph on the theory and applications of copula entropy (CE). This book first introduces the theory of CE, including its background, definition, theorems, properties, and estimation methods. The theoretical applications of CE to structure learning, association discovery, variable selection, causal discovery, system identification, time lag estimation, domain adaptation, multivariate normality test, copula hypothesis test, two-sample test, change point detection, and symmetry test are reviewed. The relationships between the theoretical applications and their connections to correlation and causality are discussed. The framework based on CE for measuring statistical independence and conditional independence is compared to the other similar ones. The advantages of CE based methodologies over the other comparable ones are evaluated with simulations. The mathematical generalizations of CE are reviewed. The real applications of CE to every branch of science and engineering are briefly introduced.
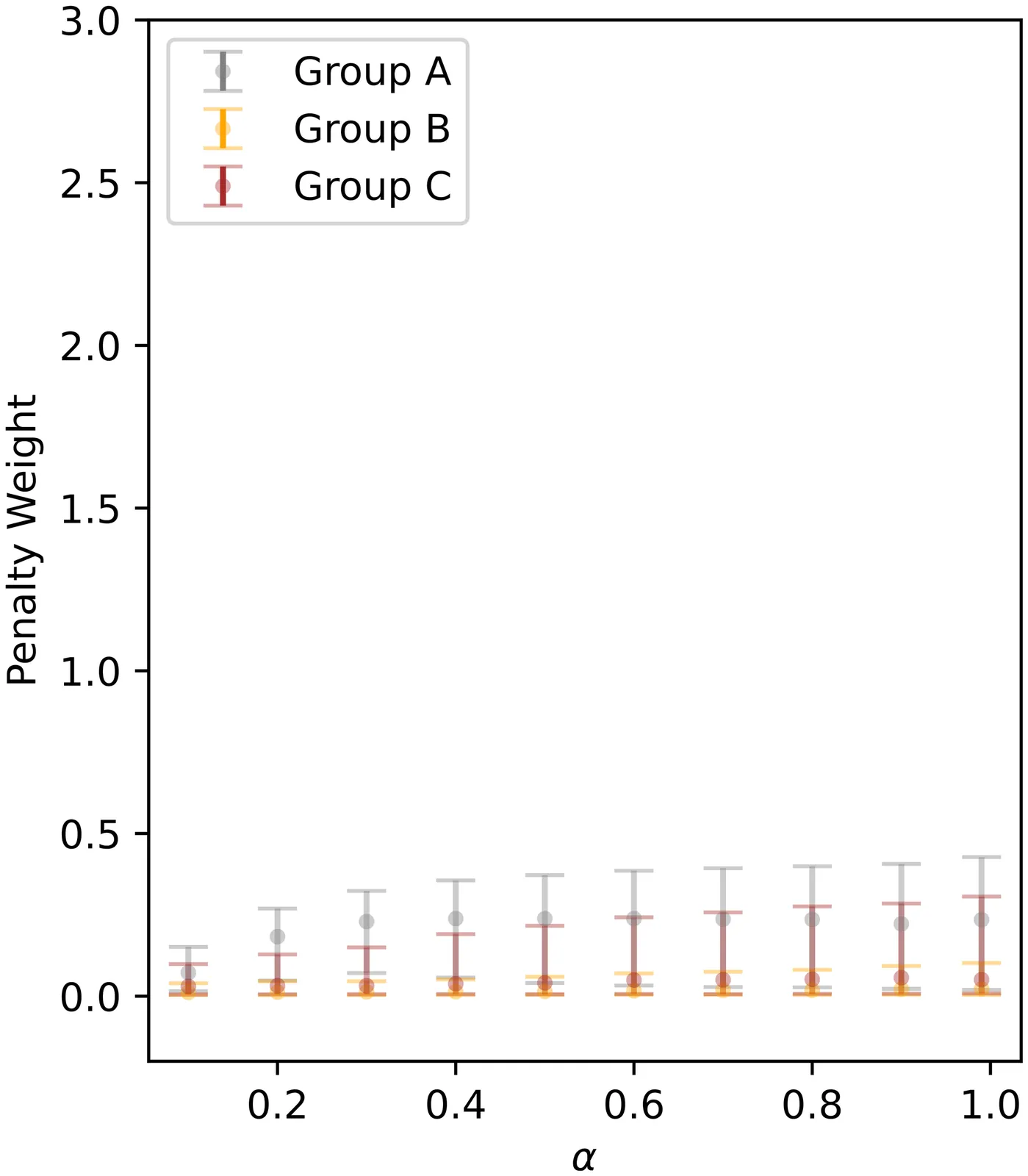
Fair regression methods have the potential to mitigate societal bias concerns in health care, but there has been little work on penalized fair regression when multiple groups experience such bias. We propose a general regression framework that addresses this gap with unfairness penalties for multiple groups. Our approach is demonstrated for binary outcomes with true positive rate disparity penalties. It can be efficiently implemented through reduction to a cost-sensitive classification problem. We additionally introduce novel score functions for automatically selecting penalty weights. Our penalized fair regression methods are empirically studied in simulations, where they achieve a fairness-accuracy frontier beyond that of existing comparison methods. Finally, we apply these methods to a national multi-site primary care study of chronic kidney disease to develop a fair classifier for end-stage renal disease. There we find substantial improvements in fairness for multiple race and ethnicity groups who experience societal bias in the health care system without any appreciable loss in overall fit.
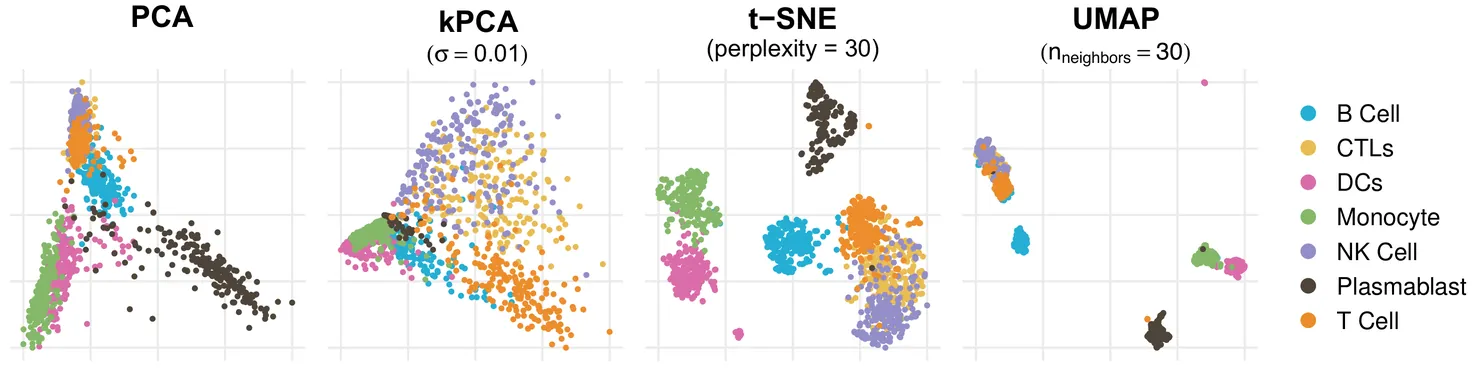
A plethora of dimension reduction methods have been developed to visualize high-dimensional data in low dimensions. However, different dimension reduction methods often output different and possibly conflicting visualizations of the same data. This problem is further exacerbated by the choice of hyperparameters, which may substantially impact the resulting visualization. To obtain a more robust and trustworthy dimension reduction output, we advocate for a consensus approach, which summarizes multiple visualizations into a single consensus dimension reduction visualization. Here, we leverage ideas from multi-view learning in order to identify the patterns that are most stable or shared across the many different dimension reduction visualizations, or views, and subsequently visualize this shared structure in a single low-dimensional plot. We demonstrate that this consensus visualization effectively identifies and preserves the shared low-dimensional data structure through both simulated and real-world case studies. We further highlight our method's robustness to the choice of dimension reduction method and hyperparameters -- a highly-desirable property when working towards trustworthy and reproducible data science.