Computation
Algorithms, simulation, graphics, visualization, software development.
Algorithms, simulation, graphics, visualization, software development.
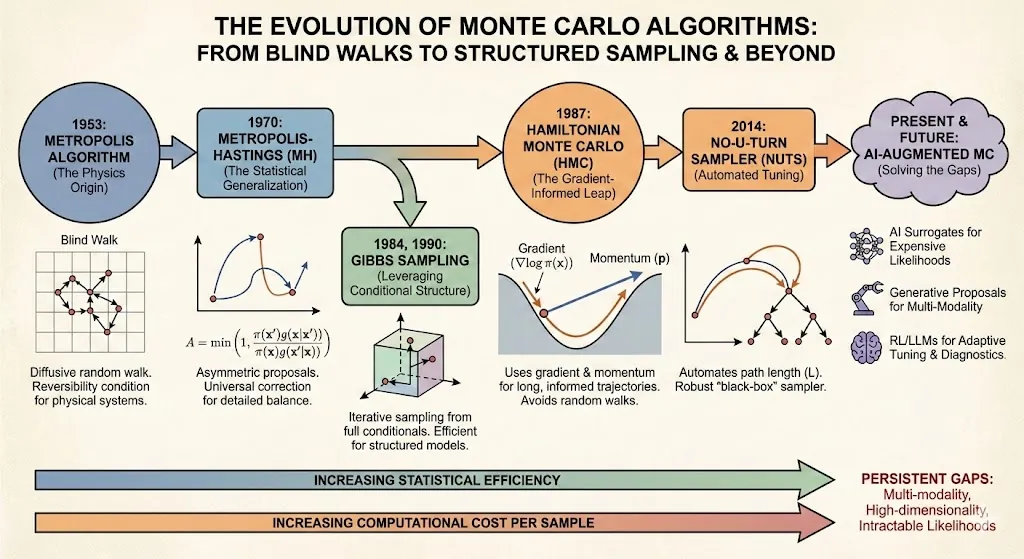
Monte Carlo algorithms are a foundational pillar of modern computational science, yet their effective application hinges on a deep understanding of their performance trade offs. This paper presents a critical analysis of the evolution of Monte Carlo algorithms, focusing on the persistent tension between statistical efficiency and computational cost. We describe the historical development from the foundational Metropolis Hastings algorithm to contemporary methods like Hamiltonian Monte Carlo. A central emphasis of this survey is the rigorous discussion of time and space complexity, including upper, lower, and asymptotic tight bounds for each major algorithm class. We examine the specific motivations for developing these methods and the key theoretical and practical observations such as the introduction of gradient information and adaptive tuning in HMC that led to successively better solutions. Furthermore, we provide a justification framework that discusses explicit situations in which using one algorithm is demonstrably superior to another for the same problem. The paper concludes by assessing the profound significance and impact of these algorithms and detailing major current research challenges.
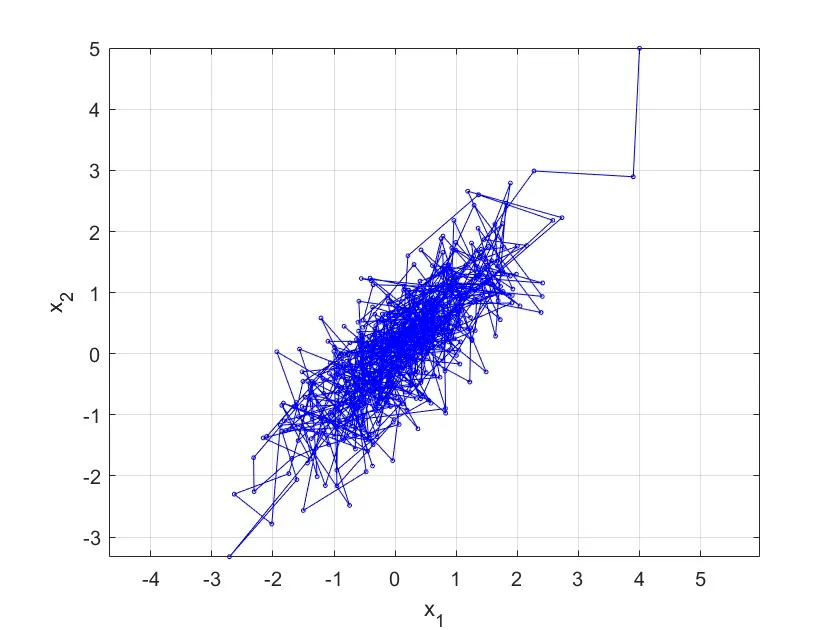
We introduce shielded Langevin Monte Carlo (LMC), a constrained sampler inspired by navigation functions, capable of sampling from unnormalized target distributions defined over punctured supports. In other words, this approach samples from non-convex spaces defined as convex sets with convex holes. This defines a novel and challenging problem in constrained sampling. To do so, the sampler incorporates a combination of a spatially adaptive temperature and a repulsive drift to ensure that samples remain within the feasible region. Experiments on a 2D Gaussian mixture and multiple-input multiple-output (MIMO) symbol detection showcase the advantages of the proposed shielded LMC in contrast to unconstrained cases.
Learning probabilistic surrogates for PDEs remains challenging in data-scarce regimes: neural operators require large amounts of high-fidelity data, while generative approaches typically sacrifice resolution invariance. We formulate flow matching in an infinite-dimensional function space to learn a probabilistic transport that maps low-fidelity approximations to the manifold of high-fidelity PDE solutions via learned residual corrections. We develop a conditional neural operator architecture based on feature-wise linear modulation for flow-matching vector fields directly in function space, enabling inference at arbitrary spatial resolutions without retraining. To improve stability and representational control of the induced neural ODE, we parameterize the flow vector field as a sum of a linear operator and a nonlinear operator, combining lightweight linear components with a conditioned Fourier neural operator for expressive, input-dependent dynamics. We then formulate a residual-augmented learning strategy where the flow model learns probabilistic corrections from inexpensive low-fidelity surrogates to high-fidelity solutions, rather than learning the full solution mapping from scratch. Finally, we derive tractable training objectives that extend conditional flow matching to the operator setting with input-function-dependent couplings. To demonstrate the effectiveness of our approach, we present numerical experiments on a range of PDEs, including the 1D advection and Burgers' equation, and a 2D Darcy flow problem for flow through a porous medium. We show that the proposed method can accurately learn solution operators across different resolutions and fidelities and produces uncertainty estimates that appropriately reflect model confidence, even when trained on limited high-fidelity data.
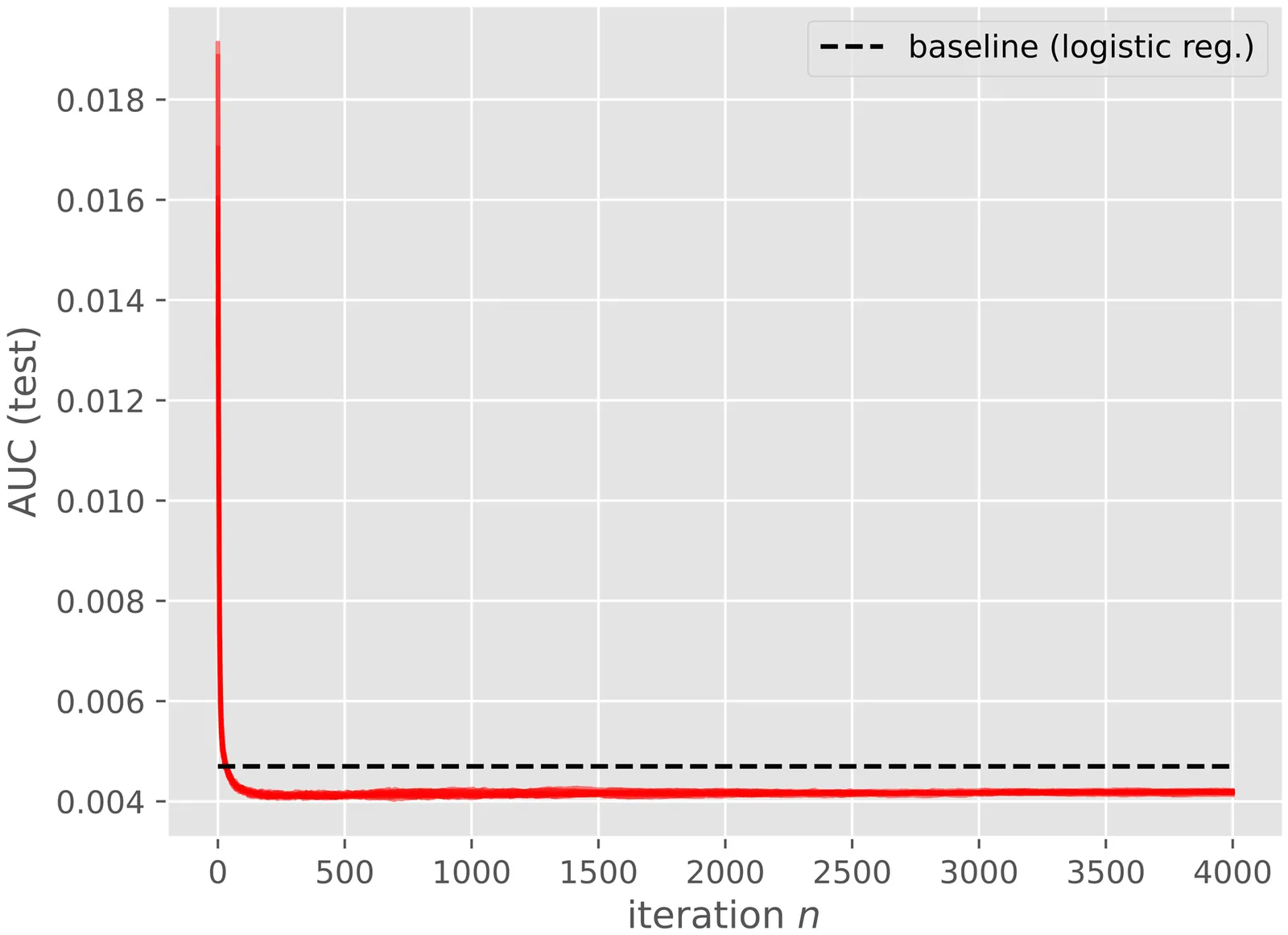
We investigate the convergence properties of a class of iterative algorithms designed to minimize a potentially non-smooth and noisy objective function, which may be algebraically intractable and whose values may be obtained as the output of a black box. The algorithms considered can be cast under the umbrella of a generalised gradient descent recursion, where the gradient is that of a smooth approximation of the objective function. The framework we develop includes as special cases model-based and mollification methods, two classical approaches to zero-th order optimisation. The convergence results are obtained under very weak assumptions on the regularity of the objective function and involve a trade-off between the degree of smoothing and size of the steps taken in the parameter updates. As expected, additional assumptions are required in the stochastic case. We illustrate the relevance of these algorithms and our convergence results through a challenging classification example from machine learning.
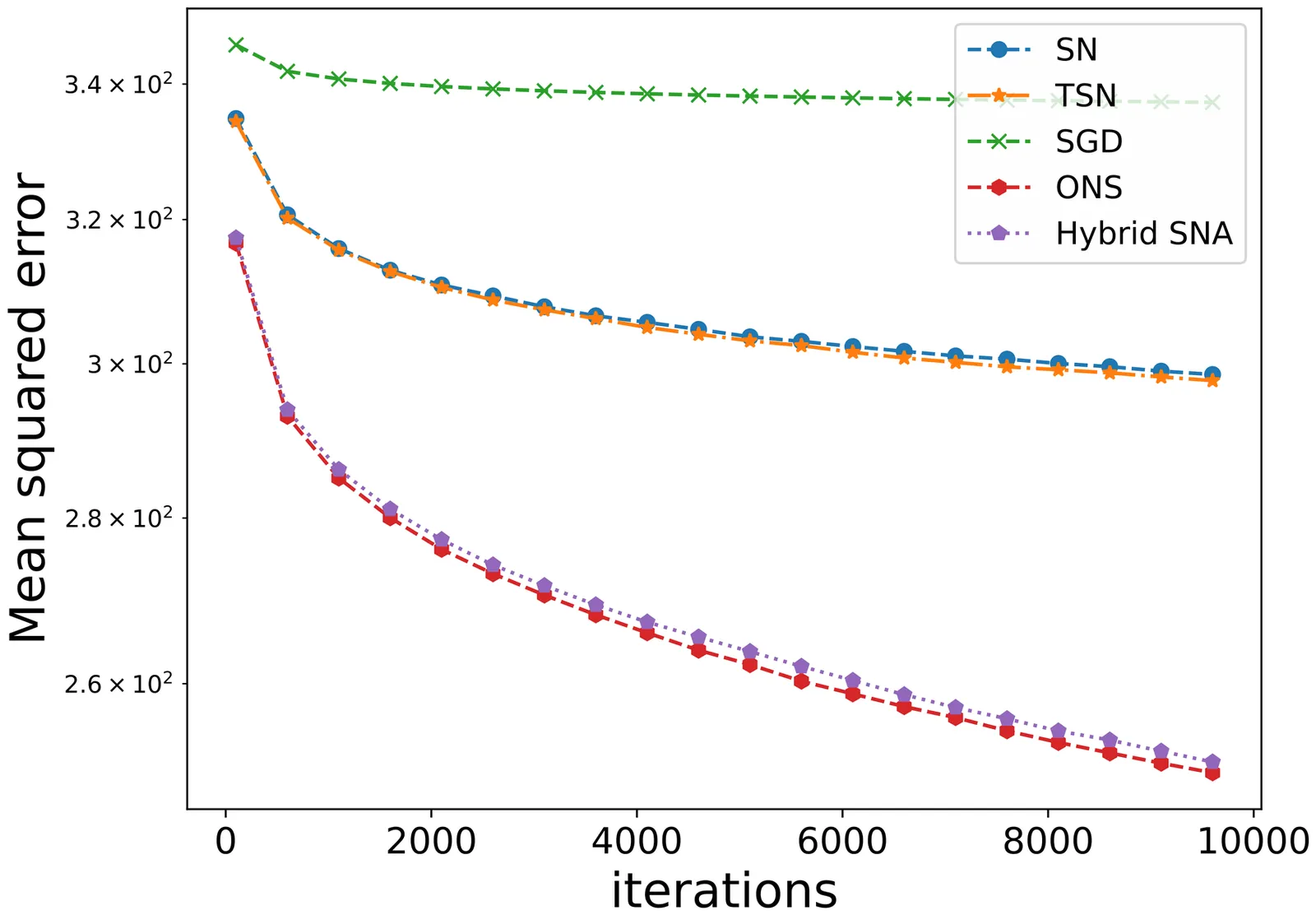
In this paper, we investigate a second-order stochastic algorithm for solving large-scale binary classification problems. We propose to make use of a new hybrid stochastic Newton algorithm that includes two weighted components in the Hessian matrix estimation: the first one coming from the natural Hessian estimate and the second associated with the stochastic gradient information. Our motivation comes from the fact that both parts evaluated at the true parameter of logistic regression, are equal to the Hessian matrix. This new formulation has several advantages and it enables us to prove the almost sure convergence of our stochastic algorithm to the true parameter. Moreover, we significantly improve the almost sure rate of convergence to the Hessian matrix. Furthermore, we establish the central limit theorem for our hybrid stochastic Newton algorithm. Finally, we show a surprising result on the almost sure convergence of the cumulative excess risk.
Iterated sampling importance resampling (i-SIR) is a Markov chain Monte Carlo (MCMC) algorithm which is based on $N$ independent proposals. As $N$ grows, its samples become nearly independent, but with an increased computational cost. We discuss a method which finds an approximately optimal number of proposals $N$ in terms of the asymptotic efficiency. The optimal $N$ depends on both the mixing properties of the i-SIR chain and the (parallel) computing costs. Our method for finding an appropriate $N$ is based on an approximate asymptotic variance of the i-SIR, which has similar properties as the i-SIR asymptotic variance, and a generalised i-SIR transition having fractional `number of proposals.' These lead to an adaptive i-SIR algorithm, which tunes the number of proposals automatically during sampling. Our experiments demonstrate that our approximate efficiency and the adaptive i-SIR algorithm have promising empirical behaviour. We also present new theoretical results regarding the i-SIR, such as the convexity of asymptotic variance in the number of proposals, which can be of independent interest.
 2511.22564
2511.22564In an earlier joint work, we studied a sequential Monte Carlo algorithm to sample from the Gibbs measure supported on torus with a non-convex energy function at a low temperature, where we proved that the time complexity of the algorithm is polynomial in the inverse temperature. However, the analysis in that torus setting relied crucially on compactness and does not directly extend to unbounded domains. This work introduces a new approach that resolves this issue and establishes a similar result for sampling from Gibbs measures supported on Rd. In particular, our main result shows that for double-well energy with equal well depths, the time complexity scales as seventh power of the inverse temperature, and quadratically in both the inverse allowed absolute error and probability error.
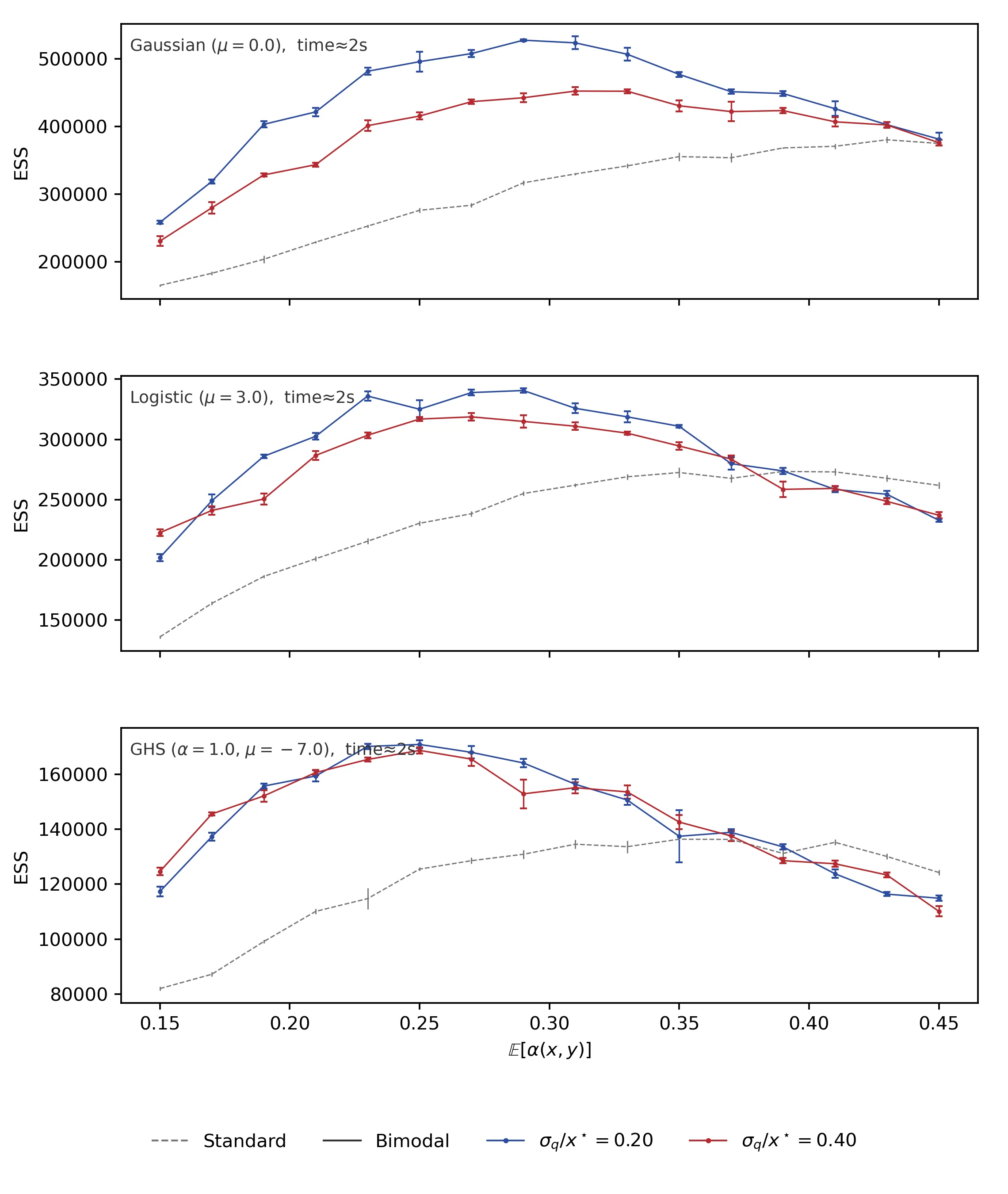
Markov Chain Monte Carlo (MCMC) is a flexible approach to approximate sampling from intractable probability distributions, with a rich theoretical foundation and comprising a wealth of exemplar algorithms. While the qualitative correctness of MCMC algorithms is often easy to ensure, their practical efficiency is contingent on the `target' distribution being reasonably well-behaved. In this work, we concern ourself with the scenario in which this good behaviour is called into question, reviewing an emerging line of work on `robust' MCMC algorithms which can perform acceptably even in the face of certain pathologies. We focus on two particular pathologies which, while simple, can already have dramatic effects on standard `local' algorithms. The first is roughness, whereby the target distribution varies so rapidly that the numerical stability of the algorithm is tenuous. The second is flatness, whereby the landscape of the target distribution is instead so barren and uninformative that one becomes lost in uninteresting parts of the state space. In each case, we formulate the pathology in concrete terms, review a range of proposed algorithmic remedies to the pathology, and outline promising directions for future research.

This paper proposes a novel Bayesian framework for solving Poisson inverse problems by devising a Monte Carlo sampling algorithm which accounts for the underlying non-Euclidean geometry. To address the challenges posed by the Poisson likelihood -- such as non-Lipschitz gradients and positivity constraints -- we derive a Bayesian model which leverages exact and asymptotically exact data augmentations. In particular, the augmented model incorporates two sets of splitting variables both derived through a Bregman divergence based on the Burg entropy. Interestingly the resulting augmented posterior distribution is characterized by conditional distributions which benefit from natural conjugacy properties and preserve the intrinsic geometry of the latent and splitting variables. This allows for efficient sampling via Gibbs steps, which can be performed explicitly for all conditionals, except the one incorporating the regularization potential. For this latter, we resort to a Hessian Riemannian Langevin Monte Carlo (HRLMC) algorithm which is well suited to handle priors with explicit or easily computable score functions. By operating on a mirror manifold, this Langevin step ensures that the sampling satisfies the positivity constraints and more accurately reflects the underlying problem structure. Performance results obtained on denoising, deblurring, and positron emission tomography (PET) experiments demonstrate that the method achieves competitive performance in terms of reconstruction quality compared to optimization- and sampling-based approaches.
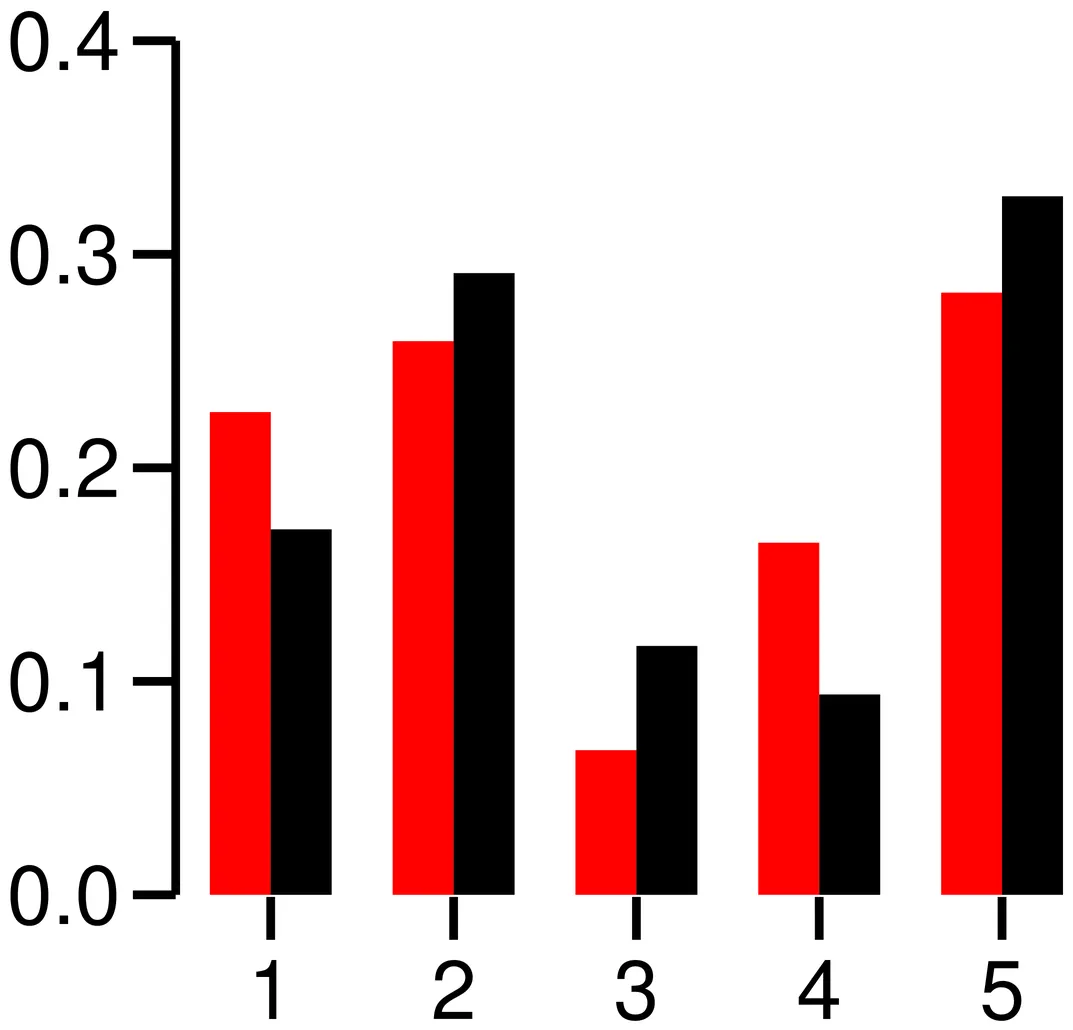
The Metropolis-Hastings algorithm has been extensively studied in the estimation and simulation literature, with most prior work focusing on convergence behavior and asymptotic theory. However, its covariance structure-an important statistical property for both theory and implementation-remains less understood. In this work, we provide new theoretical insights into the scalar case, focusing primarily on symmetric unimodal target distributions with symmetric random walk proposals, where we also establish an optimal proposal design. In addition, we derive some more general results beyond this setting. For the high-dimensional case, we relate the covariance matrix to the classical 0.23 average acceptance rate tuning criterion.
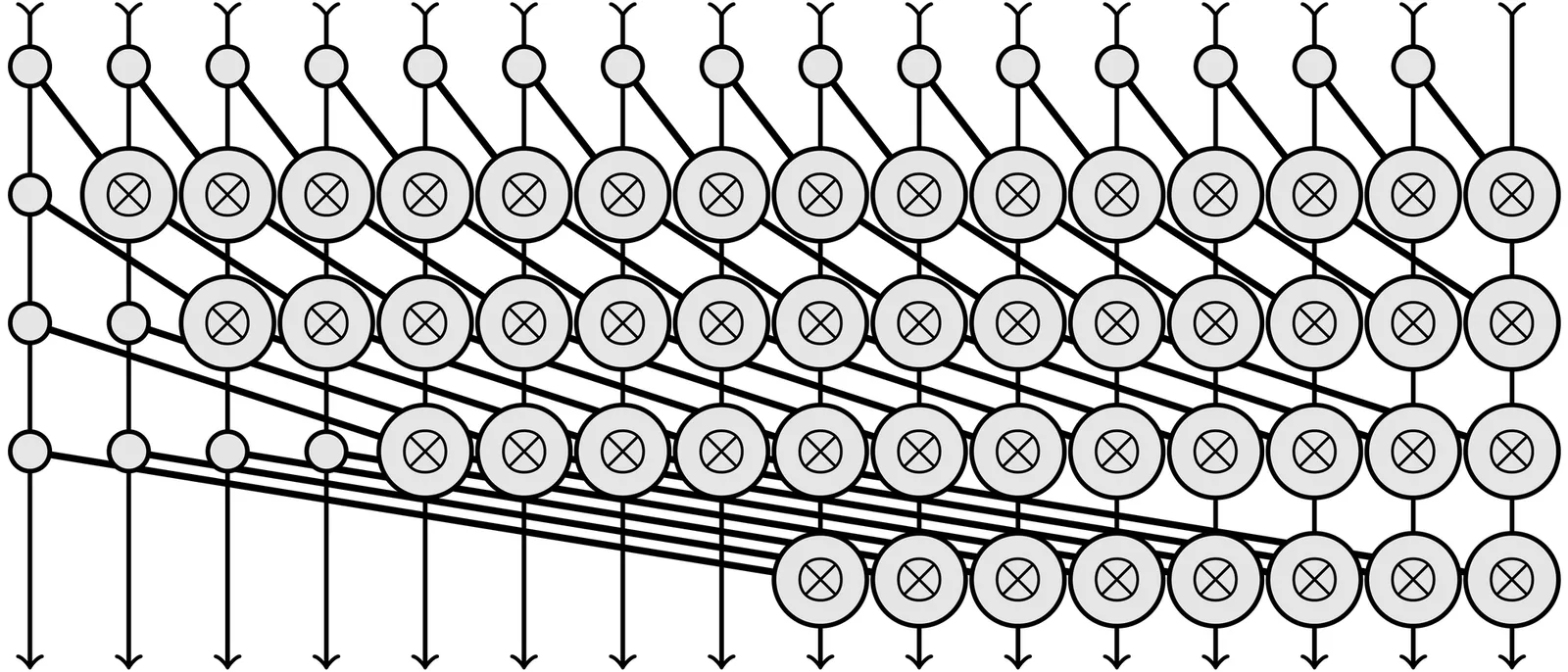
This paper presents an experimental evaluation of parallel-in-time Kalman filters and smoothers using graphics processing units (GPUs). In particular, the paper evaluates different all-prefix-sum algorithms, that is, parallel scan algorithms for temporal parallelization of Kalman filters and smoothers in two ways: by calculating the required number of operations via simulation, and by measuring the actual run time of the algorithms on real GPU hardware. In addition, a novel parallel-in-time two-filter smoother is proposed and experimentally evaluated. Julia code for Metal and CUDA implementations of all the algorithms is made publicly available.
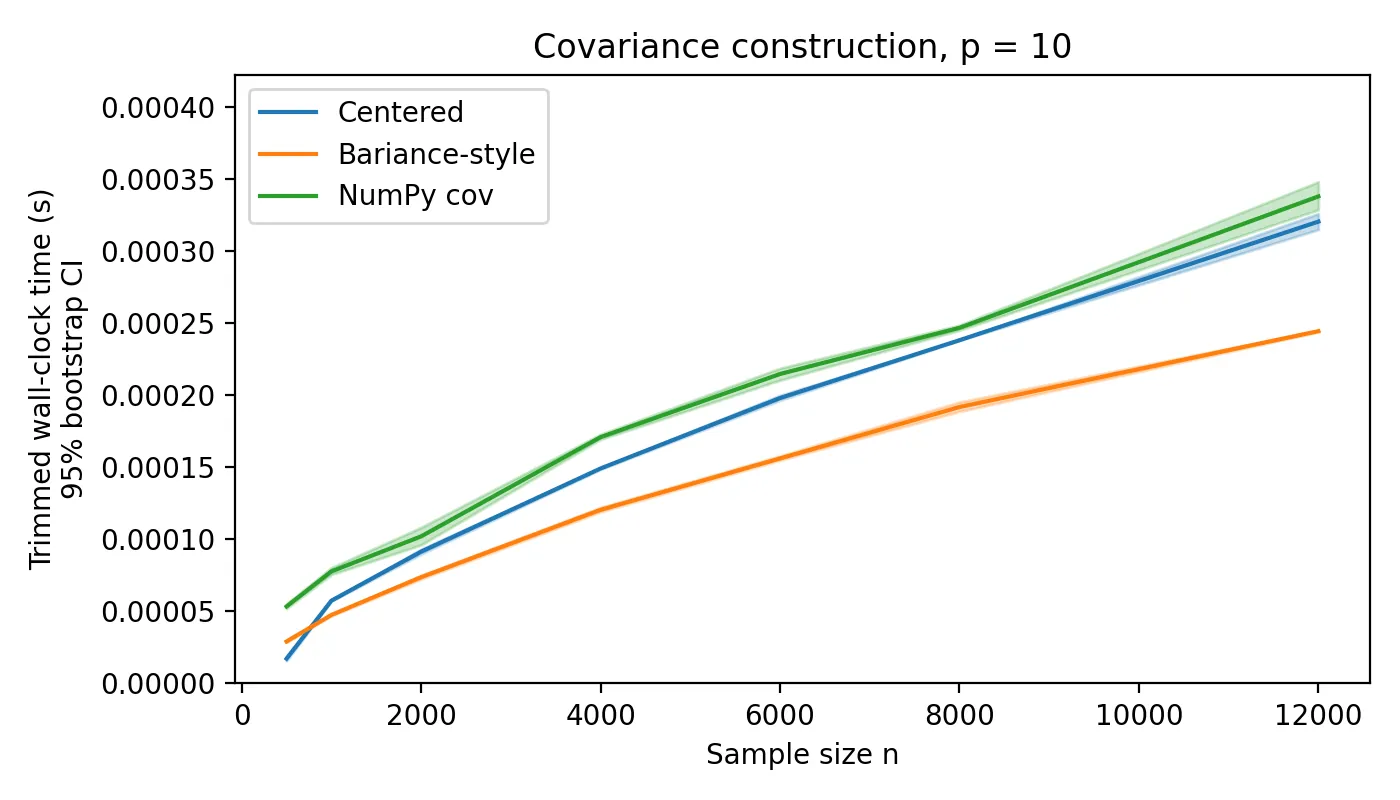
Reichel (2025) defined the bariance as a pairwise-difference measure that can be rewritten in linear time using only scalar sums. We extend this idea to the covariance matrix by showing that the standard matrix expression involving the uncentered Gram matrix and a correction term is algebraically identical to the pairwise-difference definition while avoiding explicit centering. The computation then reduces to one outer product of dimension p-by-p and a single subtraction. Benchmarks in Python show clear runtime gains, especially when BLAS optimizations are absent. Optionally faster Gram-matrix routines such as RXTX (Rybin et al., 2025) further reduce overall cost.
We present a suite of packages in R, Python, Julia, and C++ that efficiently solve the Sorted L-One Penalized Estimation (SLOPE) problem. The packages feature a highly efficient hybrid coordinate descent algorithm that fits generalized linear models (GLMs) and supports a variety of loss functions, including Gaussian, binomial, Poisson, and multinomial logistic regression. Our implementation is designed to be fast, memory-efficient, and flexible. The packages support a variety of data structures (dense, sparse, and out-of-memory matrices) and are designed to efficiently fit the full SLOPE path as well as handle cross-validation of SLOPE models, including the relaxed SLOPE. We present examples of how to use the packages and benchmarks that demonstrate the performance of the packages on both real and simulated data and show that our packages outperform existing implementations of SLOPE in terms of speed.
 2511.00708
2511.00708We study the theoretical complexity of simulated tempering for sampling from mixtures of log-concave components differing only by location shifts. The main result establishes the first polynomial-time guarantee for simulated tempering combined with the Metropolis-adjusted Langevin algorithm (MALA) with respect to the problem dimension $d$, maximum mode displacement $D$, and logarithmic accuracy $\log ε^{-1}$. The proof builds on a general state decomposition theorem for $s$-conductance, applied to an auxiliary Markov chain constructed on an augmented space. We also obtain an improved complexity estimate for simulated tempering combined with random-walk Metropolis. Our bounds assume an inverse-temperature ladder with smallest value $β_1 = O(D^{-2})$ and spacing $β_{i+1}/β_i = 1 + O( d^{-1/2} )$, both of which are shown to be asymptotically optimal up to logarithmic factors.
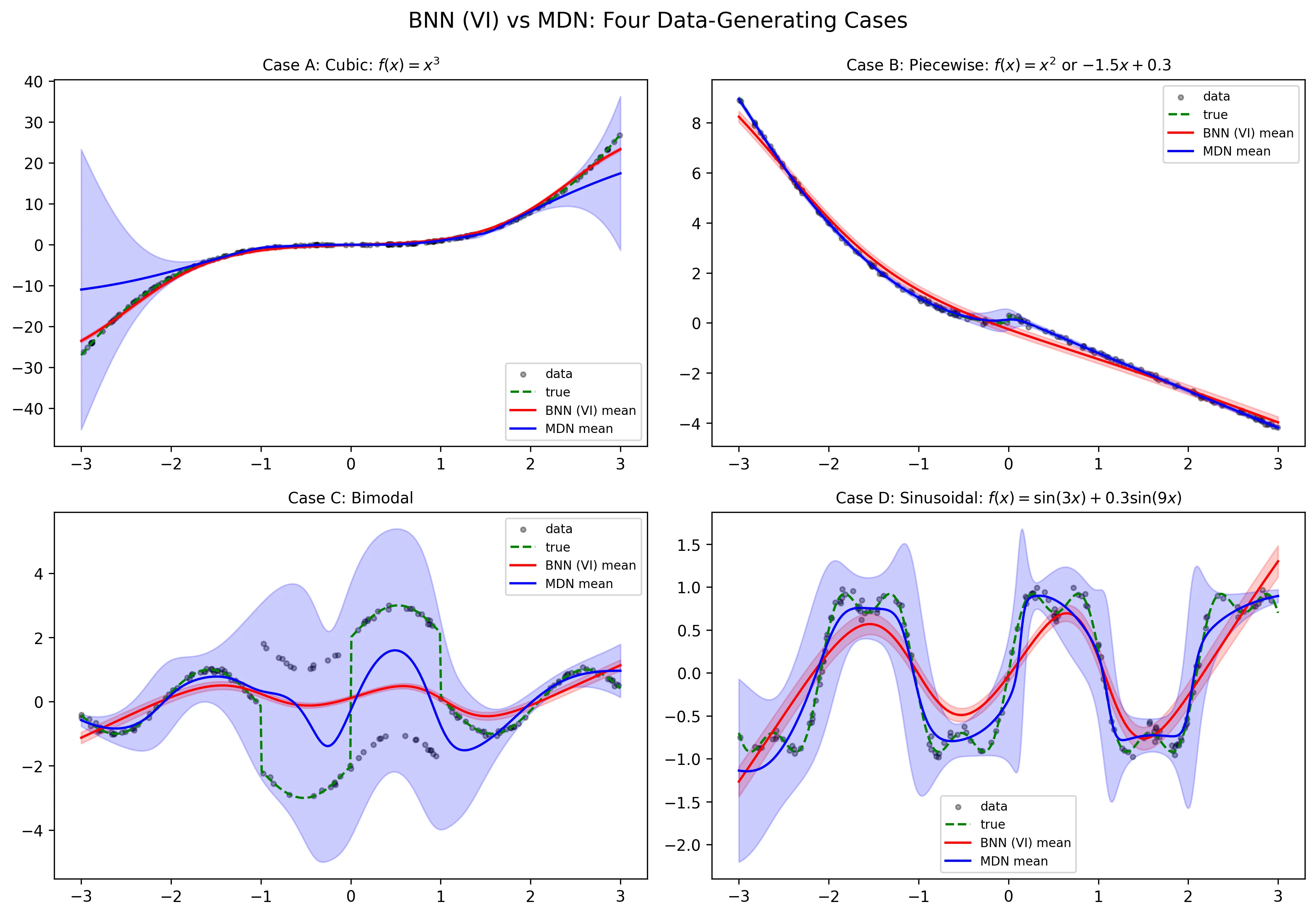
This paper investigates two prominent probabilistic neural modeling paradigms: Bayesian Neural Networks (BNNs) and Mixture Density Networks (MDNs) for uncertainty-aware nonlinear regression. While BNNs incorporate epistemic uncertainty by placing prior distributions over network parameters, MDNs directly model the conditional output distribution, thereby capturing multimodal and heteroscedastic data-generating mechanisms. We present a unified theoretical and empirical framework comparing these approaches. On the theoretical side, we derive convergence rates and error bounds under Hölder smoothness conditions, showing that MDNs achieve faster Kullback-Leibler (KL) divergence convergence due to their likelihood-based nature, whereas BNNs exhibit additional approximation bias induced by variational inference. Empirically, we evaluate both architectures on synthetic nonlinear datasets and a radiographic benchmark (RSNA Pediatric Bone Age Challenge). Quantitative and qualitative results demonstrate that MDNs more effectively capture multimodal responses and adaptive uncertainty, whereas BNNs provide more interpretable epistemic uncertainty under limited data. Our findings clarify the complementary strengths of posterior-based and likelihood-based probabilistic learning, offering guidance for uncertainty-aware modeling in nonlinear systems.
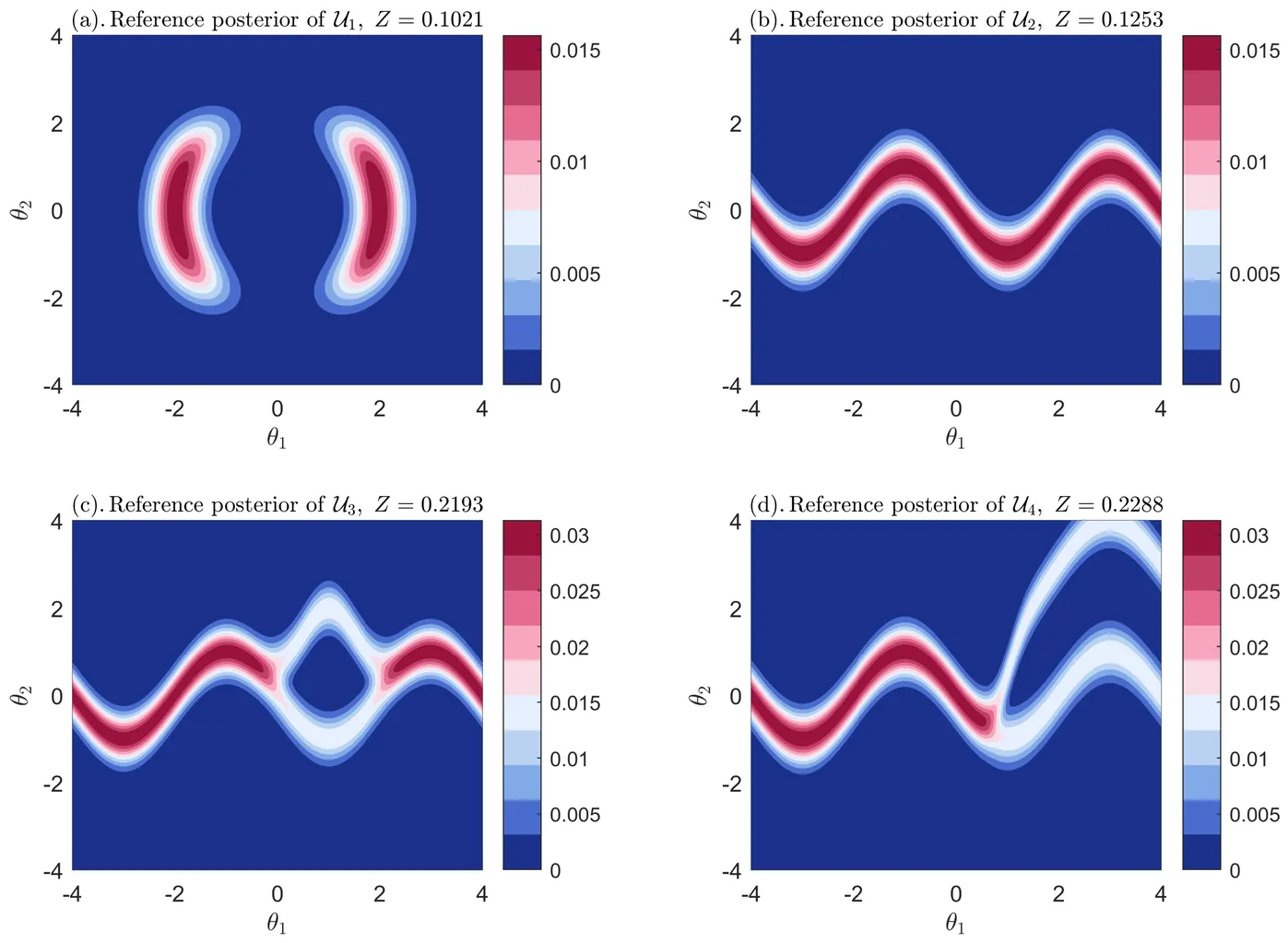
Estimating posteriors and the associated model evidences is a core issue of Bayesian model inference, and can be of great challenge given complex features of the posteriors such as multi-modalities of unequal importance, nonlinear dependencies and high sharpness. Bayesian Quadrature (BQ) has emerged as a competitive framework for tackling this challenge, as it provides flexible balance between computational cost and accuracy. The performance of a BQ scheme is fundamentally dictated by the acquisition function as it exclusively governs the generation of integration points. After reexamining one of the most advanced acquisition function from a prospective inference perspective and reformulating the quadrature rules for prediction, four new acquisition functions, inspired by distinct intuitions on expected rewards, are primarily developed, all of which are accompanied by elegant interpretations and highly efficient numerical estimators. Mathematically, these four acquisition functions measure, respectively, the prediction uncertainty of posterior, the contribution to prediction uncertainty of evidence, as well as the expected reduction of prediction uncertainties concerning posterior and evidence, and thus provide flexibility for highly effective design of integration points. These acquisition functions are further extended to the transitional BQ scheme, along with several specific refinements, to tackle the above-mentioned challenges with high efficiency and robustness. Effectiveness of the developments is ultimately demonstrated with extensive benchmark studies and application to an engineering example.
A long-standing gap exists between the theoretical analysis of Markov chain Monte Carlo convergence, which is often based on statistical divergences, and the diagnostics used in practice. We introduce the first general convergence diagnostics for Markov chain Monte Carlo based on any f-divergence, allowing users to directly monitor, among others, the Kullback--Leibler and the $χ^2$ divergences as well as the Hellinger and the total variation distances. Our first key contribution is a coupling-based `weight harmonization' scheme that produces a direct, computable, and consistent weighting of interacting Markov chains with respect to their target distribution. The second key contribution is to show how such consistent weightings of empirical measures can be used to provide upper bounds to f-divergences in general. We prove that these bounds are guaranteed to tighten over time and converge to zero as the chains approach stationarity, providing a concrete diagnostic. Numerical experiments demonstrate that our method is a practical and competitive diagnostic tool.
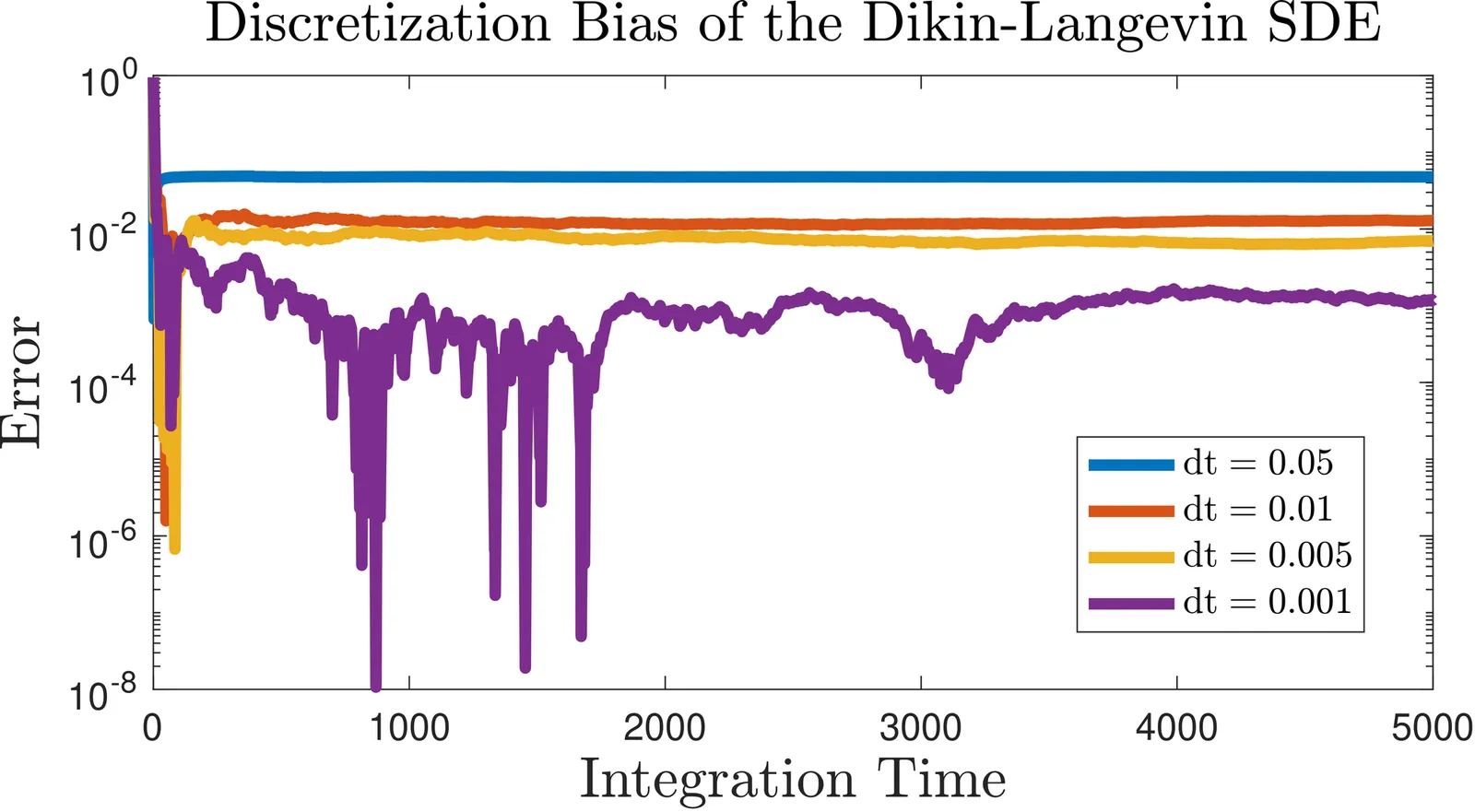
Interior-point geometry offers a straightforward approach to constrained sampling and optimization on polyhedra, eliminating reflections and ad hoc projections. We exploit the Dikin log-barrier to define a Dikin--Langevin diffusion whose drift and noise are modulated by the inverse barrier Hessian. In continuous time, we establish a boundary no-flux property; trajectories started in the interior remain in $U$ almost surely, so feasibility is maintained by construction. For computation, we adopt a discretize-then-correct design: an Euler--Maruyama proposal with state-dependent covariance, followed by a Metropolis--Hastings correction that targets the exact constrained law and reduces to a Dikin random walk when $f$ is constant. Numerically, the unadjusted diffusion exhibits the expected first-order step size bias, while the MH-adjusted variant delivers strong convergence diagnostics on anisotropic, box-constrained Gaussians (rank-normalized split-$\hat{R}$ concentrated near $1$) and higher inter-well transition counts on a bimodal target, indicating superior cross-well mobility. Taken together, these results demonstrate that coupling calibrated stochasticity with interior-point preconditioning provides a practical, reflection-free approach to sampling and optimization over polyhedral domains, offering clear advantages near faces, corners, and in nonconvex landscapes.
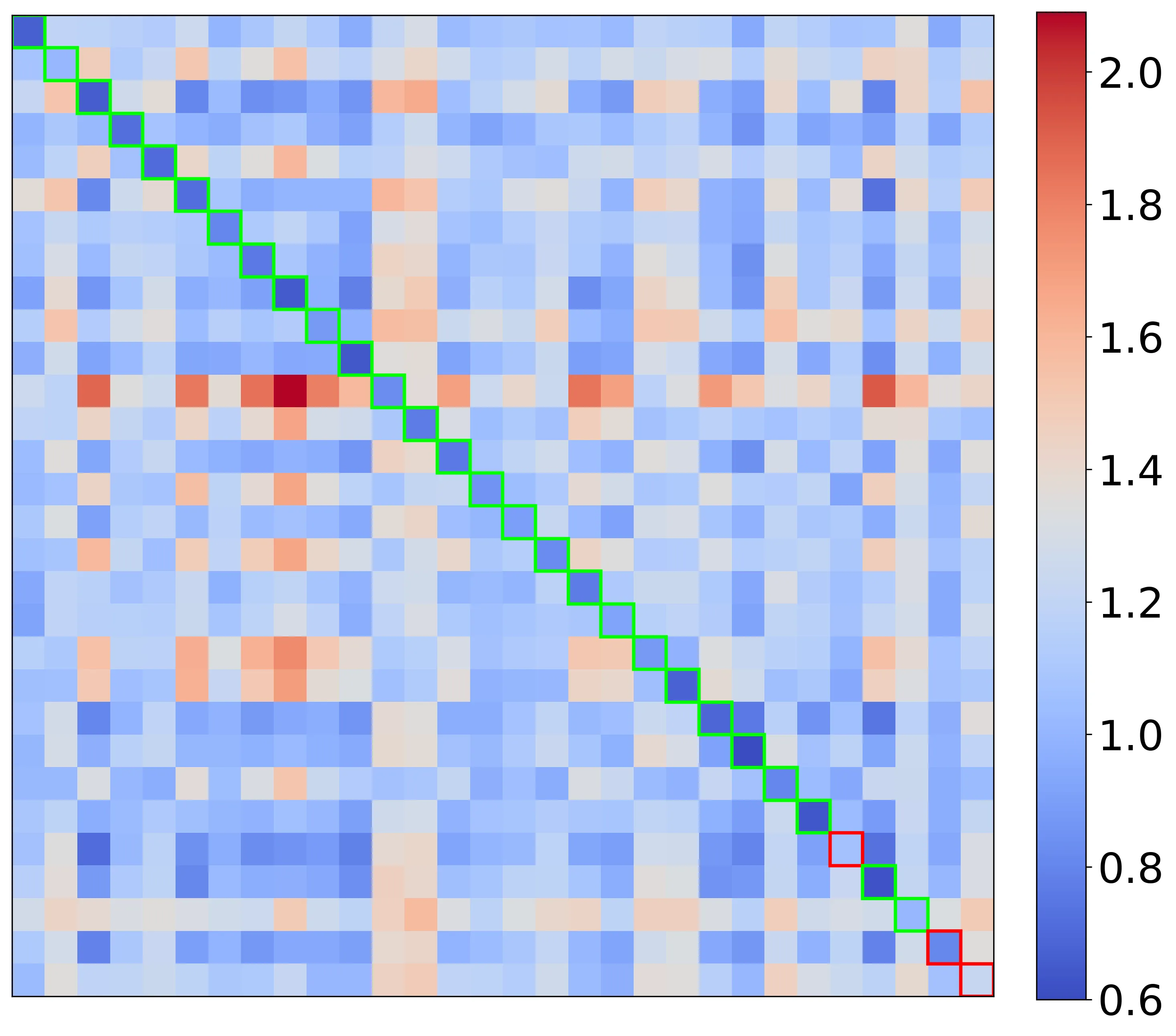
We present spd-metrics-id, a Python package for computing distances and divergences between symmetric positive-definite (SPD) matrices. Unlike traditional toolkits that focus on specific applications, spd-metrics-id provides a unified, extensible, and reproducible framework for SPD distance computation. The package supports a wide variety of geometry-aware metrics, including Alpha-z Bures-Wasserstein, Alpha-Procrustes, affine-invariant Riemannian, log-Euclidean, and others, and is accessible both via a command-line interface and a Python API. Reproducibility is ensured through Docker images and Zenodo archiving. We illustrate usage through a connectome fingerprinting example, but the package is broadly applicable to covariance analysis, diffusion tensor imaging, and other domains requiring SPD matrix comparison. The package is openly available at https://pypi.org/project/spd-metrics-id/.
Simulating the kinetic Langevin dynamics is a popular approach for sampling from distributions, where only their unnormalized densities are available. Various discretizations of the kinetic Langevin dynamics have been considered, where the resulting algorithm is collectively referred to as the kinetic Langevin Monte Carlo (KLMC) or underdamped Langevin Monte Carlo. Specifically, the stochastic exponential Euler discretization, or exponential integrator for short, has previously been studied under strongly log-concave and log-Lipschitz smooth potentials via the synchronous Wasserstein coupling strategy. Existing analyses, however, impose restrictions on the parameters that do not explain the behavior of KLMC under various choices of parameters. In particular, all known results fail to hold in the overdamped regime, suggesting that the exponential integrator degenerates in the overdamped limit. In this work, we revisit the synchronous Wasserstein coupling analysis of KLMC with the exponential integrator. Our refined analysis results in Wasserstein contractions and bounds on the asymptotic bias that hold under weaker restrictions on the parameters, which assert that the exponential integrator is capable of stably simulating the kinetic Langevin dynamics in the overdamped regime, as long as proper time acceleration is applied.