Formal Languages and Automata Theory

arXiv:cs.FL

Covers automata theory, formal language theory, grammars, and combinatorics on words.

Looking for a broader view? This category is part of:

Trending in Formal Languages and Automata Theory

Bounded treewidth, multiple context-free grammars, and downward closures

The reachability problem in multi-pushdown automata (MPDA) has many applications in static analysis of recursive programs. An example is safety verification of multi-threaded recursive programs with shared memory. Since these problems are undecidable, the literature contains many decidable (and efficient) underapproximations of MPDA. A uniform framework that captures many of these underapproximations is that of bounded treewidth (tw): To each execution of the MPDA, we associate a graph; then we consider the subset of all graphs that have a wt at most $k$, for some constant $k$. In fact, bounding tw is a generic approach to obtain classes of systems with decidable reachability, even beyond MPDA underapproximations. The resulting systems are also called MSO-definable bounded-tw systems. While bounded tw is a powerful tool for reachability and similar types of analysis, the word languages (i.e. action sequences corresponding to executions) of these systems remain far from understood. For the slight restriction of bounded special tw, or "bounded-stw" (which is equivalent to bounded tw on MPDA, and even includes all bounded-tw systems studied in the literature), this work reveals a connection with multiple context-free languages (MCFL), a concept from computational linguistics. We show that the word languages of MSO-definable bounded-stw systems are exactly the MCFL. We exploit this connection to provide an optimal algorithm for computing downward closures (dcl) for MSO-definable bounded-stw systems. Computing dcl is a notoriously difficult task that has many applications in the verification of complex systems: As an example application, we show that in programs with dynamic spawning of MSO-definable bounded-stw processes, safety verification has the same complexity as in the case of processes with sequential recursive processes.

2512.019731

Dec 2025Formal Languages and Automata Theory

Related categories:

Artificial Intelligence Hardware Architecture Computational Complexity Computational Engineering, Finance, and Science Computational Geometry

92 papers

2601.02251

Deciding Serializability in Network Systems

We present the SER modeling language for automatically verifying serializability of concurrent programs, i.e., whether every concurrent execution of the program is equivalent to some serial execution. SER programs are suitably restricted to make this problem decidable, while still allowing for an unbounded number of concurrent threads of execution, each potentially running for an unbounded number of steps. Building on prior theoretical results, we give the first automated end-to-end decision procedure that either proves serializability by producing a checkable certificate, or refutes it by producing a counterexample trace. We also present a network-system abstraction to which SER programs compile. Our decision procedure then reduces serializability in this setting to a Petri net reachability query. Furthermore, in order to scale, we curtail the search space via multiple optimizations, including Petri net slicing, semilinear-set compression, and Presburger-formula manipulation. We extensively evaluate our framework and show that, despite the theoretical hardness of the problem, it can successfully handle various models of real-world programs, including stateful firewalls, BGP routers, and more.

2601.02251Jan 2026

View

Probabilistic Programming Meets Automata Theory: Exact Inference using Weighted Automata

Probabilistic programs encode stochastic models as ordinary-looking programs with primitives for sampling numbers from predefined distributions and conditioning. Their applications include, among many others, machine learning and modeling of autonomous systems. The analysis of probabilistic programs is often quantitative - it involves reasoning about numerical properties like probabilities and expectations. A particularly important quantitative property of probabilistic programs is their posterior distribution, i.e., the distribution over possible outputs for a given input (or prior) distribution. Computing the posterior distribution exactly is known as exact inference. We present our current research using weighted automata, a generalization of the well-known finite automata, for performing exact inference in a restricted class of discrete probabilistic programs. This is achieved by encoding distributions over program variables - possibly with infinite support - as certain weighted automata. The semantics of our programming language then corresponds to common automata-theoretic constructions, such as product, concatenation, and others.

2512.13185Dec 2025

View

Uniform winning strategies for the synchronization games on subclasses of finite automata

The pseudovariety $\mathbf{DS}$ consists of all finite monoids whose regular $D$-classes form subsemigroups. We exhibit a uniform winning strategy for Synchronizer in the synchronization game on every synchronizing automaton whose transition monoid lies in $\mathbf{DS}$, and we prove that $\mathbf{DS}$ is the largest pseudovariety with this property.

2512.11007Dec 2025

View

2512.10017

Complexity of Linear Subsequences of $k$-Automatic Sequences

We construct automata with input(s) in base $k$ recognizing some basic relations and study their number of states. We also consider some basic operations on $k$-automatic sequences and discuss their state complexity. We find a relationship between subword complexity of the interior sequence $(h'(i))_{i \geq 0}$ and state complexity of the linear subsequence $(h(ni+c))_{i \geq 0}$. We resolve a recent question of Zantema and Bosma about linear subsequences of $k$-automatic sequences with input in most-significant-digit-first format. We also discuss the state complexity and runtime complexity of using a reasonable interpretation of Büchi arithmetic to actually construct some of the studied automata recognizing relations or carrying out operations on automatic sequences.

2512.10017Dec 2025

View

Weakly-unambiguous Parikh automata and their link to holonomic series

We investigate the connection between properties of formal languages and properties of their generating series, with a focus on the class of holonomic power series. We first prove a strong version of a conjecture by Castiglione and Massazza: weakly-unambiguous Parikh automata are equivalent to unambiguous two-way reversal bounded counter machines, and their multivariate generating series are holonomic. We then show that the converse is not true: we construct a language whose generating series is algebraic (thus holonomic), but which is inherently weakly-ambiguous as a Parikh automata language. Finally, we prove an effective decidability result for the inclusion problem for weakly-unambiguous Parikh automata, and provide an upper-bound on to its complexity.

2512.098239Dec 2025

View

2512.09975

Generalised Arc Consistency via the Synchronised Product of Finite Automata wrt a Constraint

Given an $m$ by $n$ matrix $V$ of domain variables $v_{i,j}$ (with $i$ from $1$ to $m$ and $j$ from $1$ to $n$), where each row $i$ must be accepted by a specified Deterministic Finite Automaton (DFA) $\mathcal{A}_i$ and each column $j$ must satisfy the same constraint $\texttt{ctr}$, we show how to use the \emph{synchronised product of DFAs wrt constraint} $\texttt{ctr}$ to obtain a Berge-acyclic decomposition ensuring Generalised Arc Consistency (GAC). Such decomposition consists of one \texttt{regular} and $n$ \texttt{table} constraints. We illustrate the effectiveness of this method by solving a hydrogen distribution problem, finding optimal solutions and proving optimality quickly.

2512.09975Dec 2025

View

Unambiguisability and Register Minimisation of Min-Plus Models

We study the unambiguisability problem for min-plus (tropical) weighted automata (WFAs), and the counter-minimisation problem for tropical Cost Register Automata (CRAs), which are expressively-equivalent to WFAs. Both problems ask whether the "amount of nondeterminism" in the model can be reduced. We show that WFA unambiguisability is decidable, thus resolving this long-standing open problem. Our proof is via reduction to WFA determinisability, which was recently shown to be decidable. On the negative side, we show that CRA counter minimisation is undecidable, even for a fixed number of registers (specifically, already for 7 registers).

2512.09484Dec 2025

View

2512.07595

Specializing anti-unification for interaction models composition via gate connections

Interaction models describe distributed systems as algebraic terms, with gates marking interaction points between local views. Composing local models into a coherent global one requires aligning these gates while respecting the algebraic laws of interaction operators. We specialize anti-unification (or generalization) via a special constant-preserving variant, which preserves designated constants while generalizing the remaining structure. We develop a dedicated rule-based procedure for computing these generalizations, prove its termination, soundness, and completeness, extend it modulo equational theories, and integrate it into a standard anti-unification framework. A prototype tool demonstrates the approach's ability to recompose global interactions from partial views.

2512.07595Dec 2025

View

2512.07476

An Analysis of Decision Problems for Relational Pattern Languages under Various Constraints

Patterns are words with terminals and variables. The language of a pattern is the set of words obtained by uniformly substituting all variables with words that contain only terminals. In their original definition, patterns only allow for multiple distinct occurrences of some variables to be related by the equality relation, represented by using the same variable multiple times. In an extended notion, called relational patterns and relational pattern languages, variables may be related by arbitrary other relations. We extend the ongoing investigation of the main decision problems for patterns (namely, the membership problem, the inclusion problem, and the equivalence problem) to relational pattern languages under a wide range of individual relations. It is shown show that - even for many much simpler or less restrictive relations - the complexity and (un)decidability characteristics of these problems do not change compared to the classical case where variables are related only by equality.

2512.07476Dec 2025

View

Soft state reduction of fuzzy automata over residuated lattices

State reduction of finite automata plays a significant role in improving efficiency in formal verification, pattern recognition, and machine learning, where automata-based models are widely used. While deterministic automata have well-defined minimization procedures, reducing states in nondeterministic fuzzy finite automata (FfAs) remains challenging, especially for FfAs over non-locally finite residuated lattices like the product and Hamacher structures. This work introduces soft state reduction, an approximate method that leverages a small threshold $\varepsilon$ possibly combined with a word length bound $k$ to balance reduction accuracy and computational feasibility. By omitting fuzzy values smaller than $\varepsilon$, the underlying residuated lattice usually becomes locally finite, making computations more tractable. We introduce and study approximate invariances, which are fuzzy relations that allow merging of almost equivalent states of an FfA up to a tolerance level $\varepsilon$ and, optionally, to words of bounded length $k$. We further present an algorithm which iteratively applies such invariances to achieve reduction while preserving approximate language equivalence. Our method effectively reduces FfAs where existing techniques fail.

2512.06832Dec 2025

View

On the Impact of the Communication Model on Realisability

Multiparty Session Types (MPST) provide a type-theoretic foundation for specifying and verifying communication protocols in distributed systems. MPST rely on the notion of global type which specifies the global behaviour and local types, which are the projections of the global behaviour onto each local participant. A central notion in MPST is realisability - whether local implementations derived from a global specification correctly realise the intended protocol under a given communication model. While realisability has been extensively studied under peer-to-peer semantics, it remains poorly understood in alternative communication models such as bag-based, causally ordered, or synchronous communications. In this paper, we develop a unified framework for reasoning about realisability and subtyping across a spectrum of communication models. We show that the communication model does not impact the notion of subtyping, but that it impacts the notion of realisability. We introduce several decision procedures for subtyping checking and realisability checking with complexities ranging from NLOGSPACE to EXPSPACE depending on the assumptions made on the global types, in particular depending on their complementability and the size of a given complement.

2512.05609Dec 2025

View

Symbolic ω-automata with obligations

Extensions of ω-automata to infinite alphabets typically rely on symbolic guards to keep the transition relation finite, and on registers or memory cells to preserve information from past symbols. Symbolic transitions alone are ill-suited to act on this information, and register automata have intricate formal semantics and issues with tractability. We propose a slightly different approach based on obligations, i.e., assignment-like constructs attached to transitions. Whenever a transition with an obligation is taken, the obligation is evaluated against the current symbol and yields a constraint on the next symbol that the automaton will read. We formalize obligation automata with existential and universal branching and Emerson-Lei acceptance conditions, which subsume classic families such as Büchi, Rabin, Strett, and parity automata. We show that these automata recognise a strict superset of ω-regular languages. To illustrate the practicality of our proposal, we also introduce a machine-readable format to express obligation automata and describe a tool implementing several operations over them, including automata product and emptiness checking.

2512.02873Dec 2025

View

Bounded treewidth, multiple context-free grammars, and downward closures

2512.019731Dec 2025

View

Tahr: The Generative Attribute Grammar Framework

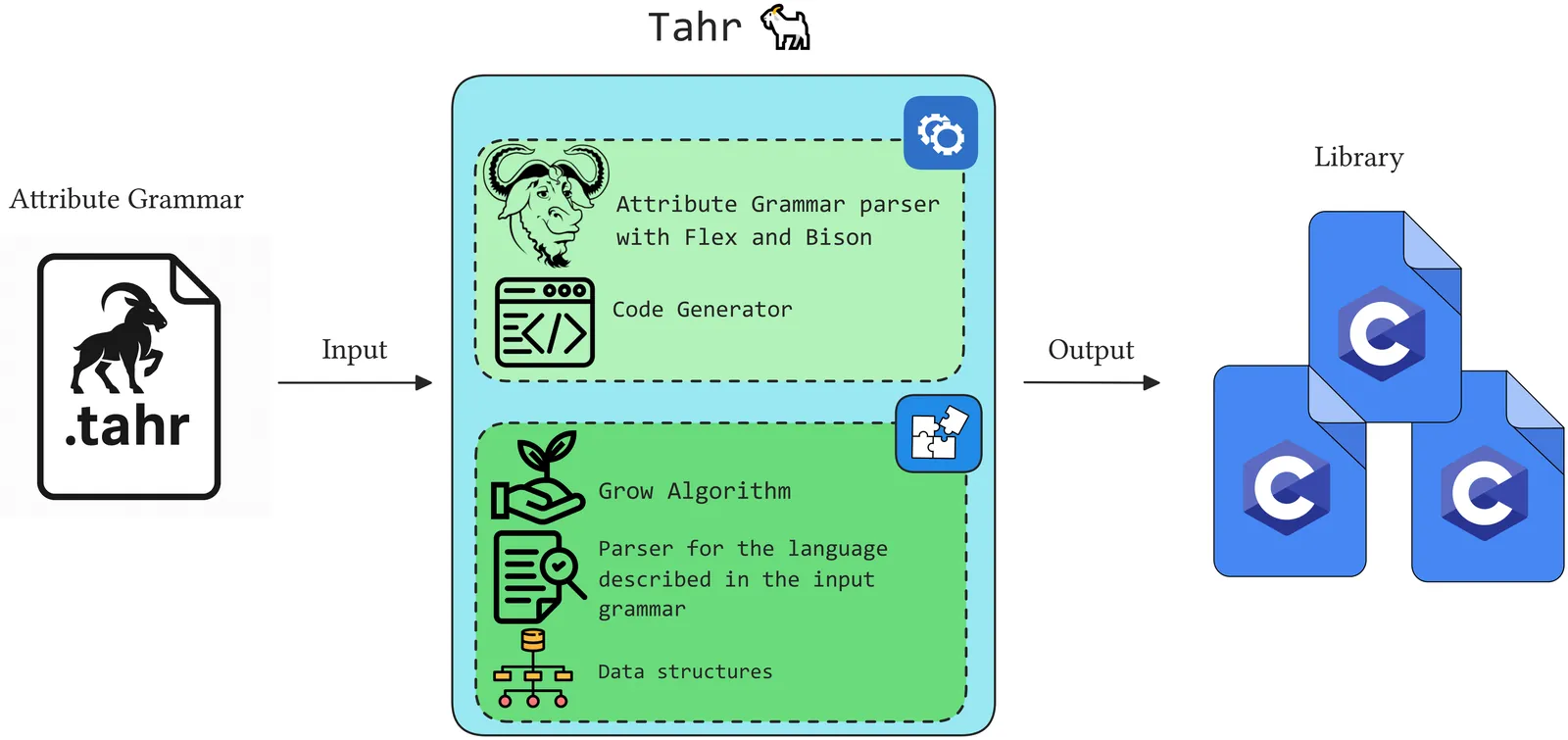
In this article, we present Tahr, a framework that allows taking attribute grammar specifications and generating a set of software artefacts that can be used programmatically to operate on text compliant with the grammars. Tahr can be used as an algorithmic workbench to test different manipulations of attribute grammars and support translation between different languages out of the box. We describe the framework's organisation, how the user can specify an attribute grammar, and the generated software artefacts. We also discuss how Tahr deals with ambiguous grammar specifications, and how this ambiguity can be effectively exploited when using attribute grammars for text generation. We test the correctness of Tahr by showing the practical possibility of translating MIPS programs into their corresponding equivalents for x86 architectures and a custom virtual machine.

2512.01872Dec 2025

View

Counting and Sampling Traces in Regular Languages

In this work, we study the problems of counting and sampling Mazurkiewicz traces that a regular language touches. Fix an alphabet $Σ$ and an independence relation $\mathbb{I} \subseteq Σ\times Σ$. The input consists of a regular language $L \subseteq Σ^*$, given by a finite automaton with $m$ states, and a natural number $n$ (in unary). For the counting problem, the goal is to compute the number of Mazurkiewicz traces (induced by $\mathbb{I}$) that intersect the $n^\text{th}$ slice $L_n = L \cap Σ^n$, i.e., traces that admit at least one linearization in $L_n$. For the sampling problem, the goal is to output a trace drawn from a distribution that is approximately uniform over all such traces. These tasks are motivated by bounded model checking with partial-order reduction, where an \emph{a priori} estimate of the reduced state space is valuable, and by testing methods for concurrent programs that use partial-order-aware random exploration. We first show that the counting problem is #P-hard even when $L$ is accepted by a deterministic automaton, in sharp contrast to counting words of a DFA, which is polynomial-time solvable. We then prove that the problem lies in #P for both NFAs and DFAs, irrespective of whether $L$ is trace-closed. Our main algorithmic contributions are a \emph{fully polynomial-time randomized approximation scheme} (FPRAS) that, with high probability, approximates the desired count within a prescribed accuracy, and a \emph{fully polynomial-time almost uniform sampler} (FPAUS) that generates traces whose distribution is provably close to uniform.

2512.00314Nov 2025

View

2512.00297

Unconditional Time and Space Complexity Lower Bounds for Intersection Non-Emptiness

We reinvestigate known lower bounds for the Intersection Non-Emptiness Problem for Deterministic Finite Automata (DFA's). We first strengthen conditional time complexity lower bounds from T. Kasai and S. Iwata (1985) which showed that Intersection Non-Emptiness is not solvable more efficiently unless there exist more efficient algorithms for non-deterministic logarithmic space ($\texttt{NL}$). Next, we apply a recent breakthrough from R. Williams (2025) on the space efficient simulation of deterministic time to show an unconditional $Ω(\frac{n^2}{\log^3(n) \log\log^2(n)})$ time complexity lower bound for Intersection Non-Emptiness. Finally, we consider implications that would follow if Intersection Non-Emptiness for a fixed number of DFA's is computationally hard for a fixed polynomial time complexity class. These implications include $\texttt{PTIME} \subseteq \texttt{DSPACE}(n^c)$ for some $c \in \mathbb{N}$ and $\texttt{PSPACE} = \texttt{EXPTIME}$.

2512.00297Nov 2025

View

The Target Discounted-Sum Problem

The target discounted-sum problem is the following: Given a rational discount factor $0<λ<1$ and three rational values $a,b$, and $t$, does there exist a finite or an infinite sequence $w \in \{a,b\}^*$ or $w \in \{a,b\}^ω$, such that $\sum_{i=0}^{|w|} w(i) λ^i$ equals $t$? The problem turns out to relate to many fields of mathematics and computer science, and its decidability question is surprisingly hard to solve. We solve the finite version of the problem, and show the hardness of the infinite version, linking it to various areas and open problems in mathematics and computer science: $β$-expansions, discounted-sum automata, piecewise affine maps, and generalizations of the Cantor set. We provide some partial results to the infinite version, among which are solutions to its restriction to eventually-periodic sequences and to the cases that $λ\geq \frac{1}{2}$ or $λ=\frac{1}{n}$, for every $n\in \mathbb{N}$. We use our results for solving some open problems on discounted-sum automata, among which are the exact-value, universality and inclusion problems for functional automata.

2511.2297925Nov 2025

View

Extended branching Rauzy induction

Branching Rauzy induction is a two-sided form of Rauzy induction that acts on regular interval exchange transformations (IETs). We introduce an extended form of branching Rauzy induction that applies to arbitrary standard IETs, including non-minimal ones. The procedure generalizes the branching Rauzy method with two induction steps, merging and splitting, to handle equal-length cuts and invariant components respectively. As an application, we show, via a stepwise morphic argument, that all return words in the language of an arbitrary IET cluster in the Burrows-Wheeler sense.

2511.22588Nov 2025

View

Softmax Transformers are Turing-Complete

Hard attention Chain-of-Thought (CoT) transformers are known to be Turing-complete. However, it is an open problem whether softmax attention Chain-of-Thought (CoT) transformers are Turing-complete. In this paper, we prove a stronger result that length-generalizable softmax CoT transformers are Turing-complete. More precisely, our Turing-completeness proof goes via the CoT extension of the Counting RASP (C-RASP), which correspond to softmax CoT transformers that admit length generalization. We prove Turing-completeness for CoT C-RASP with causal masking over a unary alphabet (more generally, for letter-bounded languages). While we show this is not Turing-complete for arbitrary languages, we prove that its extension with relative positional encoding is Turing-complete for arbitrary languages. We empirically validate our theory by training transformers for languages requiring complex (non-linear) arithmetic reasoning.

2511.20038Nov 2025

View

Notes on Stack Machines and Quantum Stack Machines

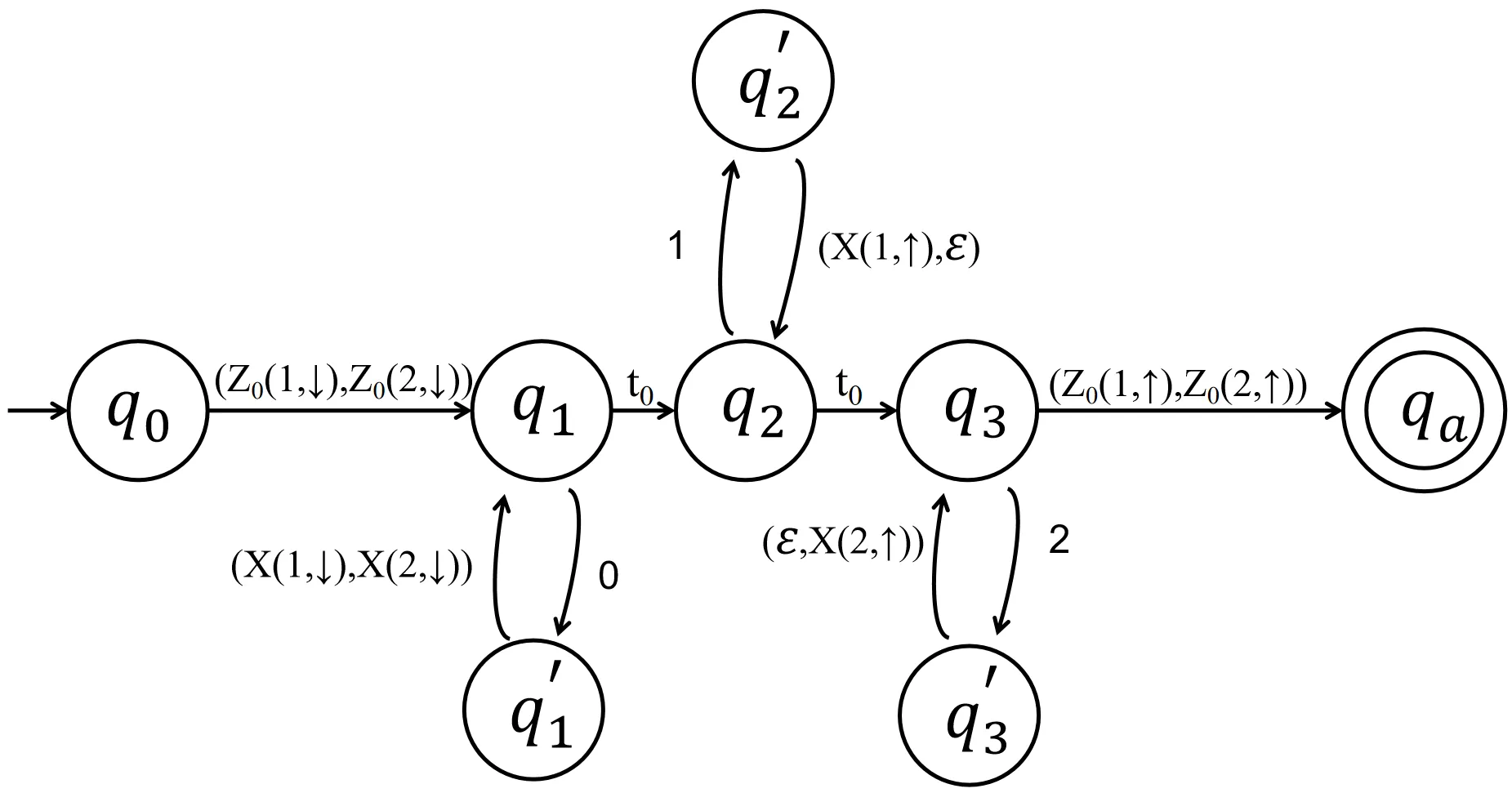
Multi-stack machines and Turing machines can simulate to each other. In this note, we give a succinct definition of multi-stack machines, and from this definition it is clearly seen that pushdown automata and deterministic finite automata are special cases of multi-stack machines. Also, with this mode of definition, pushdown automata and deterministic pushdown automata are equivalent and recognize all context-free languages. In addition, we are motivated to formulate concise definitions of quantum pushdown automata and quantum stack machines.

2511.17264Nov 2025

View

Page 1 of 5