Computational Geometry
arXiv:cs.CG
Roughly includes material in ACM Subject Classes I.3.5 and F.2.2.
Looking for a broader view? This category is part of:
135 papers
Generating Diverse TSP Tours via a Combination of Graph Pointer Network and Dispersion
We address the Diverse Traveling Salesman Problem (D-TSP), a bi-criteria optimization challenge that seeks a set of $k$ distinct TSP tours. The objective requires every selected tour to have a length at most $c|T^*|$ (where $|T^*|$ is the optimal tour length) while minimizing the average Jaccard similarity across all tour pairs. This formulation is crucial for applications requiring both high solution quality and fault tolerance, such as logistics planning, robotics pathfinding or strategic patrolling. Current methods are limited: traditional heuristics, such as the Niching Memetic Algorithm (NMA) or bi-criteria optimization, incur high computational complexity $O(n^3)$, while modern neural approaches (e.g., RF-MA3S) achieve limited diversity quality and rely on complex, external mechanisms. To overcome these limitations, we propose a novel hybrid framework that decomposes D-TSP into two efficient steps. First, we utilize a simple Graph Pointer Network (GPN), augmented with an approximated sequence entropy loss, to efficiently sample a large, diverse pool of high-quality tours. This simple modification effectively controls the quality-diversity trade-off without complex external mechanisms. Second, we apply a greedy algorithm that yields a 2-approximation for the dispersion problem to select the final $k$ maximally diverse tours from the generated pool. Our results demonstrate state-of-the-art performance. On the Berlin instance, our model achieves an average Jaccard index of $0.015$, significantly outperforming NMA ($0.081$) and RF-MA3S. By leveraging GPU acceleration, our GPN structure achieves a near-linear empirical runtime growth of $O(n)$. While maintaining solution diversity comparable to complex bi-criteria algorithms, our approach is over 360 times faster on large-scale instances (783 cities), delivering high-quality TSP solutions with unprecedented efficiency and simplicity.
2601.01132Jan 2026
View
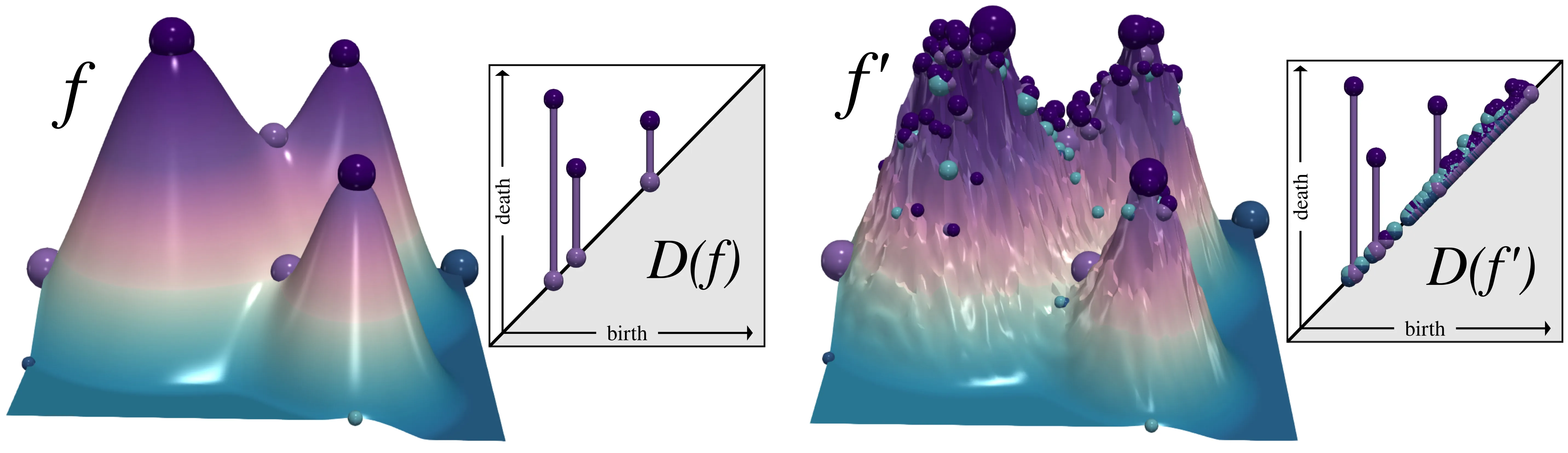
2512.20325Top-K Exterior Power Persistent Homology: Algorithm, Structure, and Stability
Exterior powers play important roles in persistent homology in computational geometry. In the present paper we study the problem of extracting the $K$ longest intervals of the exterior-power layers of a tame persistence module. We prove a structural decomposition theorem that organizes the exterior-power layers into monotone per-anchor streams with explicit multiplicities, enabling a best-first algorithm. We also show that the Top-$K$ length vector is $2$-Lipschitz under bottleneck perturbations of the input barcode, and prove a comparison-model lower bound. Our experiments confirm the theory, showing speedups over full enumeration in high overlap cases. By enabling efficient extraction of the most prominent features, our approach makes higher-order persistence feasible for large datasets and thus broadly applicable to machine learning, data science, and scientific computing.
2512.20325Dec 2025
View2512.20311Algorithm for Interpretable Graph Features via Motivic Persistent Cohomology
We present the Chromatic Persistence Algorithm (CPA), an event-driven method for computing persistent cohomological features of weighted graphs via graphic arrangements, a classical object in computational geometry. We establish rigorous complexity results: CPA is exponential in the worst case, fixed-parameter tractable in treewidth, and nearly linear for common graph families such as trees, cycles, and series-parallel graphs. Finally, we demonstrate its practical applicability through a controlled experiment on molecular-like graph structures.
2512.20311Dec 2025
View
Online Competitive Searching for Rays in the Half-plane
We consider the problem of searching for rays (or lines) in the half-plane. The given problem turns out to be a very natural extension of the cow-path problem that is lifted into the half-plane and the problem can also directly be motivated by a 1.5-dimensional terrain search problem. We present and analyse an efficient strategy for our setting and guarantee a competitive ratio of less than 9.12725 in the worst case and also prove a lower bound of at least 9.06357 for any strategy. Thus the given strategy is almost optimal, the gap is less than 0.06368. By appropriate adjustments for the terrain search problem we can improve on former results and present geometrically motivated proof arguments. As expected, the terrain itself can only be helpful for the searcher that competes against the unknown shortest path. We somehow extract the core of the problem.
2512.16622Dec 2025
View
Locally Correct Interleavings between Merge Trees
Temporal sequences of terrains arise in various application areas. To analyze them efficiently, one generally needs a suitable abstraction of the data as well as a method to compare and match them over time. In this paper we consider merge trees as a topological descriptor for terrains and the interleaving distance as a method to match and compare them. An interleaving between two merge trees consists of two maps, one in each direction. These maps must satisfy ancestor relations and hence introduce a ''shift'' between points and their image. An optimal interleaving minimizes the maximum shift; the interleaving distance is the value of this shift. However, to study the evolution of merge trees over time, we need not only a number but also a meaningful matching between the two trees. The two maps of an optimal interleaving induce a matching, but due to the bottleneck nature of the interleaving distance, this matching fails to capture local similarities between the trees. In this paper we hence propose a notion of local optimality for interleavings. To do so, we define the residual interleaving distance, a generalization of the interleaving distance that allows additional constraints on the maps. This allows us to define locally correct interleavings, which use a range of shifts across the two merge trees that reflect the local similarity well. We give a constructive proof that a locally correct interleaving always exists.
2512.16474Dec 2025
View
Hierarchical Neural Surfaces for 3D Mesh Compression
Implicit Neural Representations (INRs) have been demonstrated to achieve state-of-the-art compression of a broad range of modalities such as images, videos, 3D surfaces, and audio. Most studies have focused on building neural counterparts of traditional implicit representations of 3D geometries, such as signed distance functions. However, the triangle mesh-based representation of geometry remains the most widely used representation in the industry, while building INRs capable of generating them has been sparsely studied. In this paper, we present a method for building compact INRs of zero-genus 3D manifolds. Our method relies on creating a spherical parameterization of a given 3D mesh - mapping the surface of a mesh to that of a unit sphere - then constructing an INR that encodes the displacement vector field defined continuously on its surface that regenerates the original shape. The compactness of our representation can be attributed to its hierarchical structure, wherein it first recovers the coarse structure of the encoded surface before adding high-frequency details to it. Once the INR is computed, 3D meshes of arbitrary resolution/connectivity can be decoded from it. The decoding can be performed in real time while achieving a state-of-the-art trade-off between reconstruction quality and the size of the compressed representations.
2512.15985Dec 2025
View
Edge-wise Topological Divergence Gaps: Guiding Search in Combinatorial Optimization
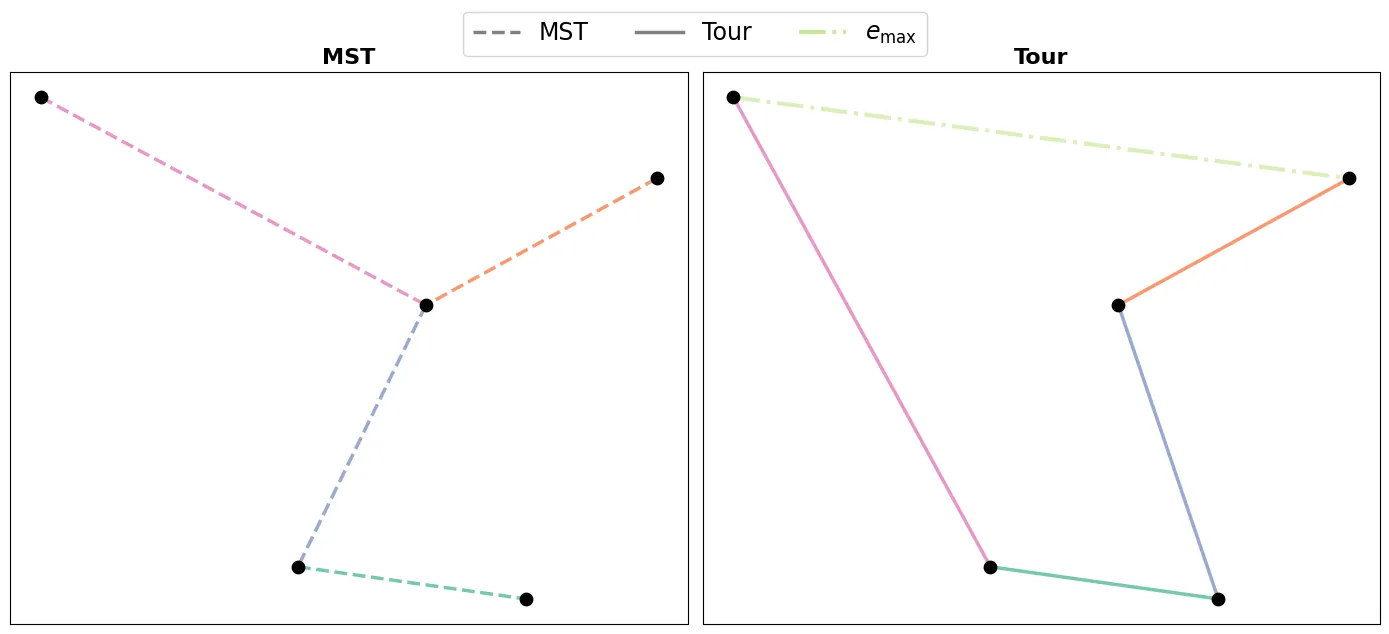
We introduce a topological feedback mechanism for the Travelling Salesman Problem (TSP) by analyzing the divergence between a tour and the minimum spanning tree (MST). Our key contribution is a canonical decomposition theorem that expresses the tour-MST gap as edge-wise topology-divergence gaps from the RTD-Lite barcode. Based on this, we develop a topological guidance for 2-opt and 3-opt heuristics that increases their performance. We carry out experiments with fine-optimization of tours obtained from heatmap-based methods, TSPLIB, and random instances. Experiments demonstrate the topology-guided optimization results in better performance and faster convergence in many cases.
2512.15800Dec 2025
View
Element-Saving Hexahedral 3-Refinement Templates
Conforming hexahedral (hex) meshes are favored in simulation for their superior numerical properties, yet automatically decomposing a general 3D volume into a conforming hex mesh remains a formidable challenge. Among existing approaches, methods that construct an adaptive Cartesian grid and subsequently convert it into a conforming mesh stand out for their robustness. However, the topological schemes enabling this conversion require strict compatibility conditions among grid elements, which inevitably refine the initial grid and increase element count. Developing more relaxed conditions to minimize this overhead has been a persistent research focus. State-of-the-art 2-refinement octree methods employ a weakly-balanced condition combined with a generalized pairing condition, using a dual transformation to yield exceptionally low element counts. Yet this approach suffers from critical limitations: information stored on primal cells, such as signed distance fields or triangle index sets, is lost after dualization, and the resulting dual cells often exhibit poor minimum scaled Jacobian (min SJ) with non-planar quadrilateral (quad) faces. Alternatively, 3-refinement 27-tree methods can directly generate conforming hex meshes through template-based replacement of primal cells, producing higher-quality elements with planar quad faces. However, previous 3-refinement techniques impose conditions far more strict than 2-refinement counterparts, severely over-refining grids by factors of ten to one hundred, creating a major bottleneck in simulation pipelines. This article introduces a novel 3-refinement approach that transforms an adaptive 3-refinement grid into a conforming grid using a moderately-balanced condition, slightly stronger than the weakly-balanced condition but substantially more relaxed than prior 3-refinement requirements...... (check PDF for the full abstract)
2512.14862Dec 2025
View
Solving the Heilbronn Triangle Problem using Global Optimization Methods
We study the Heilbronn triangle problem, which involves placing n points in the unit square such that the minimum area of any triangle formed by these points is maximized. A straightforward maximin formulation of this problem is highly non-linear and non-convex due to the existence of bilinear terms and absolute value equations. We propose two mixed-integer quadratically constrained programming (MIQCP) and one QCP formulation, which can be readily solved by any global optimization solver. We develop several formulation enhancements in the form of bound tightening and symmetry breaking inequalities that are prevalent in the global optimization literature in addition to other enhancements that exploit the problem structure. With the help of these enhancements, our models reproduce proven optimal values for instances up to n = 8 points with certified optimality in the order of seconds. In the case of n = 9 points, for which no analytical proof is known, we establish a certified optimal value by a computational effort of one day. This is a significant improvement over the previous benchmark established in 31 days of computations by Chen et al. (2017).
2512.14505Dec 2025
View
Polygon Containment and Translational Min-Hausdorff-Distance between Segment Sets are 3SUM-Hard
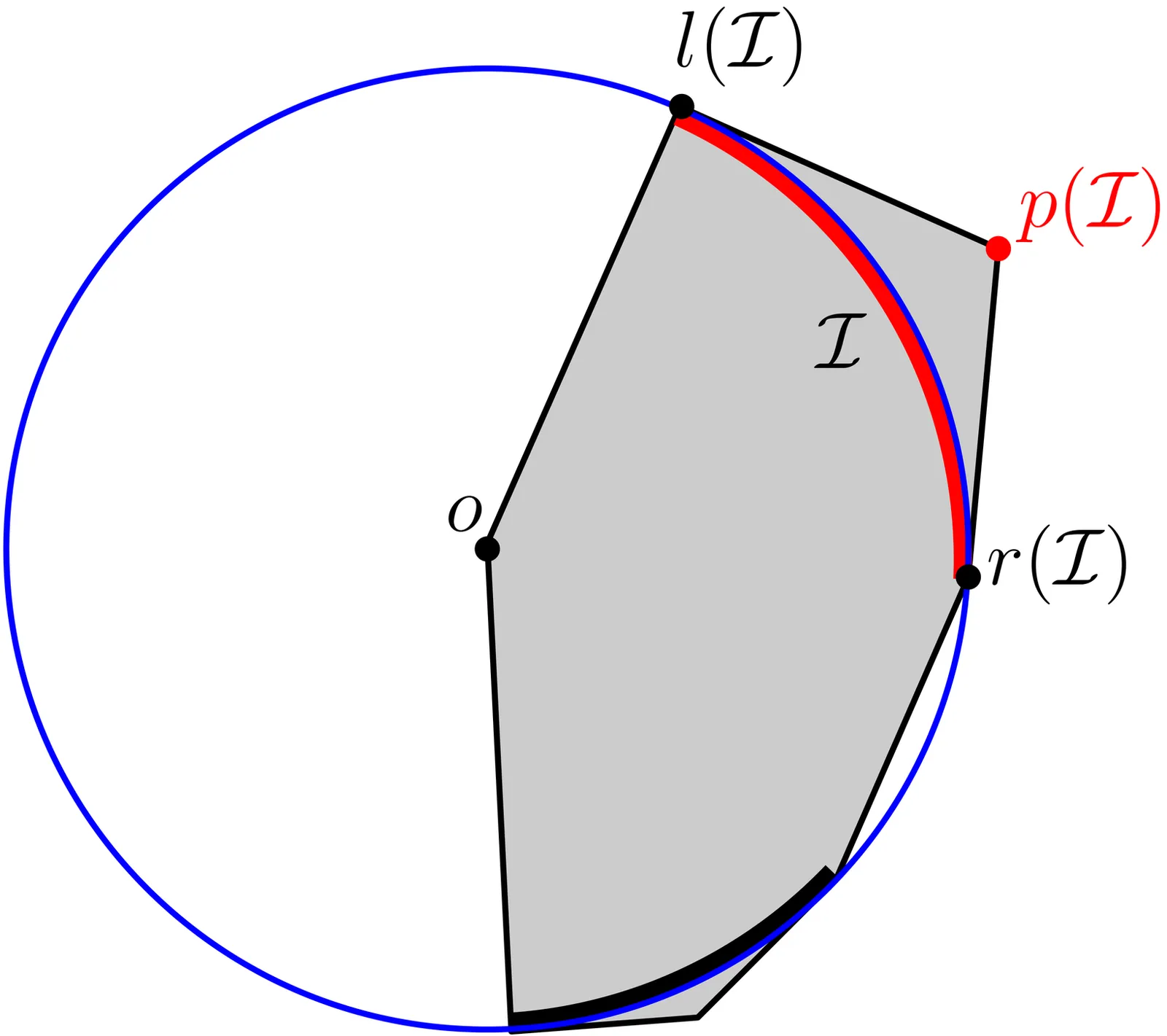
The 3SUM problem represents a class of problems conjectured to require $Ω(n^2)$ time to solve, where $n$ is the size of the input. Given two polygons $P$ and $Q$ in the plane, we show that some variants of the decision problem, whether there exists a transformation of $P$ that makes it contained in $Q$, are 3SUM-Hard. In the first variant $P$ and $Q$ are any simple polygons and the allowed transformations are translations only; in the second and third variants both polygons are convex and we allow either rotations only or any rigid motion. We also show that finding the translation in the plane that minimizes the Hausdorff distance between two segment sets is 3SUM-Hard.
2512.1418465Dec 2025
View
Fast computation of the first discrete homology group
We present a new algorithm for computing the first discrete homology group of a graph. By testing the algorithm on different data sets of random graphs, we find that it significantly outperforms other known algorithms.
2512.13929Dec 2025
View
VoroLight: Learning Quality Volumetric Voronoi Meshes from General Inputs
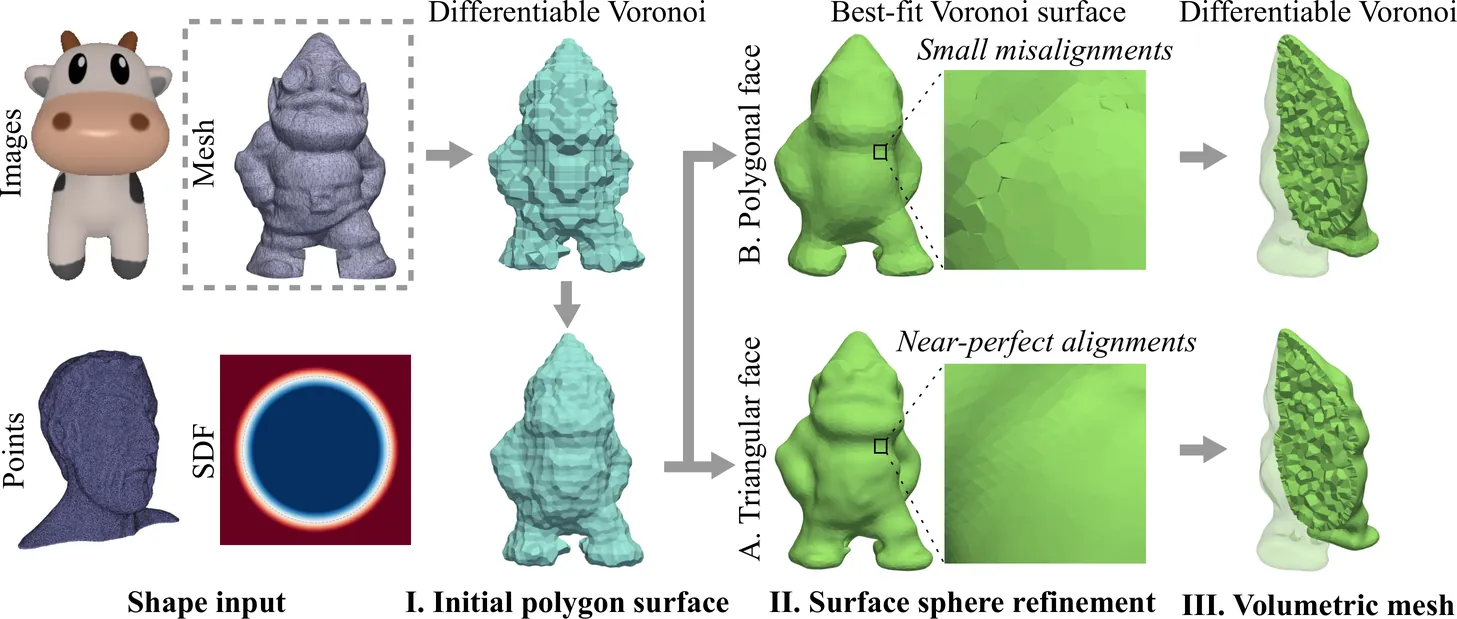
We present VoroLight, a differentiable framework for 3D shape reconstruction based on Voronoi meshing. Our approach generates smooth, watertight surfaces and topologically consistent volumetric meshes directly from diverse inputs, including images, implicit shape level-set fields, point clouds and meshes. VoroLight operates in three stages: it first initializes a surface using a differentiable Voronoi formulation, then refines surface quality through a polygon-face sphere training stage, and finally reuses the differentiable Voronoi formulation for volumetric optimization with additional interior generator points. Project page: https://jiayinlu19960224.github.io/vorolight/
2512.12984Dec 2025
View
Continuous Edit Distance, Geodesics and Barycenters of Time-varying Persistence Diagrams
We introduce the Continuous Edit Distance (CED), a geodesic and elastic distance for time-varying persistence diagrams (TVPDs). The CED extends edit-distance ideas to TVPDs by combining local substitution costs with penalized deletions/insertions, controlled by two parameters: \(α\) (trade-off between temporal misalignment and diagram discrepancy) and \(β\) (gap penalty). We also provide an explicit construction of CED-geodesics. Building on these ingredients, we present two practical barycenter solvers, one stochastic and one greedy, that monotonically decrease the CED Frechet energy. Empirically, the CED is robust to additive perturbations (both temporal and spatial), recovers temporal shifts, and supports temporal pattern search. On real-life datasets, the CED achieves clustering performance comparable or better than standard elastic dissimilarities, while our clustering based on CED-barycenters yields superior classification results. Overall, the CED equips TVPD analysis with a principled distance, interpretable geodesics, and practical barycenters, enabling alignment, comparison, averaging, and clustering directly in the space of TVPDs. A C++ implementation is provided for reproducibility at the following address https://github.com/sebastien-tchitchek/ContinuousEditDistance.
2512.12939Dec 2025
View
Efficiently Approximating the Minimum-Volume Bounding Box of a Point Set in Three Dimensions
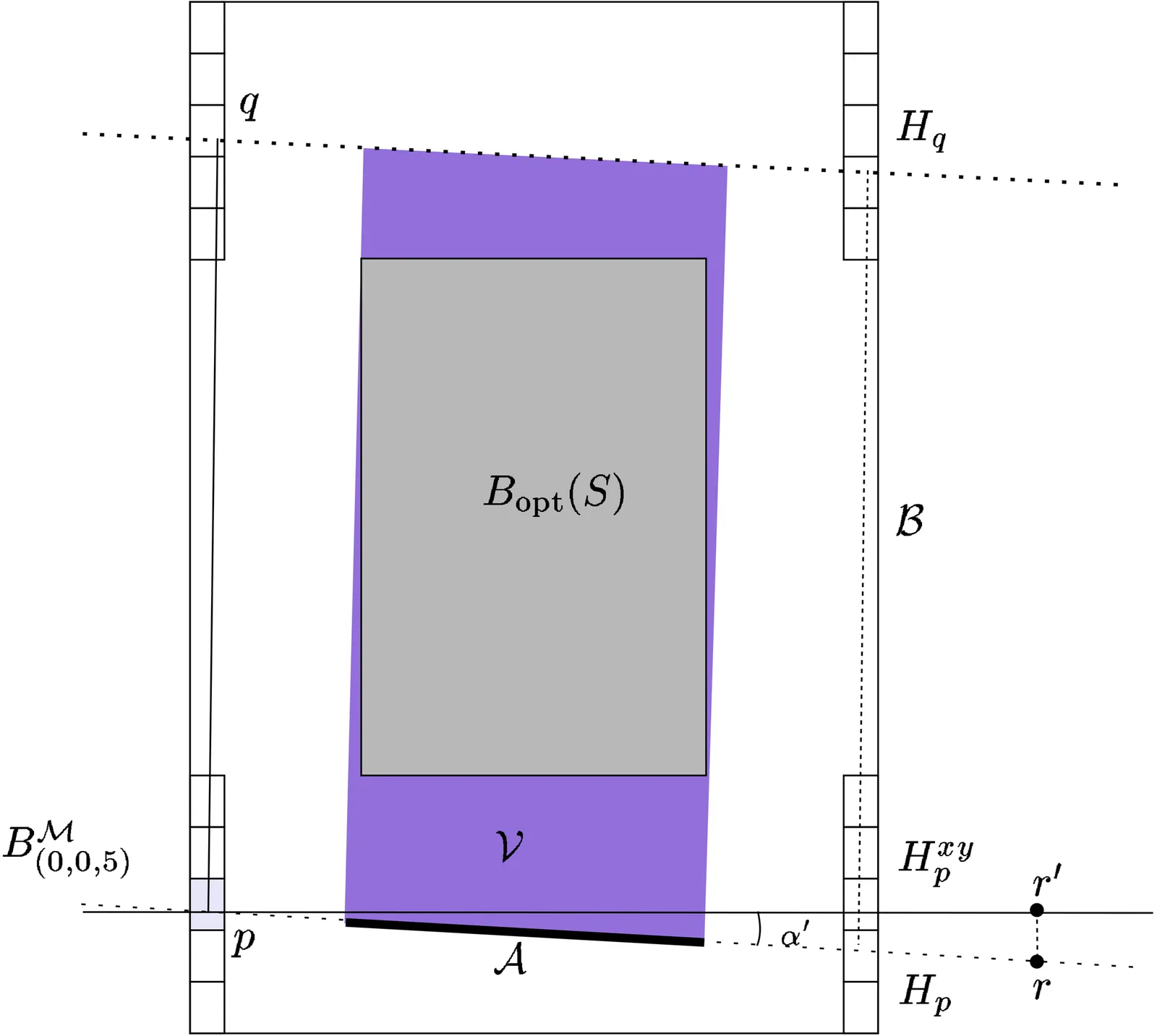
$\renewcommand{\Re}{\mathbb{R}}$We present an efficient $O (n + 1/\varepsilon^{4.5})$-time algorithm for computing a $(1+\varepsilon$)-approximation of the minimum-volume bounding box of $n$ points in $\Re^3$. We also present a simpler algorithm (for the same purpose) whose running time is $O (n \log{n} + n / \varepsilon^3)$. We give some experimental results with implementations of various variants of the second algorithm. The implementation of the algorithm described in this paper is available online https://github.com/sarielhp/MVBB.
2512.12391323Dec 2025
View
The Complexity of One or Many Faces in the Overlay of Many Arrangements
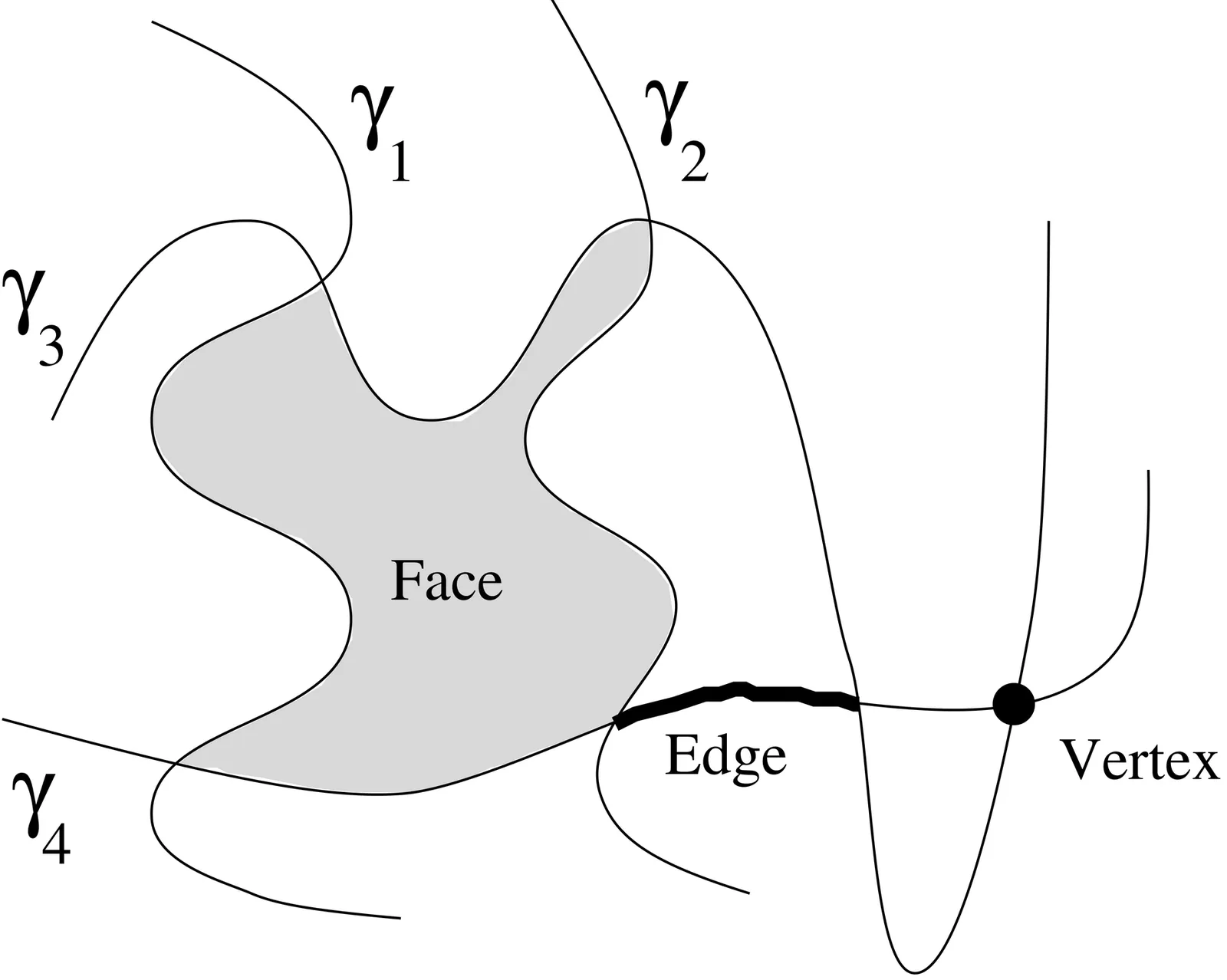
We present an extension of the Combination Lemma of [GSS89] that expresses the complexity of one or several faces in the overlay of many arrangements, as a function of the number of arrangements, the number of faces, and the complexities of these faces in the separate arrangements. Several applications of the new Combination Lemma are presented: We first show that the complexity of a single face in an arrangement of $k$ simple polygons with a total of $n$ sides is $Θ(n α(k) )$, where $α(\cdot)$ is the inverse of Ackermann's function. We also give a new and simpler proof of the bound $O \left( \sqrt{m} λ_{s+2}( n ) \right)$ on the total number of edges of $m$ faces in an arrangement of $n$ Jordan arcs, each pair of which intersect in at most $s$ points, where $λ_{s}(n)$ is the maximum length of a Davenport-Schinzel sequence of order $s$ with $n$ symbols. We extend this result, showing that the total number of edges of $m$ faces in a sparse arrangement of $n$ Jordan arcs is $O \left( (n + \sqrt{m}\sqrt{w}) \frac{λ_{s+2}(n)}{n} \right)$, where $w$ is the total complexity of the arrangement. Several other applications and variants of the Combination Lemma are also presented.
2512.11445Dec 2025
View
Shortest Paths on Convex Polyhedral Surfaces
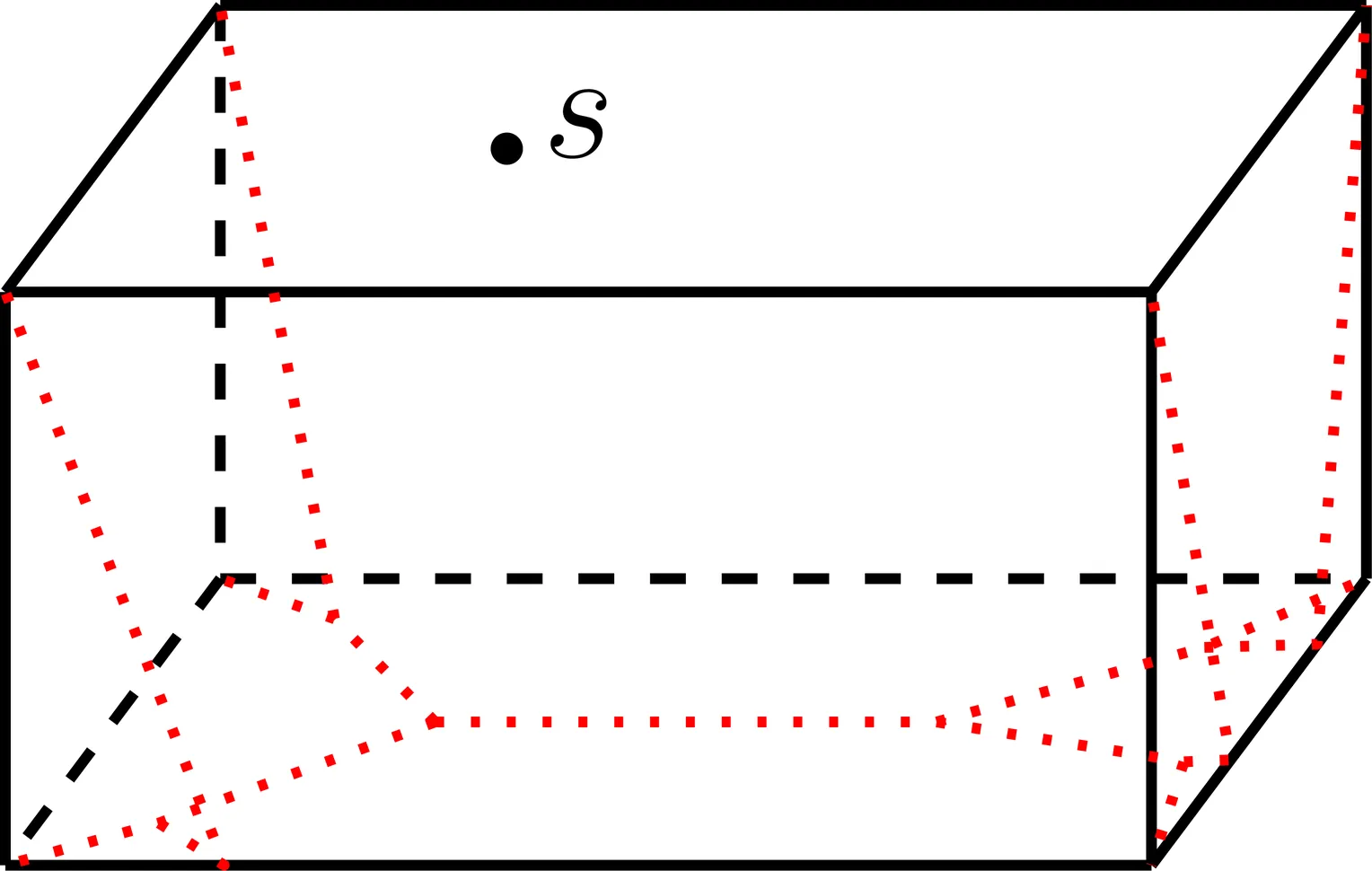
Let $\mathcal{P}$ be the surface of a convex polyhedron with $n$ vertices. We consider the two-point shortest path query problem for $\mathcal{P}$: Constructing a data structure so that given any two query points $s$ and $t$ on $\mathcal{P}$, a shortest path from $s$ to $t$ on $\mathcal{P}$ can be computed efficiently. To achieve $O(\log n)$ query time (for computing the shortest path length), the previously best result uses $O(n^{8+ε})$ preprocessing time and space [Aggarwal, Aronov, O'Rourke, and Schevon, SICOMP 1997], where $ε$ is an arbitrarily small positive constant. In this paper, we present a new data structure of $O(n^{6+ε})$ preprocessing time and space, with $O(\log n)$ query time. For a special case where one query point is required to lie on one of the edges of $\mathcal{P}$, the previously best work uses $O(n^{6+ε})$ preprocessing time and space to achieve $O(\log n)$ query time. We improve the preprocessing time and space to $O(n^{5+ε})$, with $O(\log n)$ query time. Furthermore, we present a new algorithm to compute the exact set of shortest path edge sequences of $\mathcal{P}$, which are known to be $Θ(n^4)$ in number and have a total complexity of $Θ(n^5)$ in the worst case. The previously best algorithm for the problem takes roughly $O(n^6\log n\log^*n)$ time, while our new algorithm runs in $O(n^{5+ε})$ time.
2512.11299Dec 2025
View
Approximating Euclidean Shallow-Light Trees
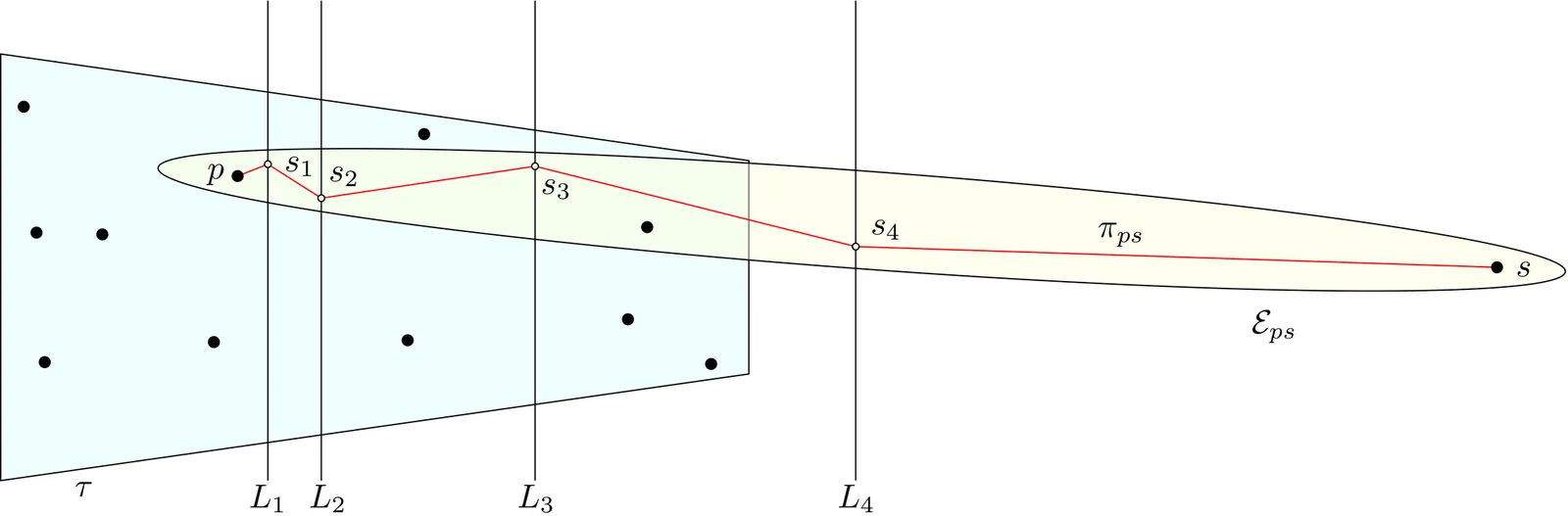
For a weighted graph $G = (V, E, w)$ and a designated source vertex $s \in V$, a spanning tree that simultaneously approximates a shortest-path tree w.r.t. source $s$ and a minimum spanning tree is called a shallow-light tree (SLT). Specifically, an $(α, β)$-SLT of $G$ w.r.t. $s \in V$ is a spanning tree of $G$ with root-stretch $α$ (preserving all distances between $s$ and the other vertices up to a factor of $α$) and lightness $β$ (its weight is at most $β$ times the weight of a minimum spanning tree of $G$). Despite the large body of work on SLTs, the basic question of whether a better approximation algorithm exists was left untouched to date, and this holds in any graph family. This paper makes a first nontrivial step towards this question by presenting two bicriteria approximation algorithms. For any $ε>0$, a set $P$ of $n$ points in constant-dimensional Euclidean space and a source $s\in P$, our first (respectively, second) algorithm returns, in $O(n \log n \cdot {\rm polylog}(1/ε))$ time, a non-Steiner (resp., Steiner) tree with root-stretch $1+O(ε\log ε^{-1})$ and weight at most $O(\mathrm{opt}_ε\cdot \log^2 ε^{-1})$ (resp., $O(\mathrm{opt}_ε\cdot \log ε^{-1})$), where $\mathrm{opt}_ε$ denotes the minimum weight of a non-Steiner (resp., Steiner) tree with root-stretch $1+ε$.
2512.10797Dec 2025
View
Quantifying displacement: a gentrification's consequence via persistent homology
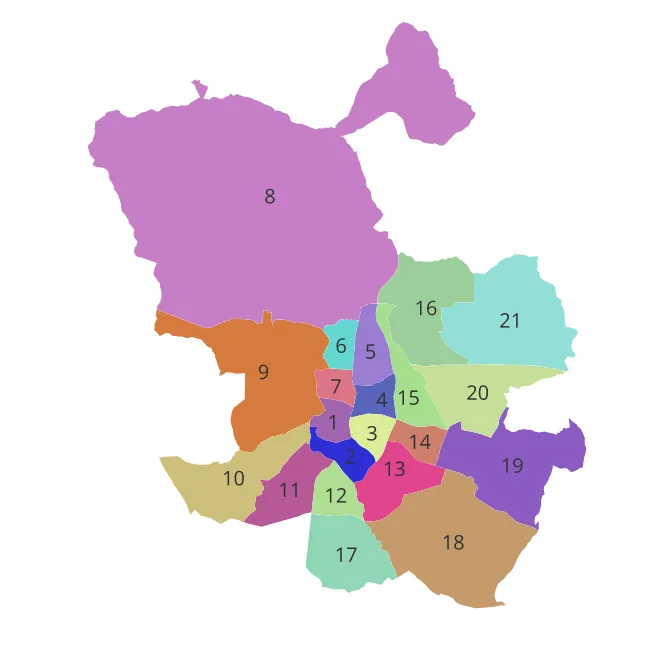
Gentrification is the process by which wealthier individuals move into a previously lower-income neighbourhood. Among the effects of this multi-faceted phenomenon are rising living costs, cultural and social changes-where local traditions, businesses, and community networks are replaced or diluted by new, more affluent lifestyles-and population displacement, where long-term, lower-income residents are priced out by rising rents and property taxes. Despite its relevance, quantifying displacement presents difficulties stemming from lack of information on motives for relocation and from the fact that a long time-span must be analysed: displacement is a gradual process (leases end or conditions change at different times), impossible to capture in one data snapshot. We introduce a novel tool to overcome these difficulties. Using only publicly available address change data, we construct four cubical complexes which simultaneously incorporate geographical and temporal information of people moving, and then analyse them building on Topological Data Analysis tools. Finally, we demonstrate the potential of this method through a 20-year case study of Madrid, Spain. The results reveal its ability to capture population displacement and to identify the specific neighbourhoods and years affected--patterns that cannot be inferred from raw address change data.
2512.10753Dec 2025
View
A gradient descent algorithm for computing circle patterns
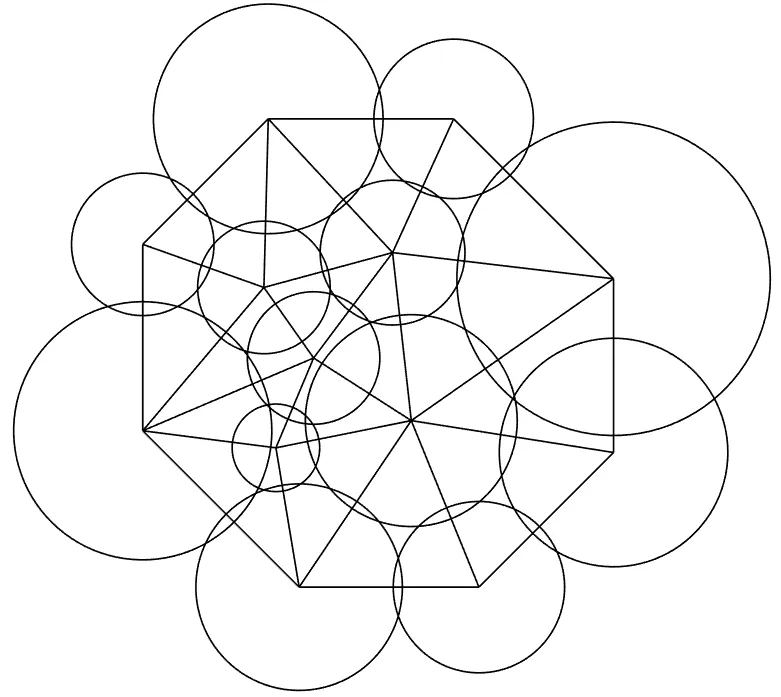
This paper presents a new algorithm for generating planar circle patterns. The algorithm employs gradient descent and conjugate gradient method to compute circle radii and centers separately. Compared with existing algorithms, the proposed method is more efficient in computing centers of circles and is applicable for realizing circle patterns with possible obtuse overlap angles.
2512.10387Dec 2025
View
Near-Linear and Parameterized Approximations for Maximum Cliques in Disk Graphs
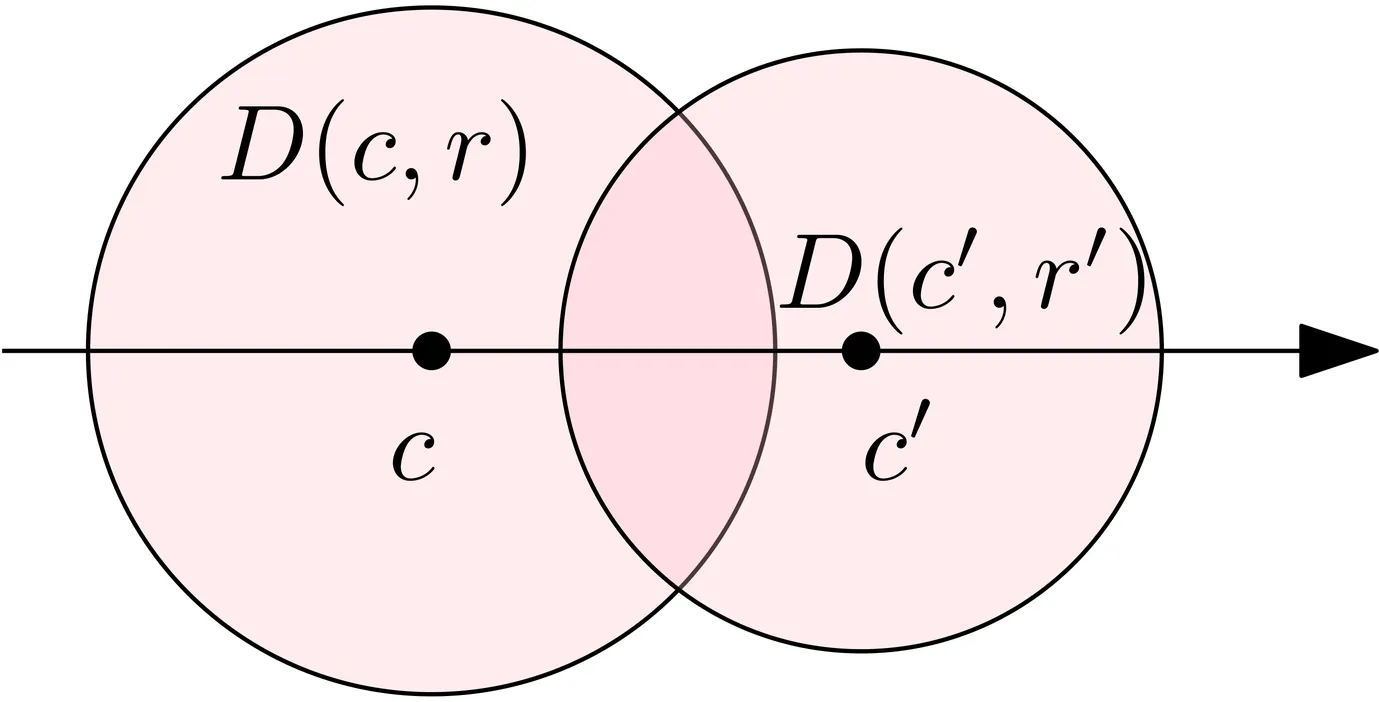
A \emph{disk graph} is the intersection graph of (closed) disks in the plane. We consider the classic problem of finding a maximum clique in a disk graph. For general disk graphs, the complexity of this problem is still open, but for unit disk graphs, it is well known to be in P. The currently fastest algorithm runs in time $O(n^{7/3+ o(1)})$, where $n$ denotes the number of disks~\cite{EspenantKM23, keil_et_al:LIPIcs.SoCG.2025.63}. Moreover, for the case of disk graphs with $t$ distinct radii, the problem has also recently been shown to be in XP. More specifically, it is solvable in time $O^*(n^{2t})$~\cite{keil_et_al:LIPIcs.SoCG.2025.63}. In this paper, we present algorithms with improved running times by allowing for approximate solutions and by using randomization: (i) for unit disk graphs, we give an algorithm that, with constant success probability, computes a $(1-\varepsilon)$-approximate maximum clique in expected time $\tilde{O}(n/\varepsilon^2)$; and (ii) for disk graphs with $t$ distinct radii, we give a parameterized approximation scheme that, with a constant success probability, computes a $(1-\varepsilon)$-approximate maximum clique in expected time $\tilde{O}(f(t)\cdot (1/\varepsilon)^{O(t)} \cdot n)$.
2512.09899Dec 2025
ViewPage 1 of 7
