Computational Complexity

arXiv:cs.CC

Covers models of computation, complexity classes, structural complexity, complexity tradeoffs, upper and lower bounds.

Looking for a broader view? This category is part of:

Trending in Computational Complexity

2511.06171

Halfspaces are hard to test with relative error

Several recent works [DHLNSY25, CPPS25a, CPPS25b] have studied a model of property testing of Boolean functions under a \emph{relative-error} criterion. In this model, the distance from a target function $f: \{0,1\}^n \to \{0,1\}$ that is being tested to a function $g$ is defined relative to the number of inputs $x$ for which $f(x)=1$; moreover, testing algorithms in this model have access both to a black-box oracle for $f$ and to independent uniform satisfying assignments of $f$. The motivation for this model is that it provides a natural framework for testing \emph{sparse} Boolean functions that have few satisfying assignments, analogous to well-studied models for property testing of sparse graphs. The main result of this paper is a lower bound for testing \emph{halfspaces} (i.e., linear threshold functions) in the relative error model: we show that $\tildeΩ(\log n)$ oracle calls are required for any relative-error halfspace testing algorithm over the Boolean hypercube $\{0,1\}^n$. This stands in sharp contrast both with the constant-query testability (independent of $n$) of halfspaces in the standard model [MORS10], and with the positive results for relative-error testing of many other classes given in [DHLNSY25, CPPS25a, CPPS25b]. Our lower bound for halfspaces gives the first example of a well-studied class of functions for which relative-error testing is provably more difficult than standard-model testing.

2511.06171

Nov 2025Computational Complexity

Related categories:

Data Structures and Algorithms Logic in Computer Science Formal Languages and Automata Theory Discrete Mathematics Combinatorics

195 papers

2601.03243

$\mathsf{QAC}^0$ Contains $\mathsf{TC}^0$ (with Many Copies of the Input)

$\mathsf{QAC}^0$ is the class of constant-depth polynomial-size quantum circuits constructed from arbitrary single-qubit gates and generalized Toffoli gates. It is arguably the smallest natural class of constant-depth quantum computation which has not been shown useful for computing any non-trivial Boolean function. Despite this, many attempts to port classical $\mathsf{AC}^0$ lower bounds to $\mathsf{QAC}^0$ have failed. We give one possible explanation of this: $\mathsf{QAC}^0$ circuits are significantly more powerful than their classical counterparts. We show the unconditional separation $\mathsf{QAC}^0\not\subset\mathsf{AC}^0[p]$ for decision problems, which also resolves for the first time whether $\mathsf{AC}^0$ could be more powerful than $\mathsf{QAC}^0$. Moreover, we prove that $\mathsf{QAC}^0$ circuits can compute a wide range of Boolean functions if given multiple copies of the input: $\mathsf{TC}^0 \subseteq \mathsf{QAC}^0 \circ \mathsf{NC}^0$. Along the way, we introduce an amplitude amplification technique that makes several approximate constant-depth constructions exact.

2601.03243Jan 2026

View

Hidden costs for inference with deep network on embedded system devices

This study evaluates the inference performance of various deep learning models under an embedded system environment. In previous works, Multiply-Accumulate operation is typically used to measure computational load of a deep model. According to this study, however, this metric has a limitation to estimate inference time on embedded devices. This paper poses the question of what aspects are overlooked when expressed in terms of Multiply-Accumulate operations. In experiments, an image classification task is performed on an embedded system device using the CIFAR-100 dataset to compare and analyze the inference times of ten deep models with the theoretically calculated Multiply-Accumulate operations for each model. The results highlight the importance of considering additional computations between tensors when optimizing deep learning models for real-time performing in embedded systems.

2601.01698Jan 2026

View

2512.23680

Coloring Hardness on Low Twin-Width Graphs

As the class $\mathcal T_4$ of graphs of twin-width at most 4 contains every finite subgraph of the infinite grid and every graph obtained by subdividing each edge of an $n$-vertex graph at least $2 \log n$ times, most NP-hard graph problems, like Max Independent Set, Dominating Set, Hamiltonian Cycle, remain so on $\mathcal T_4$. However, Min Coloring and k-Coloring are easy on both families because they are 2-colorable and 3-colorable, respectively. We show that Min Coloring is NP-hard on the class $\mathcal T_3$ of graphs of twin-width at most 3. This is the first hardness result on $\mathcal T_3$ for a problem that is easy on cographs (twin-width 0), on trees (whose twin-width is at most 2), and on unit circular-arc graphs (whose twin-width is at most 3). We also show that for every $k \geqslant 3$, k-Coloring is NP-hard on $\mathcal T_4$. We finally make two observations: (1) there are currently very few problems known to be in P on $\mathcal T_d$ (graphs of twin-width at most $d$) and NP-hard on $\mathcal T_{d+1}$ for some nonnegative integer $d$, and (2) unlike $\mathcal T_4$, which contains every graph as an induced minor, the class $\mathcal T_3$ excludes a fixed planar graph as an induced minor; thus it may be viewed as a special case (or potential counterexample) for conjectures about classes excluding a (planar) induced minor. These observations are accompanied by several open questions.

2512.23680Dec 2025

View

Analogy between List Coloring Problems and the Interval $k$-$(γ,μ)$-choosability property: theoretical aspects of complexity

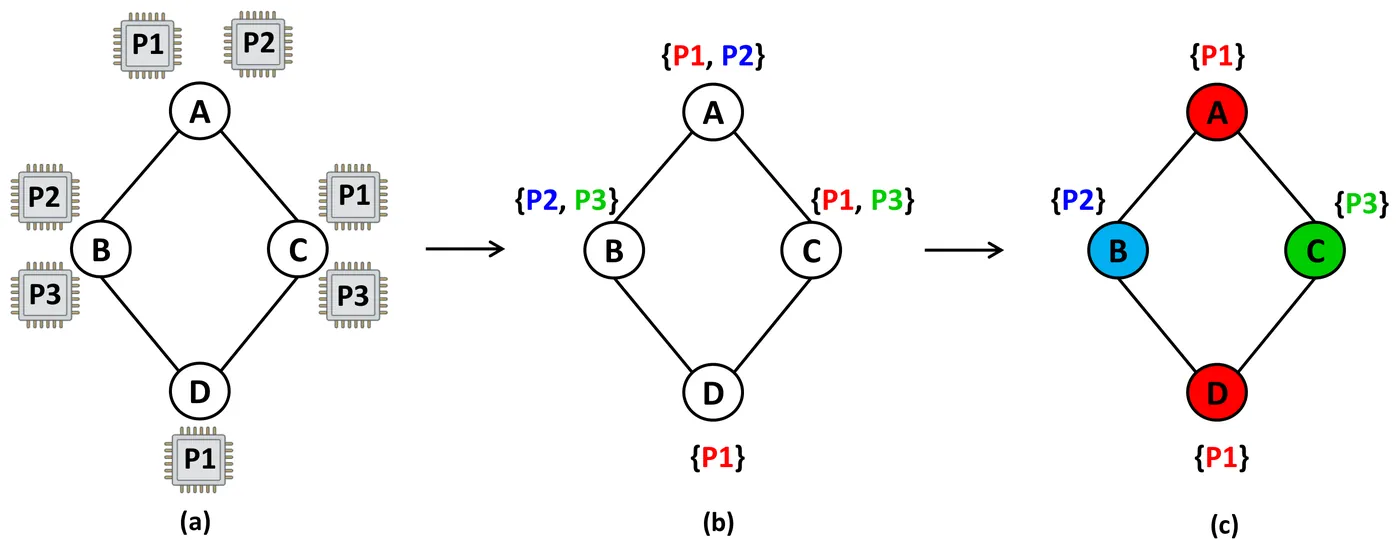
This work investigates structural and computational aspects of list-based graph coloring under interval constraints. Building on the framework of analogous and p-analogous problems, we show that classical List Coloring, $μ$-coloring, and $(γ,μ)$-coloring share strong complexity-preserving correspondences on graph classes closed under pendant-vertex extensions. These equivalences allow hardness and tractability results to transfer directly among the models. Motivated by applications in scheduling and resource allocation with bounded ranges, we introduce the interval-restricted $k$-$(γ,μ)$-coloring model, where each vertex receives an interval of exactly $k$ consecutive admissible colors. We prove that, although $(γ,μ)$-coloring is NP-complete even on several well-structured graph classes, its $k$-restricted version becomes polynomial-time solvable for any fixed $k$. Extending this formulation, we define $k$-$(γ,μ)$-choosability and analyze its expressive power and computational limits. Our results show that the number of admissible list assignments is drastically reduced under interval constraints, yielding a more tractable alternative to classical choosability, even though the general decision problem remains located at high levels of the polynomial hierarchy. Overall, the paper provides a unified view of list-coloring variants through structural reductions, establishes new complexity bounds for interval-based models, and highlights the algorithmic advantages of imposing fixed-size consecutive color ranges.

2512.16807Dec 2025

View

Hardness of SetCover Reoptimization

We study hardness of reoptimization of the fundamental and hard to approximate SetCover problem. Reoptimization considers an instance together with a solution and a modified instance where the goal is to approximate the modified instance while utilizing the information gained by solution to the related instance. We study four different types of reoptimization for (weighted) SetCover: adding a set, removing a set, adding an element to the universe, and removing an element from the universe. A few of these cases are known to be easier to approximate than the classic SetCover problem. We show that all the other cases are essentially as hard to approximate as SetCover. The reoptimization problem of adding and removing an element in the unweighted case is known to admit a PTAS. For these settings we show that there is no EPTAS under common hardness assumptions via a novel combination of the classic way to show that a reoptimization problem is NP-hard and the relation between EPTAS and FPT.

2512.16805Dec 2025

View

2512.16082

Good Locally Testable Codes with Small Alphabet and Small Query Size

Ben-Sasson, Goldreich and Sudan showed that a binary error correcting code admitting a $2$-query tester cannot be good, i.e., it cannot have both linear distance and positive rate. The same holds when the alphabet is a finite field $\mathbb{F}$, the code is $\mathbb{F}$-linear, and the $2$-query tester is $\mathbb{F}$-linear. We show that those are essentially the only limitations on the existence of good locally testable codes (LTCs). That is, there are good $2$-query LTCs on any alphabet with more than $2$ letters, and good $3$-query LTCs with a binary alphabet. Similarly, there are good $3$-query $\mathbb{F}$-linear LTCs, and for every $\mathbb{F}$-vector space $V$ of dimension greater than $1$, there are good $2$-query LTCs with alphabet $V$ whose tester is $\mathbb{F}$-linear. This completely solves, for every $q\geq 2$ and alphabet (resp. $\mathbb{F}$-vector space) $Σ$, the question of whether there is a good $q$-query LTC (resp. $\mathbb{F}$-LTC) with alphabet $Σ$. Our proof builds on the recent good $2$-query $\mathbb{F}$-LTCs of the first author and Kaufman, by establishing a general method for reducing the alphabet size of a low-query LTC.

2512.16082Dec 2025

View

2512.13566

A Distance Amplification Lemma for Monotonicity

We show a procedure that, given oracle access to a function $f\colon \{0,1\}^n\to\{0,1\}$, produces oracle access to a function $f'\colon \{0,1\}^{n'}\to\{0,1\}$ such that if $f$ is monotone, then $f'$ is monotone, and if $f$ is $\varepsilon$-far from monotone, then $f'$ is $Ω(1)$-far from monotone. Moreover, $n' \leq n 2^{O(1/\varepsilon)}$ and each oracle query to $f'$ can be answered by making $2^{O(1/\varepsilon)}$ oracle queries to $f$. Our lemma is motivated by a recent result of [Chen, Chen, Cui, Pires, Stockwell, arXiv:2511.04558], who showed that for all $c>0$ there exists $\varepsilon_c>0$, such that any (even two-sided, adaptive) algorithm distinguishing between monotone functions and $\varepsilon_c$-far from monotone functions, requires $Ω(n^{1/2-c})$ queries. Combining our lemma with their result implies a similar result, except that the distance from monotonicity is an absolute constant $\varepsilon>0$, and the lower bound is $Ω(n^{1/2-o(1)})$ queries.

2512.13566Dec 2025

View

Homomorphism Indistinguishability, Multiplicity Automata Equivalence, and Polynomial Identity Testing

Two graphs $G$ and $H$ are homomorphism indistinguishable over a graph class $\mathcal{F}$ if they admit the same number of homomorphisms from every graph $F \in \mathcal{F}$. Many graph isomorphism relaxations such as (quantum) isomorphism and cospectrality can be characterised as homomorphism indistinguishability over specific graph classes. Thereby, the problems $\textrm{HomInd}(\mathcal{F})$ of deciding homomorphism indistinguishability over $\mathcal{F}$ subsume diverse graph isomorphism relaxations whose complexities range from logspace to undecidable. Establishing the first general result on the complexity of $\textrm{HomInd}(\mathcal{F})$, Seppelt (MFCS 2024) showed that $\textrm{HomInd}(\mathcal{F})$ is in randomised polynomial time for every graph class $\mathcal{F}$ of bounded treewidth that can be defined in counting monadic second-order logic $\mathsf{CMSO}_2$. We show that this algorithm is conditionally optimal, i.e. it cannot be derandomised unless polynomial identity testing is in $\mathsf{PTIME}$. For $\mathsf{CMSO}_2$-definable graph classes $\mathcal{F}$ of bounded pathwidth, we improve the previous complexity upper bound for $\textrm{HomInd}(\mathcal{F})$ from $\mathsf{PTIME}$ to $\mathsf{C}_=\mathsf{L}$ and show that this is tight. Secondarily, we establish a connection between homomorphism indistinguishability and multiplicity automata equivalence which allows us to pinpoint the complexity of the latter problem as $\mathsf{C}_=\mathsf{L}$-complete.

2512.13058Dec 2025

View

2512.12960

3-Query RLDCs are Strictly Stronger than 3-Query LDCs

We construct $3$-query relaxed locally decodable codes (RLDCs) with constant alphabet size and length $\tilde{O}(k^2)$ for $k$-bit messages. Combined with the lower bound of $\tildeΩ(k^3)$ of [Alrabiah, Guruswami, Kothari, Manohar, STOC 2023] on the length of locally decodable codes (LDCs) with the same parameters, we obtain a separation between RLDCs and LDCs, resolving an open problem of [Ben-Sasson, Goldreich, Harsha, Sudan and Vadhan, SICOMP 2006]. Our RLDC construction relies on two components. First, we give a new construction of probabilistically checkable proofs of proximity (PCPPs) with $3$ queries, quasi-linear size, constant alphabet size, perfect completeness, and small soundness error. This improves upon all previous PCPP constructions, which either had a much higher query complexity or soundness close to $1$. Second, we give a query-preserving transformation from PCPPs to RLDCs. At the heart of our PCPP construction is a $2$-query decodable PCP (dPCP) with matching parameters, and our construction builds on the HDX-based PCP of [Bafna, Minzer, Vyas, Yun, STOC 2025] and on the efficient composition framework of [Moshkovitz, Raz, JACM 2010] and [Dinur, Harsha, SICOMP 2013]. More specifically, we first show how to use the HDX-based construction to get a dPCP with matching parameters but a large alphabet size, and then prove an appropriate composition theorem (and related transformations) to reduce the alphabet size in dPCPs.

2512.12960Dec 2025

View

Bounded Dynamic Level Maintenance for Efficient Logic Optimization

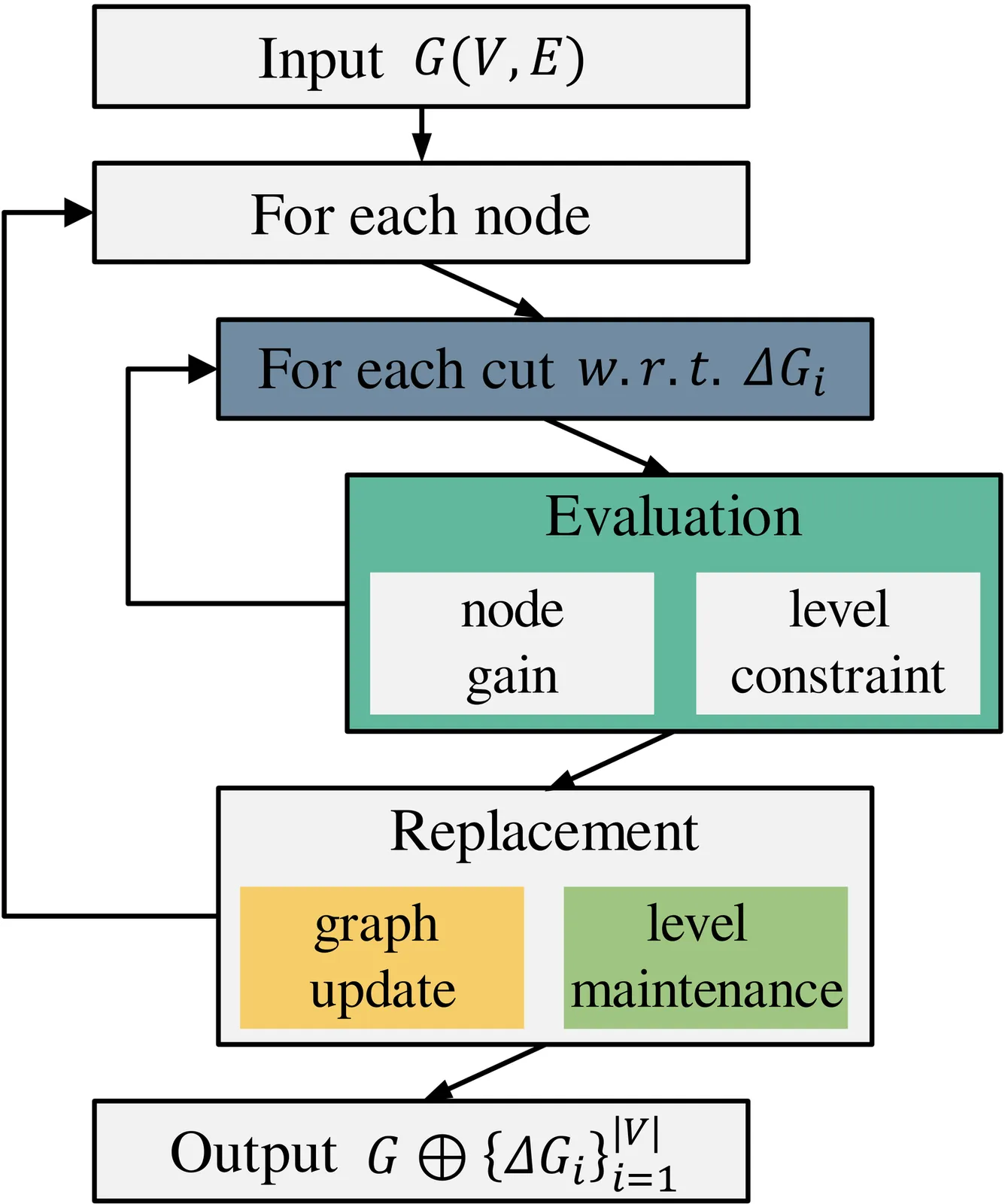
Logic optimization constitutes a critical phase within the Electronic Design Automation (EDA) flow, essential for achieving desired circuit power, performance, and area (PPA) targets. These logic circuits are typically represented as Directed Acyclic Graphs (DAGs), where the structural depth, quantified by node level, critically correlates with timing performance. Modern optimization strategies frequently employ iterative, local transformation heuristics (\emph{e.g.,} \emph{rewrite}, \emph{refactor}) directly on this DAG structure. As optimization continuously modifies the graph locally, node levels require frequent dynamic updates to guide subsequent decisions. However, a significant gap exists: existing algorithms for incrementally updating node levels are unbounded to small changes. This leads to a total of worst complexity in $O(|V|^2)$ for given local subgraphs $\{ΔG_i\}_{i=1}^{|V|}$ updates on DAG $G(V,E)$. This unbounded nature poses a severe efficiency bottleneck, hindering the scalability of optimization flows, particularly when applied to large circuit designs prevalent today. In this paper, we analyze the dynamic level maintenance problem endemic to iterative logic optimization, framing it through the lens of partial topological order. Building upon the analysis, we present the first bounded algorithm for maintaining level constraints, with $O(|V| Δ\log Δ)$ time for a sequence $|V|$ of updates $\{ΔG_i\}$, where $Δ= \max_i \|ΔG_i\|$ denotes the maximum extended size of $ΔG_i$. Experiments on comprehensive benchmarks show our algorithm enables an average 6.4$\times$ overall speedup relative to \rw and \rf, driven by a 1074.8$\times$ speedup in the level maintenance, all without any quality sacrifice.

2512.12554Dec 2025

View

2512.10635

Equivalent Instances for Scheduling and Packing Problems

Two instances $(I,k)$ and $(I',k')$ of a parameterized problem $P$ are equivalent if they have the same set of solutions (static equivalent) or if the set of solutions of $(I,k)$ can be constructed by the set of solutions for $(I',k')$ and some computable pre-solutions. If the algorithm constructing such a (static) equivalent instance whose size is polynomial bounded runs in fixed-parameter tractable (FPT) time, we say that there exists a (static) equivalent instance for this problem. In this paper we present (static) equivalent instances for Scheduling and Knapsack problems. We improve the bound for the $\ell_1$-norm of an equivalent vector given by Eisenbrand, Hunkenschröder, Klein, Koutecký, Levin, and Onn and show how this yields equivalent instances for integer linear programs (ILPs) and related problems. We obtain an $O(MN^2\log(NU))$ static equivalent instance for feasibility ILPs where $M$ is the number of constraints, $N$ is the number of variables and $U$ is an upper bound for the $\ell_\infty$-norm of the smallest feasible solution. With this, we get an $O(n^2\log(n))$ static equivalent instance for Knapsack where $n$ is the number of items. Moreover, we give an $O(M^2N\log(NMΔ))$ kernel for feasibility ILPs where $Δ$ is an upper bound for the $\ell_\infty$-norm of the given constraint matrix. Using balancing results by Knop et al., the ConfILP and a proximity result by Eisenbrand and Weismantel we give an $O(d^2\log(p_{\max}))$ equivalent instance for LoadBalancing, a generalization of scheduling problems. Here $d$ is the number of different processing times and $p_{\max}$ is the largest processing time.

2512.10635Dec 2025

View

From Alternation to FPRAS: Toward a Complexity Classification of Approximate Counting

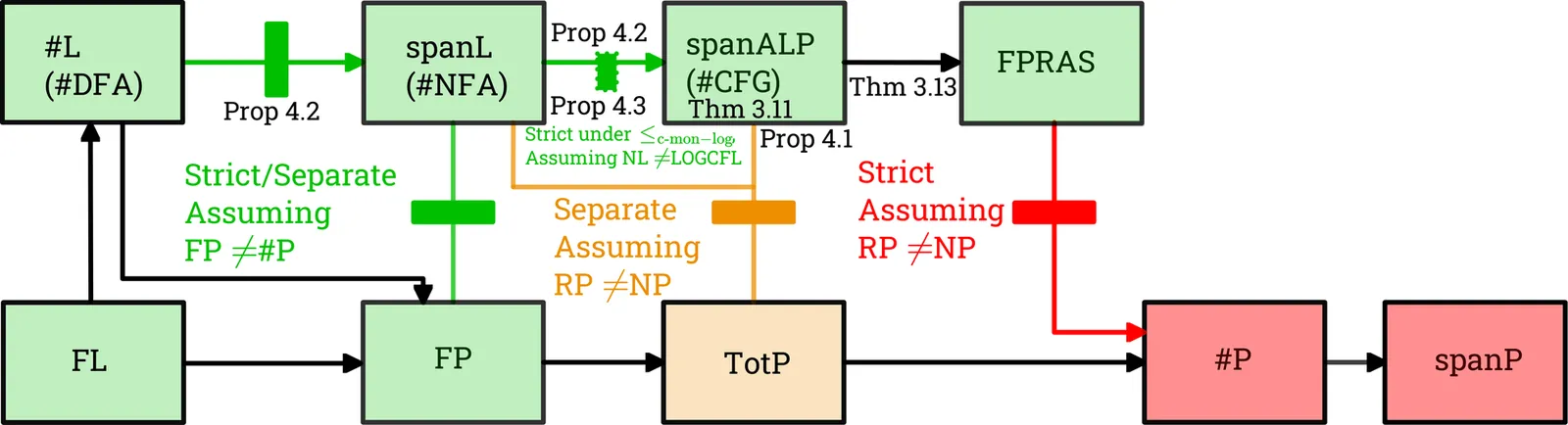
Counting problems are fundamental across mathematics and computer science. Among the most subtle are those whose associated decision problem is solvable in polynomial time, yet whose exact counting version appears intractable. For some such problems, however, one can still obtain efficient randomized approximation in the form of a fully polynomial randomized approximation scheme (FPRAS). Existing proofs of FPRAS existence are often highly technical and problem-specific, offering limited insight into a more systematic complexity-theoretic account of approximability. In this work, we propose a machine-based framework for establishing the existence of an FPRAS beyond previous uniform criteria. Our starting point is alternating computation: we introduce a counting model obtained by equipping alternating Turing machines with a transducer-style output mechanism, and we use it to define a corresponding counting class spanALP. We show that every problem in spanALP admits an FPRAS, yielding a reusable sufficient condition that can be applied via reductions to alternating logspace, polynomial-time computation with output. We situate spanALP in the counting complexity landscape as strictly between #L and TotP (assuming RP $\neq$ NP) and observe interesting conceptual and technical gaps in the current machinery counting complexity. Moreover, as an illustrative application, we obtain an FPRAS for counting answers to counting the answers Dyck-constrained path queries in edge-labeled graphs, i.e., counting the number of distinct labelings realized by s-t walks whose label sequence is well-formed with respect to a Dyck-like language. To our knowledge, no FPRAS was previously known for this setting. We expect the alternating-transducer characterization to provide a broadly applicable tool for establishing FPRAS existence for further counting problems.

2512.10472Dec 2025

View

2512.10385

Improved Small Set Expansion in High Dimensional Expanders

Small set expansion in high dimensional expanders is of great importance, e.g., towards proving cosystolic expansion, local testability of codes and constructions of good quantum codes. In this work we improve upon the state of the art results of small set expansion in high dimensional expanders. Our improvement is either on the expansion quality or on the size of sets for which expansion is guaranteed. One line of previous works [KM22, DD24] has obtained weak expansion for small sets, which is sufficient for deducing cosystolic expansion of one dimension below. We improve upon their result by showing strong expansion for small sets. Another line of works [KKL14, EK16, KM21] has shown strong expansion for small sets. However, they obtain it only for very small sets. We get an exponential improvement on the size of sets for which expansion is guaranteed by these prior works. Interestingly, our result is obtained by bridging between these two lines of works. The works of [KM22, DD24] use global averaging operators in order to obtain expansion for larger sets. However, their method could be utilized only on sets that are cocycle-like. We show how to combine these global averaging operators with ideas from the so-called ``fat machinery'' of [KKL14, EK16, KM21] in order to apply them for general sets.

2512.10385Dec 2025

View

Derandomizing Isolation In Catalytic Logspace

A language is said to be in catalytic logspace if we can test membership using a deterministic logspace machine that has an additional read/write tape filled with arbitrary data whose contents have to be restored to their original value at the end of the computation. The model of catalytic computation was introduced by Buhrman et al [STOC2014]. As our first result, we obtain a catalytic logspace algorithm for computing a minimum weight witness to a search problem, with small weights, provided the algorithm is given oracle access for the corresponding weighted decision problem. In particular, our reduction yields CL algorithms for the search versions of the following three problems: planar perfect matching, planar exact perfect matching and weighted arborescences in weighted digraphs. Our second set of results concern the significantly larger class CL^{NP}_{2-round}. We show that CL^{NP}_{2-round} contains SearchSAT and the complexity classes BPP, MA and ZPP^{NP[1]}. While SearchSAT is shown to be in CL^{NP}_{2-round} using the isolation lemma, the other three containments, while based on the compress-or-random technique, use the Nisan-Wigderson [JCSS 1994] based pseudo-random generator. These containments show that CL^{NP}_{2-round} resembles ZPP^NP more than P^{NP}, providing some weak evidence that CL is more like ZPP than P. For our third set of results we turn to isolation well inside catalytic classes. We consider the unambiguous catalytic class CTISP[poly(n),logn,log^2n]^UL and show that it contains reachability and therefore NL. This is a catalytic version of the result of van Melkebeek & Prakriya [SIAM J. Comput. 2019]. Building on their result, we also show a tradeoff between the workspace of the oracle and the catalytic space of the base machine. Finally, we extend these catalytic upper bounds to LogCFL.

2512.09374Dec 2025

View

2512.08268

Direct Product Theorems for Randomized Query Complexity

We establish two new direct product theorems for the randomized query complexity of Boolean functions. The first shows that computing $n$ copies of a function $f$, even with a small success probability of $γ^n$, requires $Θ(n)$ times the "maximum distributional" query complexity of $f$ with success parameter $γ$. This result holds for all success parameters $γ$, even when $γ$ is very close to $1/2$ or to $1$. As a result, it unifies and generalizes Drucker's direct product theorem (2012) for $γ$ bounded away from $\frac12$ and $1$ as well as the strong direct sum theorem of Blais and Brody (2019) for $γ\approx 1-1/n$. The second establishes a general "list decoding" direct product theorem that captures many different variants of partial computation tasks related to the function $f^n$ consisting of $n$ copies of $f$. Notably, our list decoding direct product theorem yields a new threshold direct product theorem and other new variants such as the labelled-threshold direct product theorem. Both of these direct product theorems are obtained by taking a new approach. Instead of directly analyzing the query complexity of algorithms, we introduce a new measure of complexity of functions that we call "discounted score". We show that this measure satisfies a number of useful structural properties, including tensorization, that make it particularly suitable for the study of direct product questions.

2512.08268Dec 2025

View

MAX BISECTION might be harder to approximate than MAX CUT

The MAX BISECTION problem seeks a maximum-size cut that evenly divides the vertices of a given undirected graph. An open problem raised by Austrin, Benabbas, and Georgiou is whether MAX BISECTION can be approximated as well as MAX CUT, i.e., to within ${α_{GW}}\approx 0.8785672\ldots$, which is the approximation ratio achieved by the celebrated Goemans-Williamson algorithm for MAX CUT, which is best possible assuming the Unique Games Conjecture (UGC). They conjectured that the answer is yes. The current paradigm for obtaining approximation algorithms for MAX BISECTION, due to Raghavendra and Tan and Austrin, Benabbas, and Georgiou, follows a two-phase approach. First, a large number of rounds of the Sum-of-Squares (SoS) hierarchy is used to find a solution to the ``Basic SDP'' relaxation of MAX CUT which is $\varepsilon$-uncorrelated, for an arbitrarily small $\varepsilon > 0$. Second, standard SDP rounding techniques (such as ${\cal THRESH}$) are used to round this $\varepsilon$-uncorrelated solution, producing with high probability a cut that is almost balanced, i.e., a cut that has at most $\frac12+\varepsilon$ fraction of the vertices on each side. This cut is then converted into an exact bisection of the graph with only a small loss. In this paper, we show that this two-stage paradigm cannot be used to obtain an $α_{GW}$-approximation algorithm for MAX BISECTION if one relies only on the $\varepsilon$-uncorrelatedness property of the solution produced by the first phase. More precisely, for any $\varepsilon > 0$, we construct an explicit instance of MAX BISECTION for which the ratio between the value of the optimal integral solution and the value of some $\varepsilon$-uncorrelated solution of the Basic SDP relaxation is less than $0.87853 < {α_{GW}}$. Our instances are also integrality gaps for the Basic SDP relaxation of MAX BISECTION.

2512.04951Dec 2025

View

Hardware-aware Neural Architecture Search of Early Exiting Networks on Edge Accelerators

Advancements in high-performance computing and cloud technologies have enabled the development of increasingly sophisticated Deep Learning (DL) models. However, the growing demand for embedded intelligence at the edge imposes stringent computational and energy constraints, challenging the deployment of these large-scale models. Early Exiting Neural Networks (EENN) have emerged as a promising solution, allowing dynamic termination of inference based on input complexity to enhance efficiency. Despite their potential, EENN performance is highly influenced by the heterogeneity of edge accelerators and the constraints imposed by quantization, affecting accuracy, energy efficiency, and latency. Yet, research on the automatic optimization of EENN design for edge hardware remains limited. To bridge this gap, we propose a hardware-aware Neural Architecture Search (NAS) framework that systematically integrates the effects of quantization and hardware resource allocation to optimize the placement of early exit points within a network backbone. Experimental results on the CIFAR-10 dataset demonstrate that our NAS framework can discover architectures that achieve over a 50\% reduction in computational costs compared to conventional static networks, making them more suitable for deployment in resource-constrained edge environments.

2512.04705Dec 2025

View

New Perspectives on Semiring Applications to Dynamic Programming

Semiring algebras have been shown to provide a suitable language to formalize many noteworthy combinatorial problems. For instance, the Shortest-Path problem can be seen as a special case of the Algebraic-Path problem when applied to the tropical semiring. The application of semirings typically makes it possible to solve extended problems without increasing the computational complexity. In this article we further exploit the idea of using semiring algebras to address and tackle several extensions of classical computational problems by dynamic programming. We consider a general approach which allows us to define a semiring extension of any problem with a reasonable notion of a certificate (e.g., an NP problem). This allows us to consider cost variants of these combinatorial problems, as well as their counting extensions where the goal is to determine how many solutions a given problem admits. The approach makes no particular assumptions (such as idempotence) on the semiring structure. We also propose a new associative algebraic operation on semirings, called $Δ$-product, which enables our dynamic programming algorithms to count the number of solutions of minimal costs. We illustrate the advantages of our framework on two well-known but computationally very different NP-hard problems, namely, Connected-Dominating-Set problems and finite-domain Constraint Satisfaction Problems (CSPs). In particular, we prove fixed parameter tractability (FPT) with respect to clique-width and tree-width of the input. This also allows us to count solutions of minimal cost, which is an overlooked problem in the literature.

2512.039161Dec 2025

View

Computing Equilibrium Points of Electrostatic Potentials

We study the computation of equilibrium points of electrostatic potentials: locations in space where the electrostatic force arising from a collection of charged particles vanishes. This is a novel scenario of optimization in which solutions are guaranteed to exist due to a nonconstructive argument, but gradient descent is unreliable due to the presence of singularities. We present an algorithm based on piecewise approximation of the potential function by Taylor series. The main insight is to divide the domain into a grid with variable coarseness, where grid cells are exponentially smaller in regions where the function changes rapidly compared to regions where it changes slowly. Our algorithm finds approximate equilibrium points in time poly-logarithmic in the approximation parameter, but these points are not guaranteed to be close to exact solutions. Nevertheless, we show that such points can be computed efficiently under a mild assumption that we call "strong non-degeneracy". We complement these algorithmic results by studying a generalization of this problem and showing that it is CLS-hard and in PPAD, leaving its precise classification as an intriguing open problem.

2512.03249Dec 2025

View

Permanental rank versus determinantal rank of random matrices over finite fields

This paper is motivated by basic complexity and probability questions about permanents of random matrices over finite fields, and in particular, about properties separating the permanent and the determinant. Fix $q = p^m$ some power of an odd prime, and let $k \leq n$ both be growing. For a uniformly random $n \times k$ matrix $A$ over $\mathbb{F}_q$, we study the probability that all $k \times k$ submatrices of $A$ have zero permanent; namely that $A$ does not have full "permanental rank". When $k = n$, this is simply the probability that a random square matrix over $\mathbb{F}_q$ has zero permanent, which we do not understand. We believe that the probability in this case is $\frac{1}{q} + o(1)$, which would be in contrast to the case of the determinant, where the answer is $\frac{1}{q} + Ω_q(1)$. Our main result is that when $k$ is $O(\sqrt{n})$, the probability that a random $n \times k$ matrix does not have full permanental rank is essentially the same as the probability that the matrix has a $0$ column, namely $(1 +o(1)) \frac{k}{q^n}$. In contrast, for determinantal (standard) rank the analogous probability is $Θ(\frac{q^k}{q^n})$. At the core of our result are some basic linear algebraic properties of the permanent that distinguish it from the determinant.

2512.03221Dec 2025

View

Page 1 of 10