Pricing of Securities
arXiv:q-fin.PR
Valuation and hedging of financial securities, derivative markets, pricing models.
Looking for a broader view? This category is part of:
10 papers
Reinforcement Learning for Option Hedging: Static Implied-Volatility Fit versus Shortfall-Aware Performance
We extend the Q-learner in Black-Scholes (QLBS) framework by incorporating risk aversion and trading costs, and propose a novel Replication Learning of Option Pricing (RLOP) approach. Both methods are fully compatible with standard reinforcement learning algorithms and operate under market frictions. Using SPY and XOP option data, we evaluate performance along static and dynamic dimensions. Adaptive-QLBS achieves higher static pricing accuracy in implied volatility space, while RLOP delivers superior dynamic hedging performance by reducing shortfall probability. These results highlight the importance of evaluating option pricing models beyond static fit, emphasizing realized hedging outcomes.
2601.01709Jan 2026
View
Machine learning models for predicting catastrophe bond coupons using climate data
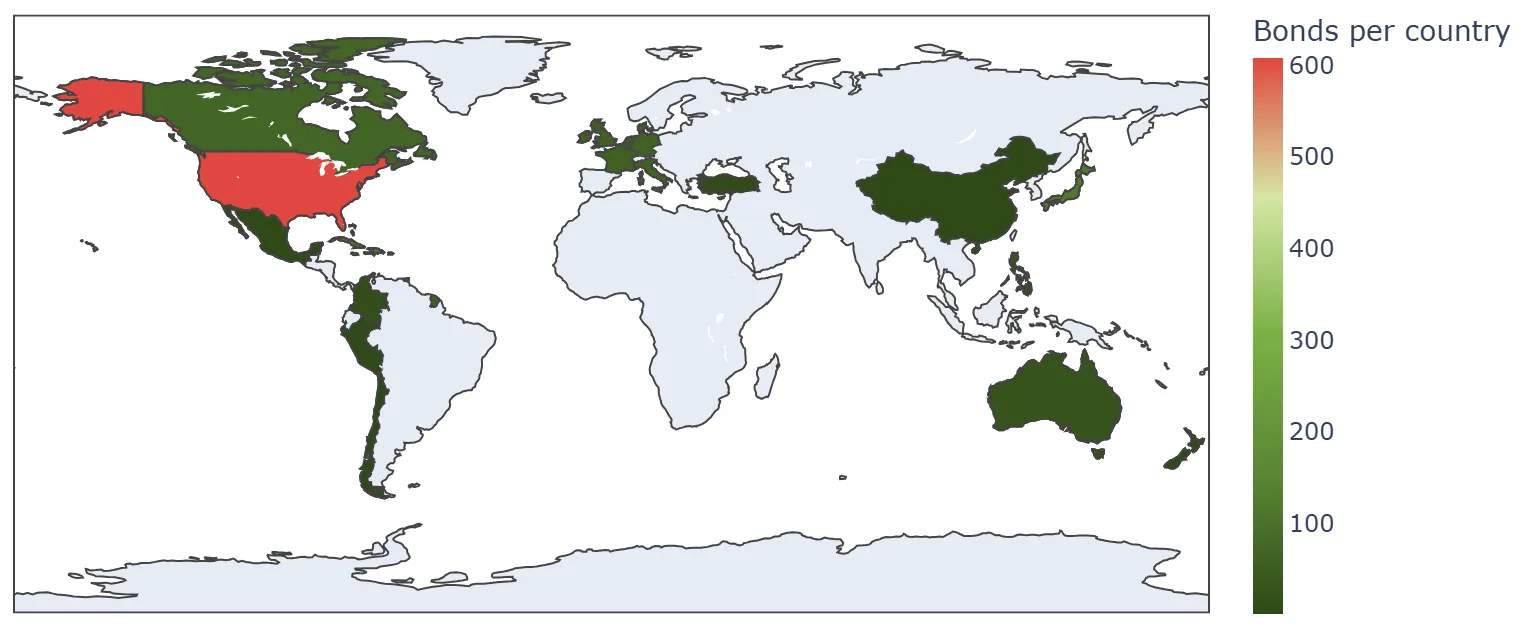
In recent years, the growing frequency and severity of natural disasters have increased the need for effective tools to manage catastrophe risk. Catastrophe (CAT) bonds allow the transfer of part of this risk to investors, offering an alternative to traditional reinsurance. This paper examines the role of climate variability in CAT bond pricing and evaluates the predictive performance of various machine learning models in forecasting CAT bond coupons. We combine features typically used in the literature with a new set of climate indicators, including Oceanic Ni{ñ}o Index, Arctic Oscillation, North Atlantic Oscillation, Outgoing Longwave Radiation, Pacific-North American pattern, Pacific Decadal Oscillation, Southern Oscillation Index, and sea surface temperatures. We compare the performance of linear regression with several machine learning algorithms, such as random forest, gradient boosting, extremely randomized trees, and extreme gradient boosting. Our results show that including climate-related variables improves predictive accuracy across all models, with extremely randomized trees achieving the lowest root mean squared error (RMSE). These findings suggest that large-scale climate variability has a measurable influence on CAT bond pricing and that machine learning methods can effectively capture these complex relationships.
2512.22660Dec 2025
View
Almost-Exact Simulation Scheme for Heston-type Models: Bermudan and American Option Pricing
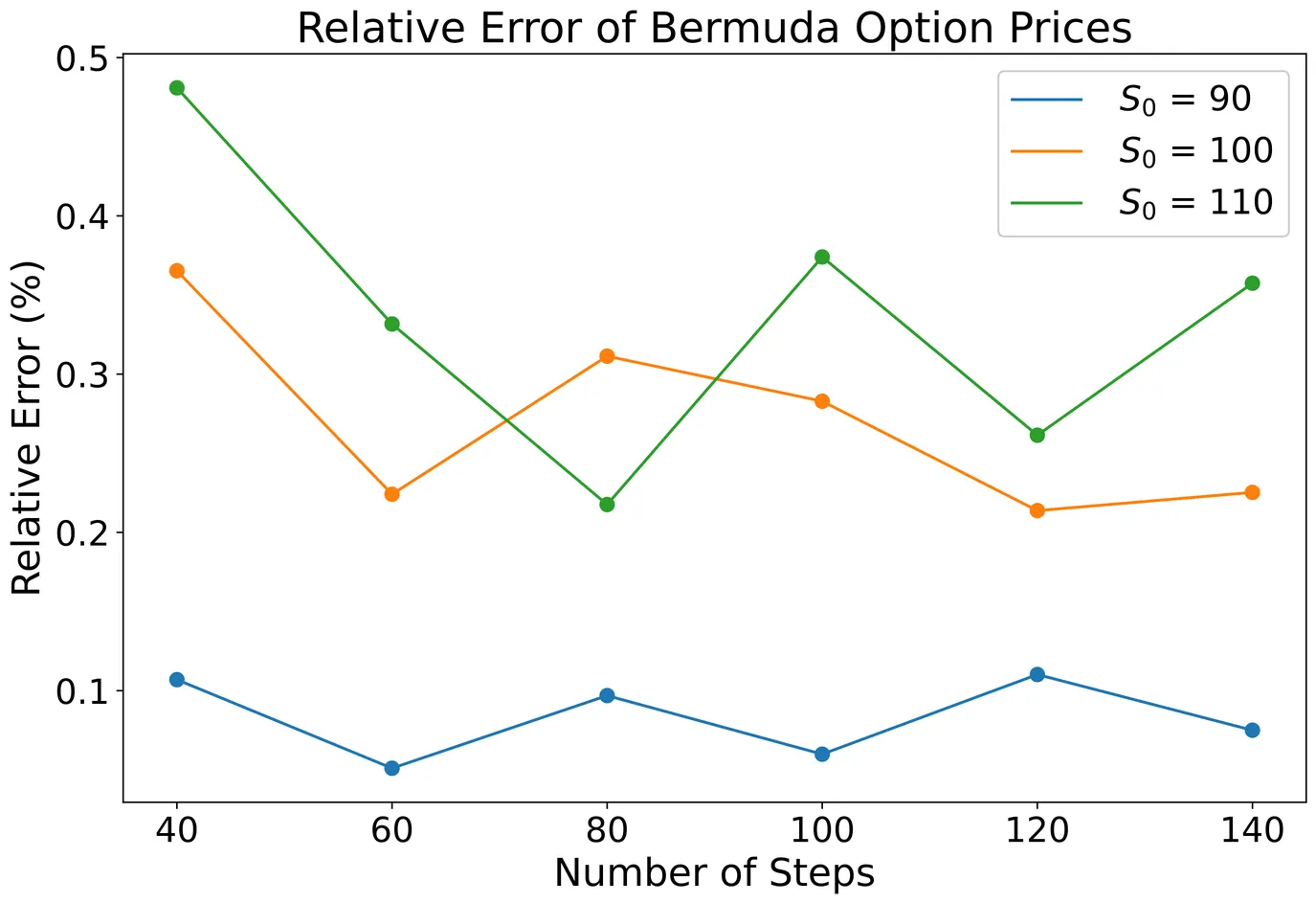
Recently, an Almost-Exact Simulation (AES) scheme was introduced for the Heston stochastic volatility model and tested for European option pricing. This paper extends this scheme for pricing Bermudan and American options under both Heston and double Heston models. The AES improves Monte Carlo simulation efficiency by using the non-central chi-square distribution for the variance process. We derive the AES scheme for the double Heston model and compare the performance of the AES schemes under both models with the Euler scheme. Our numerical experiments validate the effectiveness of the AES scheme in providing accurate option prices with reduced computational time, highlighting its robustness for both models. In particular, the AES achieves higher accuracy and computational efficiency when the number of simulation steps matches the exercise dates for Bermudan options.
2601.00815Dec 2025
View
Interpretable Deep Learning for Stock Returns: A Consensus-Bottleneck Asset Pricing Model
We introduce the \textit{Consensus-Bottleneck Asset Pricing Model} (CB-APM), a partially interpretable neural network that replicates the reasoning processes of sell-side analysts by capturing how dispersed investor beliefs are compressed into asset prices through a consensus formation process. By modeling this ``bottleneck'' to summarize firm- and macro-level information, CB-APM not only predicts future risk premiums of U.S. equities but also links belief aggregation to expected returns in a structurally interpretable manner. The model improves long-horizon return forecasts and outperforms standard deep learning approaches in both predictive accuracy and explanatory power. Comprehensive portfolio analyses show that CB-APM's out-of-sample predictions translate into economically meaningful payoffs, with monotonic return differentials and stable long-short performance across regularization settings. Empirically, CB-APM leverages consensus as a regularizer to amplify long-horizon predictability and yields interpretable consensus-based components that clarify how information is priced in returns. Moreover, regression and GRS-based pricing diagnostics reveal that the learned consensus representations capture priced variation only partially spanned by traditional factor models, demonstrating that CB-APM uncovers belief-driven structure in expected returns beyond the canonical factor space. Overall, CB-APM provides an interpretable and empirically grounded framework for understanding belief-driven return dynamics.
2512.16251Dec 2025
View
Semi-analytical pricing of American options with hybrid dividends via integral equations and the GIT method
This paper introduces a semi-analytical method for pricing American options on assets (stocks, ETFs) that pay discrete and/or continuous dividends. The problem is notoriously complex because discrete dividends create abrupt price drops and affect the optimal exercise timing, making traditional continuous-dividend models unsuitable. Our approach utilizes the Generalized Integral Transform (GIT) method introduced by the author and his co-authors in a number of papers, which transforms the pricing problem from a complex partial differential equation with a free boundary into an integral Volterra equation of the second or first kind. In this paper we illustrate this approach by considering a popular GBM model that accounts for discrete cash and proportional dividends using Dirac delta functions. By reframing the problem as an integral equation, we can sequentially solve for the option price and the early exercise boundary, effectively handling the discontinuities caused by the dividends. Our methodology provides a powerful alternative to standard numerical techniques like binomial trees or finite difference methods, which can struggle with the jump conditions of discrete dividends by losing accuracy or performance. Several examples demonstrate that the GIT method is highly accurate and computationally efficient, bypassing the need for extensive computational grids or complex backward induction steps.
2510.18159Oct 2025
View
Berms without Calibration
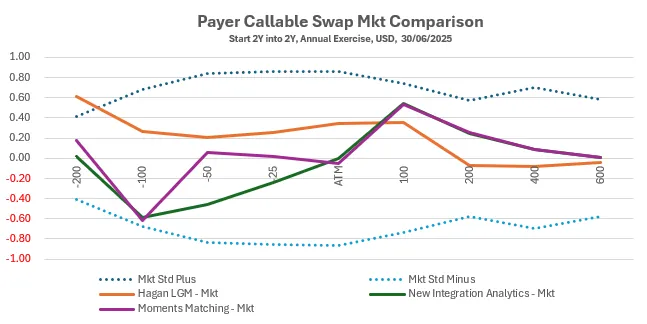
A new semi-analytical pricing model for Bermudan swaptions based on swap rates distributions and correlations between them. The model does not require product specific calibration.
2510.15984Oct 2025
View
Quantum-Theoretical Re-interpretation of Pricing Theory
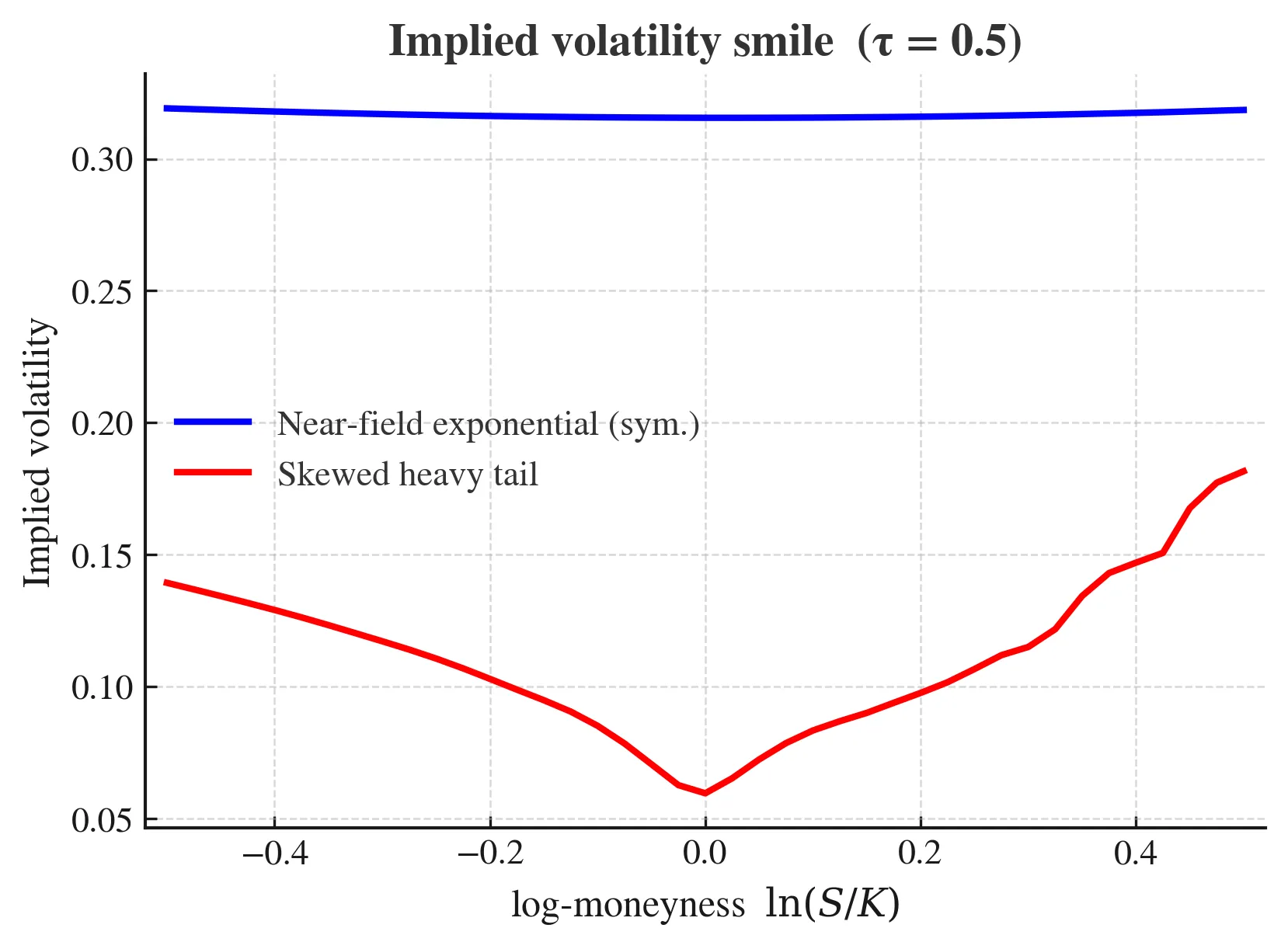
Motivated by Heisenberg's observable-only stance, we replace latent "information" (filtrations, hidden diffusions, state variables) with observable transitions between price states. On a discrete price lattice with a Hilbert-space representation, shift operators and the spectral calculus of the price define observable frequency operators and a translation-invariant convolution generator. Combined with jump operators that encode transition intensities, this yields a completely positive, translation-covariant Lindblad semigroup. Under the risk-neutral condition the framework leads to a nonlocal pricing equation that is diagonal in Fourier space; in the small-mesh diffusive limit its generator converges to the classical Black-Scholes-Merton operator. We do not propose another parametric model. We propose a foundation for model construction that is observable, first-principles, and mathematically natural. Noncommutativity emerges from the observable shift algebra rather than being postulated. The jump-intensity ledger determines tail behavior and short-maturity smiles and implies testable links between extreme-event probabilities and implied-volatility wings. Future directions: (i) multi-asset systems on higher-dimensional lattices with vector shifts and block kernels; (ii) state- or flow-dependent kernels as "financial interactions" leading to nonlinear master equations while preserving linear risk-neutral pricing; (iii) empirical tests of the predicted scaling relations between jump intensities and market extremes.
2510.06287Oct 2025
View
2506.08067Smile asymptotic for Bachelier Implied Volatility
We investigate the asymptotic behaviour of the Implied Volatility in the Bachelier setting, extending the framework introduced by Benaim and Friz for the Black-Scholes setting. Exploiting the theory of regular variation, we derive explicit expressions for the Bachelier Implied Volatility in the wings of the smile, linking these to the tail behaviour of the underlying's returns' distribution. Furthermore, we establish a direct connection between the analyticity strip of the returns' characteristic function and the asymptotic formula for the Implied Volatility smile at extreme moneyness.
2506.08067Jun 2025
View
Multi-Task Dynamic Pricing in Credit Market with Contextual Information
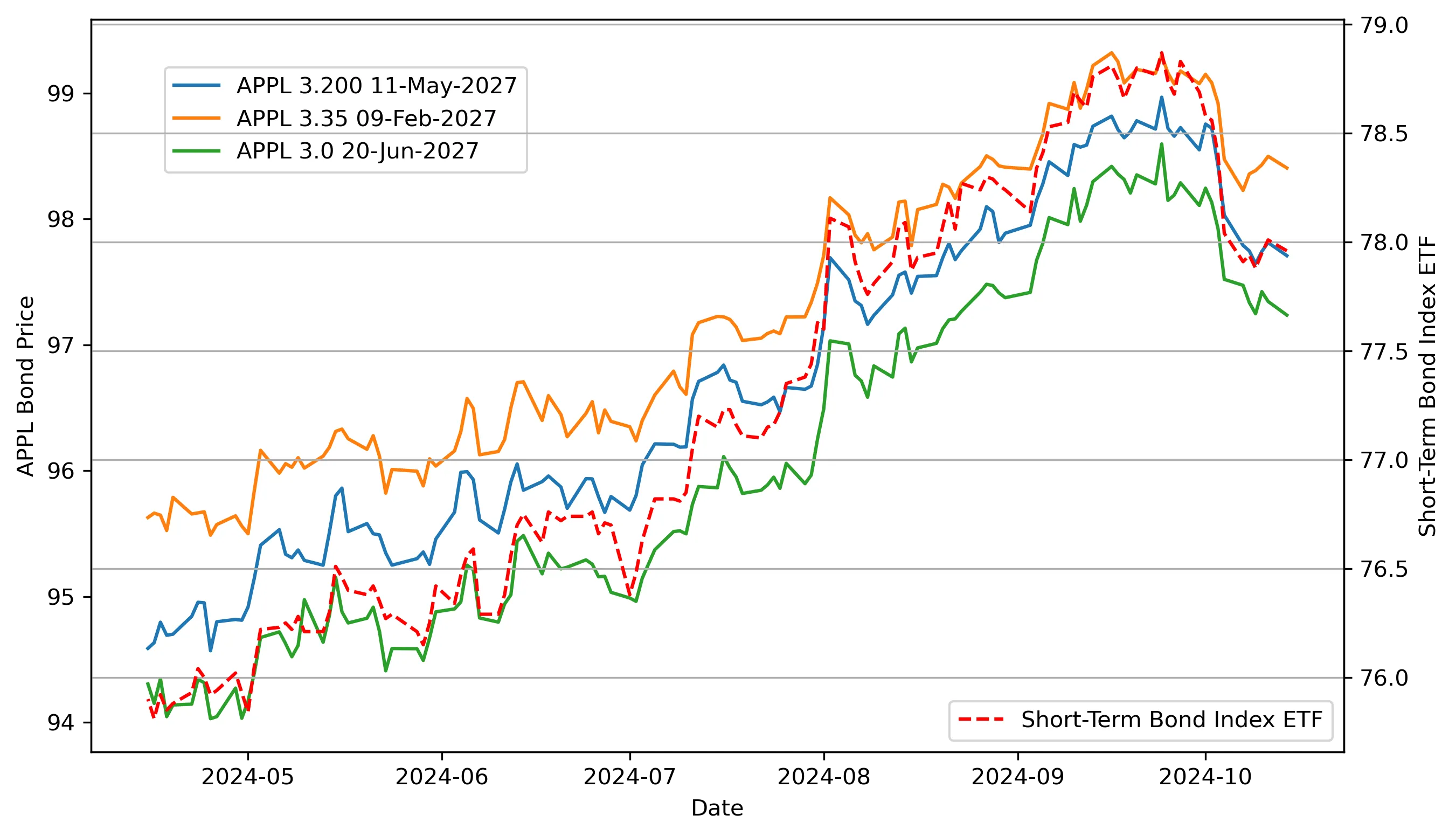
We study the dynamic pricing problem faced by a broker seeking to learn prices for a large number of credit market securities, such as corporate bonds, government bonds, loans, and other credit-related securities. A major challenge in pricing these securities stems from their infrequent trading and the lack of transparency in over-the-counter (OTC) markets, which leads to insufficient data for individual pricing. Nevertheless, many securities share structural similarities that can be exploited. Moreover, brokers often place small "probing" orders to infer competitors' pricing behavior. Leveraging these insights, we propose a multi-task dynamic pricing framework that leverages the shared structure across securities to enhance pricing accuracy. In the OTC market, a broker wins a quote by offering a more competitive price than rivals. The broker's goal is to learn winning prices while minimizing expected regret against a clairvoyant benchmark. We model each security using a $d$-dimensional feature vector and assume a linear contextual model for the competitor's pricing of the yield, with parameters unknown a priori. We propose the Two-Stage Multi-Task (TSMT) algorithm: first, an unregularized MLE over pooled data to obtain a coarse parameter estimate; second, a regularized MLE on individual securities to refine the parameters. We show that the TSMT achieves a regret bounded by $\tilde{O} ( δ_{\max} \sqrt{T M d} + M d ) $, outperforming both fully individual and fully pooled baselines, where $M$ is the number of securities and $δ_{\max}$ quantifies their heterogeneity.
2410.148391Oct 2024
View1012.1037Pricing of barrier options by marginal functional quantization
This paper is devoted to the pricing of Barrier options by optimal quadratic quantization method. From a known useful representation of the premium of barrier options one deduces an algorithm similar to one used to estimate nonlinear filter using quadratic optimal functional quantization. Some numerical tests are fulfilled in the Black-Scholes model and in a local volatility model and a comparison to the so called Brownian Bridge method is also done.
1012.103716Dec 2010
View