Data Analysis, Statistics and Probability
Methods, software and hardware for physics data analysis.
Methods, software and hardware for physics data analysis.
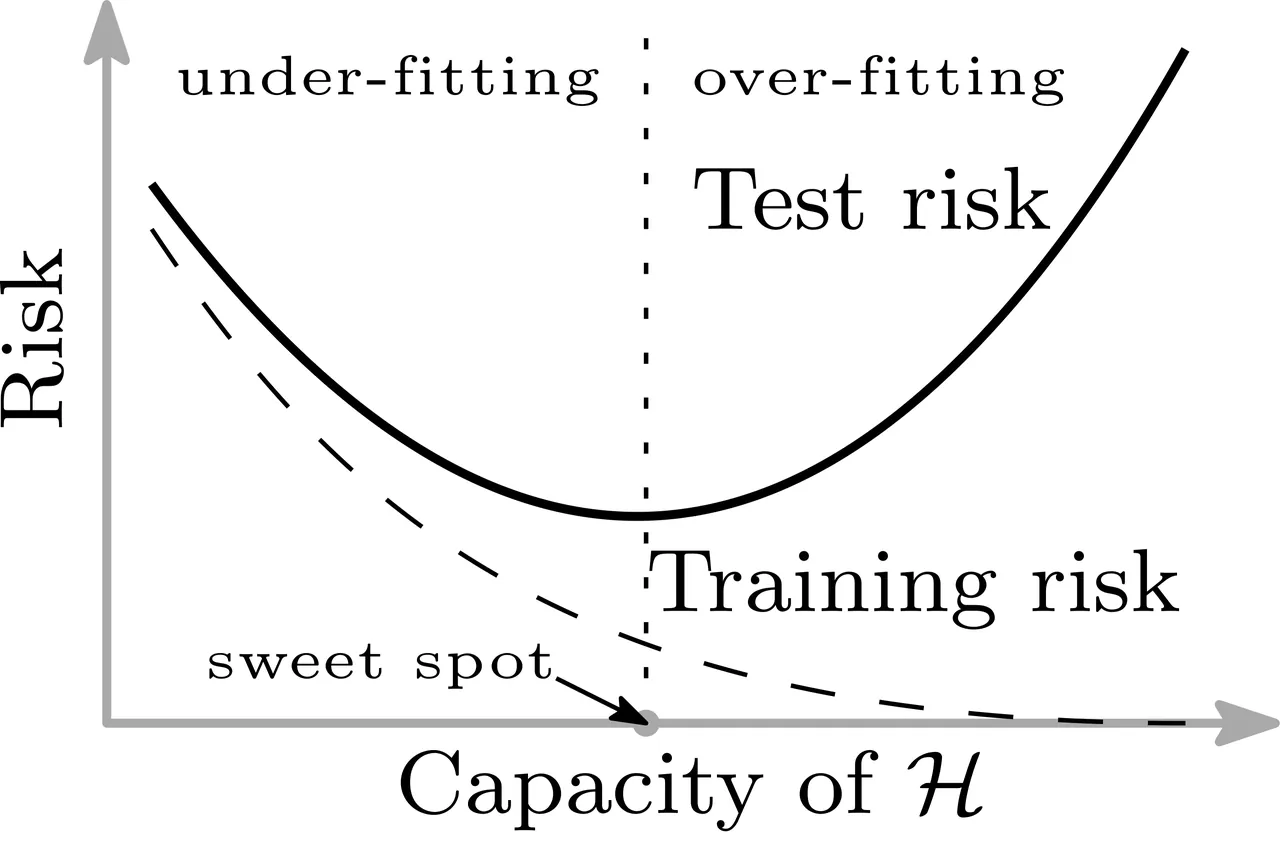
This chapter gives an overview of the core concepts of machine learning (ML) -- the use of algorithms that learn from data, identify patterns, and make predictions or decisions without being explicitly programmed -- that are relevant to particle physics with some examples of applications to the energy, intensity, cosmic, and accelerator frontiers.
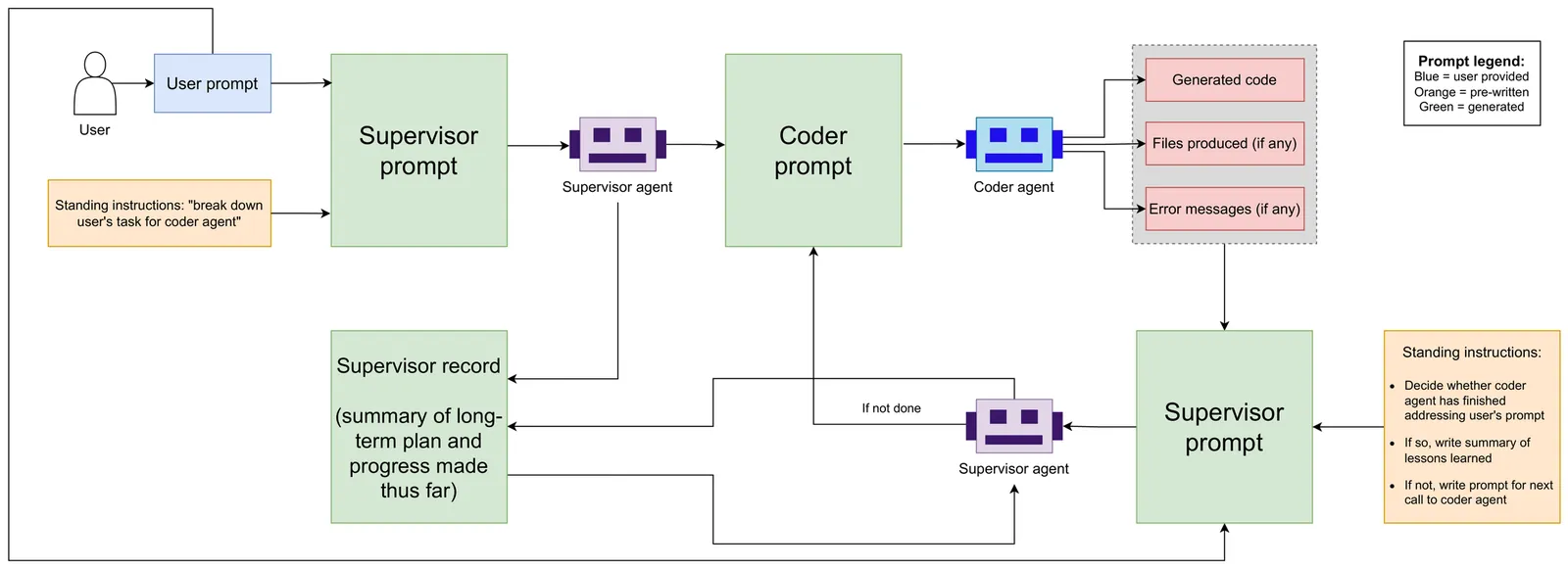
We present a proof-of-principle study demonstrating the use of large language model (LLM) agents to automate a representative high energy physics (HEP) analysis. Using the Higgs boson diphoton cross-section measurement as a case study with ATLAS Open Data, we design a hybrid system that combines an LLM-based supervisor-coder agent with the Snakemake workflow manager. In this architecture, the workflow manager enforces reproducibility and determinism, while the agent autonomously generates, executes, and iteratively corrects analysis code in response to user instructions. We define quantitative evaluation metrics including success rate, error distribution, costs per specific task, and average number of API calls, to assess agent performance across multi-stage workflows. To characterize variability across architectures, we benchmark a representative selection of state-of-the-art LLMs spanning the Gemini and GPT-5 series, the Claude family, and leading open-weight models. While the workflow manager ensures deterministic execution of all analysis steps, the final outputs still show stochastic variation. Although we set the temperature to zero, other sampling parameters (e.g., top-p, top-k) remained at their defaults, and some reasoning-oriented models internally adjust these settings. Consequently, the models do not produce fully deterministic results. This study establishes the first LLM-agent-driven automated data-analysis framework in HEP, enabling systematic benchmarking of model capabilities, stability, and limitations in real-world scientific computing environments. The baseline code used in this work is available at https://huggingface.co/HWresearch/LLM4HEP. This work was accepted as a poster at the Machine Learning and the Physical Sciences (ML4PS) workshop at NeurIPS 2025. The initial submission was made on August 30, 2025.
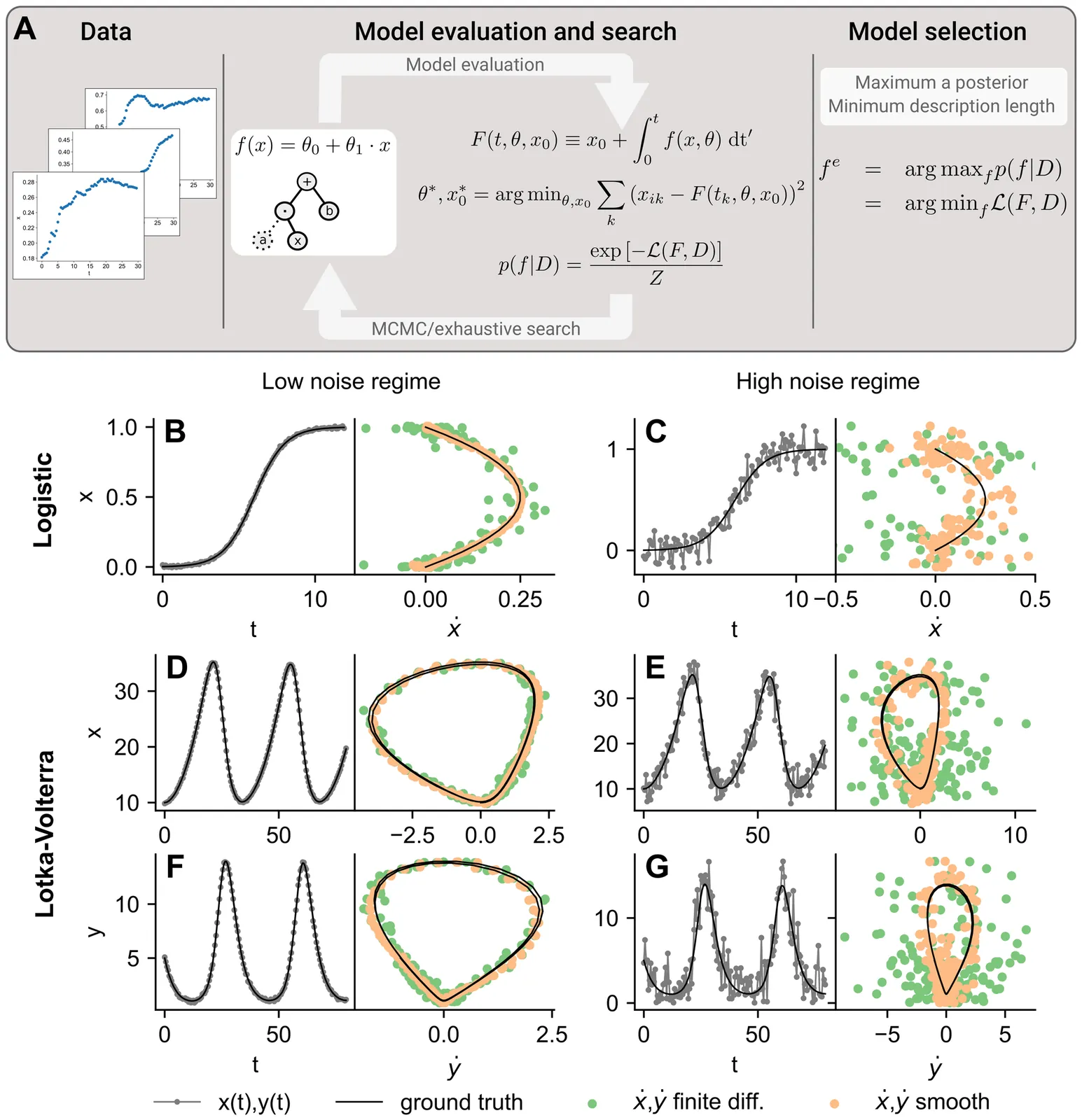
Understanding how systems evolve over time often requires discovering the differential equations that govern their behavior. Automatically learning these equations from experimental data is challenging when the data are noisy or limited, and existing approaches struggle, in particular, with the estimation of unobserved derivatives. Here, we introduce an integral Bayesian symbolic regression method that learns governing equations directly from raw time-series data, without requiring manual assumptions or error-prone derivative estimation. By sampling the space of symbolic differential equations and evaluating them via numerical integration, our method robustly identifies governing equations even from noisy or scarce data. We show that this approach accurately recovers ground-truth models in synthetic benchmarks, and that it makes quasi-optimal predictions of system dynamics for all noise regimes. Applying this method to bacterial growth experiments across multiple species and substrates, we discover novel growth equations that outperform classical models in accurately capturing all phases of microbial proliferation, including lag, exponential, and saturation. Unlike standard approaches, our method reveals subtle shifts in growth dynamics, such as double ramp-ups or non-canonical transitions, offering a deeper, data-driven understanding of microbial physiology.
Quantifying numerical data involves addressing two key challenges: first, determining whether the data can be naturally quantified, and second, identifying the numerical intervals or ranges of values that correspond to specific value classes, referred to as "quantums," which represent statistically meaningful states. If such quantification is feasible, continuous streams of numerical data can be transformed into sequences of "symbols" that reflect the states of the system described by the measured parameter. People often perform this task intuitively, relying on common sense or practical experience, while information theory and computer science offer computable metrics for this purpose. In this study, we assess the applicability of metrics based on information compression and the Silhouette coefficient for quantifying numerical data. We also investigate the extent to which these metrics correlate with one another and with what is commonly referred to as "human intuition." Our findings suggest that the ability to classify numeric data values into distinct categories is associated with a Silhouette coefficient above 0.65 and a Dip Test below 0.5; otherwise, the data can be treated as following a unimodal normal distribution. Furthermore, when quantification is possible, the Silhouette coefficient appears to align more closely with human intuition than the "normalized centroid distance" method derived from information compression perspective.
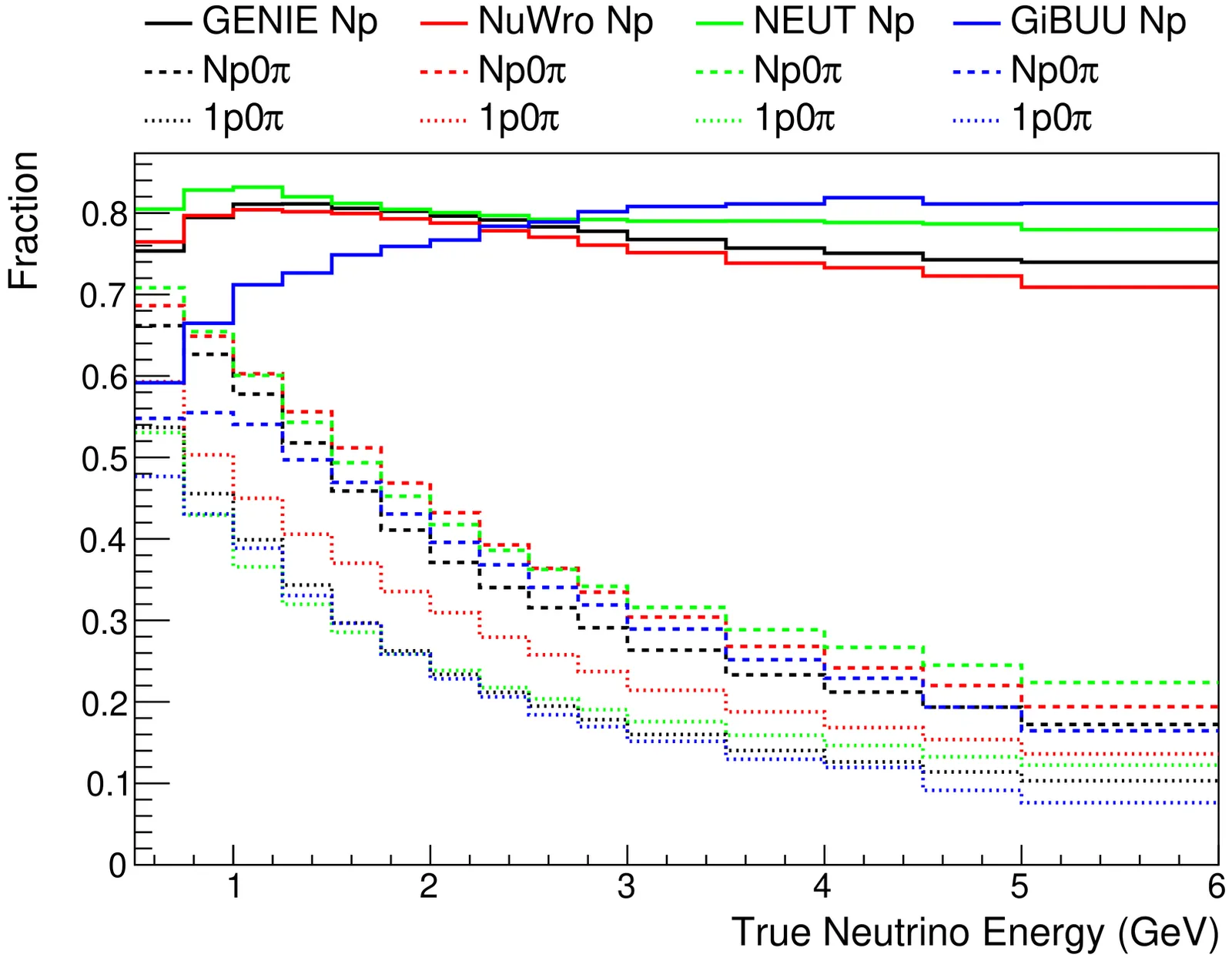
Accurate determination of the neutrino energy is central to precision oscillation measurements. In this work, we introduce the W$^2$-based estimator, a new neutrino energy estimator based on the measurement of the final-state hadronic invatiant mass. This estimator is particularly designed to be employed in liquid-argon time-projection chambers exposed to broadband beams that span the challenging transition region between shallow inelastic scattering and deep inelastic scattering. The performance of the W$^2$-based estimator is compared against four other commonly used estimators. The impact of the estimator choice is evaluated by performing measurements of $δ_{CP}$ and $Δm^2_{23}$ in a toy long-baseline oscillation analysis. We find that the W$^2$-based estimator shows the smallest bias as a funciton of true neutrino energy and it is particularly stable against the mismodelling of lepton scattering angle, missing energy, hadronic invariant mass and final state interactions. Such an inclusive channel complements well the strength of more exclusive methods that optimizes the energy resolution. By providing a detailed analysis of strengths, weaknesses and domain of applicability of each estimator, this work informs the combined used of energy estimators in any future LArTPC-based oscillation analysis.
 2510.25162
2510.25162Robert Cousins has posted a comment on my manuscript on ``Confidence intervals for the Poisson distribution''. His key point is that one should not include in the likelihood non-physical parameter values, even for frequency statistics. This is my response, in which I contend that it can be useful to do so when discussing such descriptive statistics.
Understanding the temporal dependence of precipitation is key to improving weather predictability and developing efficient stochastic rainfall models. We introduce an information-theoretic approach to quantify memory effects in discrete stochastic processes and apply it to daily precipitation records across the contiguous United States. The method is based on the predictability gain, a quantity derived from block entropy that measures the additional information provided by higher-order temporal dependencies. This statistic, combined with a bootstrap-based hypothesis testing and Fisher's method, enables a robust memory estimator from finite data. Tests with generated sequences show that this estimator outperforms other model-selection criteria such as AIC and BIC. Applied to precipitation data, the analysis reveals that daily rainfall occurrence is well described by low-order Markov chains, exhibiting regional and seasonal variations, with stronger correlations in winter along the West Coast and in summer in the Southeast, consistent with known climatological patterns. Overall, our findings establish a framework for building parsimonious stochastic descriptions, useful when addressing spatial heterogeneity in the memory structure of precipitation dynamics, and support further advances in real-time, data-driven forecasting schemes.
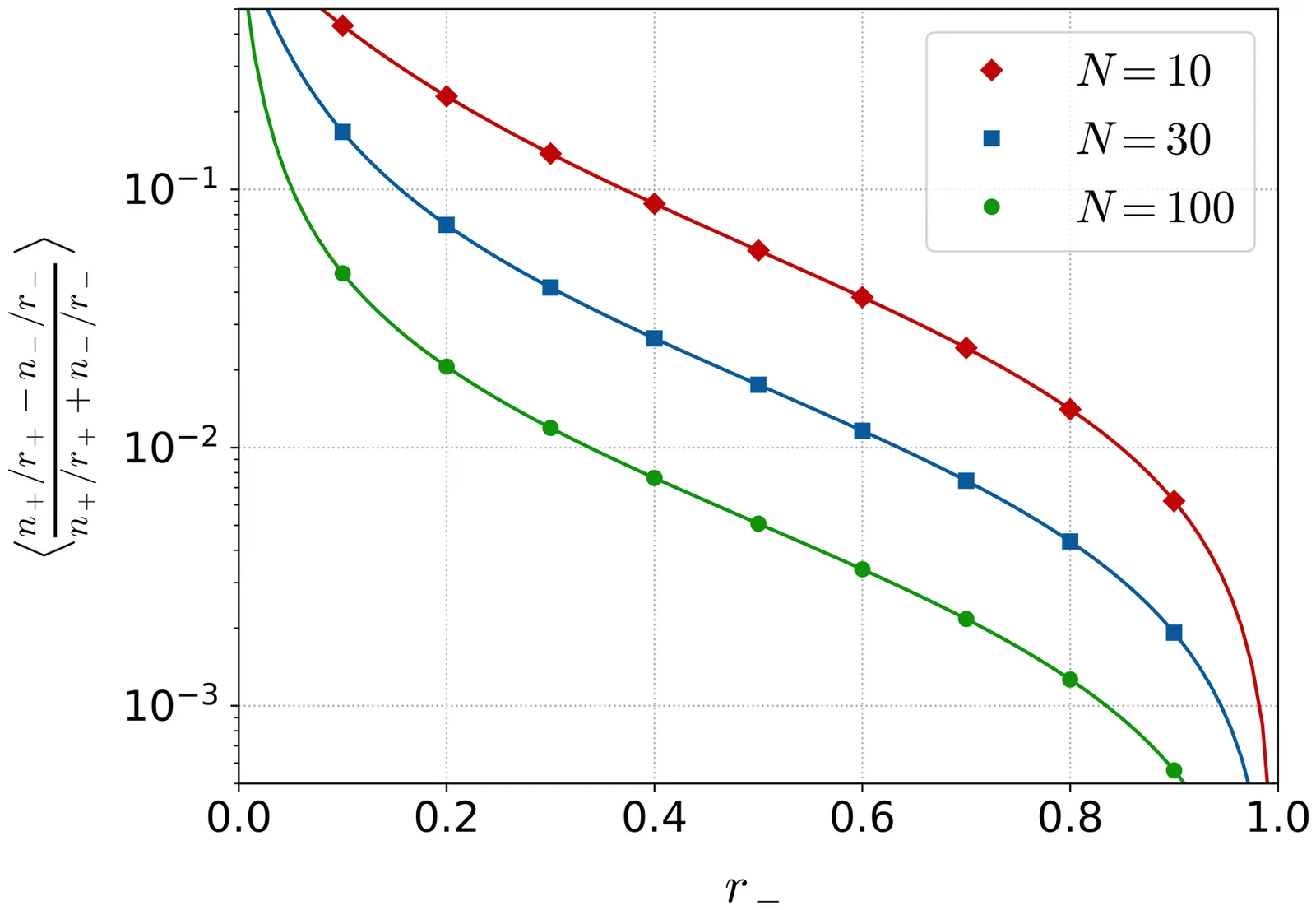
We derive analytic formulas to reconstruct particle-averaged quantities from experimental results that suffer from the efficiency loss of particle measurements. These formulas are derived under the assumption that the probabilities of observing individual particles are independent. The formulas do not agree with the conventionally used intuitive formulas.
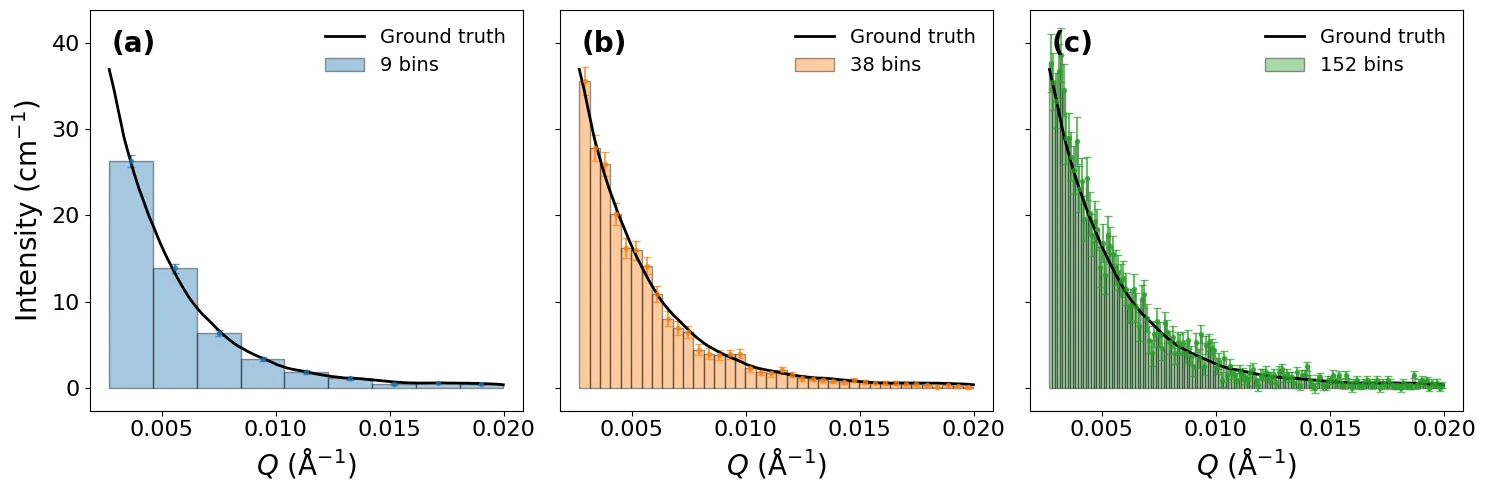
Small-Angle Neutron Scattering (SANS) data analysis often relies on fixed-width binning schemes that overlook variations in signal strength and structural complexity. We introduce a statistically grounded approach based on the Freedman-Diaconis (FD) rule, which minimizes the mean integrated squared error between the histogram estimate and the true intensity distribution. By deriving the competing scaling relations for counting noise ($\propto h^{-1}$) and binning distortion ($\propto h^{2}$), we establish an optimal bin width that balances statistical precision and structural resolution. Application to synthetic data from the Debye scattering function of a Gaussian polymer chain demonstrates that the FD criterion quantitatively determines the most efficient binning, faithfully reproducing the curvature of $I(Q)$ while minimizing random error. The optimal width follows the expected scaling $h_{\mathrm{opt}} \propto N_{\mathrm{total}}^{-1/3}$, delineating the transition between noise- and resolution-limited regimes. This framework provides a unified, physics-informed basis for adaptive, statistically efficient binning in neutron scattering experiments.
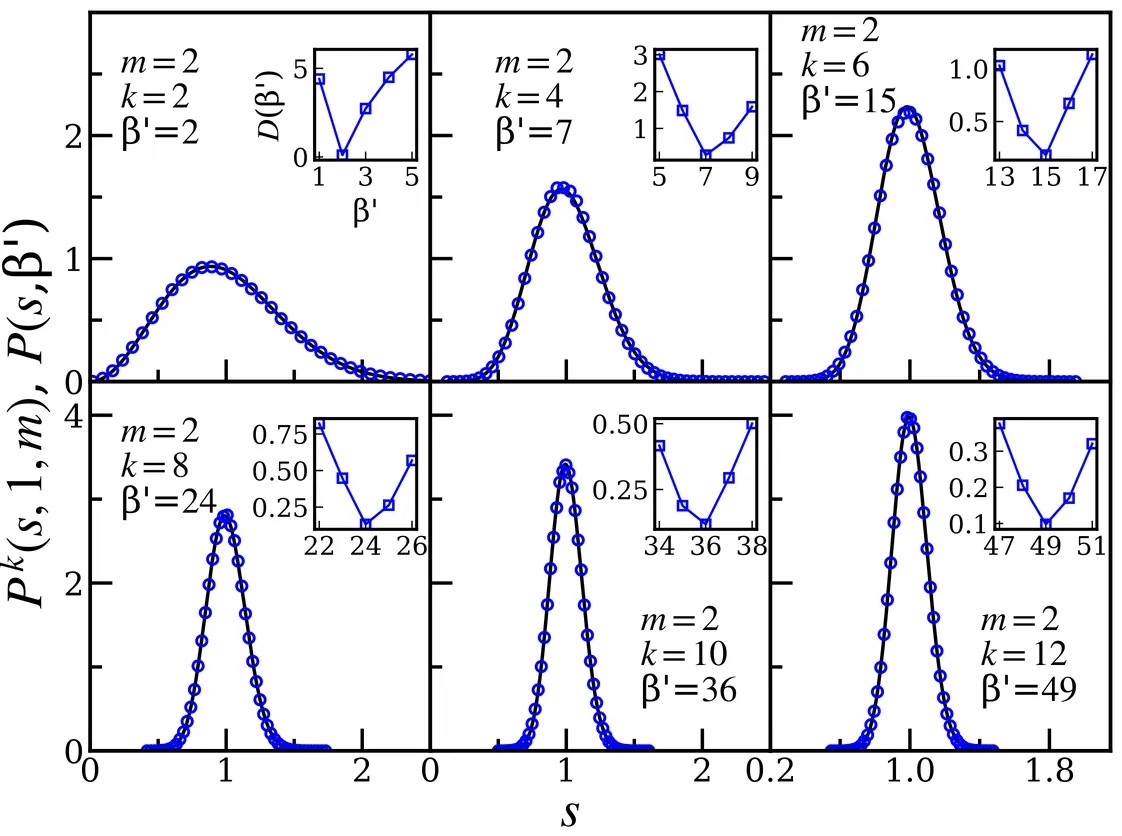
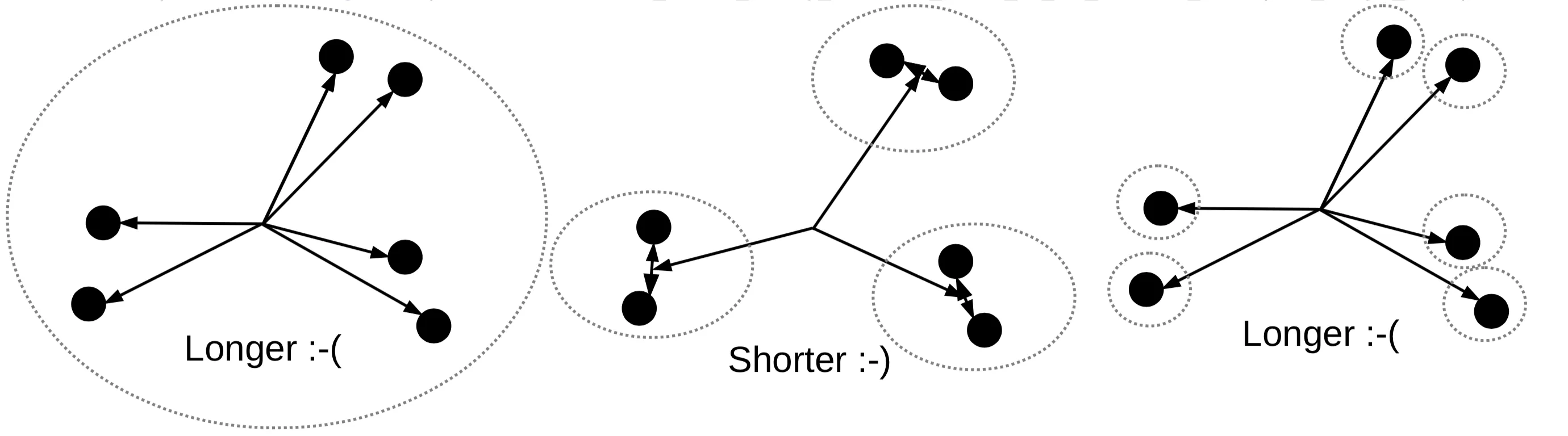
The connection between random matrices and the spectral fluctuations of complex quantum systems in a suitable limit can be explained by using the setup of random matrix theory. Higher-order spacing statistics in the $m$ superposed spectra of circular random matrices are studied numerically. We tabulated the modified Dyson index $β'$ for a given $m$, $k$, and $β$, for which the nearest neighbor spacing distribution is the same as that of the $k$-th order spacing distribution corresponding to the $β$ and $m$. Here, we conjecture that for given $m(k)$ and $β$, the obtained sequence of $β'$ as a function of $k(m)$ is unique. This result can be used as a tool for the characterization of the system and to determine the symmetry structure of the system without desymmetrization of the spectra. We verify the results of the $m=2$ case of COE with the quantum kicked top model corresponding to various Hilbert space dimensions. From the comparative study of the higher-order spacings and ratios in both $m=1$ and $m=2$ cases of COE and GOE by varying dimension, keeping the number of realizations constant and vice-versa, we find that both COE and GOE have the same asymptotic behavior in terms of a given higher-order statistics. But, we found from our numerical study that within a given ensemble of COE or GOE, the results of spacings and ratios agree with each other only up to some lower $k$, and beyond that, they start deviating from each other. It is observed that for the $k=1$ case, the convergence towards the Poisson distribution is faster in the case of ratios than the corresponding spacings as we increase $m$ for a given $β$. Further, the spectral fluctuations of the intermediate map of various dimensions are studied. There, we find that the effect of random numbers used to generate the matrix corresponding to the map is reflected in the higher-order statistics.
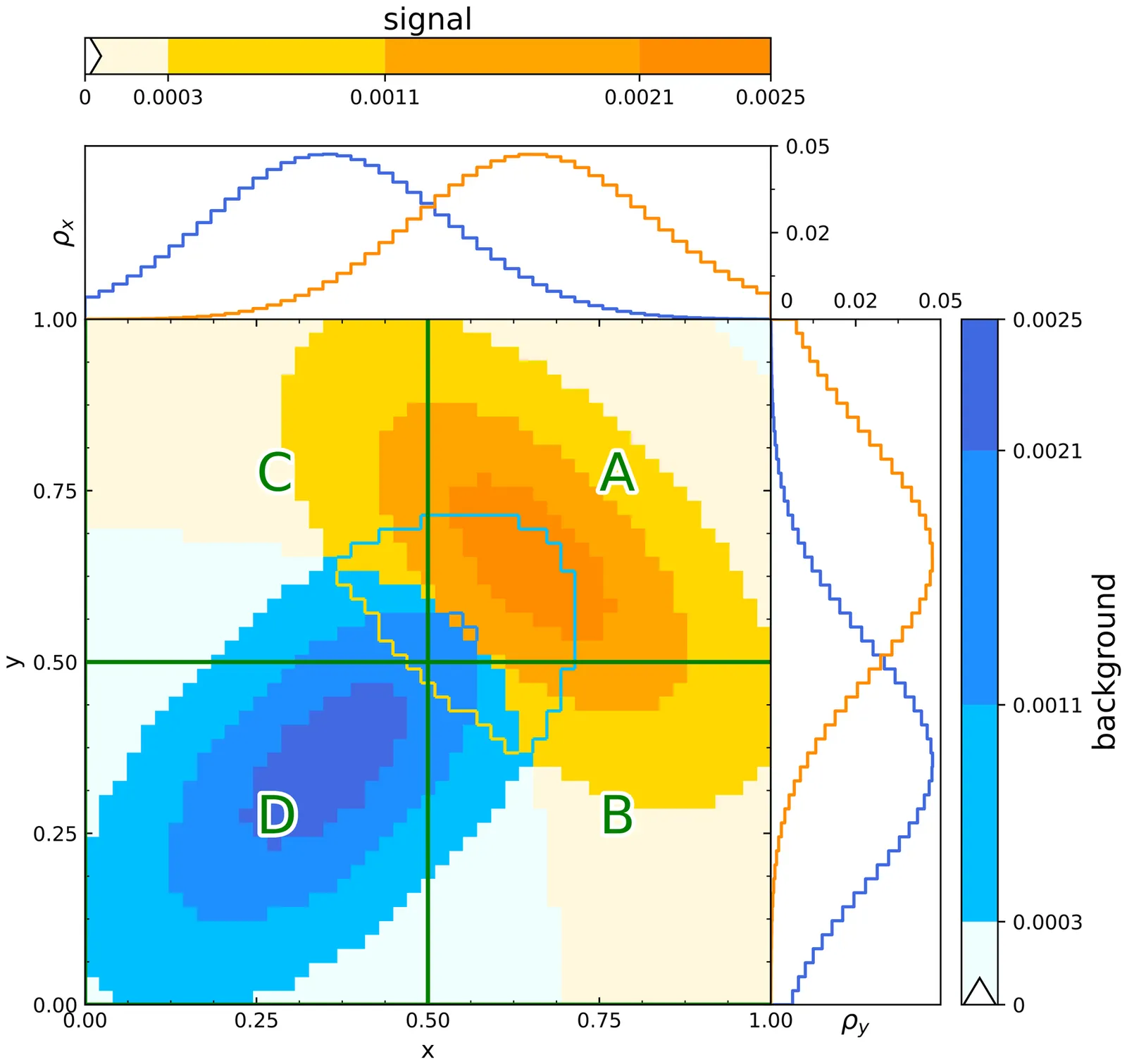
A novel numerical technique is presented to transform one random variable within a system toward statistical quasi-independence from any other random variable in the system. The method's applicability is demonstrated through a particle physics example where a classifier is rendered quasi-independent from an observable quantity.
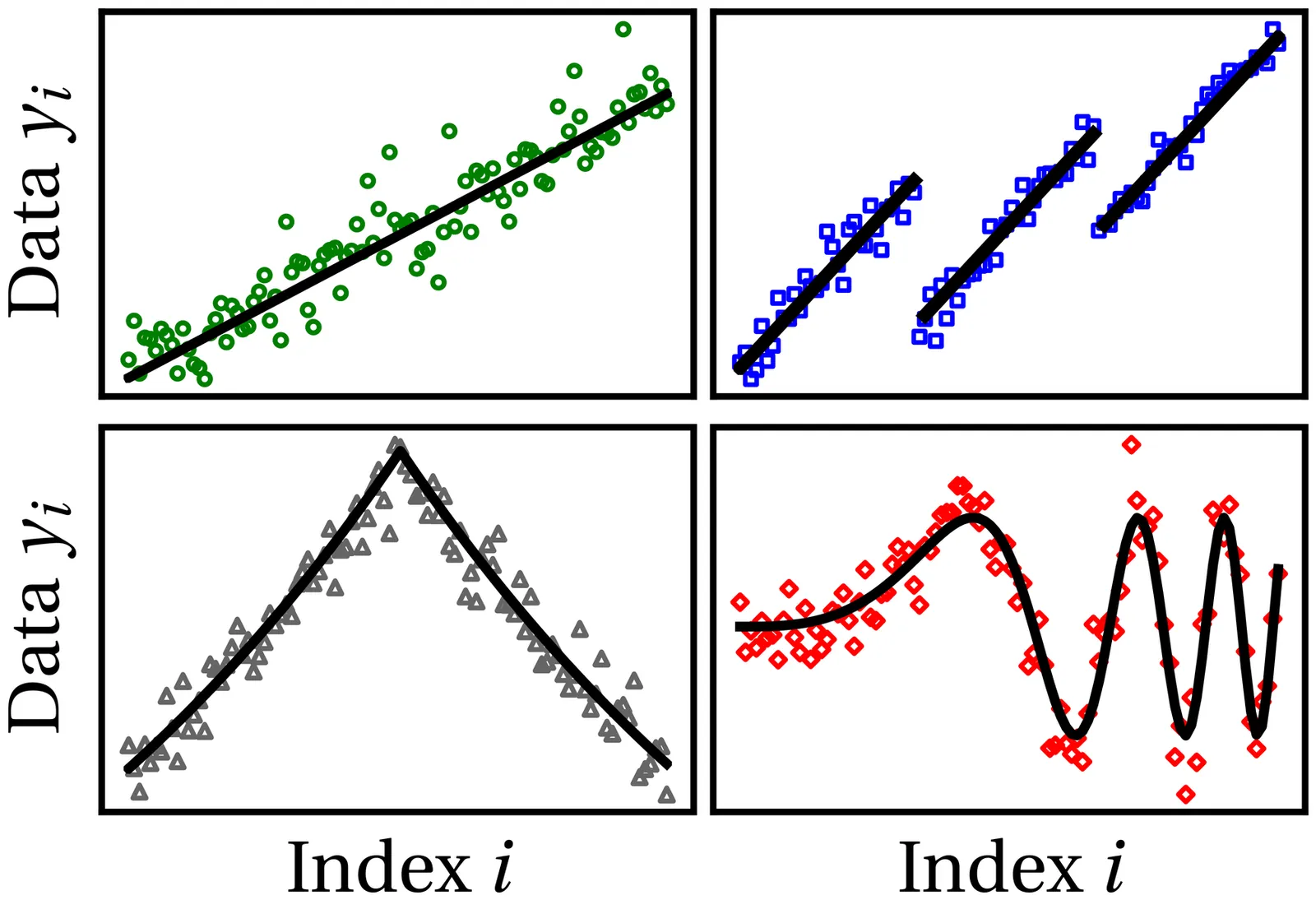
A frequently occurring challenge in experimental and numerical observation is how to resolve features, such as spectral peaks - with center, width, height - and derivatives from measured data with unavoidable noise. Therefore, we develop a modified Whittaker-Henderson smoothing procedure that balances the spectral features and the noise. In our procedure, we introduce adjustable weights that are optimized using cross-validation. When the measurement errors are known, a straightforward error analysis of the smoothed results is feasible. As an example, we calculate the optical group delay dispersion of a Bragg reflector from synthetic phase data with noise to illustrate the effectiveness of the smoothing algorithm. The smoother faithfully reconstructs the group delay dispersion, allowing to observe details that otherwise remain buried in noise. To further illustrate the power of our smoother, we study several commonly occurring difficulties in data and data analysis and show how to properly smoothen unequally sampled data, how to obtain discontinuities, including discontinuous derivatives or kinks, and how to properly smooth data in the vicinity of boundaries to the domains.
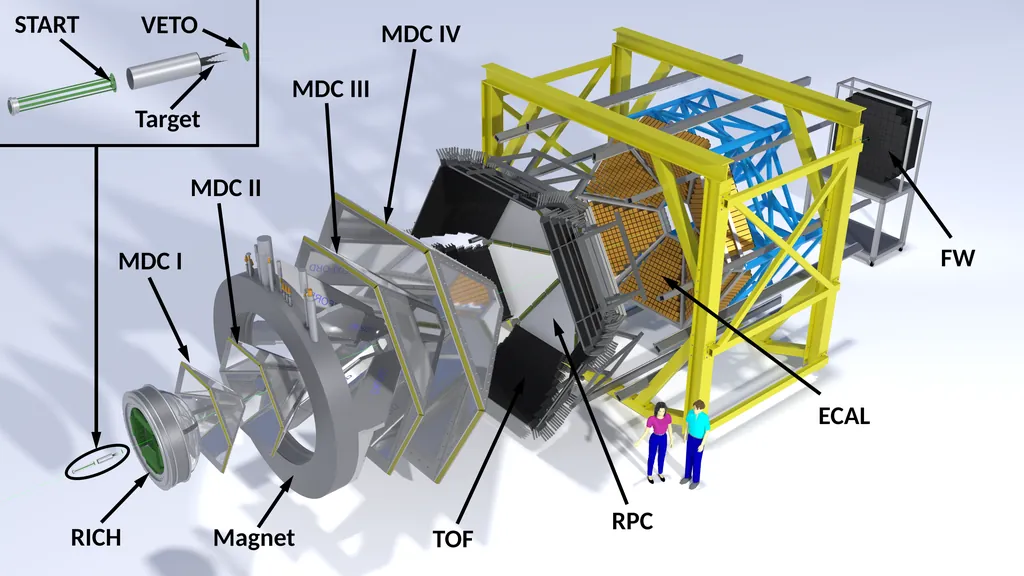
In experimental nuclear and particle physics, the extraction of high-purity samples of rare events critically depends on the efficiency and accuracy of particle identification (PID). In this work, we present a PID method applied to HADES data at the level of fully reconstructed particle track candidates. The results demonstrate a significant improvement in PID performance compared to conventional techniques, highlighting the potential of physics-informed neural networks as a powerful tool for future data analyses.
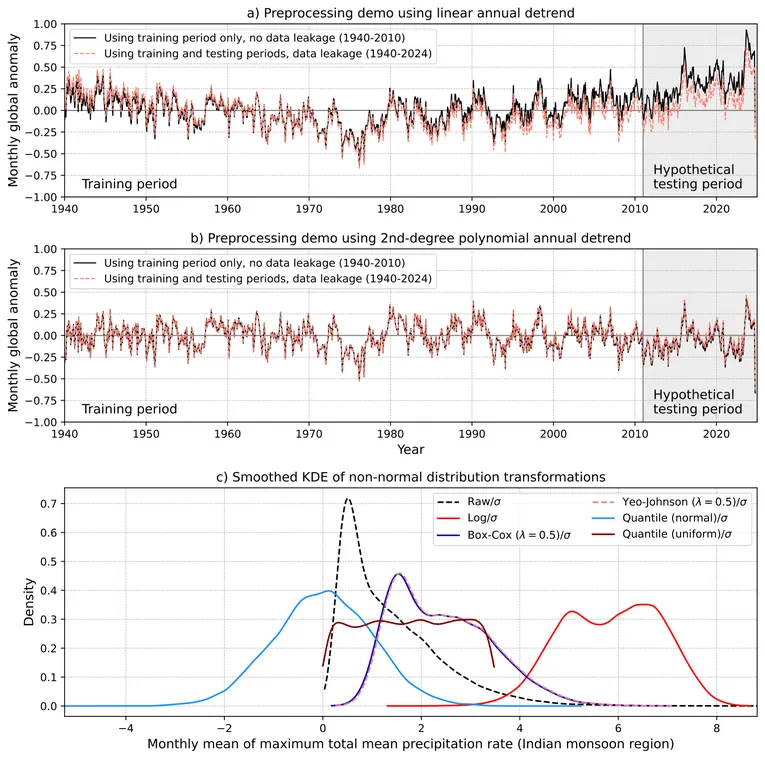
Artificial intelligence (AI) - and specifically machine learning (ML) - applications for climate prediction across timescales are proliferating quickly. The emergence of these methods prompts a revisit to the impact of data preprocessing, a topic familiar to the climate community, as more traditional statistical models work with relatively small sample sizes. Indeed, the skill and confidence in the forecasts produced by data-driven models are directly influenced by the quality of the datasets and how they are treated during model development, thus yielding the colloquialism, "garbage in, garbage out." As such, this article establishes protocols for the proper preprocessing of input data for AI/ML models designed for climate prediction (i.e., subseasonal to decadal and longer). The three aims are to: (1) educate researchers, developers, and end users on the effects that preprocessing has on climate predictions; (2) provide recommended practices for data preprocessing for such applications; and (3) empower end users to decipher whether the models they are using are properly designed for their objectives. Specific topics covered in this article include the creation of (standardized) anomalies, dealing with non-stationarity and the spatiotemporally correlated nature of climate data, and handling of extreme values and variables with potentially complex distributions. Case studies will illustrate how using different preprocessing techniques can produce different predictions from the same model, which can create confusion and decrease confidence in the overall process. Ultimately, implementing the recommended practices set forth in this article will enhance the robustness and transparency of AI/ML in climate prediction studies.
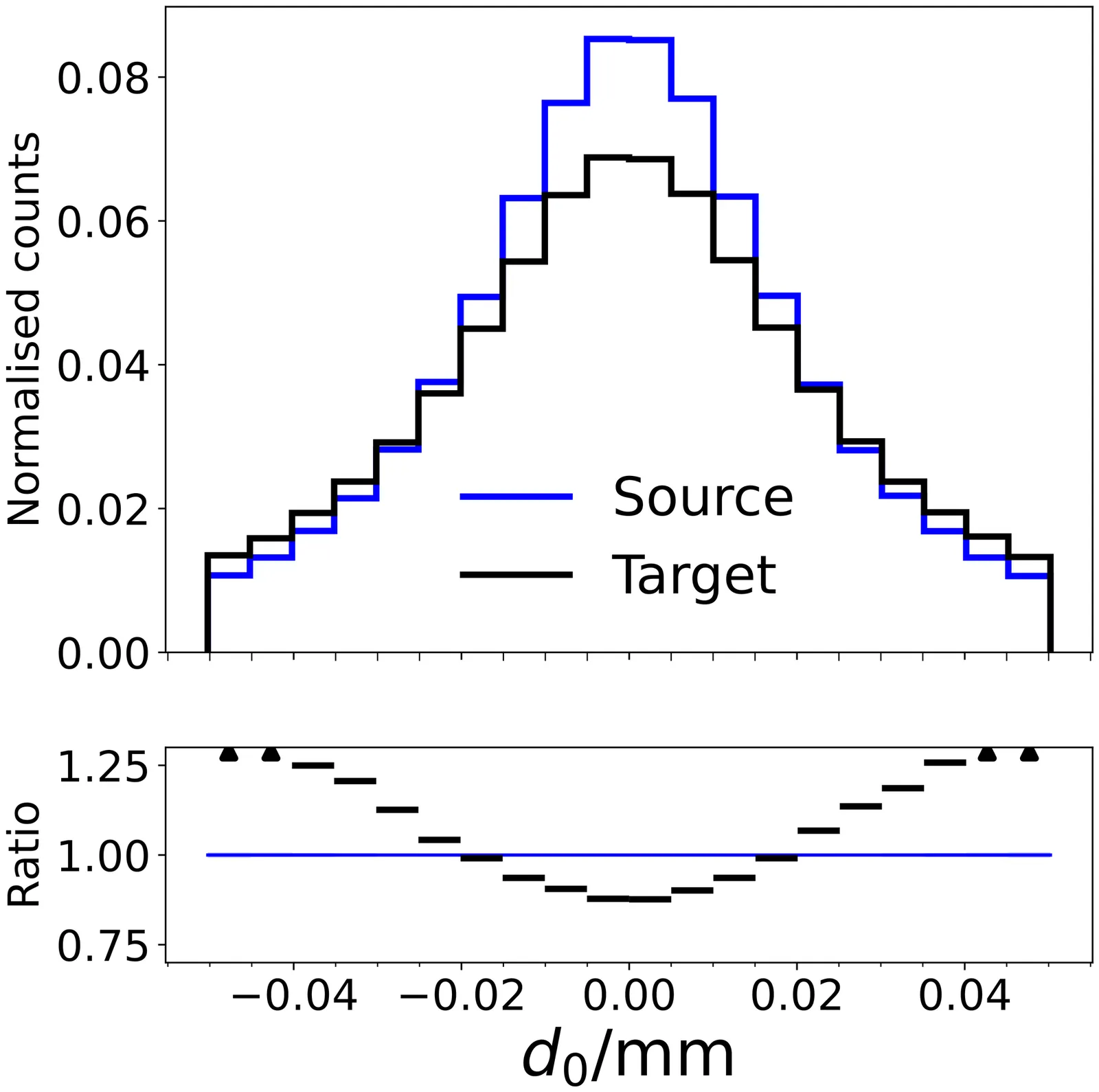
Machine learning (ML) techniques have recently enabled enormous gains in sensitivity to new phenomena across the sciences. In particle physics, much of this progress has relied on excellent simulations of a wide range of physical processes. However, due to the sophistication of modern machine learning algorithms and their reliance on high-quality training samples, discrepancies between simulation and experimental data can significantly limit their effectiveness. In this work, we present a solution to this ``misspecification'' problem: a model calibration approach based on optimal transport, which we apply to high-dimensional simulations for the first time. We demonstrate the performance of our approach through jet tagging, using a dataset inspired by the CMS experiment at the Large Hadron Collider. A 128-dimensional internal jet representation from a powerful general-purpose classifier is studied; after calibrating this internal ``latent'' representation, we find that a wide variety of quantities derived from it for downstream tasks are also properly calibrated: using this calibrated high-dimensional representation, powerful new applications of jet flavor information can be utilized in LHC analyses. This is a key step toward allowing the unbiased use of ``foundation models'' in particle physics. More broadly, this calibration framework has broad applications for correcting high-dimensional simulations across the sciences.
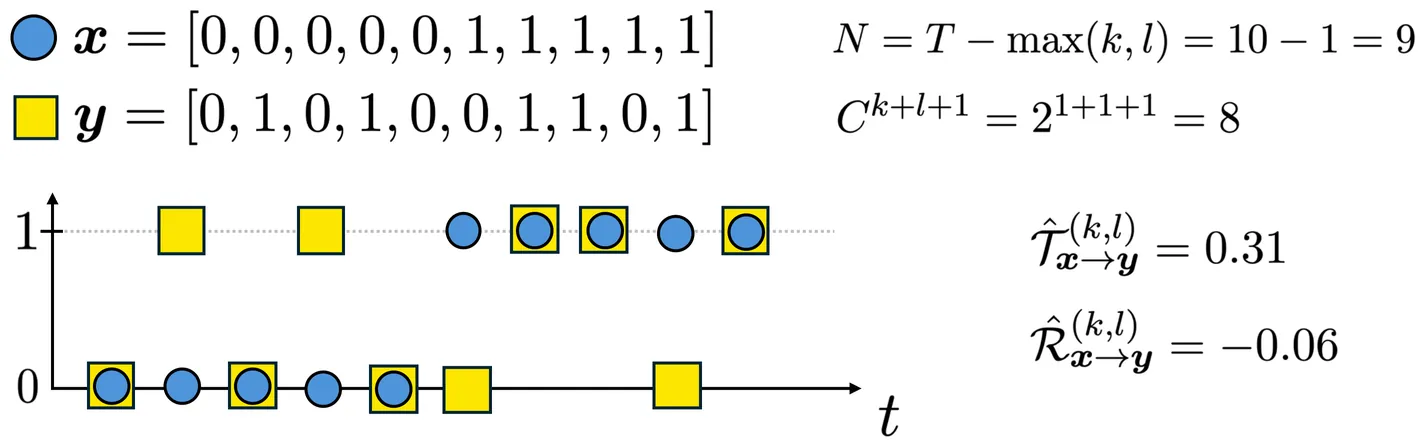
Transfer entropy is a widely used measure for quantifying directed information flows in complex systems. While the challenges of estimating transfer entropy for continuous data are well known, it has two major shortcomings for data of finite cardinality: it exhibits a substantial positive bias for sparse bin counts, and it has no clear means to assess statistical significance. By computing information content in finite data streams without explicitly considering symbols as instances of random variables, we derive a transfer entropy measure which is asymptotically equivalent to the standard plug-in estimator but remedies these issues for time series of small size and/or high cardinality, permitting a fully nonparametric assessment of statistical significance without simulation.
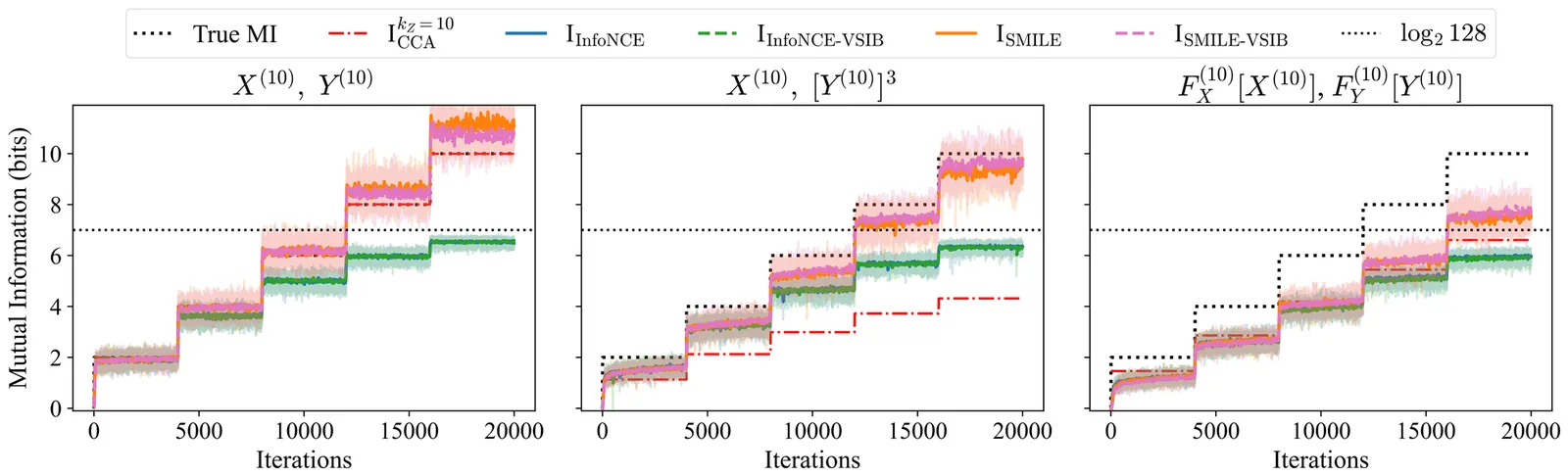
Mutual information (MI) is a fundamental measure of statistical dependence between two variables, yet accurate estimation from finite data remains notoriously difficult. No estimator is universally reliable, and common approaches fail in the high-dimensional, undersampled regimes typical of modern experiments. Recent machine learning-based estimators show promise, but their accuracy depends sensitively on dataset size, structure, and hyperparameters, with no accepted tests to detect failures. We close these gaps through a systematic evaluation of classical and neural MI estimators across standard benchmarks and new synthetic datasets tailored to challenging high-dimensional, undersampled regimes. We contribute: (i) a practical protocol for reliable MI estimation with explicit checks for statistical consistency; (ii) confidence intervals (error bars around estimates) that existing neural MI estimator do not provide; and (iii) a new class of probabilistic critics designed for high-dimensional, high-information settings. We demonstrate the effectiveness of our protocol with computational experiments, showing that it consistently matches or surpasses existing methods while uniquely quantifying its own reliability. We show that reliable MI estimation is sometimes achievable even in severely undersampled, high-dimensional datasets, provided they admit accurate low-dimensional representations. This broadens the scope of applicability of neural MI estimators and clarifies when such estimators can be trusted.
Brightness is a critical metric for optimizing the design of neutron sources and beamlines, yet there is no direct way to calculate brightness within most Monte Carlo packages used for neutron source simulation. In this paper, we present Brightify, an open-source Python-based tool designed to calculate brightness from Monte Carlo Particle List (MCPL) files, which can be extracted from several Monte Carlo simulation packages. Brightify provides an efficient computational approach to calculate brightness for any particle type and energy spectrum recorded in the MCPL file. It enables localized, directionally-resolved brightness evaluations by scanning across both spatial and angular domains, facilitating the identification of positions and directions corresponding to maximum brightness. This functionality is particularly valuable for identifying brightness hotspots and helping fine-tune the design of neutron sources for optimal performance. We validate Brightify against standard methods, such as surface current tally and point estimator tally, and demonstrate its accuracy and adaptability, particularly in high-resolution analyses. By overcoming the limitations of traditional methods, Brightify streamlines neutron source re-optimization, reduces computational burden, and accelerates source development workflows. The full code is available on the Brightify GitHub repository.
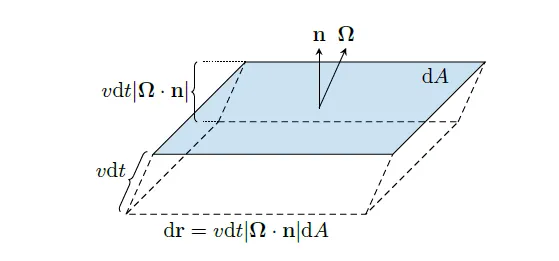
Two maximum likelihood-based algorithms for unfolding or deconvolution are considered: the Richardson-Lucy method and the Data Unfolding method with Mean Integrated Square Error (MISE) optimization [10]. Unfolding is viewed as a procedure for estimating an unknown probability density function. Both external and internal quality assessment methods can be applied for this purpose. In some cases, external criteria exist to evaluate deconvolution quality. A typical example is the deconvolution of a blurred image, where the sharpness of the restored image serves as an indicator of quality. However, defining such external criteria can be challenging, particularly when a measurement has not been performed previously. In such instances, internal criteria are necessary to assess the quality of the result independently of external information. The article discusses two internal criteria: MISE for the unfolded distribution and the condition number of the correlation matrix of the unfolded distribution. These internal quality criteria are applied to a comparative analysis of the two methods using identical numerical data. The results of the analysis demonstrate the superiority of the Data Unfolding method with MISE optimization over the Richardson-Lucy method.
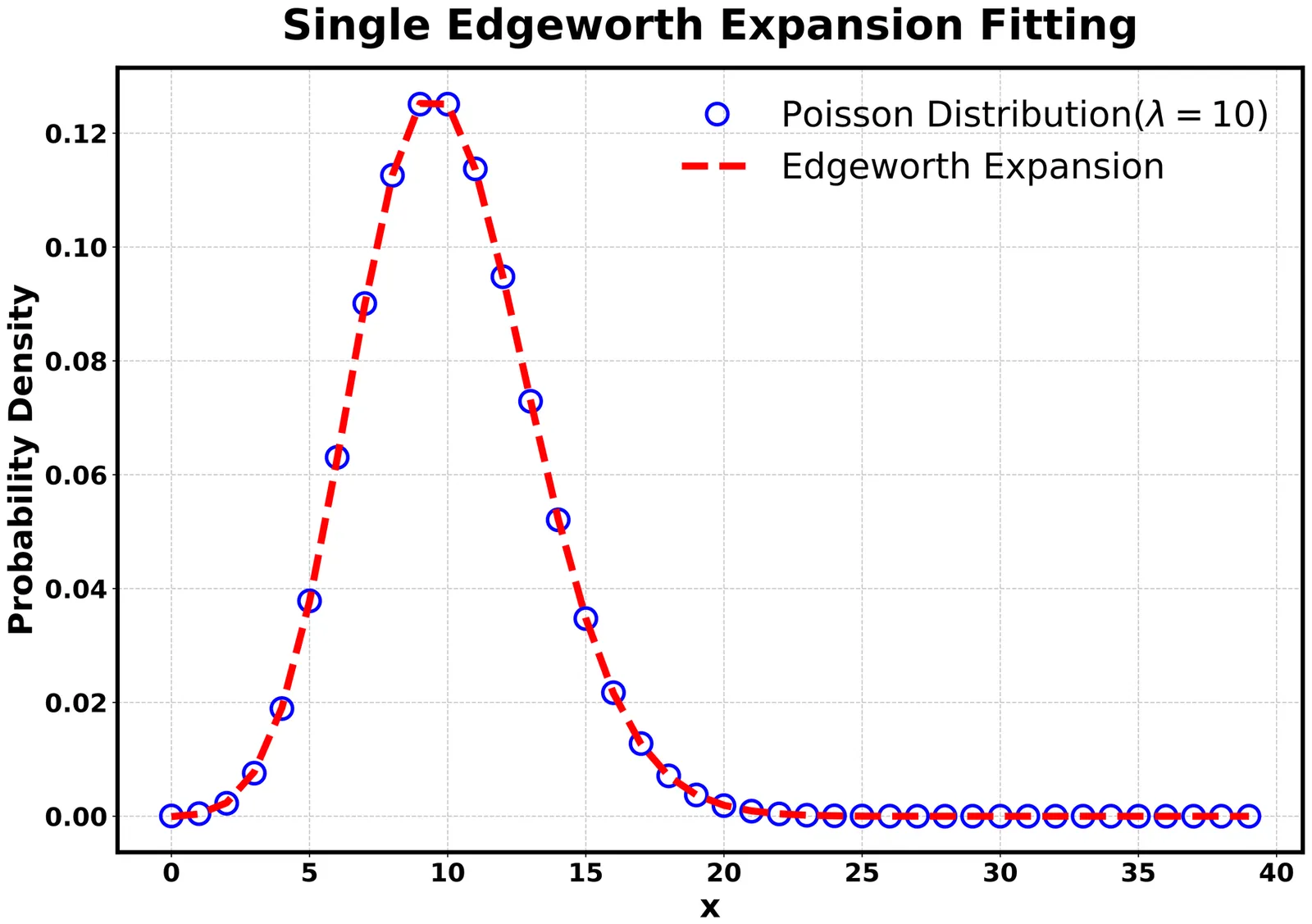
We propose a novel centrality definition-independent method for analyzing higher-order cumulants, specifically addressing the challenge of volume fluctuations that dominate in low-energy heavy-ion collisions. This method reconstructs particle number distributions using the Edgeworth expansion, with parameters optimized via a combination of differential evolution algorithm and Bayesian inference. Its effectiveness is validated using UrQMD model simulations and benchmarked against traditional approaches, including centrality definitions based on particle multiplicity. Our results show that the proposed framework yields cumulant patterns consistent with those obtained using number of participant nucleon ($N_{\text{part}}$) based centrality observables, while eliminating the conventional reliance on centrality determination. This consistency confirms the method's ability to extract genuine physical signals, thereby paving the way for probing the intrinsic thermodynamic properties of the produced medium through event-by-event fluctuations.