Atomic and Molecular Clusters
arXiv:physics.atm-clus
Atomic and molecular clusters, nanoparticles, and their spectroscopy.
2 papers
Coordination-driven magic numbers in protonated argon clusters
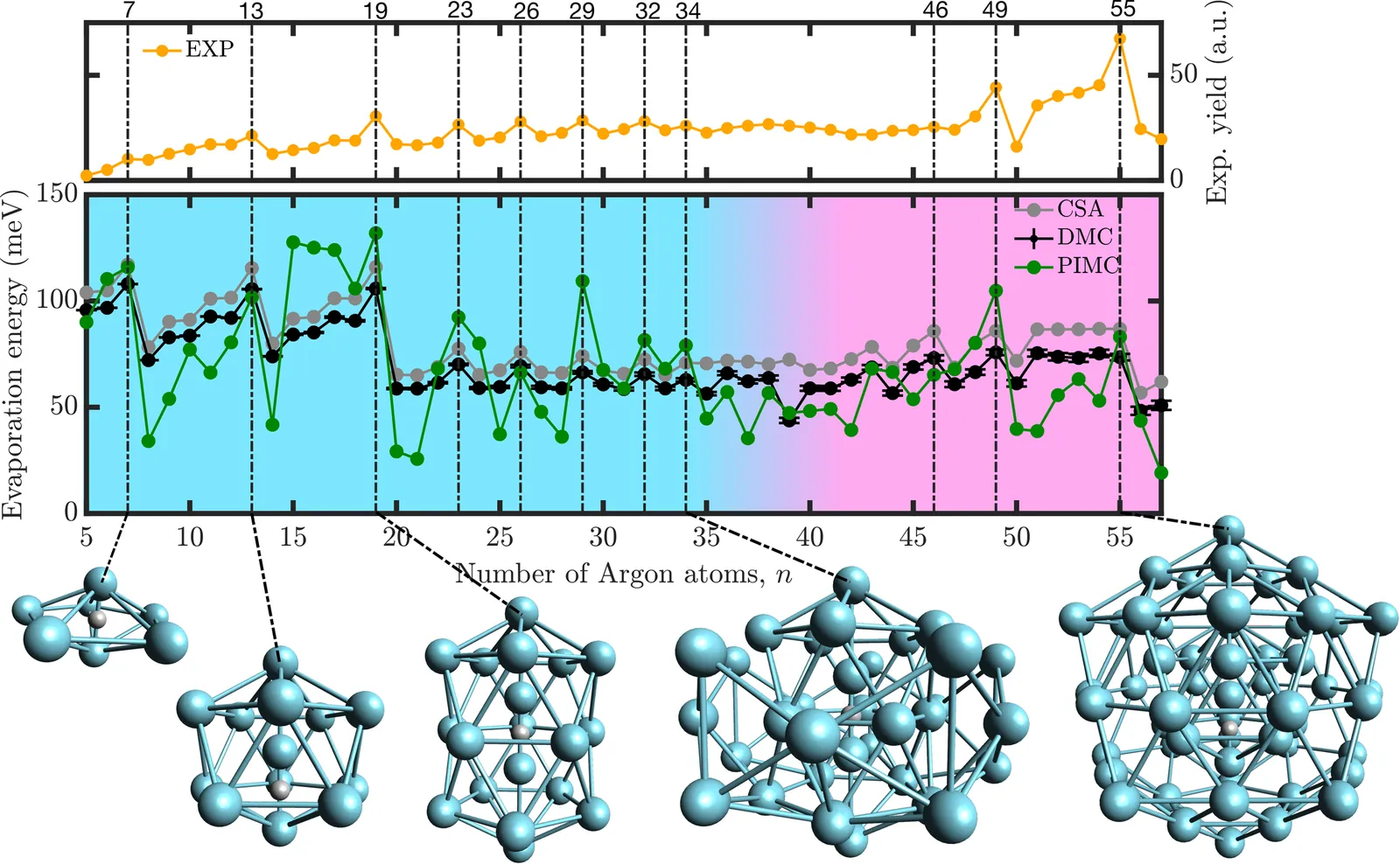
The structural properties of rare-gas clusters can be primarily described by a simple sphere packing model or by pairwise interactions. Remarkably, adding a single proton yields a large set of magic numbers that has remained unexplained. In this Letter, we unravel their origin by combining quantum Monte Carlo techniques with many-body ab initio potentials that correctly capture the proton's coordination environment. Thanks to this approach, we find that argon atoms are mainly localized around the classical minimum, resulting in a particularly rigid behavior in stark contrast to lighter rare-gas clusters. Moreover, as cluster size increases, we identify a clear structural transition from many-body coordination-driven stability to a regime dominated by two-body interactions, reflecting a reshaping of the underlying potential energy landscape.
2601.00591Jan 2026
View
A note on the minimal pairwise distance in optimal Lennard-Jones $N$-body clusters
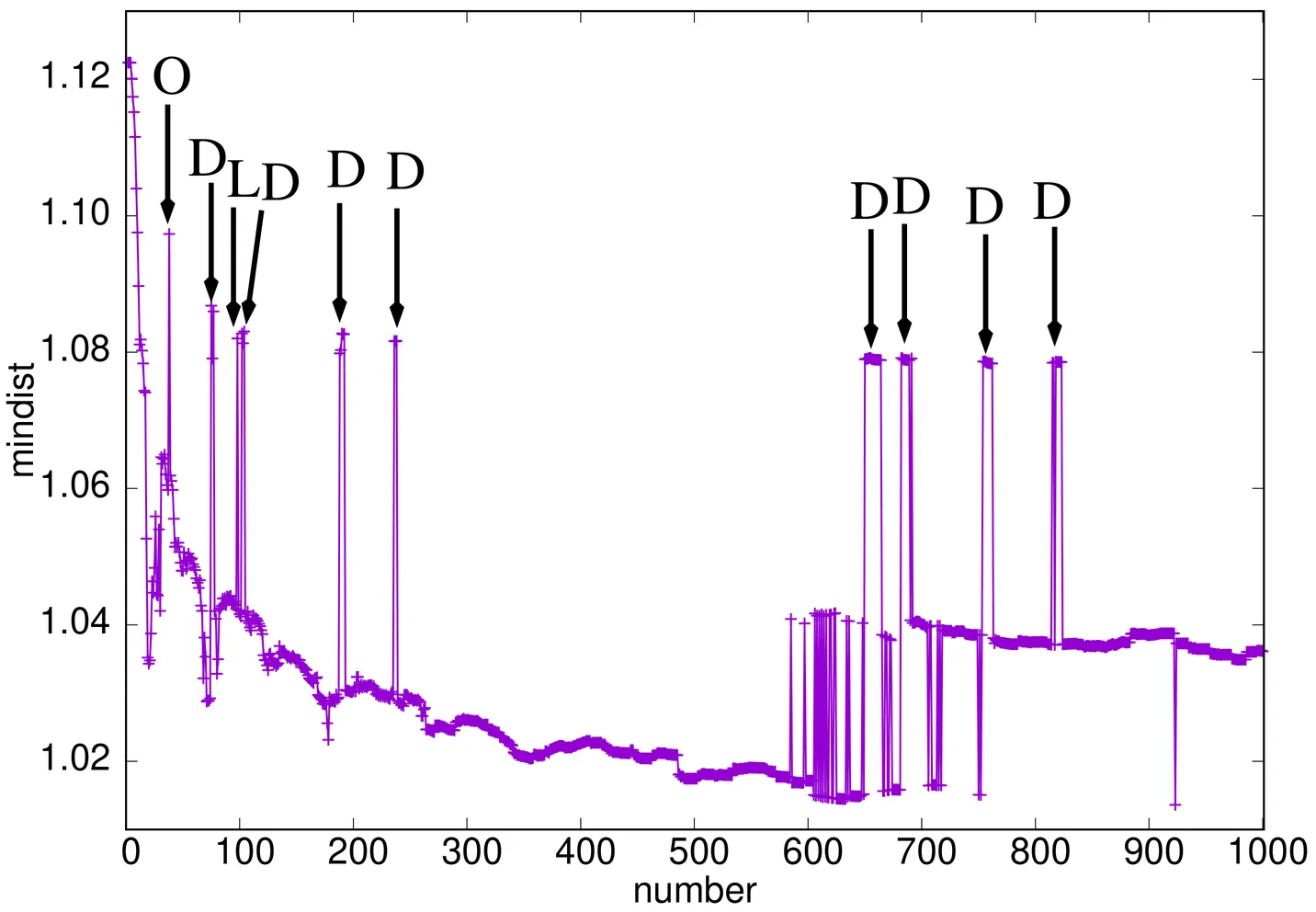
Good a-priori bounds on the smallest pairwise distance $r_{\rm{min}}(\mbox{LJ}_N^{\rm{gmin}})$ for a three-dimensional (3D) Lennard-Jones $N$-body cluster of globally minimal energy can significantly reduce the computational search space in the NP-hard problem to find this configuration. In this contribution the virial theorem is exploited for this purpose. We prove that if a configuration ${C}^{(N)}$ is a member of $\mbox{LJ}_N^{\rm{equ}}$ (the stationary points), then $r_{\rm{min}}({C}^{(N)}) \leq r_{\rm{min}}(\mbox{LJ}_2^{\rm{gmin}})$. It is also shown that if ${C}^{(N)}\in$ LJ$_N^{\rm{gmin}}\subset$ LJ$_N^{\rm{equ}}$, equality holds if and only if $N\in\{2,3,4\}$. We conjecture that $r_{\rm{min}}(\mbox{LJ}_N^{\rm{gmin}}) >1$ in units for which $r_{\rm{min}}(\mbox{LJ}_2^{\rm{gmin}})= 2^\frac16 \approx 1.122462048$. This conjectured lower bound, if correct, would improve the best lower bound currently known, $r_{\rm{min}}(\mbox{LJ}_N^{\rm{gmin}})\geq 0.767764$, by about 25$\%$. In these units the smallest minimal pair distance found through numerical searches for LJ$_N^{\rm{gmin}}$ with $N\leq 1000$ is $r_{\rm{min}}(\mbox{LJ}_{923}^{\rm{gmin}}) \approx 1.01361$, so the conjectured lower bound would presumably be close to optimal. From the virial theorem we obtain an identity for any ${C}^{(N)}\in \mbox{LJ}_N^{\rm{equ}}$, which expresses $r_{\rm{min}}({C}^{(N)})$ in terms of the distribution of relative distances in ${C}^{(N)}$. This result reveals interesting connections with the Erdős distance, and related problems.
2511.15008Nov 2025
View