Computational Physics
Computational methods, numerical algorithms for physics problems.
Computational methods, numerical algorithms for physics problems.
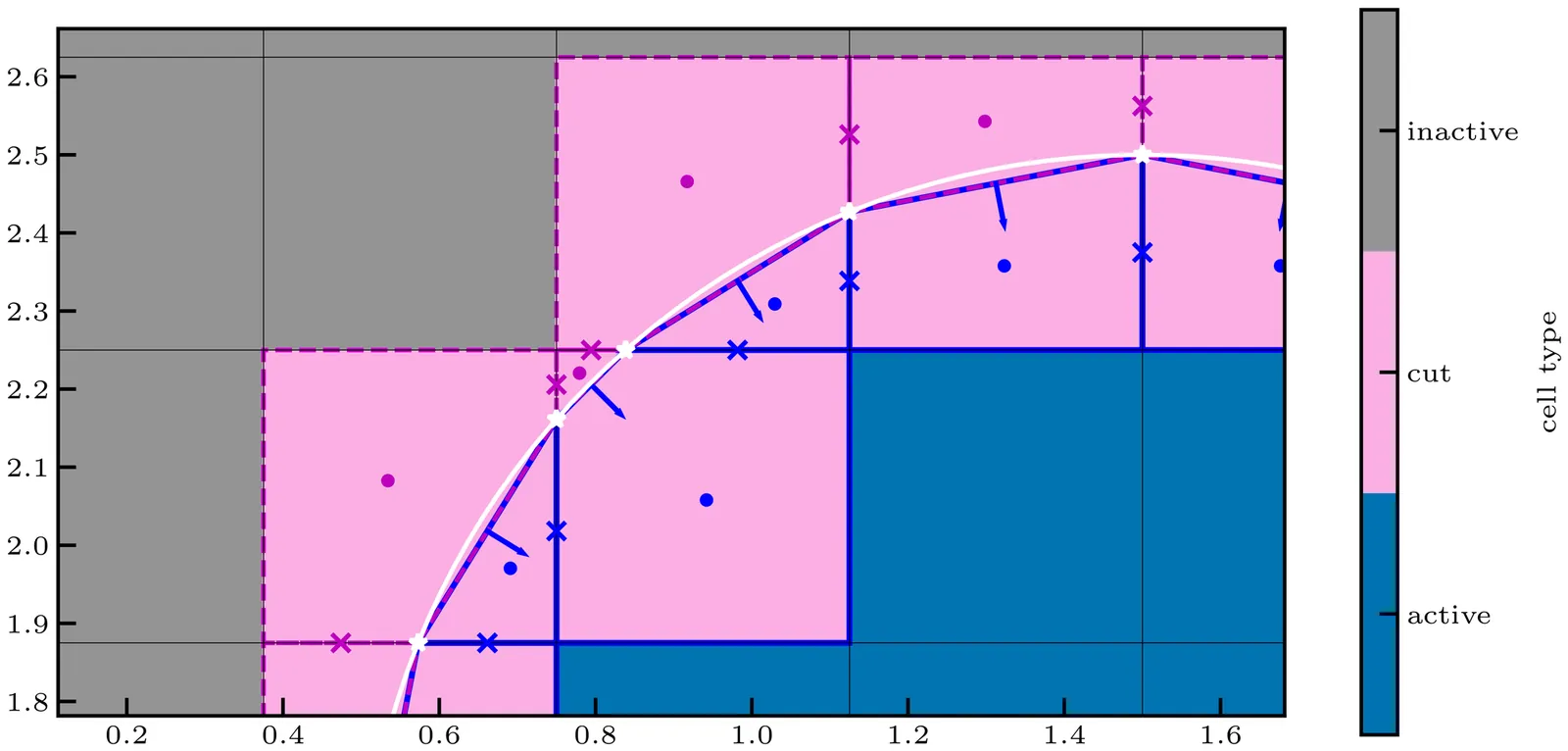
Motivated by the increased interest in pulsed-power magneto-inertial fusion devices in recent years, we present a method for implementing an arbitrarily shaped embedded boundary on a Cartesian mesh while solving the equations of compressible resistive magnetohydrodynamics. The method is built around a finite volume formulation of the equations in which a Riemann solver is used to compute fluxes on the faces between grid cells, and a face-centered constrained transport formulation of the induction equation. The small time step problem associated with the cut cells is avoided by always computing fluxes on the faces and edges of the Cartesian mesh. We extend the method to model a moving interface between two materials with different properties using a ghost-fluid approach, and show some preliminary results including shock-wave-driven and magnetically-driven dynamical compressions of magnetohydrostatic equilibria. We present a thorough verification of the method and show that it converges at second order in the absence of discontinuities, and at first order with a discontinuity in material properties.
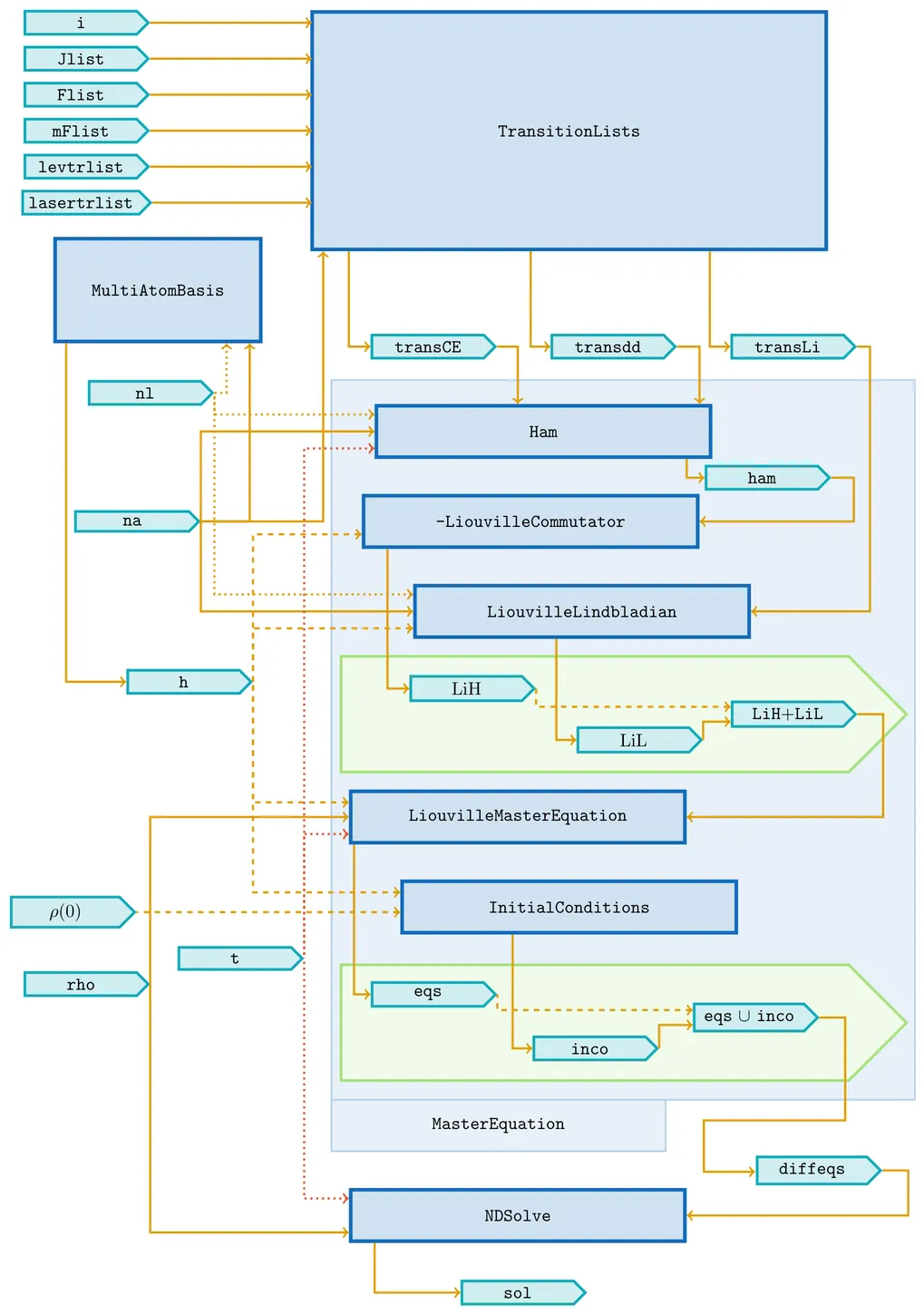
MulAtoLEG (Multi-Atom Liouville Equation Generator) is an open-source Mathematica package for generating Liouville superoperators and Liouville equations, specialized for multilevel atomic systems comprising an arbitrary number of atoms. This scheme is based on an extension to multilevel atomic systems, originally developed by Lehmberg [R. H. Lehmberg, Phys. Rev. A 2, 883 (1970)] as an adjoint master equation for ensembles of two-level emitters and later reformulated by Genes [M. Reitz, C. Sommer and C. Genes, PRX Quantum 3, 010201 (2022)] as a master equation. The package facilitates the generation of equations for complex transition configurations in alkali atoms. Although primarily designed for atomic systems, it can also generate the master and adjoint master equations for general Hamiltonians and Lindbladians. In addition, it includes functionalities to construct the differential equations in the dressed-state basis, where, in many cases, the non-unitary evolution operator can be determined explicitly. To maximize computational efficiency, the package leverages Mathematica's vectorization and sparse linear algebra capabilities. Since MulAtoLEG produces exact equations without approximations, the feasible system size is naturally limited by the available computational resources.
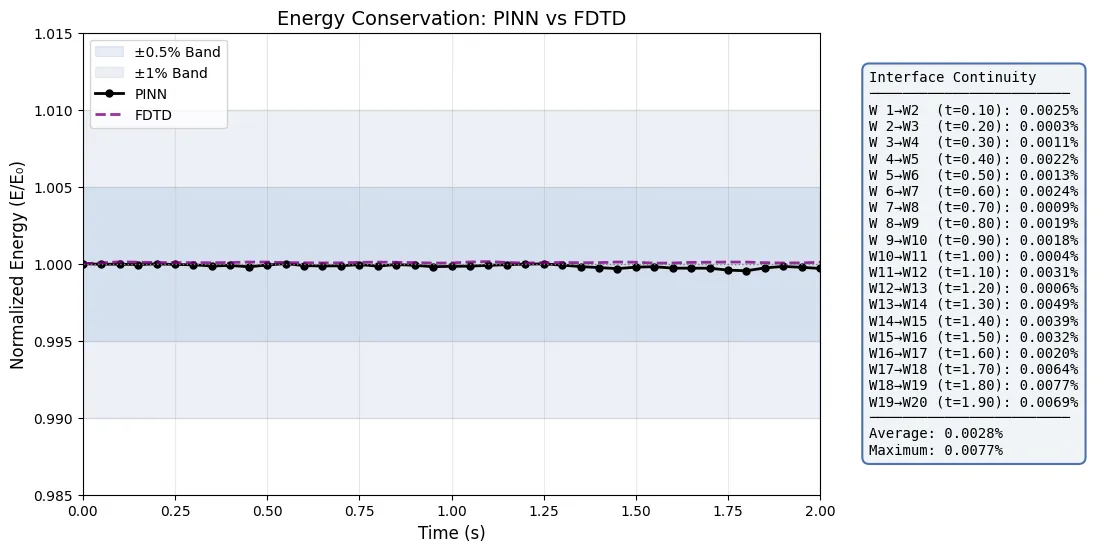
Physics-Informed Neural Networks (PINNs) are a methodology that aims to solve physical systems by directly embedding PDE constraints into the neural network training process. In electromagnetism, where well-established methodologies such as FDTD and FEM already exist, new methodologies are expected to provide clear advantages to be accepted. Despite their mesh-free nature and applicability to inverse problems, PINNs can exhibit deficiencies in terms of accuracy and energy metrics when compared to FDTD solutions. This study demonstrates hybrid training strategies can bring PINNs closer to FDTD-level accuracy and energy consistency. This study presents a hybrid methodology addressing common challenges in wave propagation scenarios. The causality collapse problem in time-dependent PINN training is addressed via time marching and causality-aware weighting. In order to mitigate the discontinuities that are introduced by time marching, a two-stage interface continuity loss is applied. In order to suppress loss accumulation, which is manifested as cumulative energy drift in electromagnetic waves, a local Poynting-based regularizer has been developed. In the developed PINN model, high field accuracy is achieved with an average 0.09\% $NRMSE$ and 1.01\% $L^2$ error over time. Energy conservation is achieved on the PINN side with only a 0.024\% relative energy mismatch in the 2D PEC cavity scenario. Training is performed without labeled field data, using only physics-based residual losses; FDTD is used solely for post-training evaluation. The results demonstrate that PINNs can achieve competitive results with FDTD in canonical electromagnetic examples and are a viable alternative.

Continuous fiber-reinforced composite manufactured by additive manufacturing (CFRC-AM) offers opportunities for printing lightweight materials with high specific strength. However, their performance is sensitive to the interaction of process and material parameters, making exhaustive experimental testing impractical. In this study, we introduce a data-efficient, multi-input, multi-target learning approach that integrates Latin Hypercube Sampling (LHS)-guided experimentation with a squeeze-and-excitation wide and deep neural network (SE-WDNN) to jointly predict multiple mechanical and manufacturing properties of CFRC-AMs based on different manufacturing parameters. We printed and tested 155 specimens selected from a design space of 4,320 combinations using a Markforged Mark Two 3D printer. The processed data formed the input-output set for our proposed model. We compared the results with those from commonly used machine learning models, including feedforward neural networks, Kolmogorov-Arnold networks, XGBoost, CatBoost, and random forests. Our model achieved the lowest overall test error (MAPE = 12.33%) and showed statistically significant improvements over the baseline wide and deep neural network for several target variables (paired t-tests, p <= 0.05). SHapley Additive exPlanations (SHAP) analysis revealed that reinforcement strategy was the major influence on mechanical performance. Overall, this study demonstrates that the integration of LHS and SE-WDNN enables interpretable and sample-efficient multi-target predictions, guiding parameter selection in CFRC-AM with a balance between mechanical behavior and manufacturing metrics.
Modern heterogeneous high-performance computing (HPC) systems powered by advanced graphics processing unit (GPU) architectures enable accelerating computing with unprecedented performance and scalability. Here, we present a GPU-accelerated solver for the three-dimensional (3D) time-dependent Dirac equation optimized for distributed HPC systems. The solver named GaDE is designed to simulate the electron dynamics in atoms induced by electromagnetic fields in the relativistic regime. It combines MPI with CUDA/HIP to target both NVIDIA and AMD GPU architectures. We discuss our implementation strategies in which most of the computations are carried out on GPUs, taking advantage of the GPU-aware MPI feature to optimize communication performance. We evaluate GaDE on the pre-exascale supercomputer LUMI, powered by AMD MI250X GPUs and HPE's Slingshot interconnect. Single-GPU performance on NVIDIA A100, GH200, and AMD MI250X shows comparable performance between A100 and MI250X in compute and memory bandwidth, with GH200 delivering higher performance. Weak scaling on LUMI demonstrates exceptional scalability, achieving 85% parallel efficiency across 2048 GPUs, while strong scaling delivers a 16x speedup on 32 GPUs - 50% efficiency for a communication-intensive, time-dependent Dirac equation solver. These results demonstrate GaDE's high scalability, making it suitable for exascale systems and enabling predictive simulations for ultra-intense laser experiments probing relativistic quantum effects.
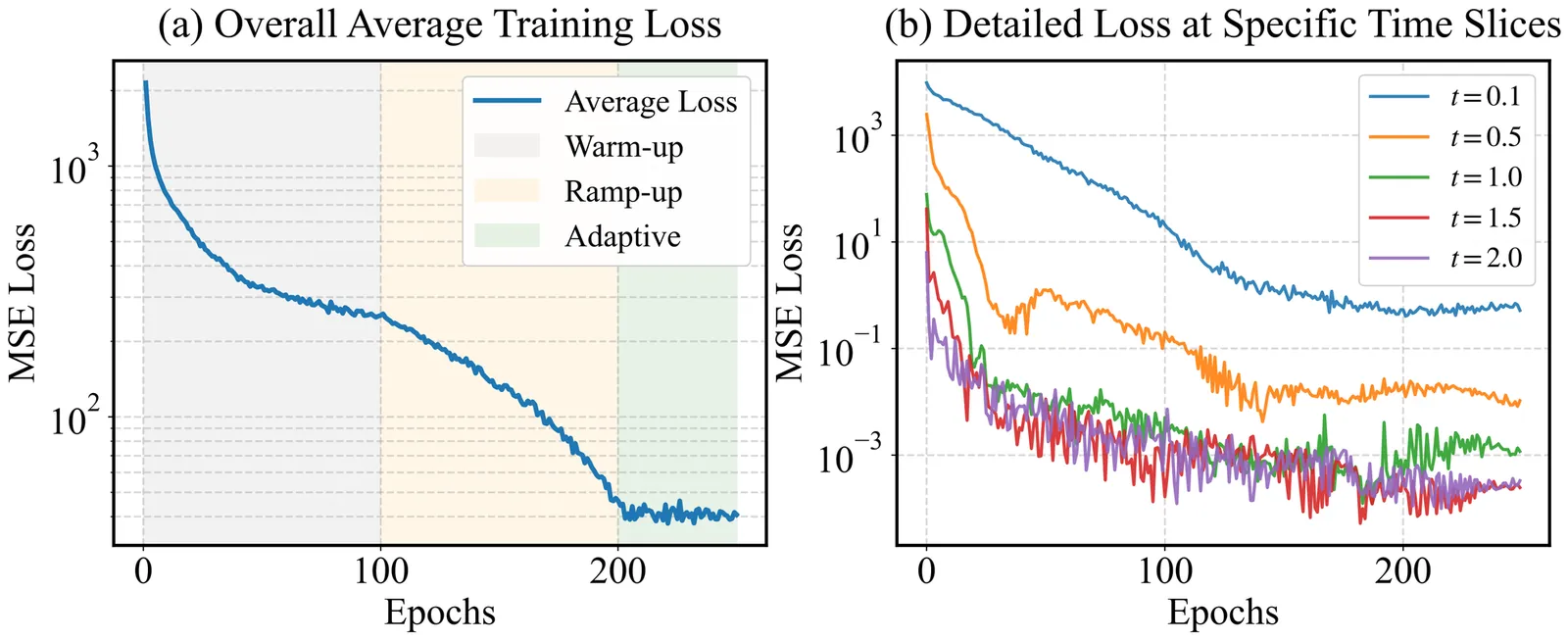
Solving high-dimensional Fokker-Planck (FP) equations is a challenge in computational physics and stochastic dynamics, due to the curse of dimensionality (CoD) and the bottleneck of evaluating second-order diffusion terms. Existing deep learning approaches, such as Physics-Informed Neural Networks (PINNs), face computational challenges as dimensionality increases, driven by the $O(D^2)$ complexity of automatic differentiation for second-order derivatives. While recent probability flow approaches bypass this by learning score functions or matching velocity fields, they often involve serial computational operations or depend on sampling efficiency in complex distributions. To address these issues, we propose the Self-Consistent Probability Flow (SCPF) method. We reformulate the second-order FP equation into an equivalent first-order deterministic Probability Flow ODE (PF-ODE) constraint. Unlike score matching or velocity matching, SCPF solves this problem by minimizing the residual of the PF-ODE continuity equation, which avoids explicit Hessian computation. We leverage Continuous Normalizing Flows (CNF) combined with the Hutchinson Trace Estimator (HTE) to reduce the training complexity to linear scale $O(D)$, achieving an effective $O(1)$ wall-clock time on GPUs. To address data sparsity in high dimensions, we apply a generative adaptive sampling strategy and theoretically prove that dynamically aligning collocation points with the evolving probability mass is a necessary condition to bound the approximation error. Experiments on diverse benchmarks -- ranging from anisotropic Ornstein-Uhlenbeck (OU) processes and high-dimensional Brownian motions with time-varying diffusion terms, to Geometric OU processes featuring non-Gaussian solutions -- demonstrate that SCPF effectively mitigates the CoD, maintaining high accuracy and constant computational cost for problems up to 100 dimensions.
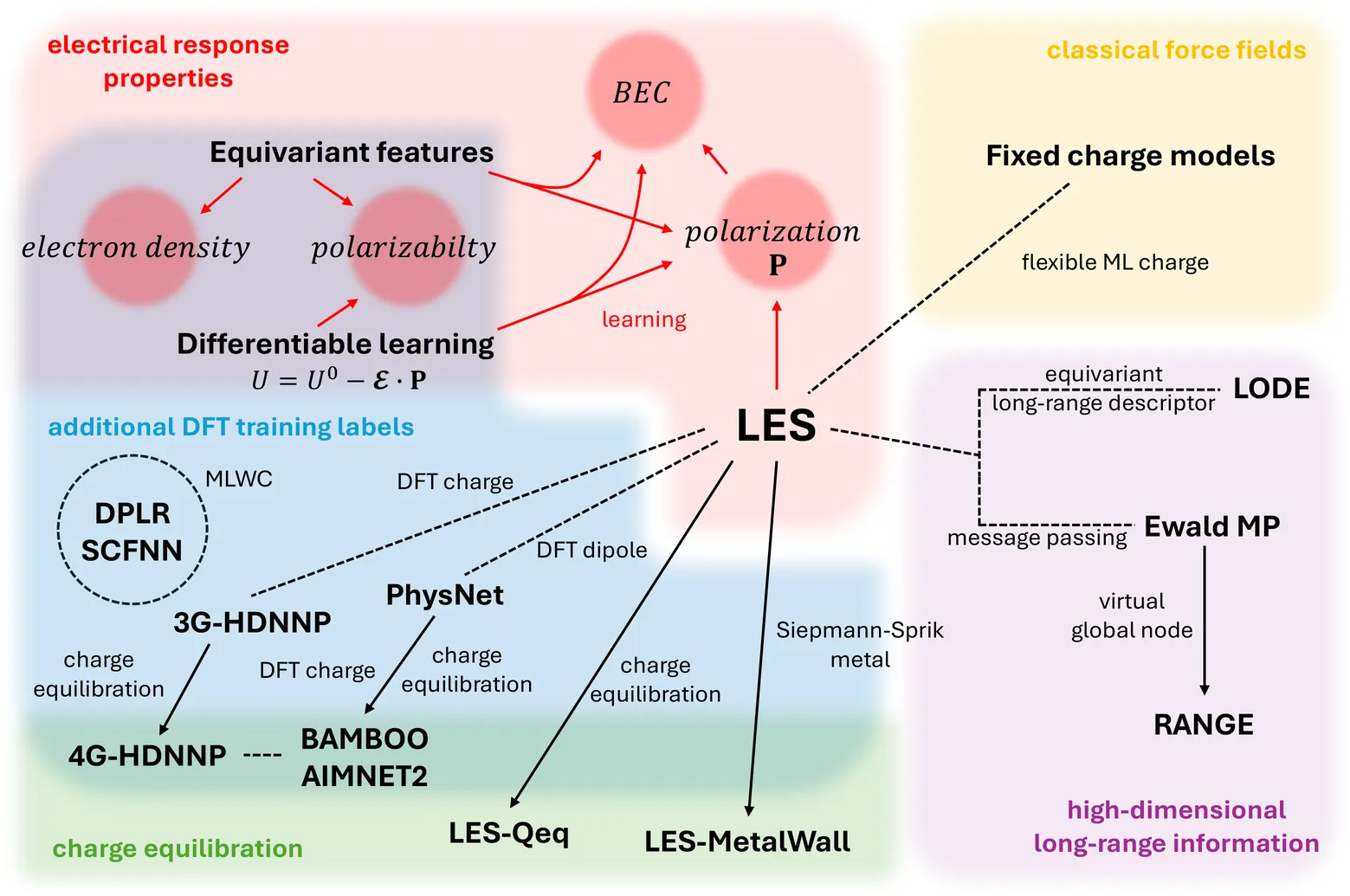
The lack of long-range electrostatics is a key limitation of modern machine learning interatomic potentials (MLIPs), hindering reliable applications to interfaces, charge-transfer reactions, polar and ionic materials, and biomolecules. In this Perspective, we distill two design principles behind the Latent Ewald Summation (LES) framework, which can capture long-range interactions, charges, and electrical response just by learning from standard energy and force training data: (i) use a Coulomb functional form with environment-dependent charges to capture electrostatic interactions, and (ii) avoid explicit training on ambiguous density functional theory (DFT) partial charges. When both principles are satisfied, substantial flexibility remains: essentially any short-range MLIP can be augmented; charge equilibration schemes can be added when desired; dipoles and Born effective charges can be inferred or finetuned; and charge/spin-state embeddings or tensorial targets can be further incorporated. We also discuss current limitations and open challenges. Together, these minimal, physics-guided design rules suggest that incorporating long-range electrostatics into MLIPs is simpler and perhaps more broadly applicable than is commonly assumed.
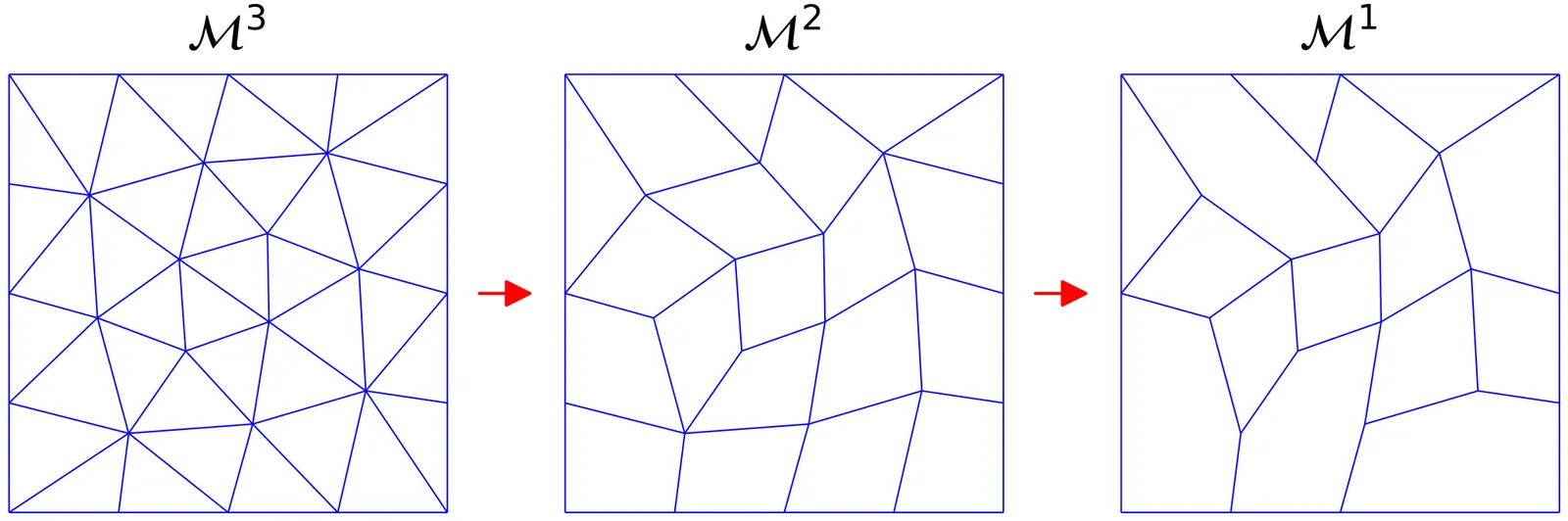
We develop a sparse multiscale operator-adapted wavelet decomposition-based finite element method (FEM) on unstructured polygonal mesh hierarchies obtained via a coarsening procedure. Our approach decouples different resolution levels, allowing each scale to be solved independently and added to the entire solution without the need to recompute coarser levels. At the finest level, the meshes consist of triangular elements which are geometrically coarsened at each step to form convex polygonal elements. Smooth field regions of the domain are solved with fewer, larger, polygonal elements, whereas high-gradient regions are represented by smaller elements, thereby improving memory efficiency through adaptivity. The proposed algorithm computes solutions via sequences of hierarchical sparse linear-algebra operations with nearly linear computational complexity.

Artificial neural networks accurately learn nonlinear, path-dependent material behavior. However, training them typically requires large, diverse datasets, often created via synthetic unit cell simulations. This hinders practical adoption because physical experiments on standardized specimens with simple geometries fail to generate sufficiently diverse stress-strain trajectories. Consequently, an unreasonably large number of experiments or complex multi-axial tests would be needed. This work shows that such networks can be trained from a single specimen subjected to simple uniaxial loading, by designing the specimen using a novel automatically differentiable elastoplastic topology optimization method. Our strategy diversifies the stress-strain states observed in a single test involving plastic deformation. We then employ the automatically differentiable model updating (ADiMU) method to train the neural network surrogates. This work demonstrates that topology-optimized specimens under simple loading can train large neural networks, thereby substantially reducing the experimental burden associated with data-driven material modeling.
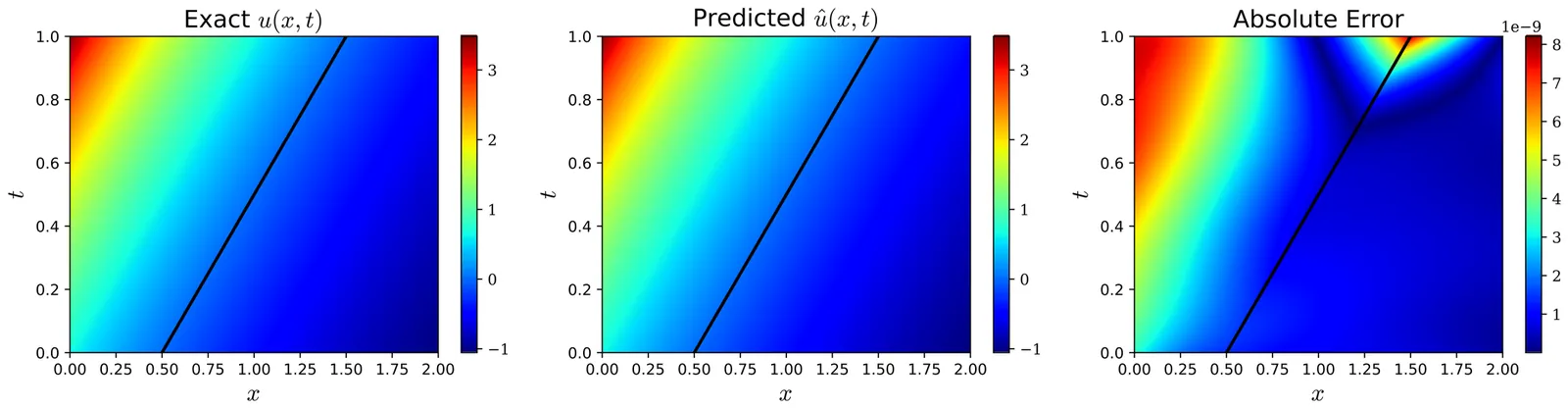
The Stefan problem is a classical free-boundary problem that models phase-change processes and poses computational challenges due to its moving interface and nonlinear temperature-phase coupling. In this work, we develop a physics-informed neural network framework for solving two-phase Stefan problems. The proposed method explicitly tracks the interface motion and enforces the discontinuity in the temperature gradient across the interface while maintaining global consistency of the temperature field. Our approach employs two neural networks: one representing the moving interface and the other for the temperature field. The interface network allows rapid categorization of thermal diffusivity in the spatial domain, which is a crucial step for selecting training points for the temperature network. The temperature network's input is augmented with a modified zero-level set function to accurately capture the jump in its normal derivative across the interface. Numerical experiments on two-phase dynamical Stefan problems demonstrate the superior accuracy and effectiveness of our proposed method compared with the ones obtained by other neural network methodology in literature. The results indicate that the proposed framework offers a robust and flexible alternative to traditional numerical methods for solving phase-change problems governed by moving boundaries. In addition, the proposed method can capture an unstable interface evolution associated with the Mullins-Sekerka instability.
Physics-Informed Neural Networks (PINNs) and more recently Physics-Informed Kolmogorov-Arnold Networks (PIKANs) have emerged as promising approaches for solving partial differential equations (PDEs) without reliance on extensive labeled data. In this work, we propose a novel multi-resolution Hybrid Wavelet-Fourier-Enhanced Physics-Informed Kolmogorov-Arnold Network (HWF-PIKAN) for solving advection problems based on collisionless Boltzmann equation (CBE) with both continuous and discontinuous initial conditions. To validate the effectiveness of the proposed model, we conduct systematic benchmarks on classical advection equations in one and two dimensions. These tests demonstrate the model's ability to accurately capture smooth and abrupt features. We then extend the application of HWF-PIKAN to the high-dimensional phase-space setting by solving the CBE in a continuous-velocity manner. This leverages the Hamiltonian concept of phase-space dynamics to model the statistical behavior of particles in a collisionless system, where advection governs the evolution of a probability distribution function or number density. Comparative analysis against Vanilla PINN, Vanilla PIKAN, as well as Fourier-enhanced and Wavelet-enhanced PIKAN variants, shows that the proposed hybrid model significantly improves solution accuracy and convergence speed. This study highlights the power of multi-resolution spectral feature embeddings in advancing physics-informed deep learning frameworks for complex kinetic equations in both space-time and phase-space.
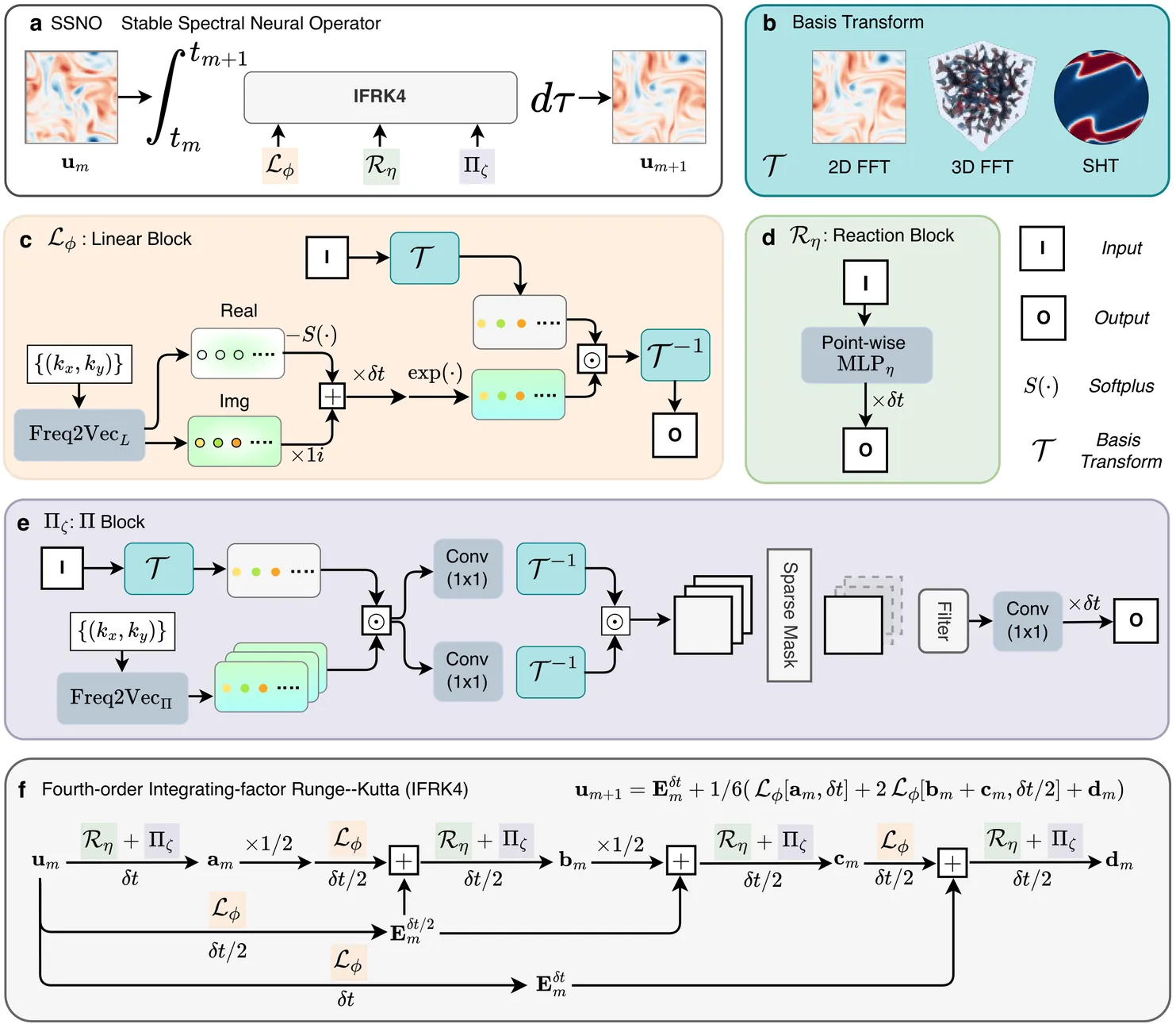
Accurate modeling of spatiotemporal dynamics is crucial to understanding complex phenomena across science and engineering. However, this task faces a fundamental challenge when the governing equations are unknown and observational data are sparse. System stiffness, the coupling of multiple time-scales, further exacerbates this problem and hinders long-term prediction. Existing methods fall short: purely data-driven methods demand massive datasets, whereas physics-aware approaches are constrained by their reliance on known equations and fine-grained time steps. To overcome these limitations, we introduce an equation-free learning framework, namely, the Stable Spectral Neural Operator (SSNO), for modeling stiff partial differential equation (PDE) systems based on limited data. Instead of encoding specific equation terms, SSNO embeds spectrally inspired structures in its architecture, yielding strong inductive biases for learning the underlying physics. It automatically learns local and global spatial interactions in the frequency domain, while handling system stiffness with a robust integrating factor time-stepping scheme. Demonstrated across multiple 2D and 3D benchmarks in Cartesian and spherical geometries, SSNO achieves prediction errors one to two orders of magnitude lower than leading models. Crucially, it shows remarkable data efficiency, requiring only very few (2--5) training trajectories for robust generalization to out-of-distribution conditions. This work offers a robust and generalizable approach to learning stiff spatiotemporal dynamics from limited data without explicit \textit{a priori} knowledge of PDE terms.
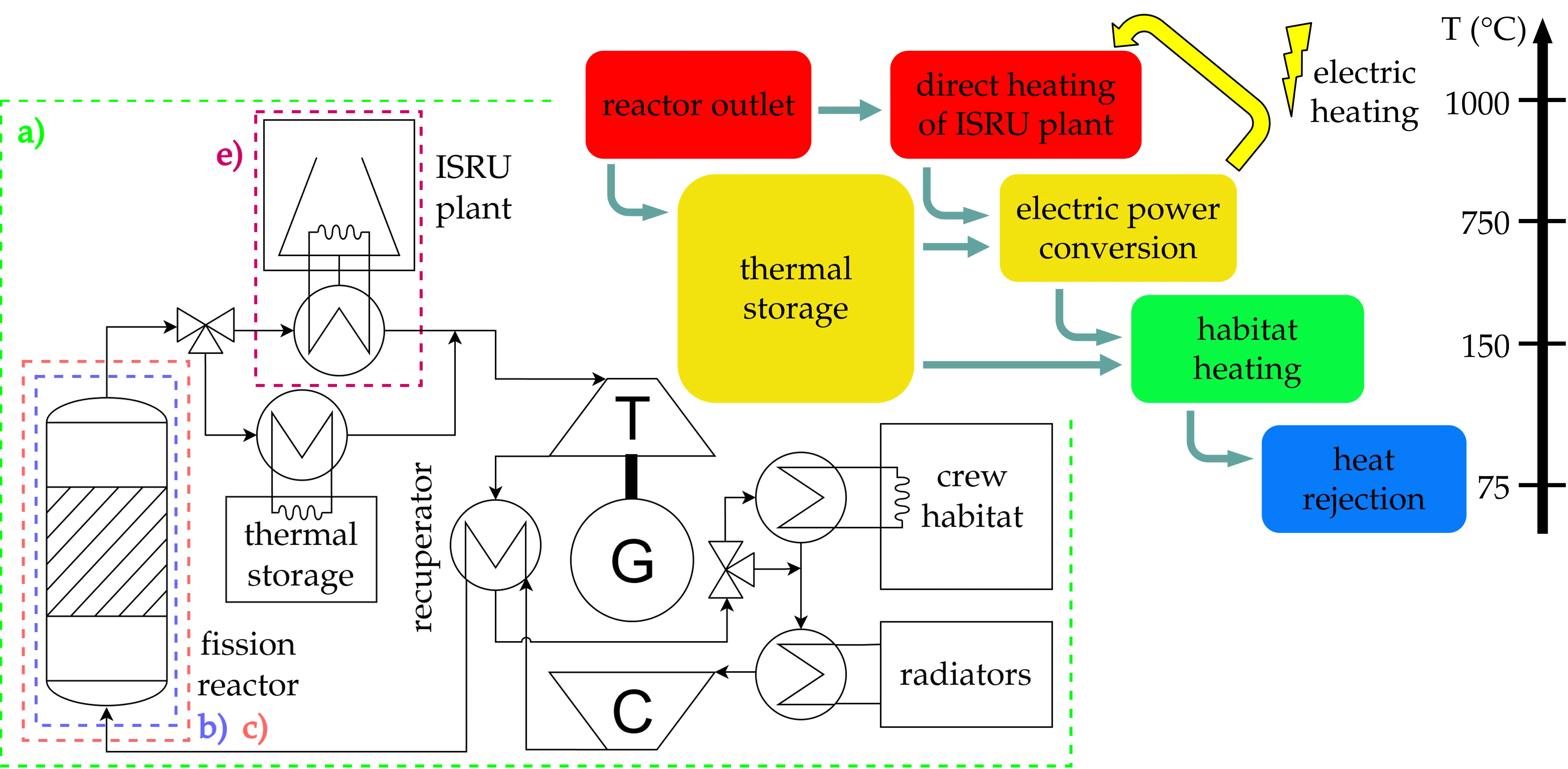
For a sustained human presence on the Moon, robust in-situ resource utilisation supply chains to provide consumables and propellant are necessary. A promising process is molten salt electrolysis, which typically requires temperatures in excess of 900°C. Fission reactors do not depend on solar irradiance and are thus well suited for power generation on the Moon, especially during the 14-day lunar night. As of now, fission reactors have only been considered for electric power generation, but the reactor coolant could also be used directly to heat those processes to their required temperatures. In this work, a concept for a co-generation fission power plant on the Moon that can directly heat a MSE plant to the required temperatures and provide a surplus of electrical energy for the lunar base is presented. The neutron transport code Serpent 2 is used to model a ceramic core, gas-cooled very-high-temperature microreactor design and estimate its lifetime with a burnup simulation in hot conditions with an integrated step-wise criticality search. Calculations show a neutronically feasible operation time of at least 10 years at 100kW thermal power. The obtained power distributions lay a basis for further thermal-hydraulic studies on the technical feasibility of the reactor design and the power plant.
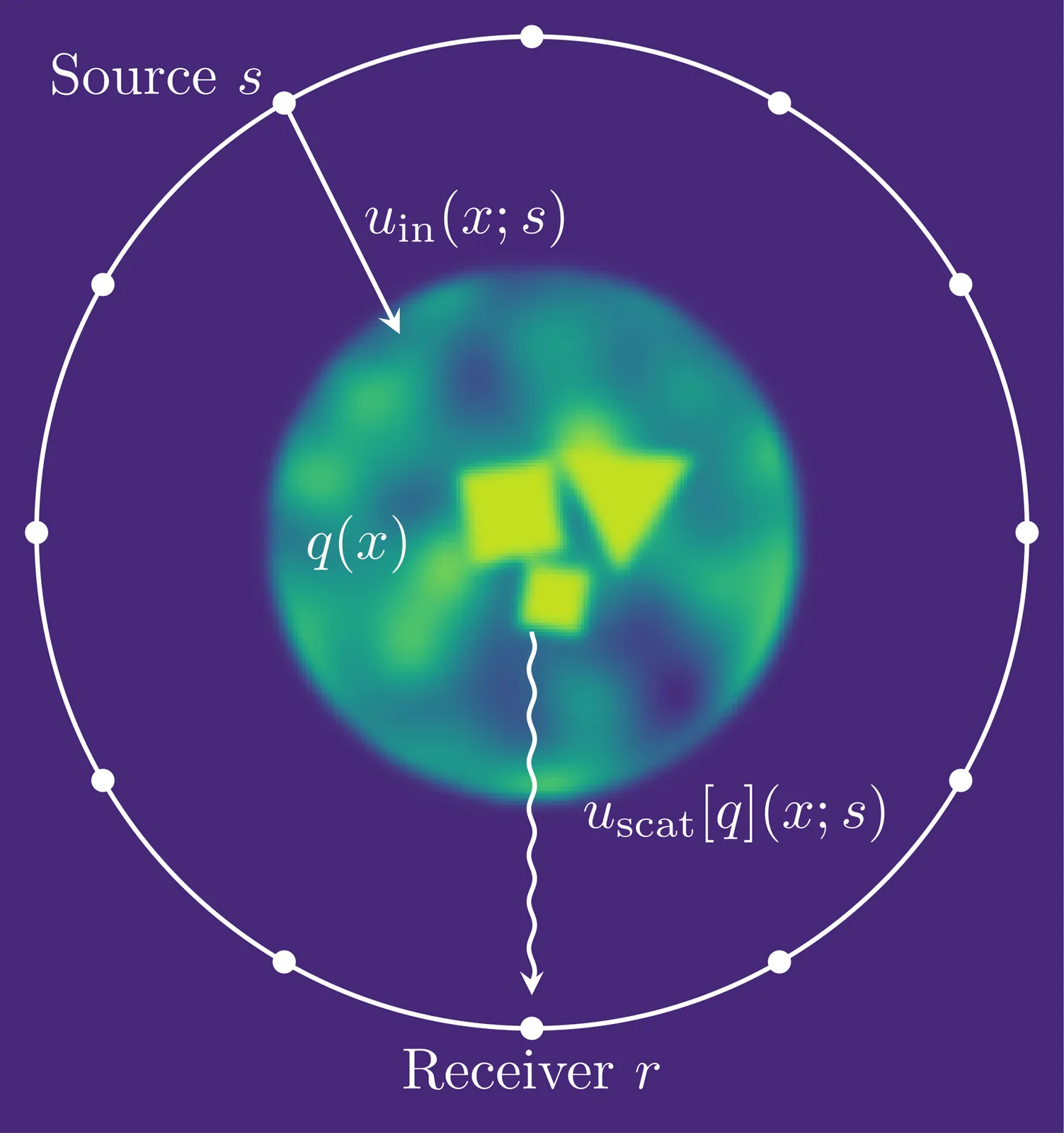
Inverse medium scattering is an ill-posed, nonlinear wave-based imaging problem arising in medical imaging, remote sensing, and non-destructive testing. Machine learning (ML) methods offer increased inference speed and flexibility in capturing prior knowledge of imaging targets relative to classical optimization-based approaches; however, they perform poorly in regimes where the scattering behavior is highly nonlinear. A key limitation is that ML methods struggle to incorporate the physics governing the scattering process, which are typically inferred implicitly from the training data or loosely enforced via architectural design. In this paper, we present a method that endows a machine learning framework with explicit knowledge of problem physics, in the form of a differentiable solver representing the forward model. The proposed method progressively refines reconstructions of the scattering potential using measurements at increasing wave frequencies, following a classical strategy to stabilize recovery. Empirically, we find that our method provides high-quality reconstructions at a fraction of the computational or sampling costs of competing approaches.
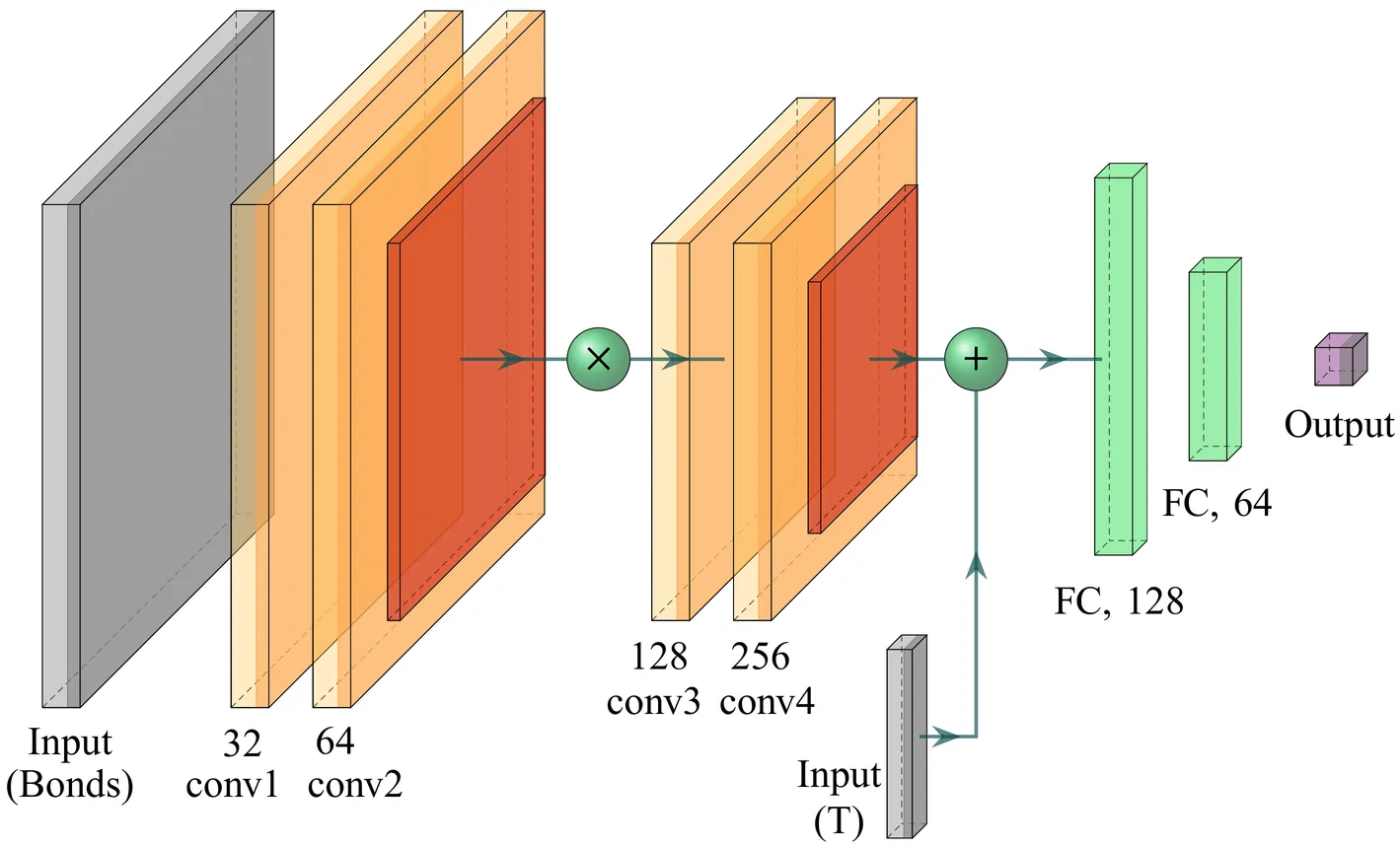
This paper presents a systematic study of the application of convolutional neural networks (CNNs) as an efficient and versatile tool for the analysis of critical and low-temperature phase states in spin system models. The problem of calculating the dependence of the average energy on the spatial distribution of exchange integrals for the Edwards-Anderson model on a square lattice with frustrated interactions is considered. We further construct a single convolutional classifier of phase states of the ferromagnetic Ising model on square, triangular, honeycomb, and kagome lattices, trained on configurations generated by the Swendsen-Wang cluster algorithm. Computed temperature profiles of the averaged posterior probability of the high-temperature phase form clear S-shaped curves that intersect in the vicinity of the theoretical critical temperatures and allow one to determine the critical temperature for the kagome lattice without additional retraining. It is shown that convolutional models substantially reduce the root-mean-square error (RMSE) compared with fully connected architectures and efficiently capture complex correlations between thermodynamic characteristics and the structure of magnetic correlated systems.
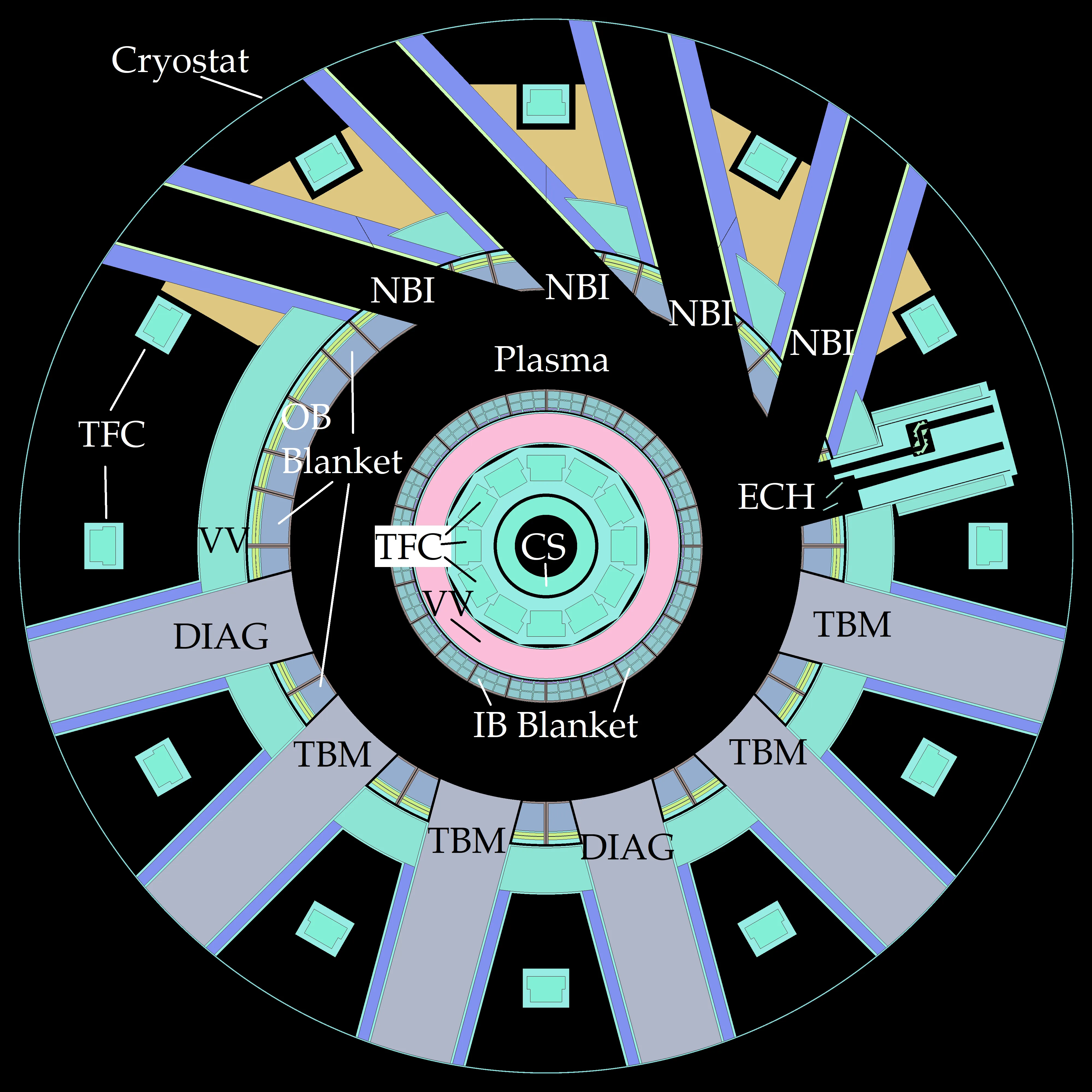
The Volumetric Neutron Source (VNS) tokamak is a proposed fusion reactor for testing and qualification of reactor components for future use in a fusion power facility, and has potential use for radioisotope production. The VNS geometry is modeled in the Serpent and OpenMC neutronics codes. Analog neutron-photon coupled simulations are carried out to compare the model's vacuum vessel and blanket components across codes. In the vacuum vessel, neutron and photon flux maps are calculated, while in the blanket region, neutron and photon spectra, (n,T), and (n,2n) reaction rates are calculated and compared between models. The detector response comparisons found the following: neutron flux and (n,T) reactions achieved excellent agreement, the (n,2n) detector response had good agreement, and photon flux had regional discrepancies depending on Serpent tracking used. Hybrid tracking lead to a relative difference of about 20% in the outboard side blanket, where as employment of delta tracking resulted in less than 1% relative difference. On an HPC cluster, Serpent was found to have shorter computation time than OpenMC in neutron photon coupled simulations using both hybrid tracking and delta tracking, but longer in neutron only simulations. An exemplary radioisotope production case is presented for the demonstration of additional VNS capabilities.
Typical fully conservative discretizations of the Euler compressible single or multi-component fluid equations governed by a real-fluid equation of state exhibit spurious pressure oscillations due to the nonlinearity of the thermodynamic relation between pressure, density, and internal energy. A fully conservative, pressure-equilibrium preserving method and a high-order, fully conservative, approximate pressure-equilibrium preserving method are presented. Both methods are general and can handle an arbitrary equation of state and arbitrary number of species. Unlike existing approaches to discretize the multi-component Euler equations, we do not introduce non conservative updates, overspecified equations, or design for a specific equation of state. The proposed methods are demonstrated on inviscid smooth interface advection problems governed by three equations of state: ideal-gas, stiffened-gas, and van der Waals where we show orders of magnitude reductions in spurious pressure oscillations compared to existing schemes.
Thermal compositional multiphase flow in porous media with phase transitions involves complex nonlinear interactions among flow, transport, and phase equilibrium. This paper presents a persistent-variable formulation for thermal compositional flow using enthalpy to formulate the energy balance and the local equilibrium problem. Equilibrium conditions are derived from a thermodynamically consistent minimization problem using a persistent set of variables, allowing for seamless integration of equilibrium calculations into a fully coupled flow and transport model. This formulation does not require phase stability tests and provides a continuous and full mathematical description of the multiphysics system, suitable for challenging non-isothermal scenarios. To tackle the nonlinearities arising from phase transitions, we embed a local solver for the thermodynamic subproblem within a global Newton solver for the fully implicit system. The local solver exploits the locality of the subproblem for parallelization and leverages the modularity of the persistent-variable formulation for both isothermal and isenthalpic equilibrium conditions locally. We demonstrate the capability of our approach to simulate complex high-enthalpy systems, including narrow-boiling phenomena. The impact of the embedded local solver is analyzed through numerical experiments, demonstrating a reduction in global nonlinear iterations of up to 23 \% with increased use of the local solver. The number of local iterations is controlled with a local solver tolerance and no significant impact on the global iteration number was observed for local residual tolerances as high as $1e-3$. The persistent-variable approach using enthalpy and the modularity of the embedded local solver advance the usage of equilibrium calculations in multiphase flow simulations and are suitable for high-enthalpy applications.
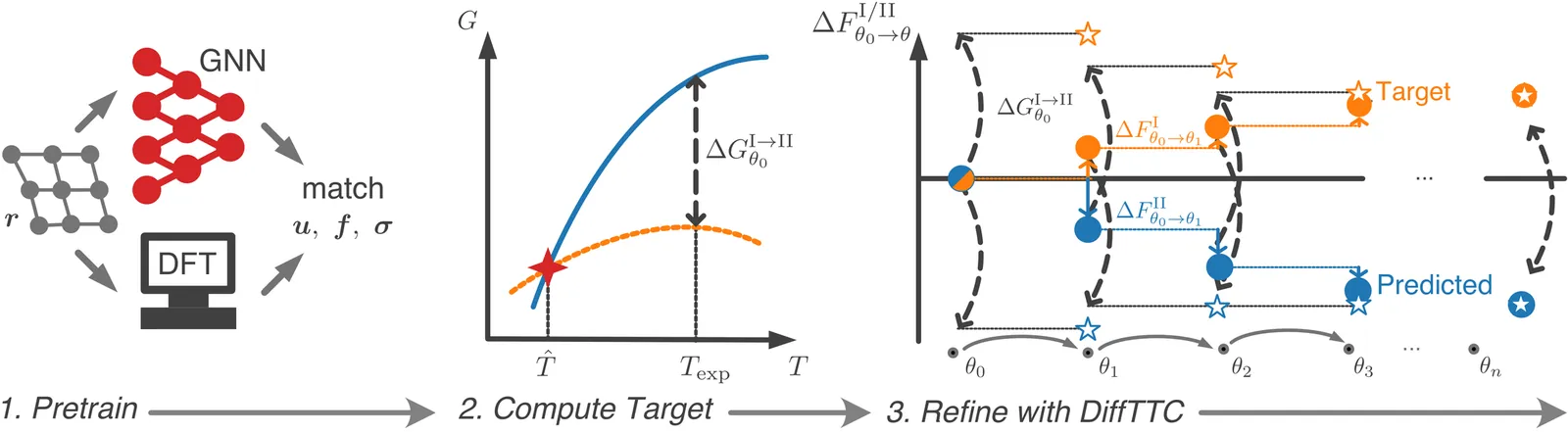
Foundational Machine Learning Potentials can resolve the accuracy and transferability limitations of classical force fields. They enable microscopic insights into material behavior through Molecular Dynamics simulations, which can crucially expedite material design and discovery. However, insufficiently broad and systematically biased reference data affect the predictive quality of the learned models. Often, these models exhibit significant deviations from experimentally observed phase transition temperatures, in the order of several hundred kelvins. Thus, fine-tuning is necessary to achieve adequate accuracy in many practical problems. This work proposes a fine-tuning strategy via top-down learning, directly correcting the wrongly predicted transition temperatures to match the experimental reference data. Our approach leverages the Differentiable Trajectory Reweighting algorithm to minimize the free energy differences between phases at the experimental target pressures and temperatures. We demonstrate that our approach can accurately correct the phase diagram of pure Titanium in a pressure range of up to 5 GPa, matching the experimental reference within tenths of kelvins and improving the liquid-state diffusion constant. Our approach is model-agnostic, applicable to multi-component systems with solid-solid and solid-liquid transitions, and compliant with top-down training on other experimental properties. Therefore, our approach can serve as an essential step towards highly accurate application-specific and foundational machine learning potentials.
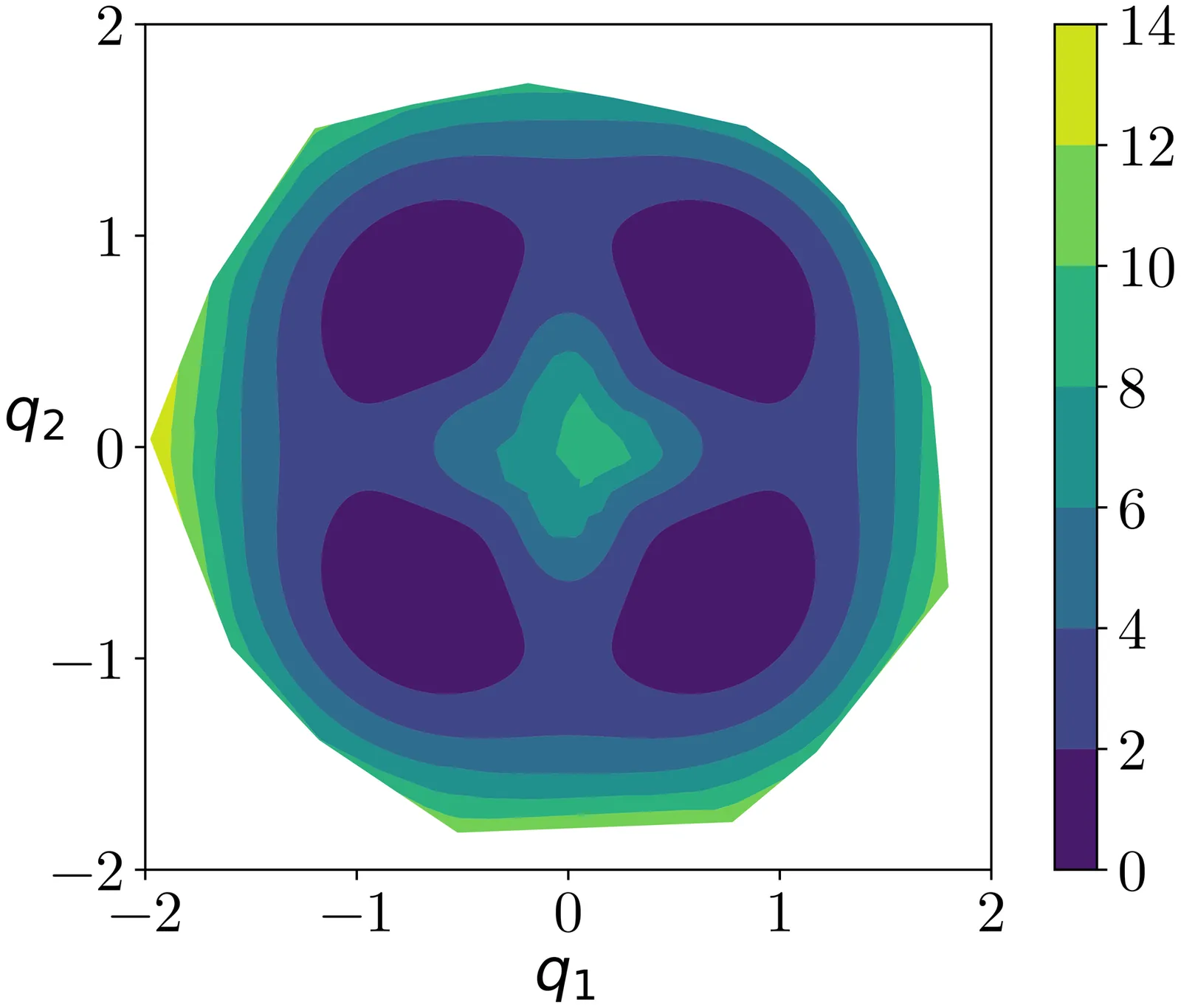
Coarse graining (CG) is an important task for efficient modeling and simulation of complex multi-scale systems, such as the conformational dynamics of biomolecules. This work presents a projection-based coarse-graining formalism for general underdamped Langevin dynamics. Following the Zwanzig projection approach, we derive a closed-form expression for the coarse grained dynamics. In addition, we show how the generator Extended Dynamic Mode Decomposition (gEDMD) method, which was developed in the context of Koopman operator methods, can be used to model the CG dynamics and evaluate its kinetic properties, such as transition timescales. Finally, we combine our approach with thermodynamic interpolation (TI), a generative approach to transform samples between thermodynamic conditions, to extend the scope of the approach across thermodynamic states without repeated numerical simulations. Using a two-dimensional model system, we demonstrate that the proposed method allows to accurately capture the thermodynamic and kinetic properties of the full-space model.