Optimization and Control
arXiv:math.OC
Operations research, linear programming, control theory, systems theory, optimal control, game theory.
Looking for a broader view? This category is part of:
1,685 papers
On the Value Function of Convex Bolza Problems Governed by Stochastic Difference Equations
In this paper we study the value function of Bolza problems governed by stochastic difference equations, with particular emphasis on the convex non-anticipative case. Our goal is to provide some insights on the structure of the subdiferential of the value function. In particular, we establish a connection between the evolution of the subgradients of the value function and a stochastic difference equation of Hamiltonian type. This result can be seen as a transposition of the method of characteristics, introduced by Rockafellar and Wolenski in the 2000s, to the stochastic discrete-time setting. Similarly as done in the literature for the deterministic case, the analysis is based on a duality approach. For this reason we study first a dual representation for the value function in terms of the value function of a dual problem, which is a pseudo Bolza problem. The main difference with the deterministic case is that (due to the non-anticipativity) the symmetry between the Bolza problem and its dual is no longer valid. This in turn implies that ensuring the existence of minimizers for the Bolza problem (which is a key point for establishing the method of characteristics) is not as simple as in the deterministic case, and it should be addressed differently. To complete the exposition, we study the existence of minimizers for a particular class of Bolza problems governed by linear stochastic difference equations, the so-called linear-convex optimal control problems.
2601.05207Jan 2026
View
ZIVR: An Incremental Variance Reduction Technique For Zeroth-Order Composite Problems
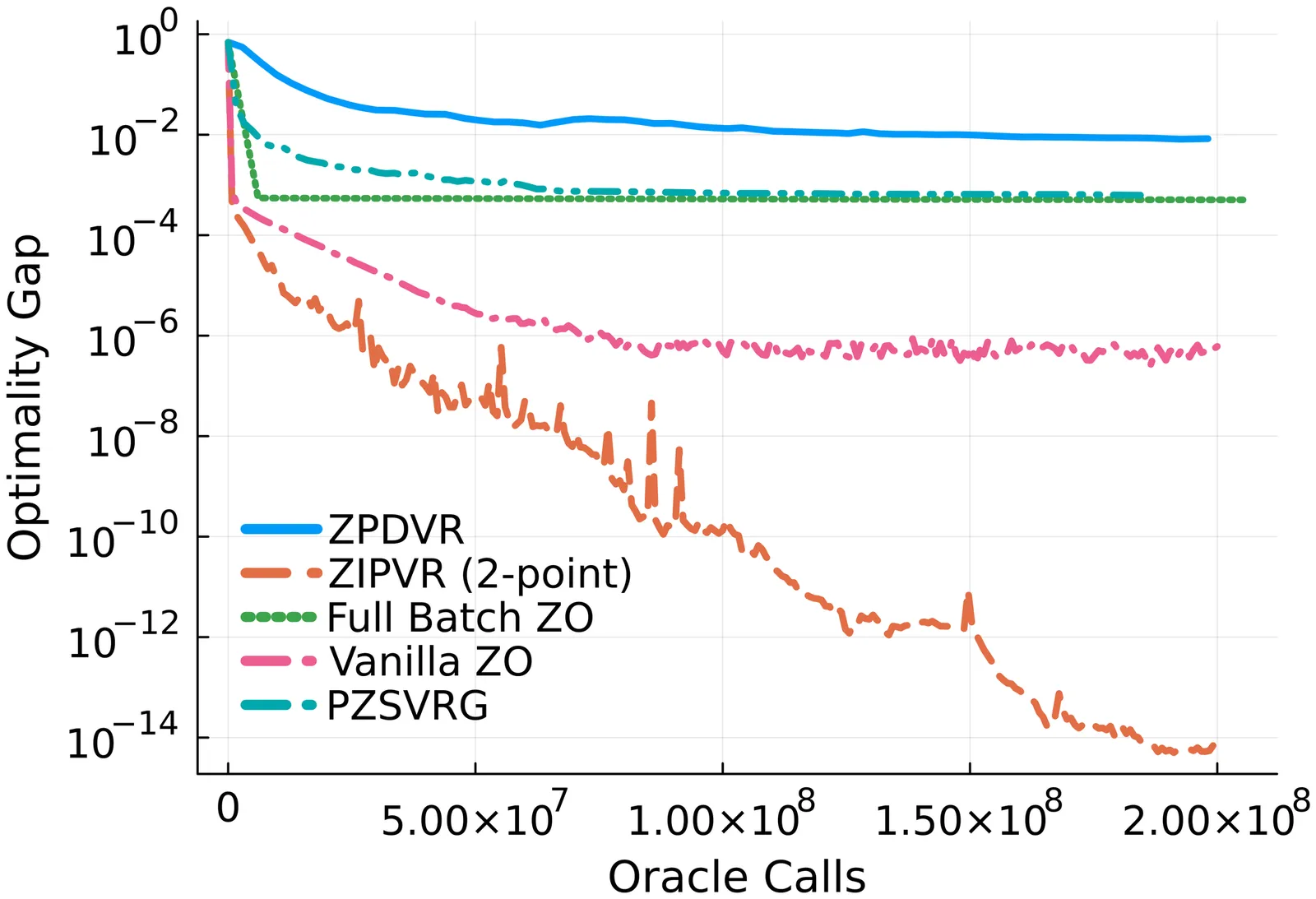
This paper investigates zeroth-order (ZO) finite-sum composite optimization. Recently, variance reduction techniques have been applied to ZO methods to mitigate the non-vanishing variance of 2-point estimators in constrained/composite optimization, yielding improved convergence rates. However, existing ZO variance reduction methods typically involve batch sampling of size at least $Θ(n)$ or $Θ(d)$, which can be computationally prohibitive for large-scale problems. In this work, we propose a general variance reduction framework, Zeroth-Order Incremental Variance Reduction (ZIVR), which supports flexible implementations$\unicode{x2014}$including a pure 2-point zeroth-order algorithm that eliminates the need for large batch sampling. Furthermore, we establish comprehensive convergence guarantees for ZIVR across strongly-convex, convex, and non-convex settings that match their first-order counterparts. Numerical experiments validate the effectiveness of our proposed algorithm.
2601.05056Jan 2026
View
Stochastic convergence of a class of greedy-type algorithms for Configuration Optimization Problems
Greedy Sampling Methods (GSMs) are widely used to construct approximate solutions of Configuration Optimization Problems (COPs), where a loss functional is minimized over finite configurations of points in a compact domain. While effective in practice, deterministic convergence analyses of greedy-type algorithms are often restrictive and difficult to verify. We propose a stochastic framework in which greedy-type methods are formulated as continuous-time Markov processes on the space of configurations. This viewpoint enables convergence analysis in expectation and in probability under mild structural assumptions on the error functional and the transition kernel. For global error functionals, we derive explicit convergence rates, including logarithmic, polynomial, and exponential decay, depending on an abstract improvement condition. As a pedagogical example, we study stochastic greedy sampling for one-dimensional piecewise linear interpolation and prove exponential convergence of the $L^1$-interpolation error for $C^2$-functions. Motivated by this analysis, we introduce the Randomized Polytope Division Method (R-PDM), a randomized variant of the classical Polytope Division Method, and demonstrate its effectiveness and variance reduction in numerical experiments
2601.05029Jan 2026
View
2601.04965Sum of Squares Decompositions and Rank Bounds for Biquadratic Forms
We study positive semi-definite (PSD) biquadratic forms and their sum-of-squares (SOS) representations. For the class of partially symmetric biquadratic forms, we establish necessary and sufficient conditions for positive semi-definiteness and prove that every PSD partially symmetric biquadratic form is a sum of squares of bilinear forms. This extends the known result for fully symmetric biquadratic forms. We describe an efficient computational procedure for constructing SOS decompositions, exploiting the Kronecker-product structure of the associated matrix representation. We present a $2 \times 2$ PSD biquadratic form, and show that it can be expressed as the sum of three squares, but cannot be expressed as the sum of two squares. Furthermore, we present a $3 \times 2$ PSD biquadratic form, and show that it can be expressed as the sum of four squares, but cannot be expressed as the sum of three squares. These show that previously proved results that a $2 \times 2$ PSD biquadratic form can be expressed as the sum of three squares, and a $3 \times 2$ PSD biquadratic form can be expressed as the sum of four squares, are tight.
2601.04965Jan 2026
View
Stochastic Linear-Quadratic Optimal Control Problems with Markovian Regime Switching and $H_\infty$ Constraint under Partial Information
This paper is concerned with a stochastic linear-quadratic optimal control problem of Markovian regime switching system with model uncertainty and partial information, where the information available to the control is based on a sub-$σ$-algebra of the filtration generated by the underlying Brownian motion and the Markov chain. Based on $H_\infty$ control theory, we turn to deal with a soft-constrained zero-sum linear-quadratic stochastic differential game with Markov chain and partial information. By virtue of the filtering technique, the Riccati equation approach, the method of orthogonal decomposition, and the completion-of-squares method, we obtain the closed-loop saddle point of the zero-sum game via the optimal feedback control-strategy pair. Subsequently, we prove that the corresponding outcome of the closed-loop saddle point satisfies the $H_\infty$ performance criterion. Finally, the obtained theoretical results are applied to a stock market investment problem to further illustrate the practical significance and effectiveness.
2601.04652Jan 2026
View
A Single-Loop Bilevel Deep Learning Method for Optimal Control of Obstacle Problems
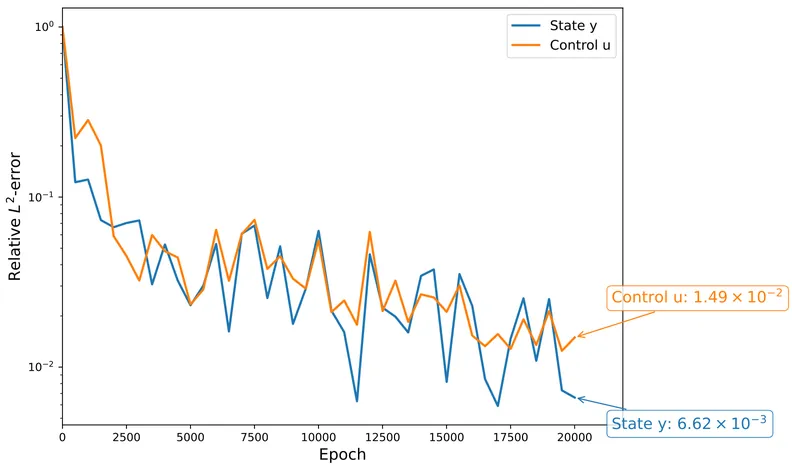
Optimal control of obstacle problems arises in a wide range of applications and is computationally challenging due to its nonsmoothness, nonlinearity, and bilevel structure. Classical numerical approaches rely on mesh-based discretization and typically require solving a sequence of costly subproblems. In this work, we propose a single-loop bilevel deep learning method, which is mesh-free, scalable to high-dimensional and complex domains, and avoids repeated solution of discretized subproblems. The method employs constraint-embedding neural networks to approximate the state and control and preserves the bilevel structure. To train the neural networks efficiently, we propose a Single-Loop Stochastic First-Order Bilevel Algorithm (S2-FOBA), which eliminates nested optimization and does not rely on restrictive lower-level uniqueness assumptions. We analyze the convergence behavior of S2-FOBA under mild assumptions. Numerical experiments on benchmark examples, including distributed and obstacle control problems with regular and irregular obstacles on complex domains, demonstrate that the proposed method achieves satisfactory accuracy while reducing computational cost compared to classical numerical methods.
2601.04120Jan 2026
View
Continuation methods for higher-order topology optimization
We aim to solve a topology optimization problem where the distribution of material in the design domain is represented by a density function. To obtain candidates for local minima, we want to solve the first order optimality system via Newton's method. This requires the initial guess to be sufficiently close to the a priori unknown solution. Introducing a stepsize rule often allows for less restrictions on the initial guess while still preserving convergence. In topology optimization one typically encounters nonconvex problems where this approach might fail. We therefore opt for a homotopy (continuation) approach which is based on solving a sequence of parametrized problems to approach the solution of the original problem. In the density based framework the values of the design variable are constrained by 0 from below and 1 from above. Coupling the homotopy method with a barrier strategy enforces these constraints to be satisified. The numerical results for a PDE-constrained compliance minimization problem demonstrate that this combined approach maintains feasibility of the density function and converges to a (candidate for a) locally optimal design without a priori knowledge of the solution.
2601.04003Jan 2026
View
Provably Finding a Hidden Dense Submatrix among Many Planted Dense Submatrices via Convex Programming
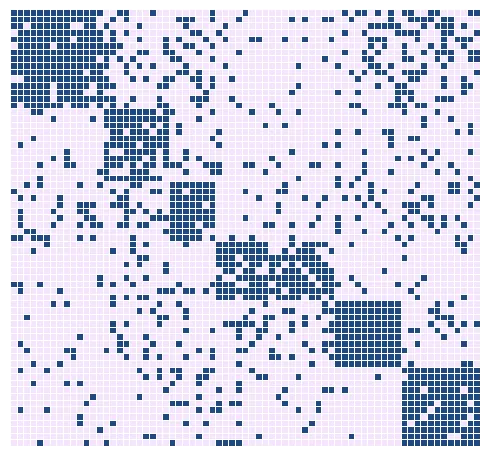
We consider the densest submatrix problem, which seeks the submatrix of fixed size of a given binary matrix that contains the most nonzero entries. This problem is a natural generalization of fundamental problems in combinatorial optimization, e.g., the densest subgraph, maximum clique, and maximum edge biclique problems, and has wide application the study of complex networks. Much recent research has focused on the development of sufficient conditions for exact solution of the densest submatrix problem via convex relaxation. The vast majority of these sufficient conditions establish identification of the densest submatrix within a graph containing exactly one large dense submatrix hidden by noise. The assumptions of these underlying models are not observed in real-world networks, where the data may correspond to a matrix containing many dense submatrices of varying sizes. We extend and generalize these results to the more realistic setting where the input matrix may contain \emph{many} large dense subgraphs. Specifically, we establish sufficient conditions under which we can expect to solve the densest submatrix problem in polynomial time for random input matrices sampled from a generalization of the stochastic block model. Moreover, we also provide sufficient conditions for perfect recovery under a deterministic adversarial. Numerical experiments involving randomly generated problem instances and real-world collaboration and communication networks are used empirically to verify the theoretical phase-transitions to perfect recovery given by these sufficient conditions.
2601.03946Jan 2026
View2601.03759Connecting Max-entropy With Computational Geometry, LP And SDP
We consider the well-known max-(relative) entropy problem $Θ$(y) = infQ$\ll$P DKL(Q P ) with Kullback-Leibler divergence on a domain $Ω$ $\subset$ R d , and with ''moment'' constraints h dQ = y, y $\in$ R m . We show that when m $\le$ d, $Θ$ is the Cram{é}r transform of a function v that solves a simply related computational geometry problem. Also, and remarkably, to the canonical LP: min x$\ge$0 {c T x\,: A x = y}, with A $\in$ R mxd , one may associate a max-entropy problem with a suitably chosen reference measure P on R d + and linear mapping h(x) = Ax, such that its associated perspective function $ε$ $Θ$(y/$ε$) is the optimal value of the log-barrier formulation (with parameter $ε$) of the dual LP (and so it converges to the LP optimal value as $ε$ $\rightarrow$ 0). An analogous result also holds for the canonical SDP: min X 0 { C, X\,: A(X) = y }.
2601.03759Jan 2026
View
GPU-Accelerated Cholesky Factorization of Block Tridiagonal Matrices
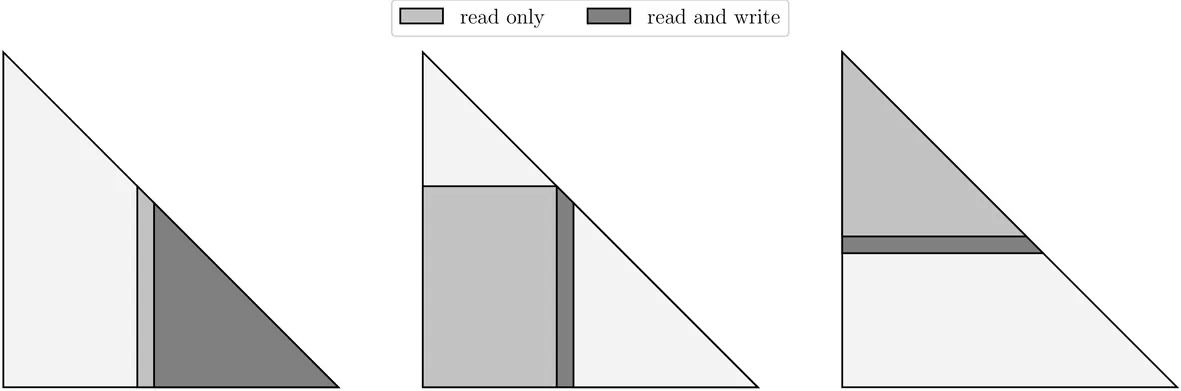
This paper presents a GPU-accelerated framework for solving block tridiagonal linear systems that arise naturally in numerous real-time applications across engineering and scientific computing. Through a multi-stage permutation strategy based on nested dissection, we reduce the computational complexity from $\mathcal{O}(Nn^3)$ for sequential Cholesky factorization to $\mathcal{O}(\log_2(N)n^3)$ when sufficient parallel resources are available, where $n$ is the block size and $N$ is the number of blocks. The algorithm is implemented using NVIDIA's Warp library and CUDA to exploit parallelism at multiple levels within the factorization algorithm. Our implementation achieves speedups exceeding 100x compared to the sparse solver QDLDL, 25x compared to a highly optimized CPU implementation using BLASFEO, and more than 2x compared to NVIDIA's CUDSS library. The logarithmic scaling with horizon length makes this approach particularly attractive for long-horizon problems in real-time applications. Comprehensive numerical experiments on NVIDIA GPUs demonstrate the practical effectiveness across different problem sizes and precisions. The framework provides a foundation for GPU-accelerated optimization solvers in robotics, autonomous systems, and other domains requiring repeated solution of structured linear systems. The implementation is open-source and available at https://github.com/PREDICT-EPFL/socu.
2601.03754Jan 2026
View2601.03747Matrix Riccati BSDEs with singular terminal condition and stochastic LQ control with linear terminal constraint
We analyze a class of multidimensional linear-quadratic stochastic control problems with random coefficients, motivated by multi-asset optimal trade execution. The problems feature non-diffusive controlled state dynamics and a terminal constraint that restricts the terminal state to a prescribed random linear subspace. We derive the associated Riccati backward stochastic differential equation (BSDE) and identify a suitable formalization of its singular terminal condition. Via a penalization approach, we establish existence of a minimal supersolution of the Riccati BSDE and use it to characterize both the value function and the optimal control. We analyze the asymptotic behavior of the supersolution near terminal time and discuss special cases where closed-form solutions can be obtained.
2601.03747Jan 2026
View
Provably Convergent Decentralized Optimization over Directed Graphs under Generalized Smoothness
Decentralized optimization has become a fundamental tool for large-scale learning systems; however, most existing methods rely on the classical Lipschitz smoothness assumption, which is often violated in problems with rapidly varying gradients. Motivated by this limitation, we study decentralized optimization under the generalized $(L_0, L_1)$-smoothness framework, in which the Hessian norm is allowed to grow linearly with the gradient norm, thereby accommodating rapidly varying gradients beyond classical Lipschitz smoothness. We integrate gradient-tracking techniques with gradient clipping and carefully design the clipping threshold to ensure accurate convergence over directed communication graphs under generalized smoothness. In contrast to existing distributed optimization results under generalized smoothness that require a bounded gradient dissimilarity assumption, our results remain valid even when the gradient dissimilarity is unbounded, making the proposed framework more applicable to realistic heterogeneous data environments. We validate our approach via numerical experiments on standard benchmark datasets, including LIBSVM and CIFAR-10, using regularized logistic regression and convolutional neural networks, demonstrating superior stability and faster convergence over existing methods.
2601.03566Jan 2026
View2601.03333Optimal Quantization of Finite Uniform Data on the Sphere
This paper develops a systematic and geometric theory of optimal quantization on the unit sphere $\mathbb S^2$, focusing on finite uniform probability distributions supported on the spherical surface - rather than on lower-dimensional geodesic subsets such as circles or arcs. We first establish the existence of optimal sets of $n$-means and characterize them through centroidal spherical Voronoi tessellations. Three fundamental structural results are obtained. First, a cluster - purity theorem shows that when the support consists of well-separated components, each optimal Voronoi region remains confined to a single component. Second, a ring - allocation (discrete water - filling) theorem provides an explicit rule describing how optimal representatives are distributed across multiple latitudinal rings, together with closed-form distortion formulas. Third, a Lipschitz - type stability theorem quantifies the robustness of optimal configurations under small geodesic perturbations of the support. In addition, a spherical analogue of Lloyd's algorithm is presented, in which intrinsic (Karcher) means replace Euclidean centroids for iterative refinement. These results collectively provide a unified and transparent framework for understanding the geometric and algorithmic structure of optimal quantization on $\mathbb S^2$.
2601.03333Jan 2026
View
Adaptive Control of Unknown Linear Switched Systems via Policy Gradient Methods
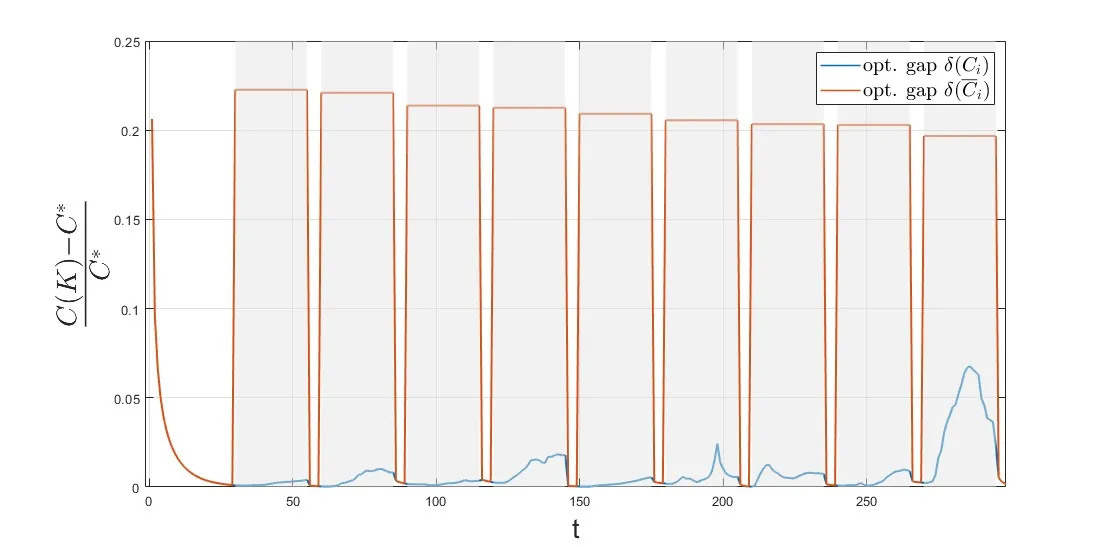
We consider the policy gradient adaptive control (PGAC) framework, which adaptively updates a control policy in real time, by performing data-based gradient descent steps on the linear quadratic regulator cost. This method has empirically shown to react to changing circumstances, such as model parameters, efficiently. To formalize this observation, we design a PGAC method which stabilizes linear switched systems, where both model parameters and switching time are unknown. We use sliding window data for the policy gradient estimate and show that under a dwell time condition and small dynamics variation, the policy can track the switching dynamics and ensure closed-loop stability. We perform simulations to validate our theoretical results.
2601.03016Jan 2026
View
An overview of the fractional-order gradient descent method and its applications
Recent studies have shown that fractional calculus is an effective alternative mathematical tool in various scientific fields. However, some investigations indicate that results established in differential and integral calculus do not necessarily hold true in fractional calculus. In this work we will compare various methods presented in the literature to improve the Gradient Descent Method, in terms of convergence of the method, convergence to the extreme point, and convergence rate. In general, these methods that generalize the gradient descent algorithm by replacing the gradient with a fractional-order operator are inefficient in achieving convergence to the extremum point of the objective function. To avoid these difficulties, we proposed to choose the Fractional Continuous Time algorithm to generalize the gradient method. In this approach, the convergence of the method to the extreme point of the function is guaranteed by introducing the fractional order in the time derivative, rather than in of the gradient. In this case, the issue of finding the extreme point is resolved, while the issue of stability at the equilibrium point remains. Fractional Continuous Time method converges to extreme point of cost function when fractional-order is between 0 and 1. The simulations shown in this work suggests that a similar result can be found when $1 \leq α\leq 2$. { This paper highlights the main advantages and disadvantages of generalizations of the gradient method using fractional derivatives, aiming to optimize convergence in complex problems. Some chemical problems, with n=11 and 24 optimization parameters, are employed as means of evaluating the efficacy of the propose algorithms. In general, previous studies are restricted to mathematical questions and simple illustrative examples.
2601.03318Jan 2026
View
A Relaxation Method for Nonsmooth Nonlinear Optimization with Binary Constraints
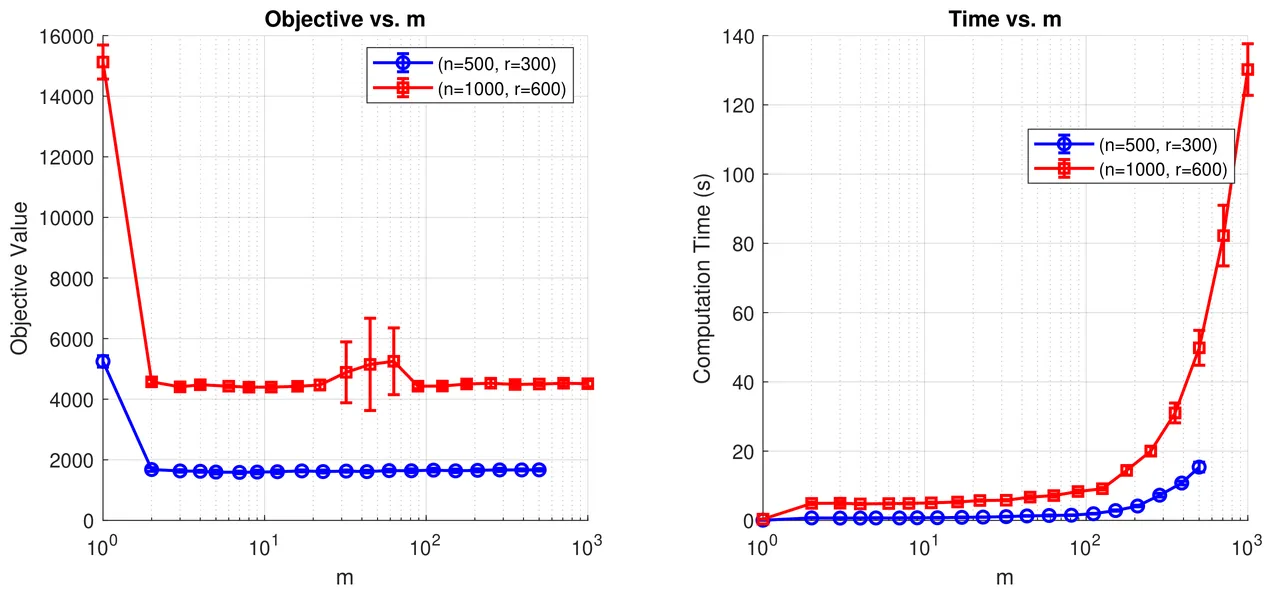
We study binary optimization problems of the form \( \min_{x\in\{-1,1\}^n} f(Ax-b) \) with possibly nonsmooth loss \(f\). Following the lifted rank-one semidefinite programming (SDP) approach\cite{qian2023matrix}, we develop a majorization-minimization algorithm by using the difference-of-convexity (DC) reformuation for the rank-one constraint and the Moreau envelop for the nonsmooth loss. We provide global complexity guarantees for the proposed \textbf{D}ifference of \textbf{C}onvex \textbf{R}elaxation \textbf{A}lgorithm (DCRA) and show that it produces an approximately feasible binary solution with an explicit bound on the optimality gap. Numerical experiments on synthetic and real datasets confirm that our method achieves superior accuracy and scalability compared with existing approaches.
2601.03008Jan 2026
View2601.02951Hopfield neural networks as port-Hamiltonian and gradient systems
The structure of continuous Hopfield networks is revisited from a system-theoretic point of view. After adopting a novel electrical network interpretation involving nonlinear capacitors, it is shown that Hopfield networks admit a port-Hamiltonian formulation provided an extra passivity condition is satisfied. Subsequently it is shown that any Hopfield network can be represented as a gradient system, with Riemannian metric given by the inverse of the Hessian matrix of the total energy stored in the nonlinear capacitors. On the other hand, the well-known 'energy' function employed by Hopfield turns out to be the dissipation potential of the gradient system, and this potential is shown to satisfy a dissipation inequality that can be used for analysis and interconnection.
2601.02951Jan 2026
View2601.02899Relating Checkpoint Update Probabilities to Momentum Parameters in Single-Loop Variance Reduction Methods
Variance reduction (VR) is a crucial tool for solving finite-sum optimization problems, including the composite general convex setting, which is the focus of this work. On the one hand, denoting the number of component functions as $n$ and the target accuracy as $ε$, some VR methods achieve the near-optimal complexity $\widetilde{\mathcal{O}}\left(n+\sqrt{n}/\sqrtε\right)$, but they all have nested structure and fail to provide convergence guarantee for the iterate sequence itself. On the other hand, single-loop VR methods, being free from the aforementioned disadvantages, have complexity no better than $\mathcal{O}\left(n+n/\sqrtε\right)$ which is the complexity of the deterministic method FISTA, thus leaving a critical gap unaddressed. In this work, we propose the \textit{Harmonia} technique which relates checkpoint update probabilities to momentum parameters in single-loop VR methods. Based on this technique, we further propose to vary the growth rate of the momentum parameter, creating a novel continuous trade-off between acceleration and variance reduction, controlled by the key parameter $α\in[0,1]$. The proposed techniques lead to following favourable consequences. First, several known complexity of quite different algorithms are re-discovered under the proposed unifying algorithmic framework Katyusha-H. Second, under an extra mild condition, Katyusha-H achieves the near-optimal complexity for $α$ belonging to a certain interval, highlighting the effectiveness of the acceleration-variance reduction trade-off. Last, without extra conditions, Katyusha-H achieves the complexity $\widetilde{\mathcal{O}}(n+\sqrt{n}/\sqrtε)$ with $α=1$ and proper mini-batch sizes. The proposed idea and techniques may be of general interest beyond the considered problem in this work.
2601.02899Jan 2026
View2601.02797Log-Polynomial Optimization
We study an optimization problem in which the objective is given as a sum of logarithmic-polynomial functions. This formulation is motivated by statistical estimation principles such as maximum likelihood estimation, and by loss functions including cross-entropy and Kullback-Leibler divergence. We propose a hierarchy of moment relaxations based on the truncated $K$-moment problems to solve log-polynomial optimization. We provide sufficient conditions for the hierarchy to be tight and introduce a numerical method to extract the global optimizers when the tightness is achieved. In addition, we modify relaxations with optimality conditions to better fit log-polynomial optimization with convenient Lagrange multipliers expressions. Various applications and numerical experiments are presented to show the efficiency of our method.
2601.02797Jan 2026
View
Adapting Polyhedral Dominance Cones to Ordinal Preference Structures
In combinatorial optimization, ordinal costs can be used to model the quality of elements whenever numerical values are not available. When considering, for example, routing problems for cyclists, the safety of a street can be ranked in ordered categories like safe (separate bike lane), medium safe (street with a bike lane) and unsafe (street without a bike lane). However, ordinal optimization may suggest unrealistic solutions with huge detours to avoid unsafe street segments. In this paper, we investigate how partial preference information regarding the relative quality of the ordinal categories can be used to improve the relevance of the computed solutions. By introducing preference weights which describe how much better a category is at least or at most, compared to the subsequent category, we enlarge the ordinal dominance cone. This leads to a smaller set of alternatives, i. e., of ordinally efficient solutions. We show that the corresponding weighted ordinal ordering cone is a polyhedral cone and provide descriptions via its extreme rays and via its facets. The latter implies a linear transformation to an associated multi-objective optimization problem. This paves the way for the application of standard multi-objective solution approaches. We demonstrate the usefulness of the weighted ordinal ordering cone by investigating a safest path problem with different preference weights. Moreover, we investigate the interrelation between the weighted ordering cone to standard dominance concepts of multi-objective optimization, like, e.g., Pareto dominance, lexicographic dominance and weighted sum dominance.
2601.02796Jan 2026
ViewPage 1 of 85
