Risk Management
Measurement and management of financial risks in trading, currentrency, banking.
Measurement and management of financial risks in trading, currentrency, banking.
Machine learning improves predictive accuracy in insurance pricing but exacerbates trade-offs between competing fairness criteria across different discrimination measures, challenging regulators and insurers to reconcile profitability with equitable outcomes. While existing fairness-aware models offer partial solutions under GLM and XGBoost estimation methods, they remain constrained by single-objective optimization, failing to holistically navigate a conflicting landscape of accuracy, group fairness, individual fairness, and counterfactual fairness. To address this, we propose a novel multi-objective optimization framework that jointly optimizes all four criteria via the Non-dominated Sorting Genetic Algorithm II (NSGA-II), generating a diverse Pareto front of trade-off solutions. We use a specific selection mechanism to extract a premium on this front. Our results show that XGBoost outperforms GLM in accuracy but amplifies fairness disparities; the Orthogonal model excels in group fairness, while Synthetic Control leads in individual and counterfactual fairness. Our method consistently achieves a balanced compromise, outperforming single-model approaches.
We propose a novel framework for risk-sensitive reinforcement learning (RSRL) that incorporates robustness against transition uncertainty. We define two distinct yet coupled risk measures: an inner risk measure addressing state and cost randomness and an outer risk measure capturing transition dynamics uncertainty. Our framework unifies and generalizes most existing RL frameworks by permitting general coherent risk measures for both inner and outer risk measures. Within this framework, we construct a risk-sensitive robust Markov decision process (RSRMDP), derive its Bellman equation, and provide error analysis under a given posterior distribution. We further develop a Bayesian Dynamic Programming (Bayesian DP) algorithm that alternates between posterior updates and value iteration. The approach employs an estimator for the risk-based Bellman operator that combines Monte Carlo sampling with convex optimization, for which we prove strong consistency guarantees. Furthermore, we demonstrate that the algorithm converges to a near-optimal policy in the training environment and analyze both the sample complexity and the computational complexity under the Dirichlet posterior and CVaR. Finally, we validate our approach through two numerical experiments. The results exhibit excellent convergence properties while providing intuitive demonstrations of its advantages in both risk-sensitivity and robustness. Empirically, we further demonstrate the advantages of the proposed algorithm through an application on option hedging.
Financial crises emerge when structural vulnerabilities accumulate across sectors, markets, and investor behavior. Predicting these systemic transitions is challenging because they arise from evolving interactions between market participants, not isolated price movements alone. We present Systemic Risk Radar (SRR), a framework that models financial markets as multi-layer graphs to detect early signs of systemic fragility and crash-regime transitions. We evaluate SRR across three major crises: the Dot-com crash, the Global Financial Crisis, and the COVID-19 shock. Our experiments compare snapshot GNNs, a simplified temporal GNN prototype, and standard baselines (logistic regression and Random Forest). Results show that structural network information provides useful early-warning signals compared to feature-based models alone. This correlation-based instantiation of SRR demonstrates that graph-derived features capture meaningful changes in market structure during stress events. The findings motivate extending SRR with additional graph layers (sector/factor exposure, sentiment) and more expressive temporal architectures (LSTM/GRU or Transformer encoders) to better handle diverse crisis types.
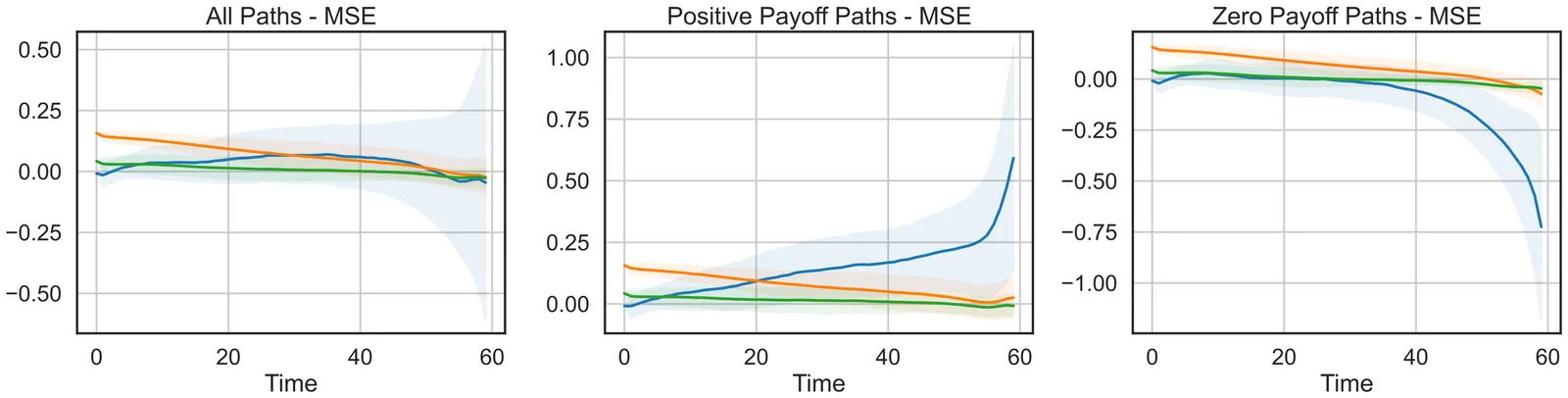
This paper investigates the deep hedging framework, based on reinforcement learning (RL), for the dynamic hedging of swaptions, contrasting its performance with traditional sensitivity-based rho-hedging. We design agents under three distinct objective functions (mean squared error, downside risk, and Conditional Value-at-Risk) to capture alternative risk preferences and evaluate how these objectives shape hedging styles. Relying on a three-factor arbitrage-free dynamic Nelson-Siegel model for our simulation experiments, our findings show that near-optimal hedging effectiveness is achieved when using two swaps as hedging instruments. Deep hedging strategies dynamically adapt the hedging portfolio's exposure to risk factors across states of the market. In our experiments, their out-performance over rho-hedging strategies persists even in the presence some of model misspecification. These results highlight RL's potential to deliver more efficient and resilient swaption hedging strategies.
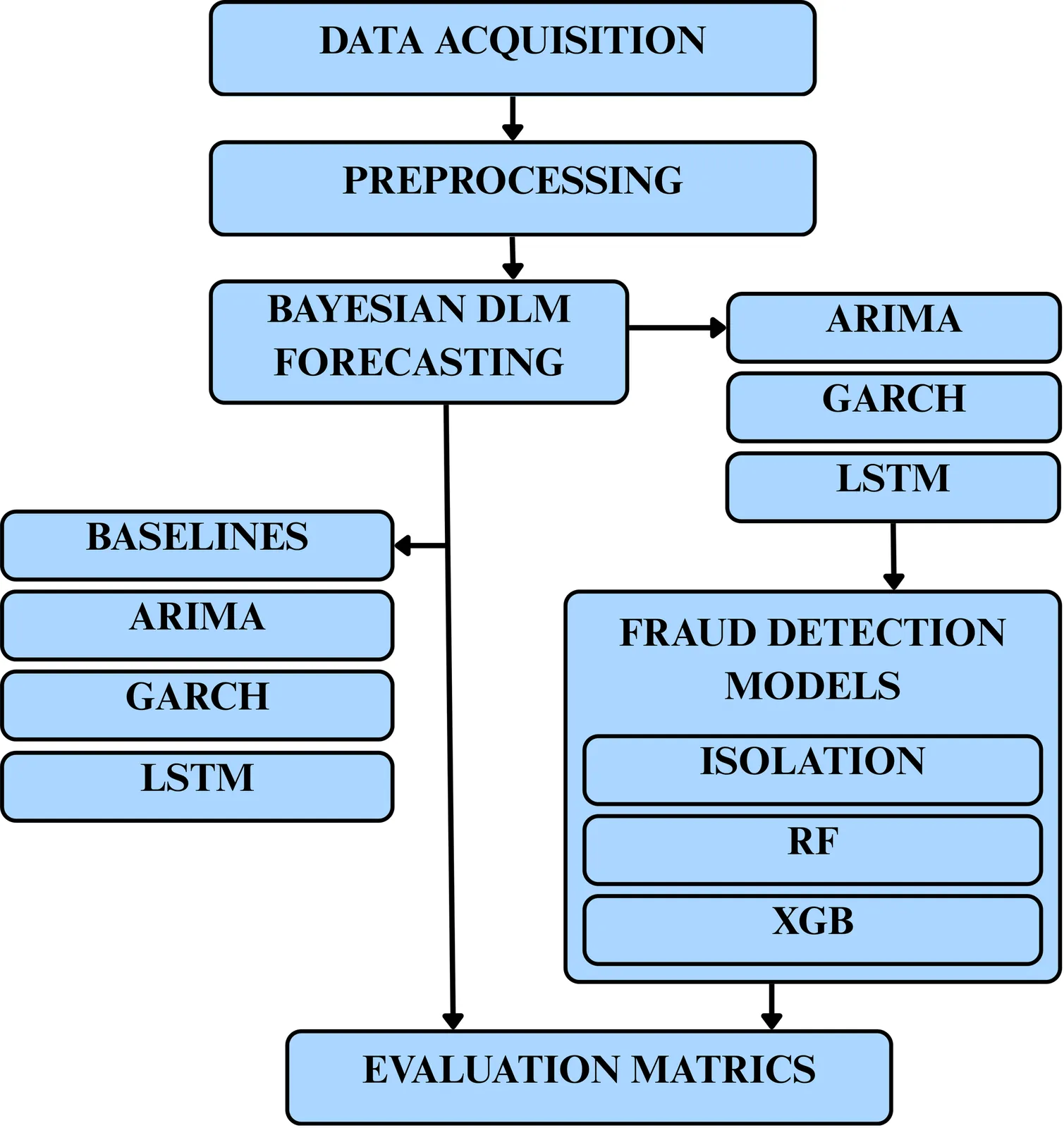
A Bayesian analytics framework that precisely quantifies uncertainty offers a significant advance for financial risk management. We develop an integrated approach that consistently enhances the handling of risk in market volatility forecasting, fraud detection, and compliance monitoring. Our probabilistic, interpretable models deliver reliable results: We evaluate the performance of one-day-ahead 95% Value-at-Risk (VaR) forecasts on daily S&P 500 returns, with a training period from 2000 to 2019 and an out-of-sample test period spanning 2020 to 2024. Formal tests of unconditional (Kupiec) and conditional (Christoffersen) coverage reveal that an LSTM baseline achieves near-nominal calibration. In contrast, a GARCH(1,1) model with Student-t innovations underestimates tail risk. Our proposed discount-factor DLM model produces a slightly liberal VaR estimate, with evidence of clustered violations. Bayesian logistic regression improves recall and AUC-ROC for fraud detection, and a hierarchical Beta state-space model provides transparent and adaptive compliance risk assessment. The pipeline is distinguished by precise uncertainty quantification, interpretability, and GPU-accelerated analysis, delivering up to 50x speedup. Remaining challenges include sparse fraud data and proxy compliance labels, but the framework enables actionable risk insights. Future expansion will extend feature sets, explore regime-switching priors, and enhance scalable inference.
 2512.03267
2512.03267In financial and actuarial research, distortion and Haezendonck-Goovaerts risk measures are attractive due to their strong properties. They have so far been treated separately. In this paper, following a suggestion by Goovaerts, Linders, Van Weert, and Tank, we introduce and study a new class of risk measure that encompasses the distortion and Haezendonck-Goovaerts risk measures, aptly called the distortion Haezendonck-Goovaerts risk measures. They will be defined on a larger space than the space of bounded risks. We provide situations where these new risk measures are coherent, and explore their risk theoretic properties.
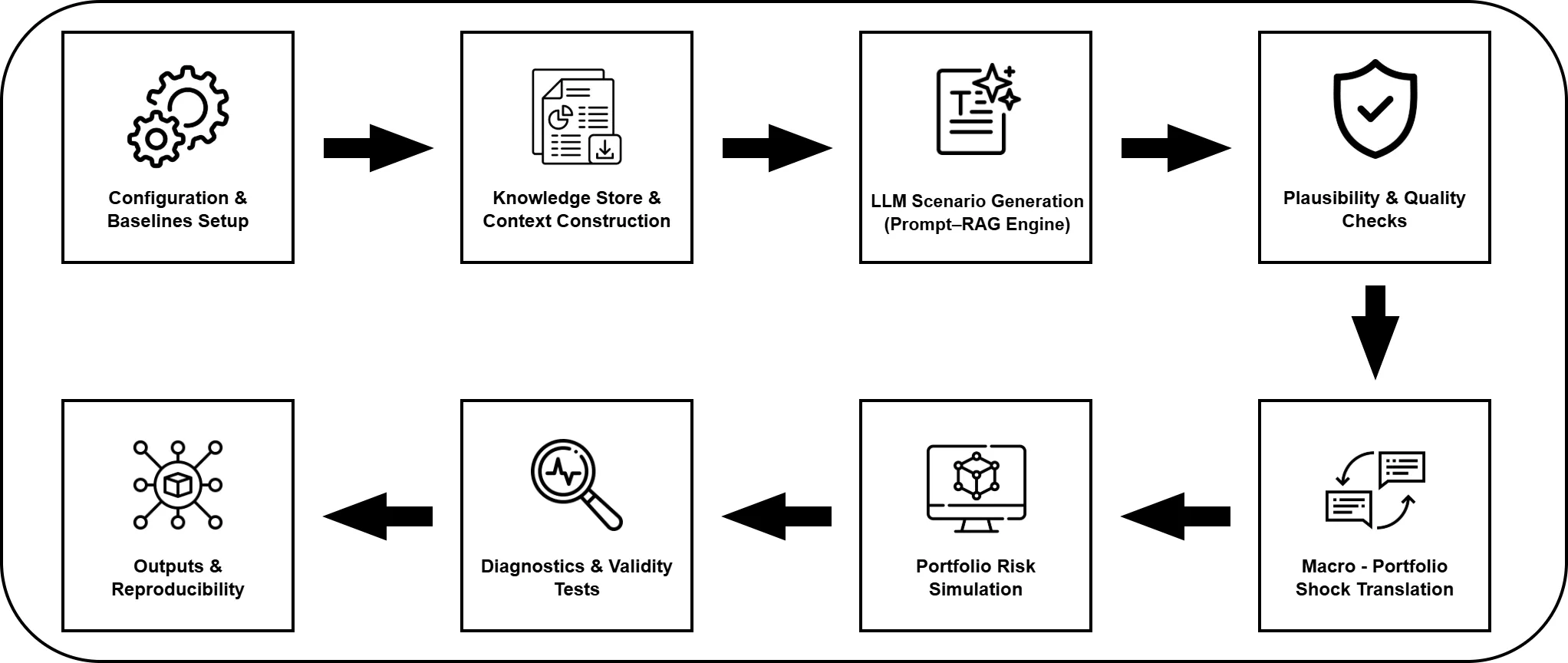
We develop a transparent and fully auditable LLM-based pipeline for macro-financial stress testing, combining structured prompting with optional retrieval of country fundamentals and news. The system generates machine-readable macroeconomic scenarios for the G7, which cover GDP growth, inflation, and policy rates, and are translated into portfolio losses through a factor-based mapping that enables Value-at-Risk and Expected Shortfall assessment relative to classical econometric baselines. Across models, countries, and retrieval settings, the LLMs produce coherent and country-specific stress narratives, yielding stable tail-risk amplification with limited sensitivity to retrieval choices. Comprehensive plausibility checks, scenario diagnostics, and ANOVA-based variance decomposition show that risk variation is driven primarily by portfolio composition and prompt design rather than by the retrieval mechanism. The pipeline incorporates snapshotting, deterministic modes, and hash-verified artifacts to ensure reproducibility and auditability. Overall, the results demonstrate that LLM-generated macro scenarios, when paired with transparent structure and rigorous validation, can provide a scalable and interpretable complement to traditional stress-testing frameworks.
 2511.18169
2511.18169We revisit the well-studied superhedging problem under proportional transaction costs in continuous time using the recently developed tools of set-valued stochastic analysis. By relying on a simple Black-Scholes-type market model for mid-prices and using continuous trading schemes, we define a dynamic family of superhedging sets in continuous time and express them in terms of set-valued integrals. We show that these sets, defined as subsets of Lebesgue spaces at different times, form a dynamic set-valued risk measure with multi-portfolio time-consistency. Finally, we transfer the problem formulation to a path-space setting and introduce approximate versions of superhedging sets that will involve relaxing the superhedging inequality, the superhedging probability, and the solvency requirement for the superhedging strategy with a predetermined error level. In this more technical framework, we are able to relate the approximate superhedging sets at different times by means of a set-valued Bellman's principle, which we believe will pave the way for a set-valued differential structure that characterizes the superhedging sets.
Incorporating spatial information, particularly those influenced by climate, weather, and demographic factors, is crucial for improving underwriting precision and enhancing risk management in insurance. However, spatial data are often unstructured, high-dimensional, and difficult to integrate into predictive models. Embedding methods are needed to convert spatial data into meaningful representations for modelling tasks. We propose a novel multi-view contrastive learning framework for generating spatial embeddings that combine information from multiple spatial data sources. To train the model, we construct a spatial dataset that merges satellite imagery and OpenStreetMap features across Europe. The framework aligns these spatial views with coordinate-based encodings, producing low-dimensional embeddings that capture both spatial structure and contextual similarity. Once trained, the model generates embeddings directly from latitude-longitude pairs, enabling any dataset with coordinates to be enriched with meaningful spatial features without requiring access to the original spatial inputs. In a case study on French real estate prices, we compare models trained on raw coordinates against those using our spatial embeddings as inputs. The embeddings consistently improve predictive accuracy across generalised linear, additive, and boosting models, while providing interpretable spatial effects and demonstrating transferability to unseen regions.
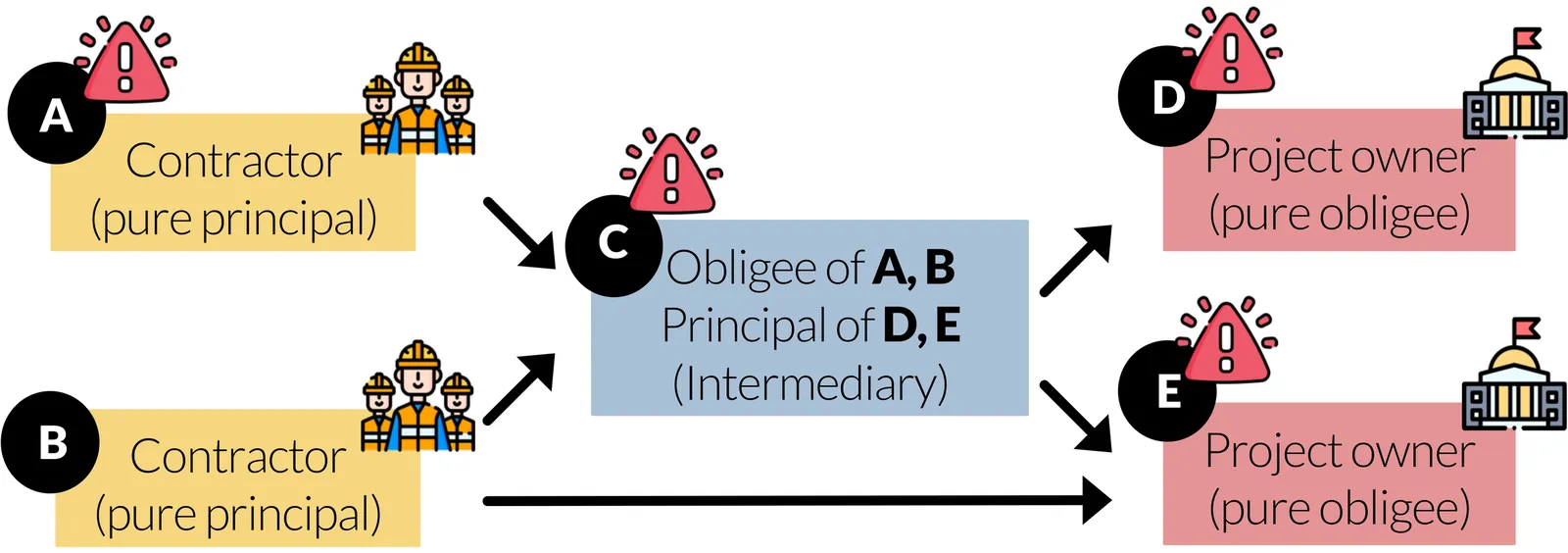
Surety bonds are financial agreements between a contractor (principal) and obligee (project owner) to complete a project. However, most large-scale projects involve multiple contractors, creating a network and introducing the possibility of incomplete obligations to propagate and result in project failures. Typical models for risk assessment assume independent failure probabilities within each contractor. However, we take a network approach, modeling the contractor network as a directed graph where nodes represent contractors and project owners and edges represent contractual obligations with associated financial records. To understand risk propagation throughout the contractor network, we extend the celebrated Friedkin-Johnsen model and introduce a stochastic process to simulate principal failures across the network. From a theoretical perspective, we show that under natural monotonicity conditions on the contractor network, incorporating network effects leads to increases in both the average risk and the tail probability mass of the loss distribution (i.e. larger right-tail risk) for the surety organization. We further use data from a partnering insurance company to validate our findings, estimating an approximately 2% higher exposure when accounting for network effects.
The calculation of the insurance liabilities of a cohort of dependent individuals in general requires the solution of a high-dimensional system of coupled linear forward integro-differential equations, which is infeasible for a larger cohort. However, by using a mean-field approximation, the high dimensional system of linear forward equations can be replaced by a low-dimensional system of non-linear forward integro-differential equations. We show that, subject to certain regularity conditions, the insurance liability viewed as a (conditional) expectation of a functional of an underlying jump process converges to its mean-field approximation, as the number of individuals in the cohort goes to infinity. Examples from both life- and non-life insurance illuminate the practical importance of mean-field approximations.
 2511.07431
2511.07431Design and implementation of appropriate social protection strategies is one of the main targets of the United Nation's Sustainable Development Goal (SDG) 1: No Poverty. Cash transfer (CT) programmes are considered one of the main social protection strategies and an instrument for achieving SDG 1. Targeting consists of establishing eligibility criteria for beneficiaries of CT programmes. In low-income countries, where resources are limited, proper targeting of CTs is essential for an efficient use of resources. Given the growing importance of microinsurance as a complementary tool to social protection strategies, this study examines its role as a supplement to CT programmes. In this article, we adopt the piecewise-deterministic Markov process introduced in Kovacevic and Pflug (2011) to model the capital of a household, which when exposed to large proportional capital losses (in contrast to the classical Cramér-Lundberg model) can push them into the poverty area. Striving for cost-effective CT programmes, we optimise the expected discounted cost of keeping the household's capital above the poverty line by means of injection of capital (as a direct capital transfer). Using dynamic programming techniques, we derive the Hamilton-Jacobi-Bellman (HJB) equation associated with the optimal control problem of determining the amount of capital to inject over time. We show that this equation admits a viscosity solution that can be approximated numerically. Moreover, in certain special cases, we obtain closed-form expressions for the solution. Numerical examples show that there is an optimal level of injection above the poverty threshold, suggesting that efficient use of resources is achieved when CTs are preventive rather than reactive, since injecting capital into households when their capital levels are above the poverty line is less costly than to do so only when it falls below the threshold.
 2510.05809
2510.05809We develop a statistical framework for risk estimation, inspired by the axiomatic theory of risk measures. Coherent risk estimators -- functionals of P&L samples inheriting the economic properties of risk measures -- are defined and characterized through robust representations linked to $L$-estimators. The framework provides a canonical methodology for constructing estimators with sound financial and statistical properties, unifying risk measure theory, principles for capital adequacy, and practical statistical challenges in market risk. A numerical study illustrates the approach, focusing on expected shortfall estimation under both i.i.d. and overlapping samples relevant for regulatory FRTB model applications.
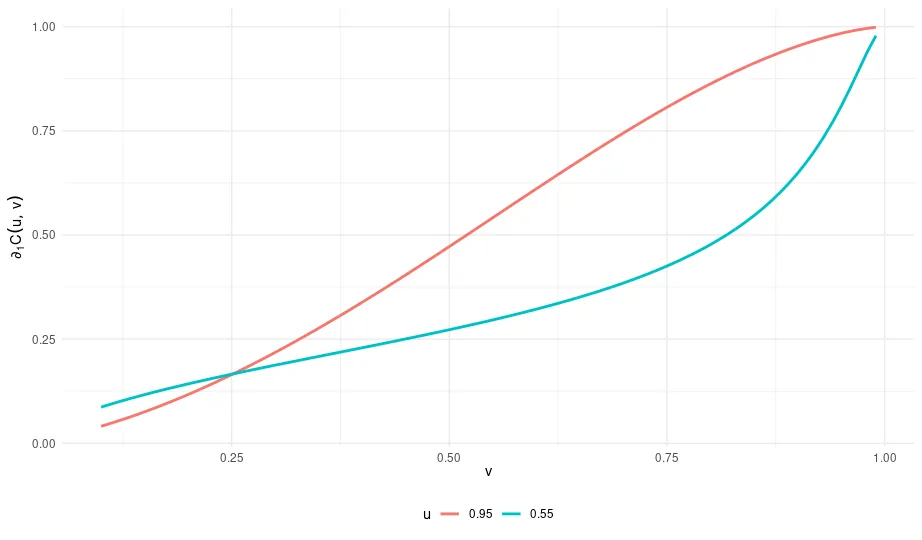
We extend the "probability-equivalent level of VaR and CoVaR" (PELCoV) methodology to accommodate bivariate risks modeled by a Student-t copula, relaxing the strong dependence assumptions of earlier approaches and enhancing the framework's ability to capture tail dependence and asymmetric co-movements. While the theoretical results are developed in a static setting, we implement them dynamically to track evolving risk spillovers over time. We illustrate the practical relevance of our approach through an application to the foreign exchange market, monitoring the USD/GBP exchange rate with the USD/EUR series as an auxiliary early warning indicator over the period 1999-2024. Our results highlight the potential of the extended PELCoV framework to detect early signs of risk underestimation during periods of financial stress.
 2509.12558
2509.12558In this paper, we provide a new property of value at risk (VaR), which is a standard risk measure that is widely used in quantitative financial risk management. We show that the subadditivity of VaR for given loss random variables holds for any confidence level if and only if those are comonotonic. This result also gives a new equivalent condition for the comonotonicity of random vectors.
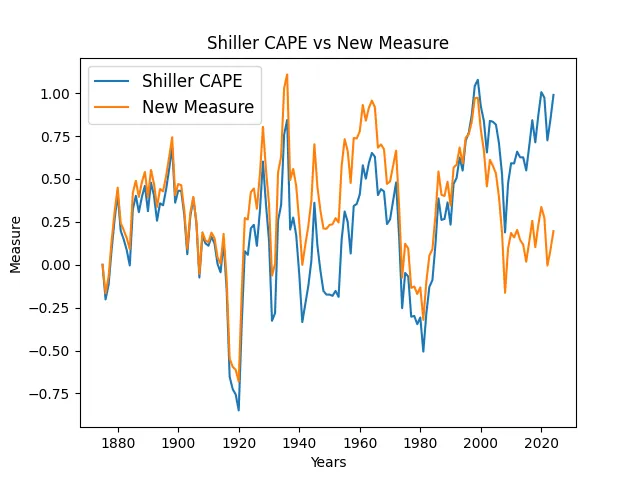
We create a time series model for annual returns of three asset classes: the USA Standard & Poor (S&P) stock index, the international stock index, and the USA Bank of America investment-grade corporate bond index. Using this, we made an online financial app simulating wealth process. This includes options for regular withdrawals and contributions. Four factors are: S&P volatility and earnings, corporate BAA rate, and long-short Treasury bond spread. Our valuation measure is an improvement of Shiller's cyclically adjusted price-earnings ratio. We use classic linear regression models, and make residuals white noise by dividing by annual volatility. We use multivariate kernel density estimation for residuals. We state and prove long-term stability results.
Systemic risk measures aggregate the risks from multiple financial institutions to find system-wide capital requirements. Though much attention has been given to assessing the level of systemic risk, less has been given to allocating that risk to the constituent institutions. Within this work, we propose a Nash allocation rule that is inspired by game theory. Intuitively, to construct these capital allocations, the banks compete in a game to reduce their own capital requirements while, simultaneously, maintaining system-level acceptability. We provide sufficient conditions for the existence and uniqueness of Nash allocation rules, and apply our results to the prominent structures used for systemic risk measures in the literature. We demonstrate the efficacy of Nash allocations with numerical case studies using the Eisenberg-Noe aggregation mechanism.
Measuring the contribution of a bank or an insurance company to overall systemic risk is a key concern, particularly in the aftermath of the 2007--2009 financial crisis and the 2020 downturn. In this paper, we derive worst-case and best-case bounds for the marginal expected shortfall (MES) -- a key measure of systemic risk contribution -- under the assumption that individual firms' risk distributions are known but their dependence structure is not. We further derive tighter MES bounds when partial information on companies' risk exposures, and thus their dependence, is available. To represent this partial information, we employ three standard factor models: additive, minimum-based, and multiplicative background risk models. Additionally, we propose an alternative set of improved MES bounds based on a linear relationship between firm-specific and market-wide risks, consistent with the Capital Asset Pricing Model in finance and the Weighted Insurance Pricing Model in insurance. Finally, empirical analyses demonstrate the practical relevance of the theoretical bounds for industry practitioners and policymakers.
 2411.10139
2411.10139The basic principle of any version of insurance is the paradigm that exchanging risk by sharing it in a pool is beneficial for the participants. In case of independent risks with a finite mean this is the case for risk averse decision makers. The situation may be very different in case of infinite mean models. In that case it is known that risk sharing may have a negative effect, which is sometimes called the nondiversification trap. This phenomenon is well known for infinite mean stable distributions. In a series of recent papers similar results for infinite mean Pareto and Fréchet distributions have been obtained. We further investigate this property by showing that many of these results can be obtained as special cases of a simple result demonstrating that this holds for any distribution that is more skewed than a Cauchy distribution. We also relate this to the situation of deadly catastrophic risks, where we assume a positive probability for an infinite value. That case gives a very simple intuition why this phenomenon can occur for such catastrophic risks. We also mention several open problems and conjectures in this context.
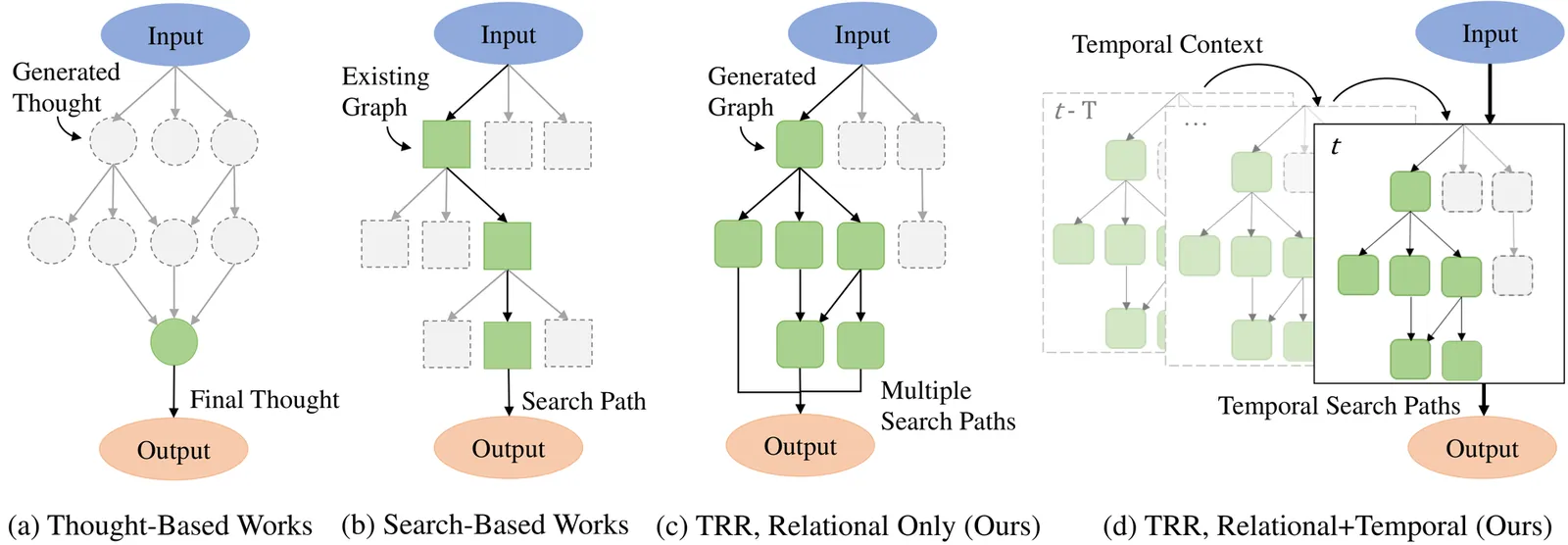
Stock portfolios are often exposed to rare consequential events (e.g., 2007 global financial crisis, 2020 COVID-19 stock market crash), as they do not have enough historical information to learn from. Large Language Models (LLMs) now present a possible tool to tackle this problem, as they can generalize across their large corpus of training data and perform zero-shot reasoning on new events, allowing them to detect possible portfolio crash events without requiring specific training data. However, detecting portfolio crashes is a complex problem that requires more than reasoning abilities. Investors need to dynamically process the impact of each new piece of information found in news articles, analyze the relational network of impacts across different events and portfolio stocks, as well as understand the temporal context between impacts across time-steps, in order to obtain the aggregated impact on the target portfolio. In this work, we propose an algorithmic framework named Temporal Relational Reasoning (TRR). It seeks to emulate the spectrum of human cognitive capabilities used for complex problem-solving, which include brainstorming, memory, attention and reasoning. Through extensive experiments, we show that TRR is able to outperform state-of-the-art techniques on detecting stock portfolio crashes, and demonstrate how each of the proposed components help to contribute to its performance through an ablation study. Additionally, we further explore the possible applications of TRR by extending it to other related complex problems, such as the detection of possible global crisis events in Macroeconomics.